3. Частотные характеристики систем автоматического управления. ч. 3.3 Апериодическое звено 1–го порядка

Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!

3.3. Апериодическое звено 1–го порядка (инерционное звено)

Вывод свойств(характеристик) апериодического звена сделаем на примере фрагмента (части) ядерного реактора, а именно – входной камеры смешения.

Рисунок 3.3.1 Расчетная схема камеры смешения

Сделаем следующие допущения:

расход теплоносителя постоянен: G = const;
теплоемкость теплоносителя = const;
входящий в камеру смешения теплоноситель полностью перемешивается в камере смешения, т.е. температура жидкости, поступающей в каждый тепловыделяющий канал, одинакова;
теплообмен камеры смешения с окружающей средой пренебрежимо мал.

Уравнение теплового баланса:

$\rho \cdot C_p \cdot V \cdot \frac{dT(t)}{dt} = G \cdot C_p \cdot \left[T_{ВХ}(t) -T_{ВЫХ}(t) \right] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.3.1)}$

где: $\rho$ - плотность теплоносителя, кг/м^3
C_p – удельная теплоемкость, $Дж/(кг \cdot K)$
– объем камеры смешения, м^3 ;
– расход теплоносителя, кг/с ;
$T_{ВХ}(t), T_{ВЫХ}(t)$ – температура теплоносителя на входе и выходе, соответственно;
T(t) – температура (перемешанного) теплоносителя в камере смешения $T(t) ≡ T_{ВЫХ}(t)$ .

Условие стационара когда левая часть уравнения равна нулю:

$\frac{dT(t)}{dt} =0 \Rightarrow T_{ВХ}=T_{ВЫХ} =T_0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.3.2)}$

Введем новые переменные:

$\tilde{T}_{ВХ} = \frac{T_{ВХ}(t)-{T}_{ВЫХ}(0)}{{T}_{ВХ}(0)}=\frac{T_{ВХ}(t)-T_0}{T_0}; \Rightarrow T_{ВХ}(t)= T_0 \left[1+ \tilde{T}_{ВХ}\right];\\ \tilde{T}=\tilde{T}_{ВЫХ} = \frac{T_{ВЫХ}(t)-{T}_{0}}{{T}_{0}}; \Rightarrow T_{ВЫХ}(t)= T_0 \left[1+ \tilde{T}_{ВЫХ}\right]=T(t);$

Подставляя эти соотношения в (3.3.1), получаем:

$\rho \cdot C_p \cdot V \cdot T_0 \cdot \frac{d\tilde{T} }{dt} = G \cdot C_P \left[ T_0+T_0 \cdot \tilde{T}_{ВХ}(t) - T_0 - T_0 \cdot \tilde{T}(t)\right] = \\ =G \cdot C_P \cdot T_0 \left[ \tilde{T}_{ВХ} - \tilde{T}(t)\right];$

Сокращая на T_0 и C_p , получаем:

$\rho \cdot V \cdot \frac{d\tilde{T} }{dt} = G \cdot \left[ \tilde{T}_{ВХ}(t) - \tilde{T}(t)\right] \Rightarrow \\ \frac{\rho \cdot V}{G} \cdot \frac{d\tilde{T} }{dt}+ \tilde{T}(t) = \tilde{T}_{ВХ}(t)$

Введем новую переменную $\tau$ - постоянная времени:

$\tau = \frac{\rho \cdot V}{G}$ $\tau \cdot \frac{d\tilde{T}(t)}{dt} +\tilde{T}(t) = \tilde{T}_{ВХ}(t) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.3.3)}$

Таким образом получили линейное дифференциальное уравнение, причем переменные ${T}_{ВХ}(t)$ и $\tilde{T}(t)$ - нормализованные, что обеспечивает равенство их нулю при t ≤ 0

$\tau$ – постоянная времени;
$\frac{d\tilde{T}(t)}{dt}$ – аналог y’(t);
$\tilde{T}(t)$ – аналог y(t);
$\tilde{T}_{ВХ}(t)$ – аналог x(t);

Уравнение (3.3.3) соответствует типовому апериодическому звену 1-го порядка, в котором коэффициент K = 1. В общем случае уравнение динамики апериодического звена 1-го порядка имеет вид:

$T \cdot y'(t)+y(t) = K \cdot x(t) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.3.4)}$

Если начальные условия нулевые, то можно перевести в изображения:

$y(t) \rightarrow Y(s) \\ y'(t) \rightarrow s \cdot Y(s) \\ x(t) \rightarrow X(s)$

Уравнение динамики в изображениях:

$[ T \cdot s +1 ] \cdot Y(s) = K \cdot X(s) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.3.5)}$

Уравнение динамики в изображениях:

$W(s) = \frac{Y(s)}{X(s)} = \frac{K}{T \cdot s+1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.3.6)}$

Найдем выражение для АФЧХ:

$s = i \cdot \omega \Rightarrow W(i \cdot \omega) = W(s)\mid_{s = i \cdot w} = \frac{K}{T \cdot i \cdot \omega+1} \ \ \ \ \ \ \mathbf{(3.3.7)}$

Умножим на комплексно – сопряженное значение $(1 - i \cdot T \cdot \omega)$ :

$W(i \cdot \omega) =\frac{K \cdot(1- i\cdot T \cdot \omega)} {(1+ i \cdot T \cdot \omega)(1 - i \cdot T \cdot \omega)} = \underbrace {\frac{K}{1+T^2 \cdot \omega^2}}_{Re =u(\omega)} - i \cdot \underbrace {\frac{K\cdot T \cdot \omega}{1+T^2 \cdot \omega^2}}_{Im =v(\omega)}\Rightarrow$ $u(\omega) = \frac{K}{1+T^2 \cdot \omega ^2} \ \ \ \ \ \mathbf{(3.3.8.a)}\\ v(\omega)= -\frac{K \cdot T \cdot \omega}{1+ T^2 \cdot \omega^2}\ \ \ \ \ \mathbf{(3.3.8.b)}$

Анализируя поведение u(ω) и v(ω) при $\omega \rightarrow 0$ и при $\omega \rightarrow \infty$ , получаем:

$\omega \rightarrow 0 \Rightarrow \left \{ \begin{gathered} u(\omega) \rightarrow K \\ v(\omega) \rightarrow 0\ \end{gathered} \right.$ $\omega \rightarrow \infty \Rightarrow \left \{ \begin{gathered} u(\omega) \rightarrow 0 \\ v(\omega) \rightarrow 0\ \end{gathered} \right.$

Подставляя в формулы (3.3.8) различные значения частоты ω, найдем соответствующие значения u(ω) и v(ω). Построим эти вектора на комплексной плоскости:

Рисунок 3.3.2 – Годограф АФЧХ апериодического звена 1-го порядка

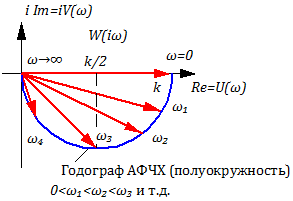
Анализ показывает, что годограф АФЧХ — полукруг радиусом K/2. Формулы для дейстивительной части вектора $u(\omega)$ и мнимой части вектора $v(\omega)$ , позволяют вычислить частоту, на которой вектор находится в нижней точке окружности $\omega_3$ (см. рис. 3.3.2).

$\omega_3 = \frac{1}{T} \Rightarrow \left \{ \begin{gathered} u(\omega_3) = \frac{K}{2} \\ v(\omega_3) = - \frac{K}{2} \ \end{gathered} \right.$

Угол сдвига фазы при данной частоте: $\phi_3 = \phi(\omega_3)=\frac{\pi}{2}$

Найдем зависимость амплитуды от частоты:

$A(\omega) = \sqrt{ \left( \frac{K}{1+T^2 \cdot \omega^2} \right)^2+\left( \frac{K\cdot T \cdot \omega}{1+T^2 \cdot \omega^2} \right)^2} = \frac{K}{\sqrt{1+T^2\cdot \omega^2}}\ \ \ \ \mathbf{(3.3.9)}$

Учитывая, что годограф АФЧХ находится в IV-ой квадранте:

$\phi(\omega)= - arctg \frac{v(\omega)}{u(\omega)} =-arctg\frac{K \cdot T\cdot \omega \cdot(1+T^2\cdot \omega^2)}{K \cdot(1+T^2 \cdot \omega^2)} \Rightarrow\\\phi(\omega) =-arctg(T \cdot\omega) \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(3.3.10)}$

Рисунок 3.3.3 – АЧХ апериодического звена 1-го порядка

Рисунок 3.3.4 – ФЧХ апериодического звена 1-го порядка

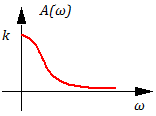
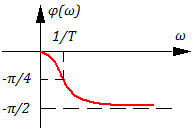
Логарифмическая амплитудная характеристика (ЛАХ) и фазочастотная характеристика (ФЧХ).

$Lm(\omega) = 20\cdot lg (A(\omega))=20 \cdot lg \frac{K}{\sqrt{1+T^2\cdot \omega^2}} \Rightarrow \\Lm(\omega)=20\cdot lg(K) - 20 \cdot lg \sqrt{1+T^2 \cdot \omega^2} \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{3.3.11}$

Рисунок 3.3.5 ЛАХ и ЛФЧХ апериодического звена 1-го порядка

Анализируя частотные свойства данного звена, видим, что

при ω << $\frac{1}{T}$ свойства звена приблизительно совпадают со свойствами идеального усилительного звена, т.е. $W(i\cdot \omega) \ \approx K \Rightarrow W(s) \approx K$ ≈ K => W(s) ≈K.
при ω >> $\frac{1}{T}$ свойства звена приблизительно совпадают со свойствами идеального интегрирующего звена, т.е. $W(i\cdot \omega) \ \approx \frac{K}{i \cdot \omega \cdot T} \Rightarrow W(s) \approx \frac{K}{T \cdot s}$ .
при ω $\approx \frac{1}{T}$ на свойства звена оказывают примерно равное “влияние” свойства идеального усилительного и идеального интегрирующего звена.

Принято называть частоту, при которой происходит “излом” ЛАХ

$\omega_{сопр} = \frac{1}{T}$ − сопрягающей частотой,

причем не трудно показать, что при ω_сопр величина амплитуды А(ω_сопр) меньше амплитуды при нулевой частоте A(0) = K в $\sqrt{2}$ раз:

$A(\omega_{сопр}) = \frac{K}{\sqrt{2}}$

Частотой среза ω_срназывают такое значение частоты, при которой модуль (амплитуда) выходного сигнала (воздействия) равна 1.

$A(\omega_{ср})=\frac{K}{\sqrt{1+T^2 \cdot \omega_{ср} ^2}}=1 \Rightarrow\\ \omega_{ср} =\frac{\sqrt{K^2-1}}{T}$

Если K>>1 , то частота среза $\omega_{ср} = \frac{K}{T}$

Если , то частоты среза не существует !

Найдем переходную функцию звена (реакция на единичное ступенчатое воздействие):

$h(t) = L^{-1} \left[ H(s)\right] = L^{-1} \left[ \frac{ W(s)}{h}\right] = L^{-1} \left[ \frac{K}{s \cdot (T\cdot s+1)}\right]$

Используя обратное преобразования Лапласа (см. пример в разделе 2) получим:

$h(t) = K \cdot \left[ 1- e^{-\frac{t}{T}}\right]$

Тогда, дифференцируя по времени, получаем весовую функцию ω(t):

$w(t) = \frac{K}{T} \cdot e^{-t/T} \cdot1(t)$

Множитель 1(t) обеспечивает равенство нулю при t ≤ 0

Рис.3.3.6 Переходная функция апериодического звена 1-го порядка

Рис.3.3.7 Весовая функция апериодического звена 1-го порядка

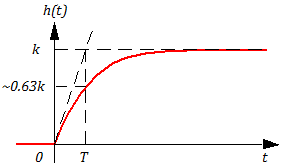
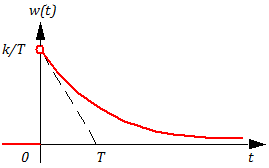
Постоянная времени Т характеризует инерционность переходных процессов в звене. Чем больше Т, тем инерционнее звено (т.е. медленнее идет переходной процесс).

Примерами апериодического звена 1- го порядка являются:

1) пассивные R−L или R−C цепочки (см. рисунок 3.3.8);

Рисунок 3.3.8 Примеры апериодических звеньев 1-го порядка

2) упрощенная модель гидротурбины, где x(t) - приводной момент; y(t) − скорость вращения ротора турбины;

3) электродвигатель (постоянного тока или асинхронный) с учетом инерционности якоря (ротора), где x(t) − напряжение в обмотке возбуждения, а y(t)− скорость вращения якоря (ротора) выходного вала;

4) тепловые датчики, например, термопара, где: x(t) –температура одного (“горячего”) спая, а y(t) – термо Э.Д.С.

5) выходная камера смешения в реакторе (приближенно)

6) различные элементы реактора, описываемые в рамках точеных моделей (например, активная зона или ядерное горючее) с использованием закона Фурье:

$c \frac{dT(t)}{dt} = N_{out}(t)-\alpha_{v}[T(t)-T_*]$

где: T(t) − температура топлива;

$\alpha_v$ − “объемный” коэффициент теплоотдачи;

$N_{out}$ − выделяющаяся энергия;

T_* − температура кипения теплоносителя.

Пример

Лично мне всегда было интересно, насколько теория совпадает с практикой, особенно для элемента ядерного реактора. Идеальный вариант – это разобрать туалетный бачок и сделать из него модель реактора, но, боюсь, домашние не одобрят, поэтому сравнивать будем с «цифровым двойником».

Рассмотрим расчет характеристик камеры смешения, в которую подается вода при температуре 20 °С и атмосферном давлении.

В качестве единичного воздействия будем считать изменение температуры на 1 °C.

Свойства воды при 20 градусах и атмосферном давлении:

теплоёмкость: = 4183 $\frac{Дж}{кг \cdot град}$ ;
плотность: $\rho$ = 998.2 $\frac{кг}{м^3}$ .

Параметры системы:

объем камеры смешения: V = 0.1 ;
массовый расход воды: G = 50 $\frac{кг}{с}$ .

Решим задачу в двух приближениях:

В первом случае используем стандартный блок «Инерционное звено первого порядка», который есть в любой системе структурного моделирования, и модель общего вида.
Во втором воспользуемся расчетным тепло-гидравлическим кодом НS, который используется для создания профессиональных моделей в атомной отрасли.

Параметры блока «Инерционное звено первого порядка» задаем с помощью скриптового языка при инициализации проекта, где рассчитывается постоянная времени. (см. рис. 3.3.9). В качестве входного воздействия задаем ступеньку на пятой секунде расчета величиной 0.05, что соответствует повышению на 1 °C от начальных 20 °C .

На схеме присутствует также блок «Построение частотных характеристик», обеспечивающий расчет ЛАХ и ФЧХ в заданном диапазоне 0.1 – 1000 1/с.

Расчетная схема и результаты расчета приведены на рисунке 3.3.9:

Рисунок 3.3.9 Частотный анализ модели камеры смешения в виде стандартного апериодического звена

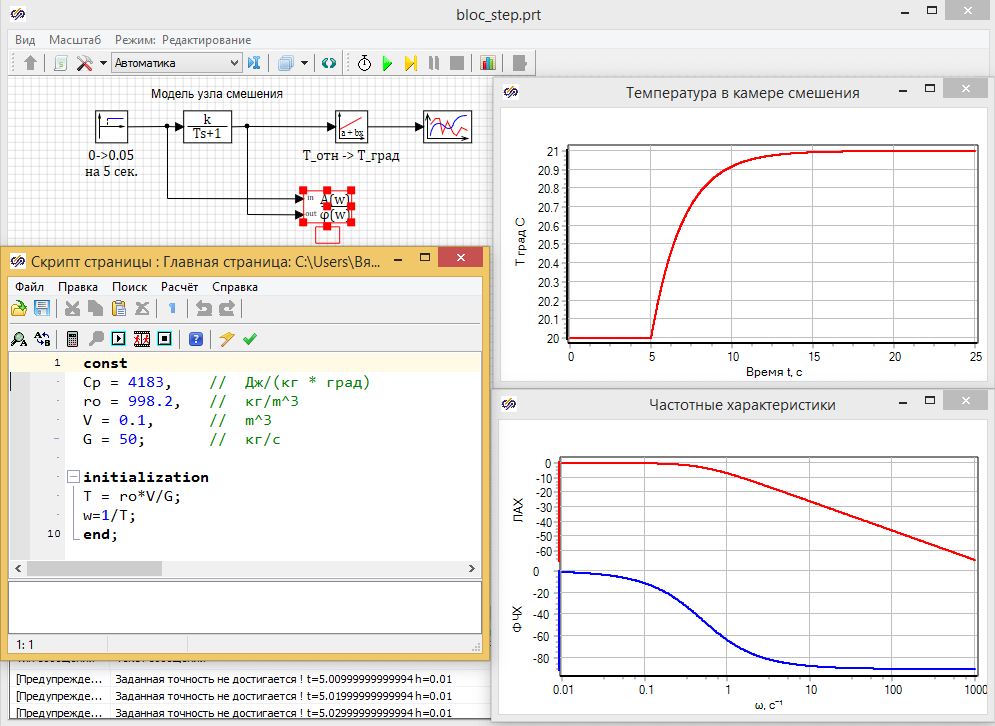
Видно, что расчетные характеристики в модели совпадают с теоретическими:

1) Постоянная времени T = 1.996

2) Сопрягающая частота w_сп = 1/T = 0,5009

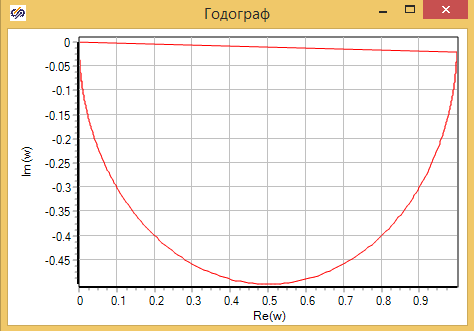
Годограф звена, построенный с помощью Гармонического анализатора, представлен на рисунке 3.3.10, Видно, что получена полуокружность с центром в точке (0, 0.5) и диаметром К = 1, как и предсказано в теоретической части.

Рисунок 3.3.10 Годограф модели камеры смешения в виде «Инерционного звена первого порядка».

Второй вариант модели в камере смешения моделируется с помощью тепло-гидравлического расчетного кода - НS. Данный код входит в состав «Среды динамического моделирования технических систем SimTech». В коде решается более подробная система уравнений теплофизики, описание можно посмотреть здесь. Модель камеры смешения будет состоять из 4 элементов:

Блок «Подпитка» обеспечивает подачу теплоносителя с заданными параметрами и заданным расходом. В нашем случае это вода при атмосферном давлении и температурой 20 °C.
Блок «Внутренний узел» (Node_1), - модель камеры смешения.
Блок «Канал общего вида» моделирует обобщенно каналы отвода теплоносителя от камеры смешения (состоит из 10 участков).
Блок «Граничный узел» задает температуру и давление на выходе из каналов. В нашем случае – атмосферное давление и температуру.

Общий вид модели приведен на рисунке 3.3.11 Цветовая шкала показывает распределение давления в канале, который идет после камеры смешения. Исходя из уравнений физики, система рассчитывает перепад давления, соответствующий заданному расходу по каналу (50 кг/с) с учетом его геометрии, свойств жидкости, шероховатости и т.п.

Рисунок 3.3.11 Модель камеры смешения в коде НS.

Если вывести график температуры в узле, то можно увидеть, что в начальный момент расчёта происходит какой-то переходной процесс, несмотря на то что никакого внешнего воздействие на систему нет (см. рис. 3.3.12).

Рисунок 3.3.12 Температура в узле в начальный период расчета.

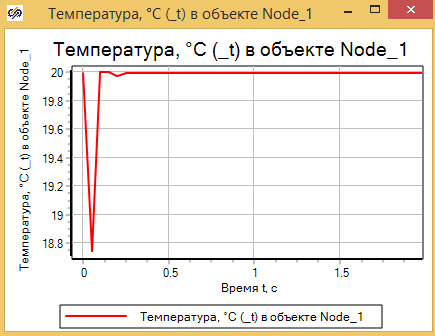
Все дело в том, что система у нас динамическая, и распределение расхода и температур по узлам модели в начале расчёта не соответствует стационарному состоянию. И некоторое время происходят колебания расходов и, соответственно, температур до достижения равновесия.

Чтобы в расчётах не учитывать данные колебания, и не заставлять пользователя задавать вручную состояние каждой точки системы, используется специальный инструмент «Файл рестарта». В этот файл сохраняются состояния системы в конце расчета или с заданным шагом. И эти состояния можно загрузить при старте системы. Если сохранить состояние системы, находящейся в стационаре один раз, то потом можно использовать его для начала расчёта, тем самым избегая колебаний системы. Для этого необходимо:

В настройках проекта задать имя файла, в который мы хотим сохранить стационарное состояние в конце расчета.
В следующих расчетах указать этот файл как начальное состояние при старте нового расчета, и изменить в нем модельное время на 0 (см. рис. 3.3.13).
Не забываем снять галочку «Сохранять рестарт при останове», если мы не хотим каждый раз получать новое состояние после каждого расчета.

Рисунок 3.3.13 Настройка файлов рестартов.

Теперь если загрузить систему из файла рестарта, созданного в стационарном состоянии, то колебания температуры на начальном этапе исчезнут. И можно проводить эксперименты с воздействием.

Для того, чтобы сравнить модель в виде динамического звена и модель в тепло-гидравлическом коде, сделаем пакет из двух проектов:

гидравлическая модель в коде НS;
модель виде одного звена.

Обмен данными будет идти через базу данных сигналов. Передадим результаты расчета из гидравлического кода в модель с одним звеном и выполним сравнение результатов. Вид пакета представлен на рисунке 6.

В главном скрипте гидравлической схемы пропишем переменную T_input – температуру на входе в камеру, на 5 секунде расчёта увеличим эту температуру на °C. А температуру в узле будем записывать в базу данных сигналов в категорию nodе_HS, переменная T_out.

В модели общего вида прочитаем значение сигнала в базе данных nodе_HS_T_out.

Сравним с выходом из апериодического звена (модель камеры смешения) и выведем на один график.

Рисунок 3.3.13 Пакет для сравнения моделей узла смешения.

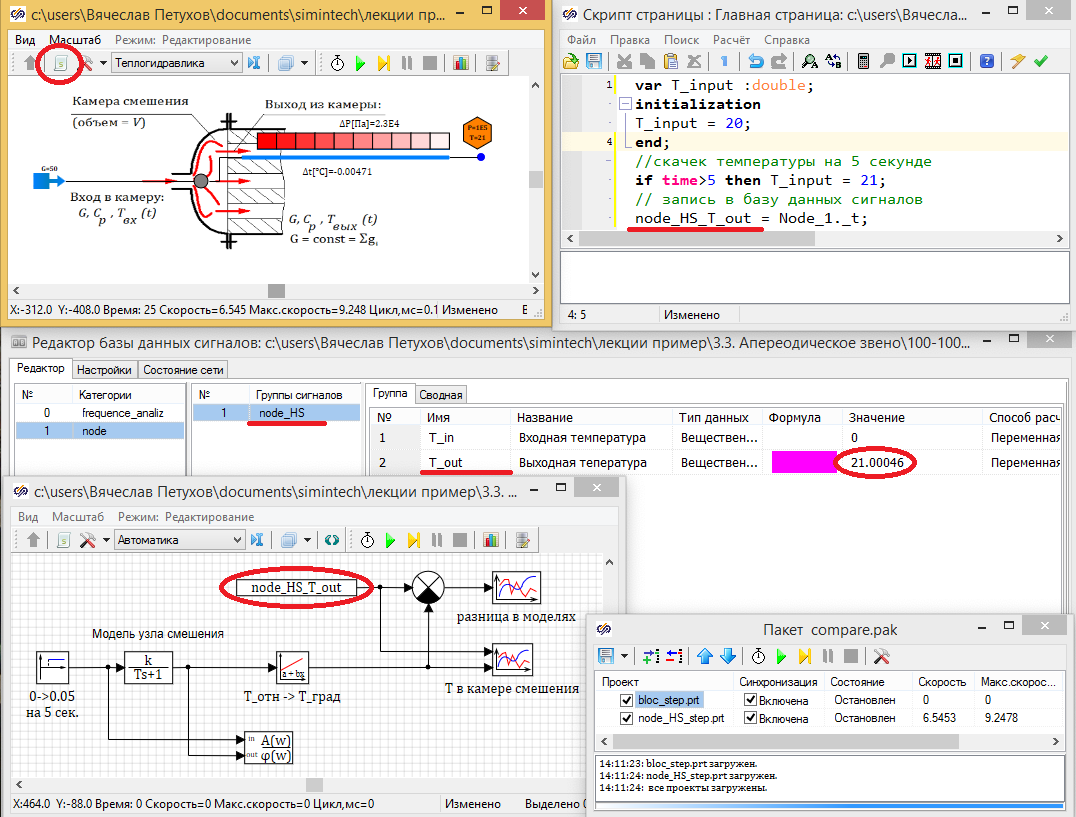
Результаты совместного расчета представлены на рисунке 3.3.14

Если на общем графике в масштабе 20 – 21 °C графики практически совпадают, то анализ графика сравнения показывает наличие расхождения в момент ступенчатого изменения температуры. Причем максимальное расхождение 0.0085 °C отмечено именно в момент переключения, а потом происходит выравнивание температуры (см. рис. 3.3.14).

Рисунок 3.3.14 Сравнение переходного процесса для разных моделей камеры смешения.

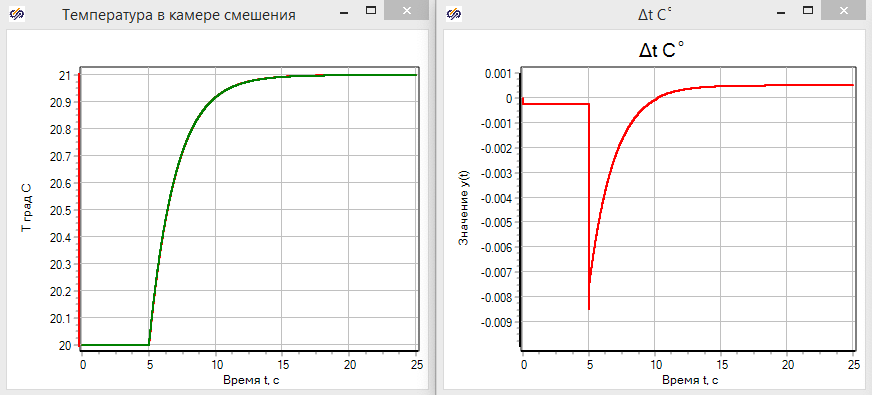
Разница связанна как раз с более сложной и детализированной моделью в тепло-гидравлическом коде НS. Дело в том, что в реальности и плотность и теплоёмкость воды не являются постоянными, а зависят от параметров давления и температуры, и даже изменение температуры на один градус ведет к изменению подведения.

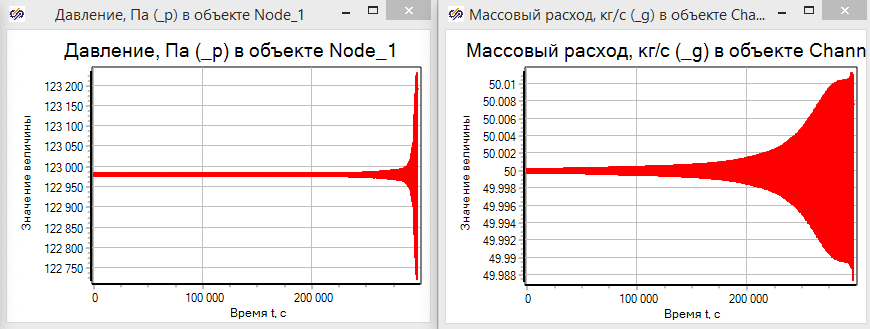
Если в масштабе посмотреть на поведение давления в камере смешения и расхода из нее, мы увидим, что несмотря на то, что расход в камеру задавался постоянным, увеличение температуры скачком привело к возникновению колебательного процесса в давлении и массовом расходе из камеры (см. рис. 3.3.15).

Рисунок 3.3.15 Колебания давления и расхода при ступенчатом изменении температуры.

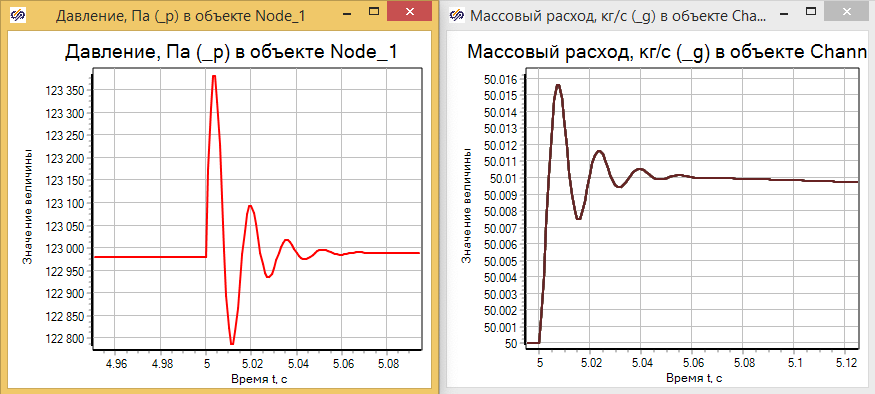
Колебания незначительны по времени и по амплитуде, но тем не менее они влияют на расчетный процесс и хорошо наблюдаемы при масштабировании графиков.

Проведем исследования с помощью блока "Гармонический анализатор". Создадим пакет проектов, состоящий из:

тепло-гидравлической модели (см. рис. 3.3.11);
модели частотного анализа. (см. рис. 3.3.16).

Рисунок 3.3.16 Модель частотного анализа внешней системы.

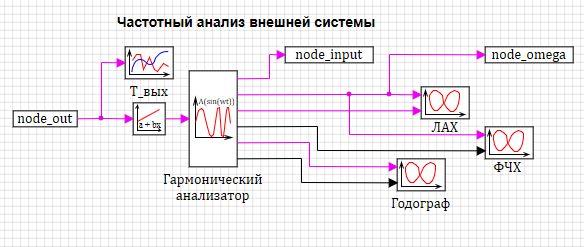
В предыдущей лекции у нас блок гармонического анализа и анализируемая модель были в одном проекте. В данном проекте блок гармонического анализа передает воздействие в базу сигналов и забирает из нее отклик – температуру в камере смешения.

Особенностью данной модели является то, что в начале расчёта на низких частотах нам нужен большой шаг интегрирования, чтобы считать медленный процессы быстрее. В начале анализа у нас частота 0.001 Гц.

А в конце процесса частота 1000 Гц, и нам нужно сократить шаг интегрирования, чтобы получить достаточное количество точек в синусоидальном сигнале при высокой частоте.

Поэтому в базу данных записывается не только тестовое воздействие, но и текущая частота (см. рис. 3.3.17). Это позволяет при увеличении частоты воздействия уменьшить минимальный шаг расчета тепло-гидравлической схемы. Скрипт модели приведен на рисунке 3.3.17.

Рисунок 3.3.17 Скрипт гидравлической модели.

Как работает этот скрипт?

Начальное значение температуры 20 °C.

Если частота воздействия больше 100, то минимальный шаг модели 0.00001, иначе (при частоте воздействия меньше 100) минимальный шаг модели 0.0001.

Температура в блоке подпитки T_input рассчитывается как сумма начальной температуры 20°C и величины воздействия node_input из базы данных сигналов, которое формирует блок гармонического анализатора в диапазоне -1 … +1 °C.

Температура в узле передаётся в базу данных для гармонического анализатора.

Результат длительного расчёта представлен на рисунке 3.3.18.

Рисунок 3.3.18. Результаты анализа частотного анализа гидравлической модели.

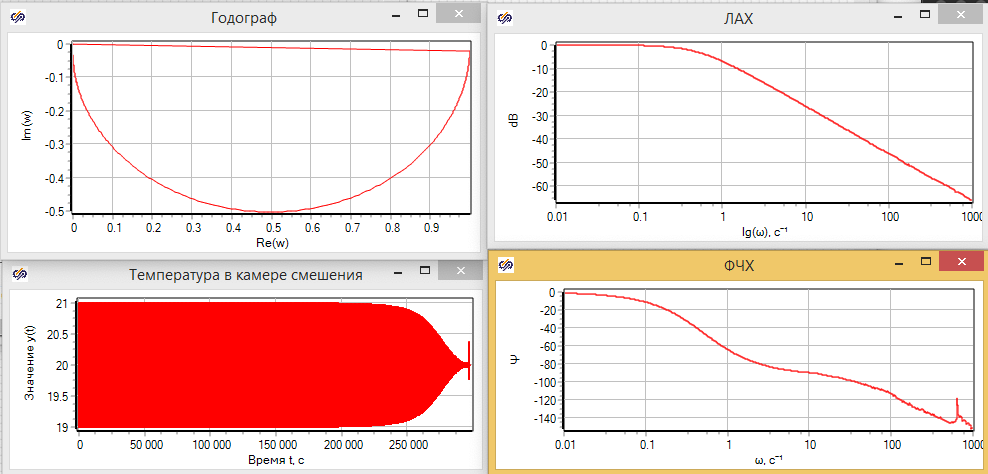
Мы видим, что несмотря на различия в математических моделях, частотные характеристики камеры смешения в тепло-гидравлическом коде отлично совпадают в диапазоне частот 0.001 до 50 Гц. Сравни с рисунком 3.3.9

Однако на частотах выше 70 ФЧХ ведет себя не так, как в идеальном апериодическом звене. Если открыть график давления в камере смешения и график массового расхода в канале, можно наблюдать увеличение амплитуды колебаний с ростом частоты воздействия (см. рис. 3.3.19).

Рисунок 3.3.19 Давление в узле и расход в выходном канале с ростом частоты воздействия по температуре.

Таким образом изначальная модель, в которой можно было пренебречь колебаниями давления и массового расхода, с ростом частоты воздействий выше 50 Гц превращается в модель, где принятые допущения уже не работают.

Выводы.

Теория автоматического управления действительно работает, и даже ядерный реактор можно представить в виде набора динамических звеньев.

Однако нужно внимательно смотреть за параметрами процессов, и определять диапазоны, где принятые упрощения настолько изменяют систему, что делают модель не верной .

Примеры моделей из лекции для самостоятельного изучения.

Предыдущая лекция.

Ссылки по теме моделирования систем:

Цифровой двойник системы кондиционирования воздуха (СКВ) самолета
Модельно ориентированное проектирование. Создание достоверной модели, на примере авиационного теплообменника
Конечные автоматы в среде динамического моделирования SimInTech
Модельно-ориентированное проектирование. Построение активного выпрямителя (на основе математической модели)
«Технология» получения уравнений динамики ТАУ. И почему System Identification is sucks, а рулит «честная физика»
Модельно ориентированное проектирование. Электропривод с бесколлекторным двигателем постоянного тока
Ведение в моделирование динамики квадро-, гекса- и октокоптеров

Источник: https://habr.com/ru/post/536636/

Вернуться к списку

Интересные статьи

Концепция Облачной операционной системы

Привет Хабр! Меня зовут Ильдар. Хочу поделиться с сообществом своими идеями разработки Облачной ОС. Начну с рассказа простого кейса, почему я начал задумываться о создании Облачной ОС. В...

Пишем бизнес-процесс в Битрикс24 с задатком на будущее

На работе я занимаюсь поддержкой пользователей и обслуживанием коробочной версии CRM Битрикс24, в том числе и написанием бизнес-процессов. Нужно отметить, что на самом деле я не «чист...

«Спасите Конкорд» или репортаж с испытаний российской радиолокационной системы поиска посторонних предметов на ВПП

Это фото скромного аэродрома «Орловка» (код ИКАО: UUTO) в Тверской области — на самом деле очень символично. Впервые в истории Россия присоединяется к клубу технологических лидеров, способных...

Astra Linux 1.6 (Смоленск). Готова ли система к работе с простыми пользователями? Примеры костылей

Нейтрализация пользователя и процесс установки новой ОС Привет, Хабр. Сегодня хотим поделиться опытом миграции одной организации (далее – Заказчик) на отечественную ОС в рамках выполнения тр...

Система частиц в Core Animation. Рождественская история

Всем привет! Рождество давно прошло, но после него у нас осталась занимательная история о том, как при помощи нечасто используемой возможности Core Animation можно создать пользователям пр...