Предисловие
Притяжение властвует на больших расстояниях, оно универсально и очевидно в сравнении с другими взаимодействиями, но нюанс заключается в том, что оно невероятно слабо — в 1039 раз слабее электромагнитного взаимодействия, а ее влияние на микроскопическом уровне вовсе незаметно. Природа гравитации в мире элементарных частиц ломает умы ученых не один десяток лет, ведь она не хочет мириться ни с квантовой физикой, ни с электродинамикой. Струнная теория так же не может удовлетворить конфликт гравитации с другими взаимодействиями. Но, кажется, мы нашли способ помирить гравитацию с физикой. Как? Предположить, что она — не фундаментальное взаимодействие.

Любой вопрос или замечания Вы можете написать в комментариях. Также я открыт для личного диалога в телеграме или даже беседы в нашем чате. А еще у меня есть телеграм-канал о космологии.
Информация и ее роль во Вселенной
Рассматривая гравитацию во вселенной с инвариантными процессами с точки зрения струнной теории, исследователи пришли к выводу, что гравитация истекает из законов микроскопических взаимодействий и свойства информации. Информация играет важнейшую роль в устройстве Вселенной и понимание ее содержания поможет нам создать точную описательную модель нашего мира. Информация отражает абсолютно все: начиная от состава материи или энергии до его положения. Мера содержания информации характеризуется т.н. энтропией, которая оказывается для нас чрезвычайно полезной, когда речь заходит о выборе объективной меры количества информации.
Попробуем рассмотреть данное предложение в двоичном коде — тогда его энтропией будет то количество знаков, которое необходимо для его кодирования и количество их возможных состояний (0 или 1), называемых степенью свободы. По поводу понимания сущности энтропии у меня есть интересная статья, рекомендую к прочтению.
Энтропия черных дыр и интересные выводы об этом
А если вместо предложения у нас будет черная дыра? На мой взгляд, это самый простой и самый сложный для понимания объект одновременно. Многие ошибочно считают, что информация о поглощенном черной дырой теле неизбежно в нем исчезает, а также что единственное известное свойство черной дыры — это количество энергии в ней. Благо, все устроено иначе — если мы проанализируем взаимодействие черной дыры, то убедимся, что при поглощении объекта от него передается энергия, а также момент импульса, что неизбежно влияет на массу и состояние черной дыры и проще это выражается одним словом — информация. Информация об объекте осталась с информацией черной дыры и отражается в последствиях взаимодействия с поглощенным телом. Ну и если поразмыслить еще, то мы вспомним, что утеря информации несет за собой упорядочивание и уменьшение энтропии, что противоречит второму закону термодинамики, гласящем о том, что энтропия замкнутой системы постоянно не убывает. Об этом впервые высказался американский физик Джон Уиллер.

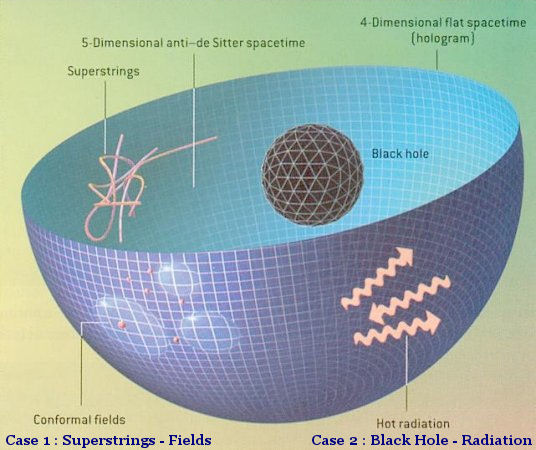
Ага. Эта штука называется голографическим принципом и говорит о том, что любая n-мерная система с i-тым количеством информации экспериментально идентична (n-1)-мерной сфере с тем же количеством информации вне зависимости от того, насколько различны описательные характеристики этих систем. Это в прямом смысле проецирование на экран в кинозале — ведь с помощью двухмерной проекции мы получаем такое же количество информации, что и получал оператор с трехмерной. Черная дыра — тот же оператор. Она сохраняет объективную информацию об объекте на своей двухмерной поверхности нулей и единиц, именуемой горизонтом событий и отражает ее в виде излучения Хокинга. И никакого нарушения принципа энтропии.
А что там с гравитацией?
Как я сказал в самом начале, гравитация тесно связана с информацией, а следовательно, и с энтропией. Хуан Малдасена, струнный теоретик, смог рассмотреть гравитацию через призму голографического принципа, представив модель с n-мерным пространством-временем, где материя подчинена струнному взаимодействию, окруженную (n-1)-мерной сферой, где та самая струнная теория превращалась в квантовую гравитацию. Как? Колебания браны неизбежно приводят к гравитационному взаимодействию на граничащей поверхности. Это была первая попытка показать гравитацию как не первопричину, а следствие какого-то другого фундаментального взаимодействия.
Второй, наиболее успешной попыткой стала статья Эрика Верлинде, вышедшая в 2010 году и взбудоражившая умы СМИ и публики — «О природе тяготения и законов Ньютона». Верлинде на основании энтропийной природы гравитации удалось вывести законы Ньютона и уравнения Эйнштейна. Давайте приступим к основной части этого материала и рассмотрим основные тезисы его работы.

В первую очередь, в своем исследовании Верлинде утверждает, что гравитация — это явление изменения информации о материальных телах, подчиняющееся голографическому принципу. Зададим энергию двух тел, а также их взаимное положение. По второму закону термодинамики энтропия этой системы останется либо постоянной, либо начнет расти. Рост энтропии будет лишь в том случае, если тела начнут сближаться друг со другом, т.к. это вызовет рост степеней свободы системы — в ином случае энтропия будет уменьшаться. Так как энтропия должна расти, тела будут неизбежно вступать во взаимодействие, называемое гравитацией. Это похоже на принцип Гейзенберга и флуктуации частицы — невозможно единомоментно определить положение и состояние частицы, потому, например, поместив на дно сосуда частицу, вместо ожидаемого покоя в минимуме потенциальной энергии мы будем наблюдать ее колебания, называемые также флуктуациями.

Для доказательства этих соображений предлагаю рассмотреть частицу массой m, находящуюся на расстоянии x от голографического экрана площадью S. Частица будет неизбежно приближаться к голографическому экрану и их микроскопические степени свободы сольются. В таком случае формула приращения энтропии будет:
Энтропийная сила — это ни что иное, как причина компенсировать уменьшение энтропии:
где T — температура.
Известно, что сила связана с ускорением, которое также связано и с температурой. Квантовый эффект Унру гласит, что наблюдатель в ускоренной системе отсчета обладает температурой:
где a — ускорение. Из вышеполученных выражений несложным образом получаем математическое представление второго закона Ньютона:
Теперь представим область пространства, заключенную в сферу с энергией E и с голографической поверхностью. Вспомним, что емкость сферы пропорциональна площади ее поверхности. Тогда мы можем выразить число битов системы N как:
Также вспомним самую знаменитую формулу физики (или, как минимум, Эйнштейна):
где m — масса, заключенная в части ограниченного сферическим экраном пространства. Подставив в выражение площадь сферы, равную:
получим:
Удивительно, но мы приходим к неутешительному выводу о том, что гравитацию можно рассматривать как несамостоятельное явление природы, зависящее от энтропии в рамках голографического принципа. Эрик Верлинде в своем исследовании также заметил, что энтропийную природу может иметь и красное смещение, возникающее вследствие градиентов энтропии — специально поэтому я также кратко рассмотрю работу (Easson et al.), рассматривающую темную энергию и ускоренное расширение с точки зрения энтропийной природы гравитации. Последующий пункт будет занят математическими вычислениями, вывод по статье ждет вас в соответствующем разделе. Математика для неподготовленных будет ограничена горизонтальными чертами — после второй можете продолжить чтение.
Для начала вспомним, что такое темная энергия. По Общей теории относительности и космологическому принципу масштабный фактор a(t) в FLRW-метрике удовлетворяет уравнению Фридмана:
где масштабный фактор в настоящий момент равен единице, а ρ — плотность энергии компоненты, ответственной за расширение Вселенной, где для расширяющейся ускоренно Вселенной:
а также
Для значения омеги, равного (-1), получим:
где
Продифференцируем уравнение масштабного фактора по времени и получим:
Подставим полученное в уравнение Фридмана:
где
Предсказанное таким образом значение плотности темной энергии составляет 1018 ГэВ4. Наблюдаемое же значение равно 10-3 эВ4 — отличие на 120 порядков! Во избежание данного казуса авторами статьи было предложено энтропийное истолкование космологической константы. Для этого рассмотрим горизонт голографической поверхности с температурой:
Из ранее упомянутого эффекта Унру следует, что горизонт, обладающий температурой, должен неизбежно ускоряться:
При данном мы можем видеть, как темная энергия становится лишним компонентом — теперь мы можем объяснить космологическое ускорение без нее. Исследователи решили сравнить свои теоретические изыскания с нашей моделью Вселенной на примере сверхновых типа Ia. Для этого они взяли стандартную формулу фотометрического расстояния и построили две кривые:
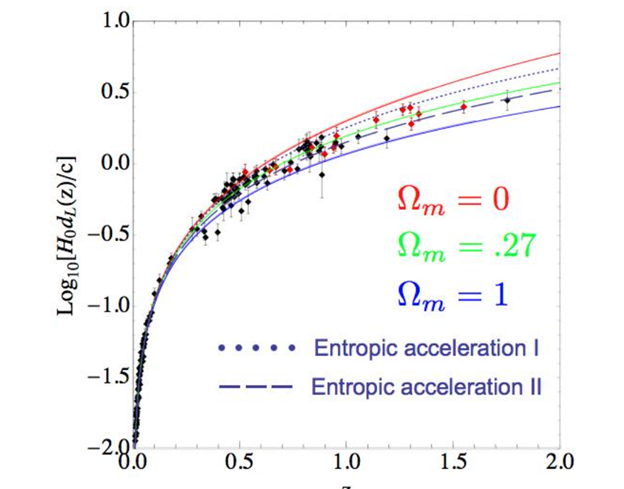
Ускорение, обусловленное энтропийными силами, как оказалось, обеспечивают такой же гладкий переход кривой в горизонтальное положение, что и в уже классической интерпретации светимости сверхновых.
Краткий вывод
На основании проведенных теоретических опытов, можно сделать вывод о том, что:
Энтропийная трактовка гравитации удовлетворяет теоретическим предположениям для модели, соответствующей релятивистской плоской вселенной и ньютоновской вселенной;
Энтропийная трактовка ускоренного расширения вселенной потенциально способно объяснить природу космологического ускорения без привлечения темной энергии.
Сказать, что это круто — ничего не сказать. Мы, вероятно, находимся совсем вблизи от нового научного прорыва, похожего на тот, что совершил Альберт Эйнштейн более ста лет назад. Даже если мы не сможем доказать справедливость голографического принципа для нашей Вселенной, мы откроем для себя новый мир, полный струн — не музыкальных, конечно, но и на них поиграть мы сможем. А вообще перед нами новое непаханое поле, которое мы только увидели. В голографическом мире мы можем придумать много нового, что-то даже открыть — и не только физическое, но и принадлежащее миру математики или химии. Я думаю, свой вывод каждый сформулировал для себя сам. Для интересующихся я оставляю библиографический список с источниками и с интересными материалами по этой теме:
Самодостаточная для популярного понимания энтропийной гравитации статья на Википедии (ссылка);
Статья «Информация в голографической Вселенной» на Modern Cosmology (ссылка);
Оригинальная статья Эрика Верлинде (ссылка), а также перевод этой статьи Михаилом Ханановичем Шульманом (ссылка);
Статья «Entropic Acceletating Universe» на arXiv.org (Easson et al., ссылка);
Статья «Голографический принцип — первая встреча» на Modern Cosmology (ссылка);
Моя статья об энтропии «Просто об энтропии: без формул и с бытовыми примерами» (ссылка);
Статья «Черные дыры и голограммы» на Хабре (ссылка);
Супер-пупер статья о голографическом принципе на английском (ссылка).
Ну и напоминаю, о том, чтобы читатель не стеснялся задать вопрос или поправить меня в комментариях. Также у меня есть телеграм-канал, где я рассказываю о последних новостях космологии и астрофизики, а также пишу об астрофотографии. Пишите мне в личку или наш чат. Всем добра!