Зачем (затем, что нужно кормить баллистическую модель)
Для построения траекторий КА и их носителей нужны данные. В первую очередь - аэродинамические. Они нужны при определении сил и моментов, действующих на космический аппарат (или его ступень), а также для оценки теплового состояния конструкции. Характеристики зависят от внешнего вида КА и параметров полета и обычно выглядят как обширные простыни с зависимостями соответствующих коэффициентов от углов атаки, чисел Маха, высот и много еще чего.
Есть несколько способов получить эти цифры:
CFD. Всякие ANSYS, floEFD, solidWorks flow simulation и так далее. Большие и серьезные программные пакеты с серьезным ценником. И для стартапа, пилящего свой шаттл в гараже, такой софт обойдется приблизительно во столько же, во сколько и сам гараж.
Приближенные графоаналитические методы. Потому что люди уже давно запускают в воздух и вакуум самые разные девайсы. Данные по их обтеканию в трубах и свободном потоке занесены в справочники, табулированы и параметризованы по удлинениям, углам стреловидности, толщинам профилей и так далее и тому подобное. Проблема таких подходов - в необходимости "на глаз" работать с различными книгами и атласами характеристик, переносить цифры с бумаги в электронный вид и страдать, страдать, страдать, когда геометрия приобретает формы, отличные от "цилиндроконический корпус с тонким крылом"
Приближенные методы на базе локальных параметров обтекания. Занимают промежуточное положение между первыми двумя и основаны на разбиении геометрии исследуемого ЛА на фрагменты, взаимодействием между которыми можно пренебречь. Поскольку возмущения в потоке не могут распространяться быстрее скорости звука и за пределы скачков уплотнения, то подобные методы лучше всего работают на больших скоростях (M ~ 8-10 и выше). Ими мы и займемся
Два основных метода - метод касательных клиньев и метод Ньютона. В каждом из методов поверхность ЛА дробится на элементарные площадки, затем определяется местный угол атаки (между плоскостью и набегающим потоком). В методе локальных скачков угол атаки сравнивается с максимальным допустимым (после него скачок отходит от поверхности), затем определяется степень повышения давления в потоке.

В методе Ньютона предполагается, что в избыточное давление превратится вся та часть удельного импульса потока, что шла по нормали к обтекаемой поверхности.

Если же угол - отрицательный, то поток испытывает разрежение, которое для малых углов хорошо аппроксимируется. Если угол превышен, то поток при обтекании тупого угла разрежается до вакуума (во всяком случае, давление на поверхности становится нулевым)
Зная габариты ЛА, можно определить его омываемую поверхность и характерный габарит. С этими цифрами на основе расчетно-экспериментальных данных можно вычислить коэффициент трения плоской пластины и дополнить им коэффициент сопротивления ЛА.

Отдельно выступает случай сильно разреженного газа (определяется числом Кнудсена, зависящим от скорости, плотности и габаритов ЛА). В этом случае метод Ньютона модифицируется с учетом произвольного движения молекул газа после столкновения с поверхностью
Все превратится в треугольники
Теперь нужно получить данные о геометрии ЛА. Есть множество форматов, но самым удобным кажется STL. Каждая запись исчерпывающе описывает элементарную площадку на поверхности тела через три точки, которые ее формируют, и ориентированный вектор нормали. А еще Blender, которым я достаточно сносно владею, умеет экспортировать в него модели. Однако есть нюанс - STL, создаваемый Blender-ом - это бинарный файл, чтение которого немного отличается от работы с привычными текстовыми файлами (csv, json и так далее). Но для таких оказий в NodeJS есть класс Buffer. А сам бинарный STL снабжен подробной документацией.
Для начала через поставляемый в fs метод open открываем на чтение бинарник, после чего из полученных сведений выбираем поле size и создаем нужный нам буфер для чтения данных.
Это код работы с STL

Дальнейшие действия определяются спецификацией бинарного STL. Первые 80 байтов - это заголовок со сведениями о программе, в которой был создан бинарник. Их можно пропустить. Следующие 4 байта критичны - это 32-разрядный Unsigned Int, хранящий количество треугольников в составе модели. Как только мы узнали количество треугольников - начнем их считывать.
Каждый треугольник состоит из идущий подряд 32-разрядных Float Little Endian. Первые три числа - приведенная к единичному вектору нормаль. Затем тройки точек (X, Y, Z), задающих плоскость. После 48 значащих байтов идет еще 2 байта с 16-разрядным Unsigned Int, который некоторые редакторы используют для сохранения цвета поверхности. Но для расчета обтекания цвет нам явно не потребуется.
Тест 1. Притупленное тело
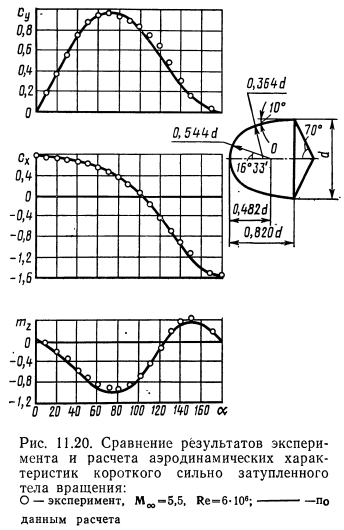
Для первого расчета выберем скругленный конус с тупоугольной кормой. Во-первых, на такой геометрии можно отловить все возможные случаи от торможения потока на скругленном носке до обтекания кормового среза с разрежением до вакуума. А во-вторых, по этой геометрии есть данные аналитического расчета и результаты аэродинамической продувки, которые послужат эталоном (К сожалению, модель отрисована в размере, не дающем совпадения по Рейнольдсу)
Это модель

На качественном уровне поведение коэффициентов нормальной и продольной силы совпадает с теоретическим расчетом. На количественном уровне есть расхождение в 5-10% относительно теории:
Теория и модель

Тест 2. Аполлон
Следующий шаг - "Аполлон". Сравним аэродинамическое качество из статьи DSMC Simulations of Apollo Capsule Aerodynamics... (которой я пользовался в посте про капсульные корабли) с модельным.
Аэродинамика "Аполлона"


График качества с высоты 85 км (где в полной мере применимы методы сплошной среды) с модельным расчетом. Как и в предыдущем случае, видна уверенная сходимость со средней погрешностью в ~5%. Кстати, обратим внимание на красный и синий графики качества из статьи AIAA - аэродинамическое качество для разреженных потоков быстро уменьшается.
Тест 3. Крыло с тонким профилем
Главное ограничение метода - малые скорости, для которых уже нельзя пренебрегать взаимодействиями между разными участками обтекаемого тела. Особенно это заметно при решении задачи обтекания конуса при малых (M ~2 - 3) скоростях. Здесь метод будет давать завышенные коэффициенты ( особенно сопротивления).
Расчет в диапазоне скоростей M = 2 - 6 (коэффициент подъемной силы от угла атаки)

Первый график - Мах 2, второй - Мах 4, третий - Мах 6. Угол атаки - в градусах
По предварительным оценкам, полученная модель лучше всего подходит для определения характеристик КА при скоростях M > 3,5 - 4 и для высот до ~ 90 км. Однако расчет показывает хорошую сходимость начиная с M=4, а полученные цифры аэродинамического качества хорошо коррелируют с "барьером Кюхемана" .

А теперь - немного хулиганства (и спойлер к циклу следующих статей). Кажется, я начинаю понимать, как нам одолеть Илона Маска. И это - нулевой шаг к захвату мира.

А пока у меня появился инструмент, позволяющий оценивать характеристики самых разных пепелацев, причем в наиболее интересном с точки зрения атмосферного полета космических аппаратов коридоре высот и скоростей - с достаточно хорошей (~5%) точностью.
Если кому-нибудь интересно, то код живет здесь. Вдруг Вас настигнет творческий порыв, и Вы поможете мне одолеть дозвук, трансзвук и малый сверхзвук.