Привет, Хабр! При решении задачи о максимальном потоке я столкнулся с тем, что во всех мне известных источниках было дано формальное описание самих алгоритмов, что очень сильно затрудняло понимание изложенного материала. И в этой статье я попробую на базовом уровне разобрать Алгоритм Форда-Фалкерсона на конкретном примере, чтобы после прочтения данной статьи, вы хотя бы понимали основную суть самого алгоритма.
Постановка задачи
Имеется следующий ориентированный граф, в котором вес ребра обозначает пропускную способность между вершинами. Нужно найти максимальный поток, который можно пропустить из истокав сток
.
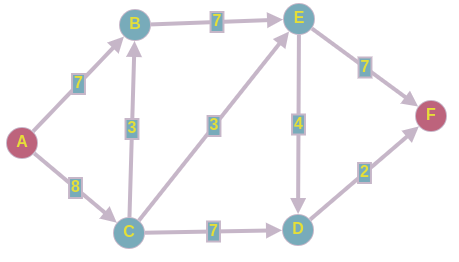
Как работает сам алгоритм?
Следует понимать остаточную сеть как тот же граф, который имеется на входе, но в этом случае мы будем производить над ним некоторые операции:
Отправлять определенное количество потока из текущей вершины в соседние.
Возвращать определенное количество потока из соседних вершин в текущую.
В начальный момент времени поток, который мы хотим провести через нашу сеть, должен быть равен нулю. Остаточная сеть совпадает с исходной сетью.
Находим любой путь из истока в сток в остаточной сети. Если путь не находим, утверждается, что поток является максимальным.
Пускаем через найденный путь поток равный минимальному весу ребра, которое входит в множество рёбер найденного пути.
Из веса рёбер на этом пути вычитываем размер потока, который мы пустили.
А к весу обратных рёбер (будем считать, что они существуют в остаточной сети и равны 0) прибавляем размер потока. Другими словами, на предыдущем шаге мы отправили некоторое количество потока из текущей вершины в следующую, а теперь при желании можем вернуть это же количество потока обратно в текущую.
Возвращаемся обратно к нахождению пути в остаточной сети после модификации.
Разбор конкретного примера
Разобьем одну итерацию проведения потока по выбранному пути на маленькие шаи, чтобы визуально стало понятно, как меняется остаточная сеть после проталкивания очередного потока.
Допустим наш алгоритм нашел следующий путь из вершины
в
нашей остаточной сети, которая на момент начала, совпадает с исходным графом.
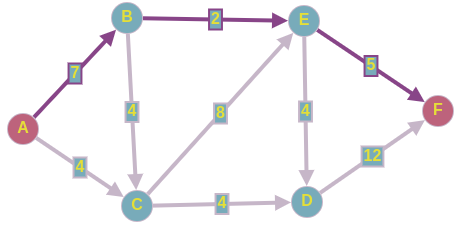
Сколько потока можем провести по этому пути???
- Больше2 ед.мы никак не сможем пустить, пропускаем наш поток по этим рёбрам из истока в сток.
Получаем следующее:
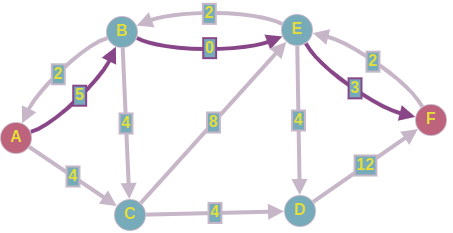
Рёбра с нулевым весом можно удалять. Таким образом, на первой итерации мы смогли увеличить максимальный поток на 2 ед.
Теперь дело за малым, остается всего лишь итерироваться до тех пор, пока существует путь из в
.
Допустим, на 2-ой итерации мы нашли такой путь в нашей остаточной сети:
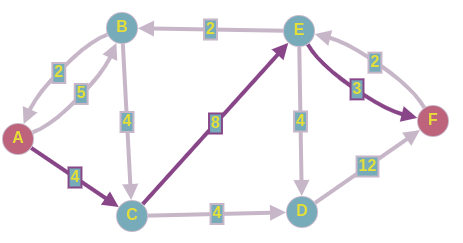
Пропускаем 3 ед. потока по этому пути, и перестраиваем остаточную сеть.
Получаем следующее:

На 3-ей итерации нашли такой путь в нашей модифицированной остаточной сети:

Пускаем 1 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:

На 4-ой итерации находим следующий путь в остаточной сети:
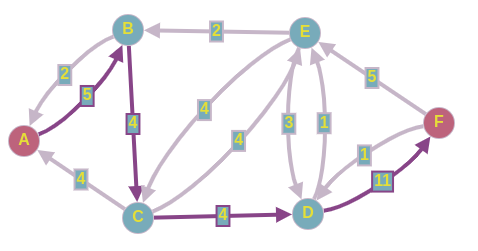
Пускаем 4 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:
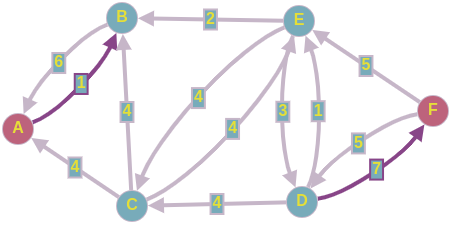
На этом этапе наш алгоритм прекратит выполнение из-за того, что пути из истока в сток не существует. И ответом к поставленной задаче будет служить сумма потоков всех найденных увеличивающихся путей.
Ответ: 10 ед.
Спасибо большое за внимание, надеюсь, был полезен!
Буду рад любым отзывам или поправкам для повышения доступности изложения материала!
Источники
Паша и Алгосы
Инструмент для работы с графами





