Ambrosia – Open Source-библиотека для работы с A/B-тестами

Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!

Всем привет! На связи Аслан Байрамкулов и Артем Хакимов из Big Data МТС. Мы вывели в Open Source первую версию библиотеки под названием Ambrosia. Ее назначение – работа с A/B тестами и экспериментами. В этой статье мы расскажем о функционале библиотеки и напомним о ключевых этапах А/Б-тестирования. Подробно про методологию проведения А/Б- тестов и различные тонкости и сценарии расскажем дополнительно в отдельных статьях.

В Open Source нам не удалось найти полноценного инструмента, который покрывал бы все этапы жизненного цикла A/B-тестирования, поэтому мы решили создать такой комплексный инструмент самостоятельно. Он пригодится всем, кто сталкивается в работе с A/B-тестами, в первую очередь аналитикам и data scientist.

Почему же Ambrosia? В мифологии Древней Греции амброзия – эликсир богов, дающий молодость и бессмертие. Аналогично наш инструмент нацелен на оживление культуры работы с экспериментами в компаниях.

Сейчас наш инструмент поддерживает:

теоретический и эмпирический дизайн экспериментов;
деление на группы (в том числе на множество групп, со стратификацией и так далее);
расчет эффекта с построением, как точечной, так и интервальной оценки;
использование нескольких подходов к увеличению чувствительности метрик: CUPED, MULTI_CUPED, MLVarianceReducer и другие;
возможность использование Spark API для дизайна и сплита.

Подробно ознакомиться с функционалом можно в туториалах (examples) и в документации.

Будем благодарны за ваш фидбэк, пожелания, замечания. Можно добавлять issues в github или писать в личку в Telegram @aslanbm. Также приветствуется участие в Open Source.

Рассмотрим основные этапы процесса А/Б-тестирования

Можно выделить три основных этапа, с которыми сталкивается исследователь при проведении А/Б-теста:

Дизайн эксперимента
Деление объектов по группам
Оценка результатов эксперимента после его завершения

А еще во многих задачах существует необходимость в определенной предобработке, трансформации и агрегации исходных данных, а также в организации дополнительных процессов.

Дизайн эксперимента

Перейдем к первому из этапов – дизайну будущего эксперимента. Предположим, что мы уже определились с гипотезой, которую хотим проверить, и с целевой метрикой, на основе которой будем делать выводы.

Теперь перед нами встает вопрос – какое количество объектов исследования необходимо включить в экспериментальные группы или какая должна быть длительность теста, чтобы мы смогли задетектировать эффект выбранного размера на уровне зафиксированных ошибок I и II рода. Может стоять и обратная задача: какой минимальный эффект на метрике мы сможем обнаружить с заданными ошибками I и II рода, если размер наших групп был зафиксирован.

Польза от дизайна А/Б-теста очевидна: мы достаточно точно моделируем параметры эксперимента и их значения и понимаем, насколько вообще эффективно и целесообразно проверять гипотезу. При большом количестве экспериментальных объектов мы будем эффективнее ими распоряжаться. В случае, если параметры эксперимента будут неподходящими, например, размер детектируемого эффекта окажется незначительным, мы откажемся от проведения напрасного эксперимента, сэкономив время и деньги.

Дизайн эксперимента довольно просто реализуется, если мы обладаем историческими данными о распределении метрики. Используя эту информацию, мы можем воспользоваться известной теоретической формулой оценки размера группы, либо начать семплировать группы различных размеров, и, моделируя ожидаемый эффект в тестовой группе, накапливать статистику по числу успешных срабатываний нашего критерия. В первом случае мы мгновенно получаем необходимое значение размера групп, основываясь на оценке среднего и дисперсии по имеющимся данным, а при эмпирическом подходе мы получаем искомый размер путем достижения необходимой нам мощности эксперимента.

Мы упомянули теоретическую формулу для расчета размера групп. Для того, чтобы освежить память, давайте остановимся на этой формуле.

Вывод теоретической формулы

Пусть у нас есть две выборки (X, Y), которые отвечают за наблюдения в каждой из групп (тестовая, контрольная). Тогда у нас есть нулевая гипотеза об идентичности групп против альтернативы о наличии эффекта.

$X = (X_1, ..., X_n)\\ Y=(Y_1, ..., Y_n)\\ H_0: \mu_y - \mu_x = 0 \\ H_1: \mu_x-\mu_x \ne 0 \\$

Тогда ошибки 1-го и 2-го рода могут быть записаны в следующем виде:

$P(|\overline{Y} - \overline{X}| \ge \varepsilon | \mu_y - \mu_x = 0) = \alpha \\ P(\overline{Y} - \overline{X} < \varepsilon | \mu_y = \mu_x (1+\delta)) = \beta \\$

Распишем левые части более подробно:

$P\Bigl(|\overline{Y} - \overline{X}| \ge \varepsilon | \mu_y - \mu_x = 0\Bigr) = 2P\Bigl(\overline{Y} - \overline{X} \ge \varepsilon|\mu_y-\mu_x=0\Bigr) = \\2P\Bigl(\sqrt{n}\frac{\overline{Y} - \overline{X} - (\mu_y - \mu_x)}{\sqrt{\sigma^2_x + \sigma^2_y}} \ge \sqrt{n}\frac{\varepsilon - (\mu_y - \mu_x)}{\sqrt{\sigma^2_x + \sigma^2_y}} | \mu_y - \mu_x = 0\Bigr) =\\ 2P\Bigl(\sqrt{n}\frac{\overline{Y} - \overline{X}}{\sqrt{\sigma^2_x + \sigma^2_y}} \ge \sqrt{n}\frac{\varepsilon }{\sqrt{\sigma^2_x + \sigma^2_y}}\Bigr) = \\2\Bigl(1 - P(\sqrt{n}\frac{\overline{Y} - \overline{X}}{\sqrt{\sigma^2_x + \sigma^2_y}} < \sqrt{n}\frac{\varepsilon}{\sqrt{\sigma^2_x + \sigma^2_y}})\Bigr) = \\2\Bigl(1-\Phi(\frac{\varepsilon\sqrt{n}}{\sqrt{\sigma^2_x + \sigma^2_y}})\Bigr) = \alpha\\$ $P\Bigl(\overline{Y} - \overline{X} < \varepsilon | \mu_y = \mu_x (1+\delta)\Bigr) = \\ P\Bigl(\sqrt{n}\frac{\overline{Y} - \overline{X} - (\mu_y - \mu_x)}{\sqrt{\sigma^2_x + \sigma^2_y}} < \sqrt{n}\frac{\varepsilon - (\mu_y - \mu_x)}{\sqrt{\sigma^2_x + \sigma^2_y}} | \mu_y = \mu_x (1+\delta)\Bigr) = \\ P\Bigl(\sqrt{n}\frac{\overline{Y} - \overline{X} - \mu_x\delta}{\sqrt{\sigma^2_x + \sigma^2_y}} < \sqrt{n}\frac{\varepsilon-\mu_x\delta }{\sqrt{\sigma^2_x + \sigma^2_y}}\Bigr) = \\ \Phi\Bigl(\sqrt{n}\frac{\varepsilon-\mu_x\delta }{\sqrt{\sigma^2_x + \sigma^2_y}}\Bigr) = \beta\\$

Получаем следующую систему из двух уравнений с функцией стандартного нормального распределения:

$\begin{equation} \begin{cases} \Phi(\frac{\varepsilon\sqrt{n}}{\sqrt{\sigma^2_x + \sigma^2_y}}) = 1-\frac{\alpha}{2} \\ \Phi(\sqrt{n}\frac{\varepsilon-\mu_x\delta }{\sqrt{\sigma^2_x + \sigma^2_y}}) = \beta \end{cases} \end{equation}\\$

Выразим эпсилон из каждого уравнения:

$\begin{equation} \begin{cases} \varepsilon = \Phi^{-1}(1-\frac{\alpha}{2})\sqrt{\frac{\sigma^2_x+\sigma^2_y}{n}} \\ \varepsilon = \Phi^{-1}(\beta)\sqrt{\frac{\sigma^2_x+\sigma^2_y}{n}}+ \mu_x\delta \end{cases} \end{equation}$

Откуда можем однозначно выразить минимальный размер выборки, необходимый для детектирования относительного эффекта:

$n = \frac{(\sigma^2_x+\sigma^2_y)(\Phi^{-1}(1-\frac{\alpha}{2}) - \Phi^{-1}(\beta))^2}{(\mu_x\delta)^2} = \frac{2\sigma^2(\Phi^{-1}(\frac{\alpha}{2}) + \Phi^{-1}(\beta))^2}{MDE_{absolute}^2}$

Из этой формулы можно вычленить MDE и рассчитать, какие эффекты можно фиксировать при различных размерах выборки.

Разобравшись с теоретическим подходом, реализуем дизайн эксперимента с помощью Ambrosia.

Представим, что перед нами стоит задача провести эксперимент по оценке улучшенной ML- системы рекомендаций услуг для клиентов МТС. Эта система была разработана нашими коллегами из команды RecTools. Она призвана заменить ручную работу персонала по определению оптимального набора услуг для продажи конкретному клиенту и повысить текущий объем продаж на имеющейся воронке.

При этом бизнес установил нам требование, что эффект, при котором они готовы перейти на новую ML-систему рекомендаций, в абсолютных числах составляет не менее 180 рублей в месяц на одну компанию. Срок эксперимента должен составить один бизнес-цикл, равный месяцу. Месячный срез данных – минимально возможный в рамках наших бизнес-процессов и, таким образом, в этом эксперименте мы будем наблюдать за начислениями клиентов в октябре.

Для того чтобы провести эксперимент и помочь коллегам подтвердить эффективность их разработки, нам необходимо:

определить оптимальный размер групп;
совершить разбиение выборки на контрольную и тестовую группы;
провести оценку результата по окончании эксперимента.

Выгрузим усредненные исторические значения метрики ежемесячных начислений клиентов, на основе которых будем проводить дизайн нашего эксперимента.

import pandas as pd

df = pd.read_csv('data/avg_historical_data.csv')

Импортируем из библиотеки класс Designer, предназначенный для дизайна экспериментов. Этот класс имеет единственный публичный метод run(), который на выходе возвращает dataframe с рассчитанным параметром эксперимента (это может быть любой параметр из тройки: мощность, минимальная величина эффекта и размер групп) для указанной нами метрики. В случае, если необходимо произвести дизайн для списка метрик - полученные dataframe упаковываются в словарь.

from ambrozia.designer import Designer

Теперь нам необходимо создать экземпляр класса-дизайнера. Передадим в конструктор класса dataframe с историческими данными о метрике, которую мы будем дизайнить, в нашем случае это помесячные начисления компаний.

На самом деле, мы можем передать этот dataframe позднее, уже в качестве аргумента метода run(). Точно также мы можем поступить и с большей частью параметров, относящихся непосредственно к эксперименту (ошибки, эффекты, и так далее), – либо передать их в конструктор при инициализации (и тогда они станут атрибутами созданного экземпляра), либо же передать их потом, во время исполнения метода run(). В случае неоднозначности выбора параметра, приоритет перед значением атрибута отдается аргументу в методе.

Похожим образом устроены и остальные core классы Ambrosia – в большинстве они имеют один основной публичный метод run() и позволяют подтягивать необходимые для работы метода переменные двумя способами: из имеющихся атрибутов экземпляра, либо из переданных в метод аргументов.

experiment_designer = Designer(dataframe=df)

Зададим сетку параметров, в которой мы зафиксируем интересующие значения для нашего эксперимента. Так как мы хотим дизайнить размер групп, нам необходимы ошибки I и II рода и ожидаемые размеры эффектов. Мы могли бы передать точечные значения параметров эксперимента, но сетка позволит нам провести анализ и быть более гибкими.

first_type_errors = [0.2, 0.1, 0.05, 0.01]
second_type_errors = [0.3, 0.2, 0.1]
effects = [1.03, 1.05, 1.07, 1.1, 1.15, 1.20]

Перед тем как запустить дизайн эксперимента, нам надо определиться с методом дизайна. В текущей реализации это может быть теоретическая формула, эмпирические методы на основе сэмплирования подгрупп из имеющейся истории для произвольного критерия или бутстрап. Каждый подход имеет свои плюсы и минусы, и в реальном эксперименте должен быть аккуратно исследован. Кстати говоря, для бинарных метрик реализованы различные интервальные критерии, о которых можно подробнее прочитать в документации.

Предположим, что наши данные прошли необходимые проверки, и мы можем воспользоваться теоретической формулой для расчета необходимых размеров групп. За выбор способа дизайна отвечает параметр method, передадим туда в качестве аргумента 'theory'.

experiment_designer.run(
    to_design='size',
    method='theory',
    effects=effects,
    first_type_errors=first_type_errors,
    second_type_errors=second_type_errors,
    metrics=['portfel_clc']
)

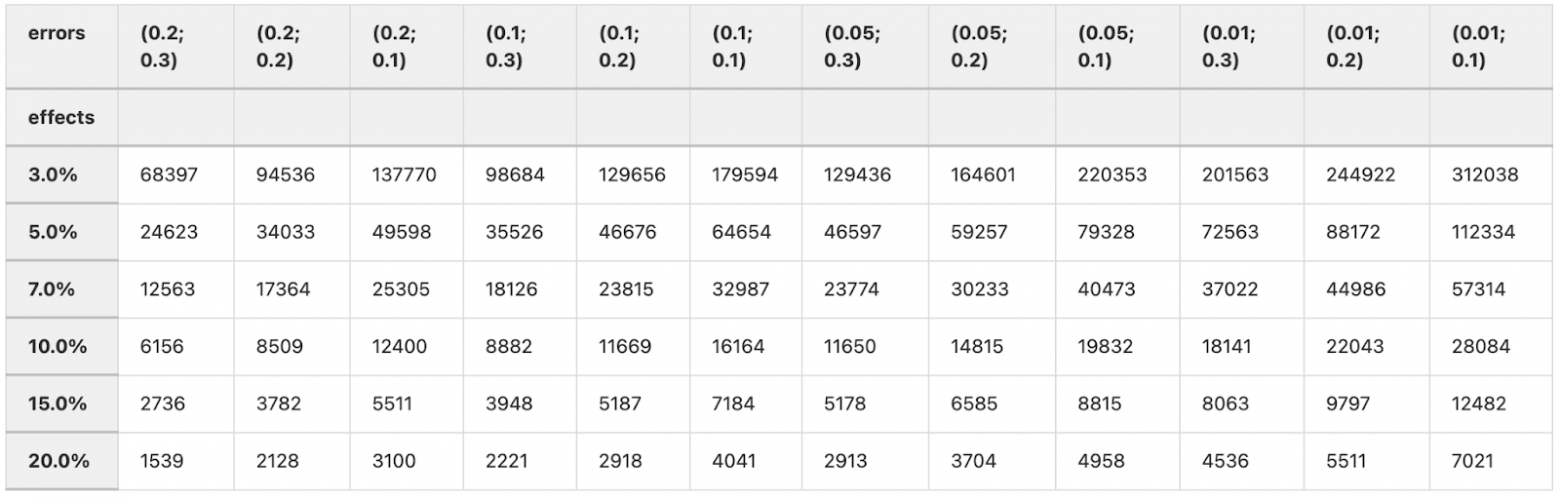
Итак, мы получили матрицу с расчетами требуемых размеров групп. Мы знаем, что для нашей бизнес конфигурации эксперимента подойдут значения до 15000 объектов в группе (максимальная пропускная способность наших каналов) и ошибки I рода = 0.05 и II рода = 0.2 (стандарт индустрии). Также помним о том, что для успешной интеграции модели нам необходимо в ходе эксперимента зафиксировать эффект не менее 180 рублей на одну компанию, что составляет ~15% в относительном выражении.

Анализируя таблицу, попробуем договориться с бизнесом о снижении порога принятия решения, чтобы при полном задействовании каналов повысить чувствительность нашего эксперимента с 15% до 10%. Бизнес соглашается с нашими доводами.

Класс Dеsigner обладает широким функционалом, который позволяет совершать дизайн экспериментов на основе исторических данных о распределении метрики, с помощью теоретических и эмпирических методов, на основе различных статистических критериев, таких как t-test, mannwhitney-test, bootstrap, и так далее. Для бинарных метрик можно пользоваться отдельной функцией design_binary, которая производит дизайн на основе исторического значения конверсии(удобно, в случае если вы точно знаете это число). Помимо этого, для ряда методов реализована поддержка PySpark DataFrame, что позволяет использовать spark таблицы аналогично версиям в pandas.

Сплит на группы

После того как параметры эксперимента определены и зафиксированы, следующий этап – создание экспериментальных групп необходимого размера. Существуют различные способы формирования групп (кстати, использование каждого подхода должно быть учтено соответствующим образом при дизайне эксперимента), часто применяются подходы с использованием хэширования – такой способ позволяют достичь детерминированности разбиения, и на основе набора методов сближения групп (самый простой способ – поиск в общем пуле для каждого объекта ближайшего к нему соседа по метрике). Помимо этого, можно отдельно выделить учет страт при разбиении, позволяющий уменьшить дисперсию групп, и получить оценку общей дисперсии генеральной совокупности точнее.

Вернемся, к нашему примеру с тестом новой системы ML-рекомендаций. Для нашего эксперимента необходимо сгенерировать две группы – контрольную и тестовую. В контрольной группе рекомендации будут строиться на основе экспертизы персонала, а в тестовой группе – в зависимости от предсказаний новой ML-системы.

За разбиение на группы в Ambrosia отвечает класс Splitter, импортируем его и выгрузим доступный пул id клиентов.

from ambrozia.splitter import Splitter

companies_pool = pd.read_csv('data/pool.csv')

Создадим экземпляр класса и передадим в конструктор dataframe с информацией о наших объектах, которые могут участвовать в эксперименте. Таблица должна содержать уникальные id объектов и опционально дополнительные признаки, которые мы можем использовать при стратификации и/или использовании метрического подбора.

experiment_splitter = Splitter(dataframe=companies_pool, id_column='id')

Зададим необходимый размер групп (параметр groups_size) и соль (параметр salt), так как мы хотим совершать разбиение с помощью хэширования id объектов. Такой подход при фиксации значения соли позволит сделать наше разбиение детерминированным и не хранить результирующую таблицу с группами где-то в базе.

groups_size = 15000
salt = 'ML_model_experiment322'

Совершим разбиение на контрольную и тестовую группы по хэшу, запустив метод run() с необходимыми параметрами. На выходе получаем новый dataframe необходимого размера с колонкой принадлежности к группе group.

experiment_splitter.run(
    method='hash',
    groups_size=groups_size,
    groups_number=2,
    salt=salt
)

В нашем примере мы собрали две группы с помощью разбиения по хэшу. Функционал Splitter не ограничен этим и позволяет совершать мультисплит на группы, учитывать при разбиении признаки для стратификации, и строить группы с подбором ближайшего соседа по метрике. Помимо этого есть удобная функция пост-генерации контрольной группы по уже существующей тестовой, которая получила воздействие в ходе эксперимента (~~или нет~~). Если дизайн и логика теста позволяют так поступить, то контрольная группа может быть сформирована на основе характеристик тестовых объектов из общей базы уже после после завершения эксперимента. Аналогично Designer в класс можно передавать PySpark DataFrame, что безусловно жизненно-необходимая функция для большинства подобных задач в Big Data.

Batch и real-time A/Б-тесты

Отметим, что предыдущий пример разбиения объектов на группы относится к случаю batch А/B-тестов. Это те эксперименты, которые производятся с использованием статических батчей данных, которые содержат необходимую информацию об объектах, их свойствах и метках принадлежности к группе.

К совсем другой категории относятся А/Б-тесты, в которых распределение трафика/объектов по группам происходит динамически в режиме онлайн. Примером эксперимента из такой категории может служить А/Б-тест по улучшению функционала корзины веб-сайта. В таком тесте объектами рандомизации могут выступать клиенты сервиса, а онлайн сплит-механизм будет предлагать им в зависимости от присвоенной метки старый или обновленный функционал корзины.

Нужно отметить, что, в отличии от batch А/Б-тестов, результат real-time тестов очень чувствителен к корректности настройки системы онлайн сплитования, что требует особой внимательности и осторожности, а желательно правильно настроенной платформы для проведения экспериментов.

Основной фокус актуального функционала библиотеки – на поддержке batch А/Б-тестов. Однако, это не означает, что при real-time сценарии эксперимента нельзя пользоваться методами дизайна или оценки эксперимента, – они все так же могут принести ощутимую пользу. В будущем в качестве одного из улучшений функционала Ambrosia мы предполагаем создание инструментов для онлайн сплита и необходимую адаптацию текущих методов под нужды real-time А/Б-тестов.

Оценка результата

Финальным логическим этапом в А/Б тестировании (помимо дальнейших выводов и решений) является статистическая оценка его результата. Обычно она состоит из точечного значения полученного эффекта, доверительного интервала и p-value полученного на основе выбранного статистического критерия. P-value/доверительный интервал – те величины, которые помогают нам в принятии решения о неслучайности полученного результата.

В случае нашего примера, из-за существующего бизнес цикла А/Б-тест закончился приблизительно через месяц, и мы можем произвести оценку получившегося результата на основе значений метрик в группах. Давайте посмотрим, как это можно сделать с помощью Ambrosia.

Для этого в Ambrosia реализован класс Tester.

Выгрузим значения метрик после эксперимента:

from ambrozia.tester import Tester

experiment_results = pd.read_csv('data/experiment_results.csv')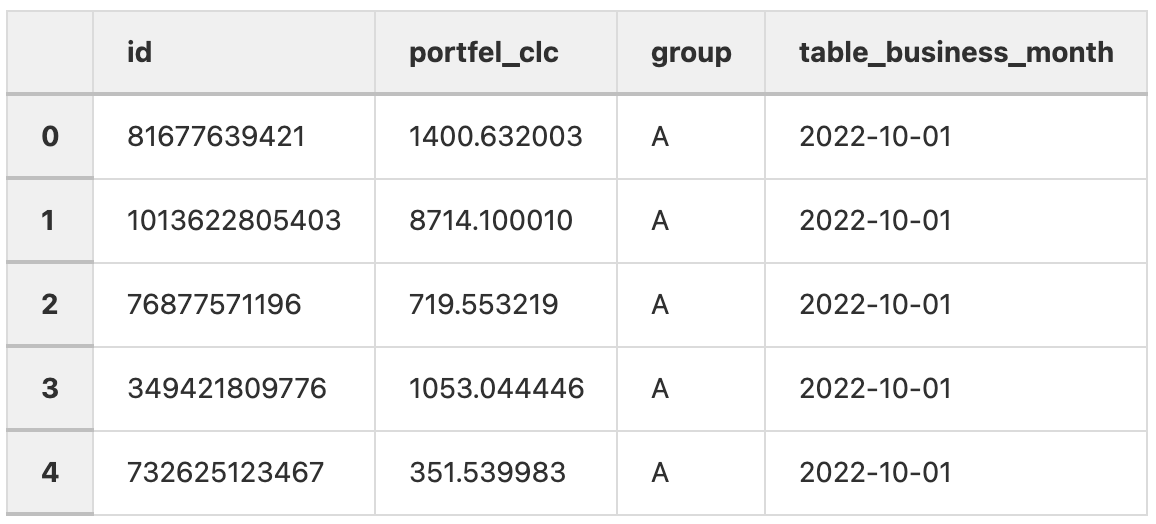

Метрики клиентов после окончания эксперимента

Передадим в конструктор класса dataframe с результатами и колонку, в которой указана метка принадлежности объекта к группе.

experiment_tester = Tester(
    dataframe=experiment_results,
    column_groups='group'
)

Подведем результаты прошедшего эксперимента на основе значений метрики начислений. Мы будет измерять относительный эффект (для этого в Ambrosia реализован дельта-метод) между группами и использовать t-test. Для этого передадим в параметр method значение 'theory' (классические статкритерии) и не забудем о зафиксированном нами на этапе дизайна значением ошибки I рода.

По умолчанию в качестве критерия в теоретическом методе оценки уже используется t-test, но мы могли бы передать в опциональный параметр criterion любой реализованный статистический критерий, например Mann-Whitney test. Запускаем метод run().

experiment_tester.run(
    effect_type='relative',
    method='theory',
    metrics='portfel_clc',
    first_errors=[0.05]
)

Итоговый вид оценки результата А/Б теста

На основании полученных результатов, эксперимент признан успешным: точечная оценка эффекта составила ~11% и является статистически значимой для зафиксированной нами ошибки I рода 0.05. Мы получили положительный результат и можем отправиться на встречу с бизнесом с хорошими новостями и грезить о выполненных годовых KPI.

Tester позволяет производить для экспериментов подобную оценку результатов на основе широкого ряда статистических критериев (парные, непараметрические критерии, бутстрап, бинарные критерии) и одновременно для нескольких групп с учетом коррекции МПГ(что полезно если вы, например, хотите протестировать за раз несколько вариантов ML-алгоритмов).

Методы ускорения экспериментов

В ряде сценариев А/Б-тестирования необходимый размер выборки/допустимая длительность эксперимента являются недостаточными для измерения эффектов интересующих масштабов, и возникает необходимость прибегать к различным методам повышения чувствительности экспериментов. Более того, ряд способов повышения чувствительности позволяет ценой небольших усилий начать быстро проводить большее число экспериментов и снизить стоимость их проведения, что несомненно является положительным фактором для компании, потому что позволяет за один и тот же промежуток времени протестировать больше гипотез и принять больше решений о внедрении изменений.

В Ambrosia мы в удобной форме реализовали несколько общеизвестных методов ускорения экспериментов – CUPED, MultiCUPED, а также метод сокращения дисперсии целевой переменной на основе предсказаний модели машинного обучения – MLVarianceReducer. Эти методы во многих случаях позволяют неплохо повысить чувствительность проводимых А/Б тестов и сохранить интерпретируемость метрик. В одной из наших следующих статей на основе конкретного эксперимента мы планируем продемонстрировать использование этих методов как части функционала Ambrosia и провести их сравнительную оценку по эффективности.

Планы и доработки

Несмотря на то, что библиотека уже сейчас имеет широкий функционал, позволяющий решать основные задачи А/Б-тестирования, мы планируем активно внедрять новые фичи и улучшать имеющиеся. На данный момент мы видим актуальные направления развития Ambrosia как:

Сбор фидбэка от сообщества, исправление найденных багов;
Внедрение PySpark в функционал Tester и в методы предобработки данных. Улучшение текущих методов для spark таблиц;
Реализация множества статистических методов на pyspark (~pyspark t-test, pyspark mw-test и так далее.);
Внедрение нового функционала: поддержка МПГ и групп разного размера в дизайне экспериментов, внедрение новых МПГ поправок при оценке результата А/Б теста и многое другое;
Создание класса для визуализации работы с A/Б тестами;
Создание класса для валидации корректности созданного А/Б пайплайна;
Дополнение примеров использования и туториалов.

Главным фокусом для нас сейчас является вывод библиотеки из первой версии в более устойчивое и надежное состояние на основе собранной обратной связи. В своей текущей архитектуре Ambrosia позволяет в несколько строк проводить основные этапы А/Б тестирования, и является легким, интуитивно понятным и не требующим глубокого погружения инструментом. Установление связи с целевой аудиторией позволит быстро совершать итерации по устранению багов и добавлению необходимого функционала.

Мы планируем развивать и улучшать Ambrosia, чтобы сделать этот инструмент еще более надежным и универсальным. Предлагаем всем заинтересованным и практикующим А/Б-тесты исследовать функционал библиотеки на своих задачах, и ждем обратной связи, issues на github и любого другого вклада в развитие открытого проекта Ambrosia.

Далее мы планируем продолжить выпуск статей, посвященных А/Б-тестированию, в которых будем освещать некоторые сценарии проведения экспериментов, а также наши исследования с использованием функционала Ambrosia.

Наши ссылки

ссылка на библиотеку;
чат для обсуждения библиотеки и A/Б-тестов;
авторы: Аслан Байрамкулов (tg: aslanbm), Артём Хакимов (tg: ad_hominem)

Источник: https://habr.com/ru/company/ru_mts/blog/700992/

Вернуться к списку

Интересные статьи

Что нужно знать перед началом работы с Ansible

Системы управления конфигурацией — незаменимые инструменты в арсенале разработчика и системного администратора. С их помощью можно автоматизировать рутинные операции по настройке окружения и деплоя, р...

Обход блокировки OpenVPN в Египте

Во время поездки в отпуск в Египет я приобрел сим карту местного оператора и решил посмотреть как быстро будет (по сравнению с традиционно медленным wifi отеля) работать интернет включая подключение к...

Бонус работы аналитиком данных: Как я нашел свой новый дом в Дублине

Наш сегодняшний перевод посвящен Data Science. Аналитик данных из Дублина рассказал, как искал себе жилье на рынке с высоким спросом и низким предложением. Я всегда завидовал тем про...

Как опыт работы инженером по сопровождению помог мне найти себя и выбрать профессию мечты

Привет, меня зовут Лиза. В этом посте я хочу рассказать о том, как в должности инженера по сопровождению попробовала себя в разных направлениях: поддержке, внедрении и анали...

Open RAN

Disclaimer: все написанное здесь — исключительно мое личное мнение, которое может не совпадать с мнением моего работодателя (Intel Corporation) и организации The 3rd Generation Partnershi...