Автоматическое создание траектории движения руки в анимации

Описание проблемы

Всем привет. В последнее время я занимаюсь созданием простых анимационных роликов. Недавно столкнулся со следующей проблемой -- мой персонаж должен коснуться звонка перед входом в квартиру пальцем руки. Скелет руки представлен на Fig.1. Это трехзвенный механизм, имеющий шарнирное закрепление в точке O. Требуется, манипулируя углами α,β,γ, перевести точку A₃ (эффектор) в точку E , если такое движение возможно. Данная задача имеет традиционное решение. Известны начальные значения углов. Решаем обратную задачу манипулятора, описанную в многочисленных статьях, и находим конечные значения углов α,β,γ. Каждый из интервалов между начальным и конечным значением угла разбивается на заданное число частей N . В результате получаем набор углов, с помощью которых получаем нужную траекторию движения руки. Поскольку для решения обратной задачи придётся решать нелинейные уравнения относительно углов, такой алгоритм не очень удобен. В книге Рик Парент "Компьютерная анимация" КУДИЦ-ОБРАЗ, М.:2004 предложено другое решение. К сожалению, изложение в упомянутой книге излишне абстрактно. В данной краткой статье представлена простая реализация алгоритма из этой книги. В конце статьи дана ссылка на ролик, в котором использован описанный метод.

Математическая модель и решение задачи

Ограничимся плоским случаем, хотя используемые уравнения легко адаптируются к трёхмерному случаю. Введём обозначения для длин костей

Все углы отсчитываются по часовой стрелке. В этих обозначениях координаты точки A₃ задаются уравнениями

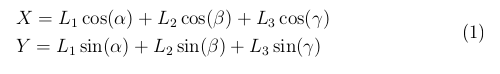
Fig.2 Кинематические уравнения скелета руки

Введём вектор Vec , соединяющий точки A₃ и E . Если мы правильно выбрали приращения углов dα,dβ,dγ, и точка A₃ приблизилась к E на величину dVec , то упомянутые приращения связаны уравнениями (2)

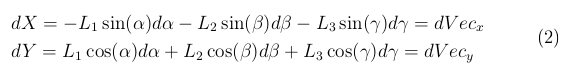
Имея два уравнения для трёх неизвестных приращений, мы не можем определить эти приращения однозначно. Выход заключается в использовании псевдообратной матрицы. В этом случае мы получаем одно из возможных решений системы (2). Это решение обладает свойством минимальности длины полученного вектора. Данное обстоятельство освобождает от опасности получить большое значение для какого-либо приращения. Теперь алгоритм построения траектории выглядит следующим образом.

• Устанавливаем начальные значения углов и коэффициент Coe<1

• В цикле

  • Находим положение эффектора

  • Находим вектор Vec из эффектора в точку E

  • Находим dVec= Coe*Vec и вычисляем приращения углов с помощью (2)

  • Находим новые углы и проверяем расстояние от эффектора до E

Ниже приведена реализация этого алгоритма с помощью библиотеки numpy.

import numpy as np
from numpy.linalg import pinv,norm

Angl = np.float_([1.2,.7,0]) #Alpha,Beta,Gamma
E = np.float_([30,-40]) # Point E
Bones = np.float_([50,45,3]) #L1,L2,L3
Coe = 0.1
Dist = 100
def oneStep(Angl):
    Cos = np.cos(Angl)
    Sin = np.sin(Angl)
    #Current coords eq (1)
    Matr = np.float_([Cos,Sin])
    Coords =  np.dot(Matr,Bones)
    Vec = E -Coords
    Dist = norm(Vec)
    #Calculate Delta eq(2)
    Matr = np.float_([-Sin*Bones,Cos*Bones])
    PInv = pinv(Matr) #pseudoinverse matrix
    dVec = Coe *Vec # dVec
    Delta = np.dot(PInv,dVec)
    return Angl+Delta,Dist

AllAngl = []
AllAngl.append(Angl)    
while Dist >2:
    Angl,Dist = oneStep(Angl)
    AllAngl.append(Angl)

Формально, требуется дополнительно следить за тем, чтобы рука в локтевом суставе не согнулась в обратную сторону. Поскольку это делается очевидным образом, проверка условия правильности сгиба не отражена в тексте программы.
Посмотреть на работу алгоритма можно здесь Пример анимации .