Вчера здесь вышла статья о быстром парсинге double, я зашёл во блог к её автору, и нашёл там ещё один интересный трюк. При сравнении чисел с плавающей точкой особое внимание приходится уделять NaN (восемь лет назад я писал про них подробнее); но если сравниваемые числа заведомо не NaN, то сравнить их можно быстрее, чем это делает процессор!
Положительные double сравнивать очень просто: нормализация гарантирует нам, что из чисел с разной экспонентой больше то, чья экспонента больше, а из чисел с равной экспонентой больше то, чья мантисса больше. Стандарт IEEE 754 заботливо поместил экспоненту в старшие биты, так что положительные double можно сравнивать просто как int64_t.
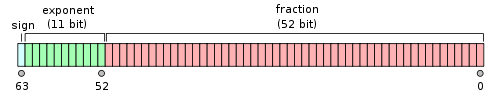
С отрицательными числами немного сложнее: они хранятся в прямом коде, тогда как int64_t — в дополнительном. Это значит, что для использования целочисленного сравнения младшие 63 бита double необходимо инвертировать (при этом получится -0. < +0., что не соответствует стандарту, но на практике не представляет проблемы). Явная проверка старшего бита и условный переход уничтожили бы всю выгоду от перехода к целочисленному сравнению; но есть способ проще!
Во блоге у Daniel Lemire несколько другой код (той же вычислительной сложности), но мой вариант сохраняет то полезное свойство, что
Положительные double сравнивать очень просто: нормализация гарантирует нам, что из чисел с разной экспонентой больше то, чья экспонента больше, а из чисел с равной экспонентой больше то, чья мантисса больше. Стандарт IEEE 754 заботливо поместил экспоненту в старшие биты, так что положительные double можно сравнивать просто как int64_t.

С отрицательными числами немного сложнее: они хранятся в прямом коде, тогда как int64_t — в дополнительном. Это значит, что для использования целочисленного сравнения младшие 63 бита double необходимо инвертировать (при этом получится -0. < +0., что не соответствует стандарту, но на практике не представляет проблемы). Явная проверка старшего бита и условный переход уничтожили бы всю выгоду от перехода к целочисленному сравнению; но есть способ проще!
inline int64_t to_int64(double x) {
int64_t a = *(int64_t*)&x;
uint64_t mask = (uint64_t)(a >> 63) >> 1;
return a ^ mask;
}
inline bool is_smaller(double x1, double x2) {
return to_int64(x1) < to_int64(x2);
}a>>63 заполняет все 64 бита копиями знакового бита, и затем >>1 обнуляет старший бит.Во блоге у Daniel Lemire несколько другой код (той же вычислительной сложности), но мой вариант сохраняет то полезное свойство, что
to_int64(0.) == 0