Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
В первой части части я перевел обученную модель полносвязной сети на базе Keras на работу с матричными вычислениями. Модель разработана для новостного агрегатора с целью фильтрации нежелательных новостей.
Но если посмотреть статью-руководство от tensorflow, можно увидеть, что одной из рекомендаций по классификации теста является использование сетей долгой краткосрочной памяти (LSTM).
Для моей задачи сеть прямого распространения обладает достаточным качеством, предсказуемостью и стабильностью результатов (объяснимое переобучение, влияние архитектуры сети на качество и т.д.). Ну и немаловажно - быстро обучается, в отличие от LSTM.
Но ради "академического" интереса обучим сеть c LSTM для бинароной классификации текста и переведем её также на работу только с матрицами и пакетом numpy. Это также наглядно покажет, как устроены ячейки LSTM.
Сеть LSTM
Итак, tensorflow рассматривает следующую архитектуру сети:
model = tf.keras.Sequential([
encoder,
tf.keras.layers.Embedding(
input_dim=len(encoder.get_vocabulary()),
output_dim=64,
# Use masking to handle the variable sequence lengths
mask_zero=True),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(64)),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(1)
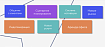
])Вот как она выглядит в графическом виде:

(https://www.tensorflow.org/text/tutorials/text_classification_rnn)
Модули TextVectorization и tf.keras.layers.Embeddingте же, что были в первой части моей работы. Вкратце напомню, что TextVectorization преобразует слова в уникальные числовые индексы, а Embedding затем преобразует их в плотные вектора.
Далее идет слой LSTM, который с помощью слоя tf.keras.layers.Bidirectional "проходится" по двум направлениям: от начала последовательности к концу и наоборот, а затем объединяет результаты. Но для начала надо смоделировать более простую архитектуру - без tf.keras.layers.Bidirectional, а зачем уже с ним.
Рассмотрим следующую модель:
model = tf.keras.Sequential([
tf.keras.layers.Embedding(
input_dim=len(encoder.get_vocabulary()),
output_dim=64,
mask_zero=True),
tf.keras.layers.LSTM(64),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])Для визуального понимания кода модели tf.keras.layers.LSTMрассмотрим типовую схему ячейки LSTM. На ней я подписал все функции, которые мы должны вычислить.

Получить веса обученной модели для этого слоя не так просто как для слоев Dense и Embedding - это делается следующим образом (вот тут про это хорошо написано):
# Количество ячеек памяти. Задается при объявлении слоя tf.keras.layers.LSTM(units)
units = int(int(model.layers[1].trainable_weights[0].shape[1])/4)
print("No units: ", units)
W = model.layers[1].get_weights()[0]
U = model.layers[1].get_weights()[1]
b = model.layers[1].get_weights()[2]
W_i = W[:, :units]
W_f = W[:, units: units * 2]
W_c = W[:, units * 2: units * 3]
W_o = W[:, units * 3:]
U_i = U[:, :units]
U_f = U[:, units: units * 2]
U_c = U[:, units * 2: units * 3]
U_o = U[:, units * 3:]
b_i = b[:units]
b_f = b[units: units * 2]
b_c = b[units * 2: units * 3]
b_o = b[units * 3:]Веса W используются при математических операциях с входной последовательностью x (т.е. выходом слоя Embedding). Веса U - для преобразования состояния h прошлой итерации. b - это смещение (bias).
Символ ![]() означает операцию
означает операцию np.multiply. Символ ![]() обычное поэлементное суммирование векторов.
обычное поэлементное суммирование векторов.
С учетом особенностей работы ячеек LSTM индексы с названиях коэффициентов обозначают "функциональное назначение" элементов:
Индекс "f" — функция забывания/forget gate. По сути, тут с помощью умножения на коэффициент от 0 до 1 управляется значением состояния Сt для удаления информации о прошлых шагах обработки. Код для вычисления:
# letter - это очередной символ из слоя Embedding
# h_st - выход предыдущей ячейки
self.f_t = self.sigmoid(np.dot(letter, self.W_f)
+ np.dot(self.h_st, self.U_f)
+ self.b_f)Индекс "i "— добавление информации к состояния, «входной вентиль». Здесь на основе выхода предыдущей ячейки ht-1 и ввода xt определяется, какие значения использовать из ввода (x) во внутреннем состоянии. Код:
# letter - это очередной символ из слоя Embedding
# h_st - выход предыдущей ячейки
self.i_t = self.sigmoid(np.dot(letter, self.W_i)
+ np.dot(self.h_st, self.U_i)
+ self.b_i)Индекс "с" — подготовка функции Ĉt
self.Ct_t = np.tanh(np.dot(letter, self.W_c)
+ np.dot(self.h_st, self.U_c)
+ self.b_c)Теперь все готово для расчета нового клеточного состояния Сt
self.state = np.multiply(self.f_t, self.state) + np.multiply(self.i_t, self.Ct_t)Индекс "о" - расчет выходного значения. Применяем гиперболический тангенс к текущему состоянию ячейки и умножаем на преобразованное значение текущего входного символа:
self.h_st = np.multiply(self.sigmoid(np.dot(letter, self.W_o)
+ np.dot(self.h_st, self.U_o)
+ self.b_o),
np.tanh(self.state))Полный код ячейки LSTM выглядит следующим образом.
def lstm(self, data):
# инициализация начального состояния ячейки и выходного состояния для работы на первой итерации
self.state=np.zeros(self.units)
self.h_st=np.zeros(self.units)
# проходим по символам в прямом направлении.
for letter in data:
self.f_t = self.sigmoid(np.dot(letter, self.W_f) + np.dot(self.h_st, self.U_f) + self.b_f)
self.i_t = self.sigmoid(np.dot(letter, self.W_i) + np.dot(self.h_st, self.U_i) + self.b_i)
self.Ct_t = np.tanh(np.dot(letter, self.W_c) + np.dot(self.h_st, self.U_c) + self.b_c)
self.state = np.multiply(self.f_t, self.state) + np.multiply(self.i_t, self.Ct_t)
self.h_st = np.multiply(self.sigmoid(np.dot(letter, self.W_o) + np.dot(self.h_st, self.U_o)+ self.b_o), np.tanh(self.state))
return np.array(self.h_st)Bidirectional LSTM
В случае использования tf.keras.layers.Bidirectional создается два слоя LSTM: один проходит цепочку слов в прямом направлении, второй - в обратном. Зачем результаты конкатенируются.
В результате обучения у нас получает две группы весов (для LSTM прямого и обратного направления соответственно) . Веса получают из обученной модели следующим образом:
self.vocal_dict = {vocal_dict[k]: k for k in range(len(vocal_dict))}
self.units = units
# слой прямого прохождения
self.W_farward = lstm_weights[0]
self.U_farward = lstm_weights[1]
self.b_farward = lstm_weights[2]
self.W_i_farward = self.W_farward[:, :self.units]
self.W_f_farward = self.W_farward[:, self.units: self.units * 2]
self.W_c_farward = self.W_farward[:, self.units * 2: self.units * 3]
self.W_o_farward = self.W_farward[:, self.units * 3:]
self.U_i_farward = self.U_farward[:, :self.units]
self.U_f_farward = self.U_farward[:, self.units: self.units * 2]
self.U_c_farward = self.U_farward[:, self.units * 2: self.units * 3]
self.U_o_farward = self.U_farward[:, self.units * 3:]
self.b_i_farward = self.b_farward[:self.units]
self.b_f_farward = self.b_farward[self.units: self.units * 2]
self.b_c_farward = self.b_farward[self.units * 2: self.units * 3]
self.b_o_farward = self.b_farward[self.units * 3:]
# слой обратного прохождения
self.W_backward = lstm_weights[3]
self.U_backward = lstm_weights[4]
self.b_backward = lstm_weights[5]
self.W_i_backward = self.W_backward[:, :self.units]
self.W_f_backward = self.W_backward[:, self.units: self.units * 2]
self.W_c_backward = self.W_backward[:, self.units * 2: self.units * 3]
self.W_o_backward = self.W_backward[:, self.units * 3:]
self.U_i_backward = self.U_backward[:, :self.units]
self.U_f_backward = self.U_backward[:, self.units: self.units * 2]
self.U_c_backward = self.U_backward[:, self.units * 2: self.units * 3]
self.U_o_backward = self.U_backward[:, self.units * 3:]
self.b_i_backward = self.b_backward[:self.units]
self.b_f_backward = self.b_backward[self.units: self.units * 2]
self.b_c_backward = self.b_backward[self.units * 2: self.units * 3]
self.b_o_backward = self.b_backward[self.units * 3:] Реализация tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(units)) таким образом, следующая:
def lstm_farward(self, data):
self.state=np.zeros(self.units)
self.h_st=np.zeros(self.units)
for letter in data:
self.f_t = self.sigmoid(np.dot(letter, self.W_f_farward) + np.dot(self.h_st, self.U_f_farward) + self.b_f_farward )
self.i_t = self.sigmoid(np.dot(letter, self.W_i_farward) + np.dot(self.h_st, self.U_i_farward) + self.b_i_farward )
self.Ct_t = np.tanh( np.dot(letter, self.W_c_farward) + np.dot(self.h_st, self.U_c_farward) + self.b_c_farward )
self.state = np.multiply(self.f_t, self.state) + np.multiply(self.i_t, self.Ct_t)
self.h_st = np.multiply(self.sigmoid(np.dot(letter, self.W_o_farward) + np.dot(self.h_st, self.U_o_farward)+ self.b_o_farward), np.tanh(self.state))
return np.array(self.h_st)
def lstm_backward(self, data):
self.state=np.zeros(self.units)
self.h_st=np.zeros(self.units)
for letter in data[::-1]:
self.f_t = self.sigmoid(np.dot(letter, self.W_f_backward) + np.dot(self.h_st, self.U_f_backward) + self.b_f_backward )
self.i_t = self.sigmoid(np.dot(letter, self.W_i_backward) + np.dot(self.h_st, self.U_i_backward) + self.b_i_backward )
self.Ct_t = np.tanh( np.dot(letter, self.W_c_backward) + np.dot(self.h_st, self.U_c_backward) + self.b_c_backward )
self.state = np.multiply(self.f_t, self.state) + np.multiply(self.i_t, self.Ct_t)
self.h_st = np.multiply(self.sigmoid(np.dot(letter, self.W_o_backward) + np.dot(self.h_st, self.U_o_backward)+ self.b_o_backward), np.tanh(self.state))
return np.array(self.h_st)
emb_out = self.embedding(sentanence)
lstm_out_farward = self.lstm_farward(emb_out)
lstm_out_backward = self.lstm_backward(emb_out)
lstm = np.concatenate((lstm_out_farward, lstm_out_backward))Заключение
В данной статье приведено моделирования слоев tf.keras.layers.Bidirectional и tf.keras.layers.LSTM. Полученные модели могут использоваться для развертывания обученной модели на системах без необходимости установки пакета tensorflow, а также для изучения работы LSTM в образовательных целях.