Что делает ChatGPT… и почему это работает?

Просто добавляйте по одному слову...

То, что ChatGPT может автоматически генерировать что‑то, что хотя бы на первый взгляд похоже на написанный человеком текст, удивительно и неожиданно. Но как он это делает? И почему это работает? Цель этой статьи — дать приблизительное описание того, что происходит внутри ChatGPT, а затем исследовать, почему он может так хорошо справляться с созданием более‑менее осмысленного текста. С самого начала я должен сказать, что собираюсь сосредоточиться на общей картине происходящего, и хотя я упомяну некоторые инженерные детали, но не буду глубоко в них вникать. (Примеры в статье применимы как к другим современным «большим языковым моделям» (LLM), так и к ChatGPT).

Первое, что нужно понять, это то, что ChatGPT всегда пытается сделать «разумное продолжение» любого текста, который он получил на данный момент, где под «разумным» мы подразумеваем «то, что можно ожидать от кого‑то, увидев, что люди написали на миллиардах веб‑страниц и т. д.».

Допустим, у нас есть текст «Лучшая вещь в искусственном интеллекте — это его способность...». Представьте, что вы сканируете миллиарды страниц написанного человеком текста (скажем, в Интернете или в оцифрованных книгах) и находите все случаи этого текста, а затем смотрите, какое слово встречается дальше в каком проценте случаев. ChatGPT эффективно делает нечто подобное, за исключением того, что (как я объясню) он не смотрит на буквальный текст; он ищет нечто, что «подходит по смыслу». И в итоге выдаёт ранжированный список слов, которые могут следовать далее, вместе с «вероятностями»:

И что примечательно, когда ChatGPT делает что‑то вроде написания текста, то, по сути, он просто спрашивает снова и снова: «Учитывая текст на данный момент, каким должно быть следующее слово?» — и каждый раз добавляет новое слово. (Точнее, он добавляет «маркер», который может быть просто частью слова — вот почему он иногда может «придумывать новые слова»).

Ладно, на каждом шаге он получает список слов с вероятностями. Но какое из них он должен выбрать, чтобы добавить к тексту, который сейчас пишет? Можно подумать, что это должно быть слово с «самым высоким рейтингом» (т. е. то, которому была присвоена самая высокая «вероятность»). Но здесь в дело вступает немного магии. Потому что по какой‑то причине — возможно, однажды мы получим научное понимание — если мы будем всегда выбирать слово с наивысшим рейтингом, то получим, как правило, очень сухой текст, в котором нет «души» (и даже иногда повторяет слово в слово уже какой‑либо существующий). Но если иногда мы случайно будем выбирать слова с более низким рейтингом, то получим «более живой» текст.

Из‑за этого элемента случайности мы скорее всего будем получать каждый раз чуть‑чуть разный результат даже для одних и тех же входных данных. И, в соответствии с этой магией, существует определенный так называемый параметр «температуры», который определяет, как часто будут использоваться слова с более низким рейтингом. Для генерации текстов, как оказалось, лучше всего подходит «температура» 0,8. (Стоит подчеркнуть, что здесь нет никакой «теории»; это просто оказалось работоспособным на практике. И, например, понятие «температура» существует потому, что используются экспоненциальные распределения, знакомые из статистической физики, но нет никакой «физической» связи — по крайней мере, насколько нам известно).

Прежде чем мы продолжим, должен сказать, что в целях демонстрации я буду говорить не о ChatGPT (которая довольно сложна), а о более простой системой GPT-2, которая достаточно мала и может быть запущена на рядовом компьютере. И поэтому практически для всего, что я показываю, я смогу включить явный код на Wolfram Language, который вы можете запустить на своем компьютере. (Wolfram‑Математики у меня нет, так что я не смог проверить. Код для генерации каждого изображения есть в оригинальной статье, если на него кликнуть).

Например, вот как получить таблицу вероятностей, приведённую выше. Во‑первых, мы должны получить нейронную сеть, лежащую в основе «языковой модели»:

Позже мы заглянем внутрь этой нейронной сети и поговорим о том, как она работает. Но пока мы можем просто применить эту «модель сети» как черный ящик к нашему тексту и попросить найти 5 лучших слов по вероятности, которые, по мнению модели, должны следовать за ним:

Это позволяет получить результат и превратить его в структурированный «набор данных»:

Вот что произойдёт, если многократно «применять модель» — на каждом шаге добавляя слово, которое имеет наибольшую вероятность (в этом коде оно указано как «решение» из модели):

А что будет дальше? В нашем случае «температура» скоро опустится до нуля, что приведёт к довольно запутанному и повторяющемуся тексту:

Но что если вместо того, чтобы всегда выбирать «оптимальное» слово, иногда случайным образом выбирать слова, которые подходят чуть хуже (со «случайностью», соответствующей «температуре» 0.8)? Мы получим примерно такой текст:

И с каждым новым запуском генерации текст будет чуть отличаться из‑за этого элемента случайности. Вот 5 примеров:

Стоит отметить, что даже на первом шаге существует множество возможных «следующих слов» на выбор (при температуре 0,8), хотя их вероятности довольно быстро уменьшаются (и да, прямая линия на этом логарифмическом графике соответствует затуханию по степенному закону n-1, что очень характерно для общей статистики языка):

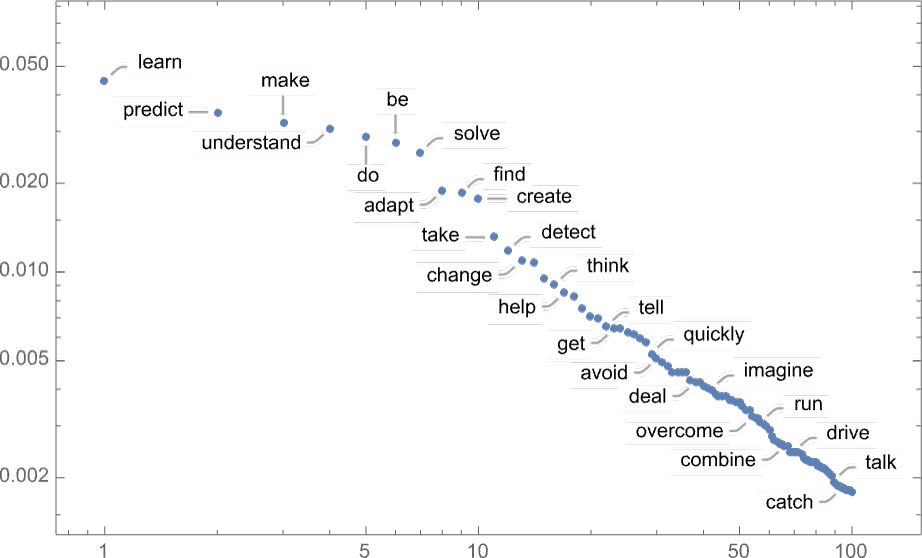
А что будет, если продолжить? Вот случайный пример. Это лучше, чем выбор всегда наиболее подходящего слова (нулевая температура), но все равно выглядит немного странно:

Это было сделано с помощью самой простой моделью GPT-2 (от 2019 года). С более новыми и большими моделями GPT-3 результаты лучше. Аналогичный пример для ChatGPT-3:

А вот случайный пример при «температуре 0,8»:

Откуда берутся вероятности?

Итак, ChatGPT всегда выбирает следующее слово на основе вероятностей. Но откуда берутся эти вероятности? Давайте начнем с более простой задачи — рассмотрим генерацию английского текста по одной букве (а не слову) за раз. Как мы можем определить, какова должна быть вероятность каждой буквы?

Самое простое — взять образец английского текста и подсчитать, как часто в нём встречаются различные буквы. Так, например, подсчитаем буквы в статье Википедии о «кошках»:

То же самое для «собак»:

Результаты похожи, но не одинаковы (логично, что буква «o» чаще встречается в статье о собаках, потому что она есть в самом слове «dog»). Тем не менее, если мы возьмем достаточно большую выборку английского текста, то результат будет более‑менее предсказуем:

Если просто сгенерируем последовательность букв с этими вероятностями, то получим:

Мы можем разбить это на «слова», добавляя пробелы, как если бы они тоже были буквами:

Результат станет чуть лучше, если мы учтём респределение «длин слов» для английского языка:

Мы до сих пор не получили ни одного «реального слова», но результаты выглядят чуть правдоподобнее. Однако, чтобы продвинуться дальше, нам нужно сделать нечто большее, чем просто выбирать каждую букву отдельно наугад. Например, мы знаем, что если у нас есть буква «q», то следующая буква чаще всего будет «u».

Вот график вероятностей для каждой из букв:

А вот график, показывающий вероятности пар букв («2-грамм») в типичном английском тексте. По горизонтали первая буква; по вертикали — последующая для неё:

И мы видим, что столбец «q» пуст (нулевая вероятность), за исключением строки «u». Хорошо, теперь вместо того, чтобы генерировать наши «слова» по одной букве за раз, давайте генерировать их, рассматривая по две буквы, используя эти «2-граммные» вероятности. Вот пример, который включает в себя уже несколько «реальных слов»:

Имея достаточно большой объём английского текста, мы можем получить довольно хорошие значения вероятностей не только отдельных букв или пар букв (2-грамм), но и для более длинных последовательностей. И если мы будем генерировать «случайные слова» с постепенно увеличивающимися последовательностями n‑грамм, то результат будет становиться всё более реалистичным:

Но давайте теперь предположим что мы имеем дело не с буквами, а со словами — примерно то, как это делает ChatGPT. В английском языке существует около 40 000 достаточно часто используемых слов. Проанализировав большой объём английских текстов (скажем, несколько миллионов книг, содержащих в общей сложности несколько сотен миллиардов слов), мы можем получить оценку частоты каждого слова. И используя это, мы можем начать генерировать «предложения», в которых каждое слово выбирается наугад с той же вероятностью, с которой оно встречается в тексте. Например:

Неудивительно, что это пока выглядит как бред. Как же мы можем улучшить результат? Как и в случае с буквами, мы можем начать учитывать не только вероятности для отдельных слов, но и вероятности для пар или более длинных последовательностей. Вот 5 примеров того, что мы можем получить для пар, во всех случаях начиная со слова «cat»:

Предложения становятся немного более осмысленными. И мы можем представить, что если бы мы могли использовать достаточно длинные n‑граммы, мы бы получили подобие ChatGPT — в том смысле, что оно генерировало бы последовательности слов длиной в небольшой текст с «правильными общими вероятностями». Но проблема в то, что нет даже близко достаточного количества когда‑либо написанных английских текстов, из которых можно было бы вывести эти вероятности.

В интернете может быть несколько сотен миллиардов слов; в книгах, которые были оцифрованы, может быть ещё сто миллиардов. Но даже при 40 000 регулярных слов число возможных 2-грамм составляет 1,6 миллиарда, а число возможных 3-грамм — 60 триллионов. Поэтому мы никак не можем оценить вероятности даже для всех этих слов из имеющегося текста. А когда мы доходим до «текстовых фрагментов» из 20 слов, количество возможных вариантов становится больше, чем количество частиц во Вселенной, так что в некотором смысле все они никогда не смогут быть записаны.

И что делать? Переходим на метауровень — давайте создадим модель, которая позволит нам оценить вероятность появления словосочетаний — даже если мы никогда не видели этих последовательностей слов в текстах, на которых обучались. И в основе ChatGPT лежит так называемая «большая языковая модель» (LLM), которая была построена для работы по оценке этих вероятностей.

Что такое модель?

Скажем, вы хотите узнать (как это сделал Галилей в конце 1500-х годов), сколько времени потребуется пушечному ядру, брошенному с разных этажей Пизанской башни, чтобы упасть на землю. Можно просто измерить это время в каждом случае и составить таблицу результатов. Или вы могли бы сделать то, что является сутью теоретической науки: описать модель системы, которая даёт некую формулу для вычисления ответа, чтобы не измерять и запоминать каждый случай отдельно.

Представим, что у нас есть (несколько идеализированные) данные о том, сколько времени занимает падение ядра с разных этажей:

Как выяснить сколько времени потребуется для падения с этажа, о котором у нас нет экспериментальных данных? Мы можем использовать известные законы физики, чтобы решить эту задачу. Но, допустим, у нас есть только данные, и мы не знаем, какие законы управляют ими. Тогда мы можем сделать математическое предположение, например, использовать в качестве модели прямую линию:

Мы можем выбрать разные по наклону прямые линии. Но именно эта в среднем ближе всего к нашим экспериментальным данным. И по этой прямой мы можем вычислить время падения с произвольного этажа.

Как мы догадались попробовать использовать здесь прямую линию? Вообще‑то, мы не знали. Просто это что‑то математически простое, а мы привыкли к тому, что многие данные, которые мы измеряем, хорошо ложатся на соответствующие математические примитивы. Мы могли бы попробовать что‑то математически более сложное — скажем, a + bx + cx^2 — и было бы лучше:

Однако, всё может пойти совсем не так. Например, вот лучшее, что может получиться с a + b/x + c*sin(x):

Стоит понимать, что никогда не существует «безмодельной модели». Любая модель, которую вы используете, имеет определённую базовую структуру и набор «ручек для настройки» (т. е. параметров, которые можно установить), чтобы соответствовать вашим данным. И в случае с ChatGPT используется множество таких «ручек» — фактически, 175 миллиардов.

Но удивительно то, что базовая структура ChatGPT с «всего лишь» таким количеством параметров — достаточна для создания модели, которая вычисляет вероятности следующего слова достаточно хорошо, чтобы дать нам разумные куски текста длиной в несколько абзацев.

Модели для задач человеков

Предыдущий пример включает в себя создание модели для числовых данных, которые получаются из простой физики, для которой применима «банальная математика». Но для ChatGPT мы должны сделать модель текста на человеческом языке, который будет парситься человеческим мозгом. А для чего‑то подобного у нас нет (по крайней мере, пока) ничего похожего на «простую математику». Так на что же может быть похожа такая модель?

Прежде чем говорить о языке, давайте поговорим о другой человекоподобной задаче: распознавании образов. В качестве простого примера рассмотрим изображения цифр (и да, это классический пример машинного обучения):

Для начала сделаем одну простую штуку — соберём кучу образцов изображений для каждой цифры:

Чтобы узнать, соответствует ли анализируемое изображение определённой цифре, мы могли бы просто провести явное попиксельное сравнение с имеющимися у нас образцами. Но мы, как люди, похоже, делаем нечто большее — потому что мы всё ещё можем распознавать цифры, даже если они написаны от руки и имеют всевозможные изменения и искажения:

Когда мы создавали модель для наших числовых данных выше, мы могли взять числовое значение x, которое нам было дано, и просто вычислить a + b*x для определенных a и b. Итак, если мы будем рассматривать значение уровня серого цвета каждого пикселя как некоторую переменную xi, существует ли функция от них, которая скажет какая цифра на картинке? Оказывается, такую функцию можно построить. Неудивительно, что она не особенно проста. Типичный пример может включать в себя около полумиллиона математических операций.

Но в итоге, если мы подадим в эту функцию набор значений пикселей для изображения, то получим достаточно точный ответ. Позже мы поговорим о том, как можно построить такую функцию, и об идее нейронных сетей. Но пока давайте рассматривать функцию как чёрный ящик, в который мы подаём изображения, скажем, рукописных цифр (в виде массивов значений пикселей) и получаем числа, которым они соответствуют:

А что если мы будем постепенно размывать цифру? Некоторое время наша функция всё ещё «распознаёт» её (здесь как «2»). Но вскоре она «теряется» и начинает выдавать «неправильный» результат:

Но почему мы говорим, что это «неправильный» результат? В данном случае мы знаем, что получили все изображения, размыв одну и ту же «2». Но если наша цель — смоделировать то, что что творится в голове у человека при распознавании изображений, то главный вопрос — как бы он ответил, получив одно из этих размытых изображений, не зная, откуда оно взялось.

Будем считать «хорошей моделю» ту, результаты которой как правило согласуются с теми, которые дал бы человек. И нетривиально, но факт — для задачи распознавания образов мы теперь знаем, как построить подобные функции.

Можем ли мы «математически доказать», что они работают? Ну, вообще‑то нет. Потому что для этого нам нужно иметь математическую теорию того, что мы, люди, делаем. Возьмём изображение «2» и изменим несколько пикселей. Если всего несколько пикселей «не на своем месте», то мы всё равно должны распознавать изображение как «2». Но как далеко это должно заходить? Это вопрос человеческого визуального восприятия. И да, ответ, несомненно, будет другим для пчёл или осьминогов — и потенциально совершенно другим для предполагаемых инопланетян.

Нейронные сети

Итак, как же на самом деле работают наши типичные модели для задач вида распознавания изображений? Наиболее популярный и успешный подход в настоящее время использует нейронные сети. Нейронные сети, изобретённые в форме, удивительно близкой к той, в которой они используются сегодня, в 1940-х годах, можно считать простой идеализацией того, как работает мозг.

В мозгу человека насчитывается около 100 миллиардов нейронов, каждый из которых способен производить электрический импульс до тысячи раз в секунду. Нейроны соединены в сложную сеть, причем каждый нейрон имеет древовидные ответвления, позволяющие ему передавать электрические сигналы тысячам других нейронов. И в грубом приближении, то, произведёт ли какой‑либо нейрон электрический импульс в данный момент, зависит от того, какие импульсы он получил от других нейронов, причём разные связи влияют на результат с разным «весом».

Когда мы «видим изображение», происходит следующее: фотоны света от изображения падают на клетки («фоторецепторы») в задней части наших глаз и генерируют электрические сигналы в нервных клетках. Эти нервные клетки передают сигнал другими нервными клетками, и в конечном итоге сигналы проходят через целую последовательность слоёв нейронов. Именно в этом процессе мы «распознаём» изображение, в конечном итоге «формируя мысль», что мы «видим 2» (и, возможно, произнесим слово «два» про себя).

Функция «чёрного ящика» из предыдущего раздела представляет собой «математическую» версию такой нейронной сети. Она имеет 11 слоёв (хотя «основных слоёв» только 4):

В этой нейронной сети нет глубокого «теоретического базиса»; это просто нечто, что ещё в 1998 году было создано как инженерное произведение и оказалось работоспособным. (Не сильно отличается от того, как был сформирован наш мозг в проецессе эволюции, не правда ли?).

Хорошо, но как такая нейронная сеть «распознаёт вещи»? Ключевым моментом является понятие аттракторов. Представьте, что у нас есть рукописные изображения 1 и 2:

Допустим, мы хотим, чтобы все «1» притягивались в одно место, а все «2» — в другое. Другими словами, если изображение каким‑то образом ближе к «1», чем к «2», оно должно оказаться ближе к 1 месту, и наоборот.

Небольшая аналогия: допустим, у нас есть определенные точки на плоскости, например, адреса кофеен. И мы хотим взять американо в ближайшей из них (т. е. всегда будем посещать одну ближайшую кофейню). Для этого разделим плоскость на области («бассейны аттракторов») с условными «водоразделами»:

Мы можем думать об этом как о реализации своего рода «задачи распознавания», в которой мы не определяем на какую цифру данное изображение «больше всего похоже» — скорее мы просто видим, к какому «бассейну» принадлежит данная точка. (Диаграмма Вороного, которую мы здесь показываем, разделяет точки в двумерном евклидовом пространстве; задачу распознавания цифр можно представить как нечто подобное, но в 784-мерном пространстве, сформированном из уровней серого всех пикселей каждого изображения).

Как же заставить нейронную сеть «выполнить задачу распознавания»? Давайте рассмотрим очень простой случай:

Наша цель — принять «входной сигнал», соответствующий позиции {x,y}, а затем «распознать» его как любую из трёх точек, к которой он ближе всего. Или, другими словами, мы хотим, чтобы нейронная сеть вычислила функцию от {x,y}, например:

Как же это сделать с помощью нейронной сети? В конечном счёте, она представляет собой связанную коллекцию идеализированных «нейронов», обычно расположенных в виде слоёв, простым примером которых является:

Каждый «нейрон» фактически настроен на оценку простой числовой функции. Чтобы «использовать» сеть, мы просто вводим числа (например, наши координаты x и y) сверху, затем нейроны на каждом слое «оценивают свои функции» и передают результаты дальше по сети — и конечный результат получается каким‑то таким:

В традиционной (биологической) схеме каждый нейрон имеет определённый набор «входящих связей» от нейронов предыдущего слоя, при этом каждой связи присваивается определённый «вес» (который может быть положительным или отрицательным числом). Значение данного нейрона определяется путём умножения значений «предыдущих нейронов» на их соответствующие веса, затем их суммирования и добавления константы, и, наконец, применения «пороговой» (или «активационной») функции. В математическом смысле, если нейрон имеет входы x = {x1, x2...}, то мы вычисляем f[w.x + b], где веса w и константа b обычно выбираются по‑разному для каждого нейрона в сети; функция f обычно одна и та же.

Вычисление w.x + b — это просто умножение и сложение матриц. «Функция активации» f вносит нелинейность (и в конечном итоге именно она приводит к нетривиальному поведению). Обычно используют различные функции активации; здесь мы остановимся только на Ramp (или ReLU):

Для каждой задачи нейронной сети (т. е. для каждой общей функции оценки), у нас будут разные варианты весов. (И — как мы обсудим позже — эти веса обычно определяются путём «обучения» нейронной сети с помощью машинного обучения на примерах нужных нам данных).

Каждая нейронная сеть просто соответствует некоторой общей математической функции — хотя она может быть и сложной для записи. Для приведённого выше примера это будет:

Нейронная сеть ChatGPT также представляет собой всего лишь математическую функцию, подобно этой, но оперирует миллиардами членов.

Но давайте вернёмся к отдельным нейронам. Вот несколько примеров функций, которые может вычислить нейрон с двумя входами (представляющими координаты x и y) при различных вариантах весов и констант (и Ramp в качестве функции активации):

Но как насчет более крупной сети сверху? Вот что она вычислит:

Это не совсем «правильно», но близко к функции «ближайшей точки», которую мы рассмотрели выше.

Давайте посмотрим, что происходит с некоторыми другими нейронными сетями. В каждом случае мы используем машинное обучение для поиска наилучшего набора весов. Затем мы показываем, что вычисляет нейронная сеть с этими весами:

Большие сети обычно лучше аппроксимируют функцию, к которой мы стремимся. И в «середине каждого бассейна аттрактора» мы обычно получаем именно тот ответ, который хотим. Но на границах — там, где нейронной сети «трудно принять решение» — всё может быть сложнее.

В этой простой математической задаче «распознавания» ясно, каков «правильный ответ». Но в задаче распознавания рукописных цифр всё не так однозначно. Что если кто‑то написал «2» так плохо, что она стала похожа на «7» и т. д.? Тем не менее, мы можем попросить её распознать следующие цифры, и вот что получится:

Можем ли мы сказать «математически», как сеть делает свои различия? Не совсем. Она просто «делает то, что делает нейронная сеть». Но оказывается, что обычно это довольно хорошо согласуется с различиями, которые делают кожаные.

Рассмотрим более сложный пример. Допустим, у нас есть изображения кошек и собак. И у нас есть нейронная сеть, которая была обучена различать их. Вот что она может сделать на некоторых примерах:

Теперь ещё сложнее понять, каков «правильный ответ». Как насчёт собаки, одетой в костюм кошки? Ну и так далее. Какой бы входной сигнал ни был получен, нейронная сеть генерирует ответ. И, как оказалось, делает это так, что это в достаточной степени соответствует ответу человека. Как я уже говорил выше, это не что‑то, что мы можем «вывести из первых принципов». Это просто то, что эмпирически было признано верным, по крайней мере, в определённых областях. Но это ключевая причина, по которой нейронные сети полезны: они каким‑то образом улавливают то, как эту задачу решает человек.

Посмотрите на фотографию кошки и спросите: «Почему это кошка?». Возможно, вы скажите: «Ну, я вижу её острые уши и т. д.». Но объяснить, как вы узнали в изображении кошку, не так‑то просто. Просто ваш мозг каким‑то образом догадался об этом. Но мы пока не знаем способа заглянуть внутрь мозга и посмотреть, как он это понял. А как насчёт (искусственной) нейронной сети? Ну, можно легко увидеть, что делает каждый «нейрон» при распознавании фотографии кошки. Но получить даже базовую визуализацию процесса обычно очень сложно.

В конечной сети, которую мы использовали для решения задачи «ближайшей точки», описанной выше, 17 нейронов. В сети для распознавания рукописных цифр их 2190. А в сети, которую мы используем для распознавания кошек и собак, 60 650 нейронов. Несколько проблематично визуализировать 60 650-мерное пространство, не так ли?. Но поскольку эта сеть настроена на работу с изображениями, многие слои нейронов в ней организованы в виде массивов, как массивы пикселей, на которые она смотрит.

И если мы возьмём типичное изображение кошки

то можем представить состояния нейронов первого слоя набором производных образов, многие из которых можем легко интерпретировать как «кошка без фона» или «контур кошки»:

К 10-му слою сделать это становится сложнее:

Но в целом можно сказать, что нейронная сеть «выбирает определённые признаки» (возможно, острые уши входят в их число) и использует их для определения того, что изображено на картинке. Но являются ли эти признаки теми, для которых у нас есть названия — например, «острые уши»? В основном нет.

Использует ли наш мозг схожие функции? Мы пока не знаем. Но примечательно, что первые несколько слоёв нейронной сети выбирают аспекты изображений (например, края объектов), которые похожи на те, что выбираются первым уровнем визуальной обработки в мозге.

Но допустим, мы хотим понять «теорию распознавания кошек» в нейронных сетях. Мы можем лишь заявить: «Смотрите, эта конкретная сеть решает эту задачу» — и сразу же понимаем насколько сложна проблема (и, например, сколько нейронов или слоёв может потребоваться). Но, по крайней мере, на данный момент у нас нет возможности «дать описательную часть» того, что делает сеть. Возможно, это потому, что она действительно несводима к вычислениям, и нет никакого общего способа узнать, что она делает, кроме явного отслеживания каждого шага. А может быть, дело в том, что мы ещё не «разобрались в науке» и не выявили «естественные законы», которые позволяют нам кратко описывать происходящее.

Мы столкнемся с теми же проблемами, когда будем говорить о генерации текстов с помощью ChatGPT. И снова неясно, есть ли способы «обобщить то, что он делает». Но богатство и детализация языка (и наш опыт работы с ним) могут позволить нам продвинуться дальше, чем с изображениями.

Машинное обучение и обучение нейронных сетей

До сих пор мы говорили о нейронных сетях, которые «уже знают», как выполнять определённые задачи. Но что делает нейронные сети такими полезными, так это то, что они не только могут в принципе выполнять все виды задач, но и постепенно «обучаются на примерах» для этого.

Когда мы создаём нейронную сеть для различия кошек и собак, нам не нужно писать программу, которая явно находит усы, например; вместо этого мы просто показываем множество примеров что такое кошка и что такое собака, а затем заставляем сеть «машинно учиться» различать на них.

Обученная сеть «обобщает» конкретные примеры, которые ей показывают. Как мы видели выше, дело не просто в том, что сеть распознаёт конкретный пиксельный рисунок изображения кошки, который ей показали; а скорее в том, что нейронная сеть каким‑то образом удаётся различать изображения на основе того, что мы считаем неким «общим свойством кошки».

Как же на самом деле происходит обучение нейронной сети? По сути, мы пытаемся найти такие веса, при которых нейронная сеть будет успешно отвечать на предоставленные нами примеры. А затем мы полагаемся на то, что нейронная сеть будет «интерполировать» (или «обобщать») их каким‑то «разумным» образом.

Рассмотрим ещё более простую задачу, чем задача о ближайшей точке. Попробуем просто заставить нейронную сеть выучить функцию:

Для этой задачи нам понадобится сеть, имеющая только один вход и один выход, например:

Но какие веса и т. д. мы должны использовать? При любом возможном наборе весов нейронная сеть будет вычислять некоторую функцию. Вот, например, как она работает с несколькими случайно выбранными наборами весов:

И да, мы видим, что ни в одном из этих случаев результат работы даже близко не воспроизводит нужную нам функцию. Так как же найти веса для этого?

Основная идея заключается в том, чтобы предоставить множество примеров «вход → выход» для «обучения на них», а затем попытаться найти веса, которые будут воспроизводить эти примеры. Вот результат выполнения этой задачи на всё большем количестве примеров:

На каждом этапе этого «обучения» веса в сети постепенно корректируются, и мы видим, что в конечном итоге мы получаем сеть, которая успешно воспроизводит нужную нам функцию. Как же мы регулируем веса? Основная идея заключается в том, чтобы на каждом этапе видеть, насколько мы далеки от получения нужной нам функции, а затем обновлять веса таким образом, чтобы приблизиться к ней.

Чтобы узнать, «как далеко мы находимся», мы вычисляем то, что обычно называется «функцией потерь» (или иногда «функцией затрат»). Здесь мы используем простую (L2) функцию потерь, которая представляет собой сумму квадратов разностей между полученными и истинными значениями. По мере обучения функция потерь постепенно уменьшается (следуя определённой «кривой обучения», которая отличается для разных задач), пока мы не достигнем точки, где сеть (по крайней мере, в хорошем приближении) успешно воспроизводит нужную нам функцию:

Итак, последний важный момент, который необходимо объяснить — это то, как корректируются веса для уменьшения функции потерь. Как мы уже говорили, функция потерь даёт нам «расстояние» между значениями, которые мы получили, и истинными значениями. Но «значения, которые мы получили», определяются на каждом этапе текущей версией нейронной сети — т. е. весами в ней. Но теперь представьте, что веса являются переменными — скажем, wi. Мы хотим выяснить, как настроить значения этих переменных, чтобы минимизировать потери, которые от них зависят.

Например, представьте (в невероятном упрощении типичных нейронных сетей, используемых на практике), что у нас есть только два веса w1 и w2. Тогда мы можем определить потерю как функцию от w1 и w2, которая выглядит следующим образом:

Численный анализ предоставляет множество методов для нахождения минимума в подобных случаях. Но типичный подход заключается в том, чтобы просто постепенно следовать по пути крутого спуска от любого предыдущего значения w1, w2, которое у нас было:

Это похоже на стекающую с горы реку. Всё, что мы можем утверждать — процедура закончится в каком‑то локальном минимуме поверхности («горное озеро»); она вполне может не достичь конечного глобального минимума.

Не очевидно, но найти самый крутой спуск на «весовом ландшафте» реально. На помощь приходит математика. Как мы уже говорили выше, нейронную сеть всегда можно представить как функцию, которая зависит от её входов и весов. Но теперь рассмотрим дифференцирование относительно этих весов. Оказывается, последовательное исчисление позволяет нам «распутать» операции, выполняемые каждым следующим слоем нейронной сети. В результате мы можем — по крайней мере, в некотором локальном приближении — «инвертировать» работу нейронной сети и постепенно находить веса, которые минимизируют потери, связанные с выходом.

На рисунке выше показана минимизация, которая может потребоваться в нереально простом случае, когда у нас всего 2 веса. Но оказывается, что даже при гораздо большем количестве весов (ChatGPT использует 175 миллиардов) минимизацию всё равно можно провести хотя бы с некоторым приближением. И фактически большой прорыв в «глубоком обучении», который произошёл примерно в 2011 году, был связан с открытием, что в некотором смысле может быть легче выполнить приблизительную минимизацию, когда задействовано много весов, чем когда их довольно мало.

Другими словами — несколько контринтуитивно — с помощью нейронных сетей может быть легче решать более сложные задачи, чем более простые. Вероятная причина этого, по‑видимому, заключается в том, что при большом количестве «весовых переменных» возникает высокоразмерное пространство с «множеством различных направлений», которые могут привести к минимуму, тогда как при меньшем количестве переменных легче застрять в локальном минимуме («горном озере»), из которого нет «направления, чтобы выбраться». Иными словами, чем больше путей, тем больше вероятность найти глобальный минимум.

Стоит отметить, что в типичных случаях существует множество различных наборов весов, которые дают нейронные сети с практически одинаковой производительностью. И обычно при практическом обучении делается много случайных выборов, которые приводят к «различным, но эквивалентным решениям», таким как эти:

Но каждое из таких решений будет иметь разное поведение. И если мы попросим, скажем, провести «экстраполяцию» за пределы области, в границах которой мы приводили учебные примеры, мы можем получить кардинально отличающиеся результаты:

Но какой из них «правильный»? На самом деле нет возможности сказать. Все они «согласуются с наблюдаемыми данными». Но все они соответствуют различным «врождённым» способам «думать» о том, что делать «за пределами коробки». И некоторые из них могут показаться нам, людям, «более разумными», чем другие.

Практика и теория обучения нейронной сети

За последние 10 лет мы серьёзно продвинулись в обучении нейронных сетей. Иногда — особенно в ретроспективе — можно увидеть некоторый момент «научного объяснения» того, как это работает. Но в основном всё было открыто методом проб и ошибок, путём реализации идей и хаков, которые постепенно сформировали значительный багаж знаний по работе с нейронными сетями.

Здесь есть несколько ключевых моментов. Во‑первых, это вопрос о том, какую архитектуру нейронной сети следует использовать для решения конкретной задачи. Затем возникает важный вопрос о том, как получить данные для обучения нейронной сети. И всё чаще речь не идёт об обучении сети с нуля: вместо этого новая сеть может либо непосредственно включать в себя другую, уже обученную, либо использовать её для генерации большего количества обучающих примеров для себя.

Можно было бы подумать, что для каждого конкретного вида задач нужна своя архитектура нейронной сети. Но было обнаружено, что одна и та же архитектура часто работает даже для, казалось бы, совершенно разных задач. На каком‑то уровне это напоминает идею универсального вычисления (и мой Принцип вычислительной эквивалентности), но я думаю, что это скорее отражение того факта, что задачи, которые мы обычно пытаемся заставить решать, являются «человекоподобными» — и нейронные сети могут улавливать довольно общие «человекоподобные процессы».

В ранние времена нейронных сетей существовала идея, что нужно «заставить нейронную сеть делать как можно меньше». Например, при преобразовании речи в текст считалось, что сначала нужно проанализировать звук речи, разбить его на фонемы и т. д. Но оказалось, что — по крайней мере, для «человекоподобных задач» — зачастую лучше просто попытаться обучить нейросеть «сквозной задаче», позволив ей самой «обнаружить» необходимые промежуточные характеристики, кодировки и т. д.

Существовала также идея о том, что в нейронную сеть следует вводить сложные отдельные компоненты, чтобы позволить ей «явно реализовать конкретные алгоритмические идеи». Но опять же, в основном это оказалось бессмысленным; вместо этого лучше просто иметь дело с очень простыми компонентами и позволить им «организовать себя» (хотя обычно непонятным для нас образом) для достижения (предположительно) эквивалента этих алгоритмических идей.

Это не значит, что не существует «структурирующих идей», которые были бы уместны для нейронных сетей. Так, например, наличие двумерных массивов нейронов с локальными связями оказывается очень полезным на ранних стадиях обработки изображений. А наличие моделей связности, которые концентрируются на «последовательном просмотре», оказывается полезным — как мы увидим позже — для работы с такими вещами, как человеческий язык, например, в ChatGPT.

Но важной особенностью нейронных сетей является то, что, как и компьютеры в целом, они в конечном итоге просто работают с данными. А современные нейронные сети — при существующих подходах к обучению — имеют дело именно с массивами чисел. Но в процессе обработки эти массивы могут быть полностью перестроены и изменены. В качестве примера, сеть, которую мы использовали для идентификации цифр выше, начинается с двумерного «похожего на изображение» массива, быстро «уплотняется» до многих каналов, но затем «сходится» в одномерный массив, который в конечном итоге будет содержать элементы, представляющие различные возможные выходные цифры:

Но как узнать насколько большая нейронная сеть нужна для решения определённой задачи? Это своего рода искусство. На каком‑то уровне главное знать «насколько сложна задача». Но для человекоподобных задач это обычно очень трудно оценить. Да, может существовать простой способ выполнить задачу в лоб с помощью компьютера. Но трудно сказать, есть ли то, что можно назвать хаками или короткими путями, которые позволяют выполнить задачу хотя бы на «человекоподобном уровне» гораздо легче. Для «механической» возможности играть в те же шахматы может потребоваться гигантское дерево состояний партии; но может существовать гораздо более простой («эвристический») способ достижения «человеческого уровня игры».

Когда имеешь дело с маленькими нейронными сетями и простыми задачами, иногда можно явно увидеть, что «отсюда туда не добраться». Например, вот лучшее, что можно сделать в задаче из предыдущего раздела с помощью нескольких маленьких нейросетей:

И что мы видим: если сеть слишком мала, она просто не может воспроизвести нужную нам функцию. Но выше определённого размера у неё нет проблем — по крайней мере, если обучать её достаточно долго и на достаточном количестве примеров. И, кстати, эти картинки иллюстрируют одну из легенд: часто можно обойтись меньшей сетью, если в середине есть «зажим», который заставляет всё проходить через меньшее промежуточное число нейронов. (Стоит также упомянуть, что сети без промежуточных слоев или так называемые «перцептроны» могут обучать только линейные функции, но как только появляется хотя бы один промежуточный слой, то становится возможным аппроксимировать любую функцию произвольно хорошо, по крайней мере, при наличии достаточного количества нейронов. Хотя для того, чтобы сделать её практически пригодной для обучения, обычно требуется некоторая регуляризация или нормализация).

Хорошо, предположим, что вы остановились на определённой архитектуре нейронной сети. Теперь встаёт вопрос о получении данных для обучения сети. Многие практические проблемы, связанные с нейронными сетями и машинным обучением в целом, сосредоточены на получении или подготовке необходимых обучающих данных. Во многих случаях («контролируемое обучение») необходимо получить явные примеры входных данных и ожидаемых от них результатов. Так, например, можно получить изображения, помеченные тем, что на них изображено, или каким‑либо другим атрибутом. И тут придётся их вручную размечать, что может быть сильно затратно. Но очень часто оказывается, что можно использовать то, что уже сделано, или использовать это как некий прокси. Так, например, можно использовать теги alt, которые были предусмотрены для изображений в Интернете. Или использовать закрытые субтитры, которые были созданы для видео. Или для обучения языковому переводу можно использовать параллельные версии веб‑страниц или других документов, существующих на разных языках.

Сколько данных нужно нейронной сети, чтобы натренировать её на выполнение определённой задачи? Это трудно оценить, исходя из первых принципов. Конечно, требования могут быть значительно снижены за счёт использования «трансферного обучения» для «передачи» таких вещей, как списки важных характеристик, которые уже были изучены другой сетью. Но в целом нейронные сети должны «видеть много примеров», чтобы хорошо обучаться. Для некоторых задач важной частью знаний о нейронных сетях является то, что примеры могут быть невероятно повторяющимися. И действительно, это стандартная стратегия — просто показывать нейросети все имеющиеся примеры снова и снова. В каждом из этих «раундов обучения» (или «эпох») нейросеть будет находиться в несколько ином состоянии, и каким‑то образом «напоминание» о конкретном примере полезно для того, чтобы заставить её «запомнить этот пример». (И да, возможно, это аналогично пользе повторения для запоминания людьми).

Но часто простого повторения одного и того же примера снова и снова недостаточно. Необходимо также показывать варианты в качестве примеров. И особенность нейросетей в том, что эти варианты «дополнения данных» не обязательно должны быть сложными, чтобы быть полезными. Просто слегка изменив изображения с помощью базовой обработки, можно сделать их по сути «новыми» для обучения нейронной сети. Аналогично, когда для обучения самоуправляемых автомобилей не хватает видео и т. д., можно перейти к получению данных из симуляций в модельной среде, похожей на видеоигру, без всех деталей реальных сцен.

Но вернёмся к ChatGPT. У него есть хорошая особенность — он может выполнять «обучение без контроля», что значительно упрощает получение примеров для обучения. Напомним, что основная задача ChatGPT — понять, как продолжить полученный текст. Поэтому для получения «обучающих примеров» достаточно получить фрагмент текста, замаскировать его конец, а затем использовать его в качестве «входа для обучения» — при этом «выходом» будет полный, незамаскированный фрагмент текста. Мы обсудим это подробнее позже, но суть в том, что, в отличие от обучения по изображениям, нет необходимости в явной разметке данных; ChatGPT может просто обучаться непосредственно на тех примерах текста, которые ему даны.

Хорошо, а как же сам процесс обучения нейронной сети? В конечном счёте, всё сводится к определению того, какие веса наилучшим образом отражают заданные обучающие примеры. И есть всевозможные подробные варианты и «настройки гиперпараметров» (так называемые, потому что веса можно рассматривать как «параметры»), которые можно использовать для настройки того, как это делается. Существуют различные варианты функции потерь (сумма квадратов, сумма абсолютных значений и т. д.). Существуют различные способы минимизации потерь (как далеко в пространстве весов перемещаться на каждом шаге и т. д.). И ещё есть вопросы, например, насколько много примеров нужно показать, чтобы получить каждую последующую оценку потерь, которые пытаются минимизировать. И да, можно применять машинное обучение для автоматизации машинного обучения и для автоматического задания таких вещей, как гиперпараметры.

В конечном итоге весь процесс обучения можно описать как постепенно уменьшающиеся потери (как в этом прогрессе Wolfram Language для небольшого обучения):

Обычно потери уменьшаются в течение некоторого времени, но в конце концов выравниваются до некоторого постоянного значения. Если это значение достаточно мало, то обучение можно считать успешным. В противном случае это признак того, что следует попробовать изменить архитектуру сети.

Можно ли определить, сколько времени должно пройти, чтобы «кривая обучения» выровнялась? Как и для многих других вещей, существует приблизительная зависимость масштабирования по степенному закону, которая зависит от размера нейронной сети и объёма используемых данных. Но общий вывод таков: обучить нейронную сеть сложно — и это требует больших вычислительных усилий. На практике подавляющее большинство этих усилий тратится на выполнение операций над массивами чисел, а именно в этом хороши графические процессоры, поэтому обучение нейронных сетей обычно ограничено доступностью графических процессоров.

Появятся ли в будущем принципиально лучшие способы обучения или механизмы работы нейронных сетей? Почти наверняка. Фундаментальная идея заключается в создании гибкой «вычислительной ткани» из большого числа простых (по сути, одинаковых) компонентов — и в том, чтобы эта «ткань» была такой, что её можно постепенно модифицировать для обучения на примерах. В современных нейронных сетях для такой постепенной модификации используются идеи исчисления — в применении к действительным числам. Но становится всё более очевидным, что высокая точность чисел не имеет значения; 8 бит или меньше может быть достаточно даже при использовании современных методов.

С вычислительными системами типа клеточных автоматов, которые в основном работают параллельно на многих отдельных битах, никогда не было ясно, как сделать её инкрементальную модификацию, но нет причин думать, что это невозможно. И на самом деле, как и в случае с «прорывом 2012 года в глубоком обучении», может оказаться, что такая постепенная модификация будет легче в более сложных случаях, чем в простых.

Нейронные сети — возможно, немного похожие на мозг — устроены таким образом, что имеют по сути фиксированную сеть нейронов, при этом изменяется сила связей («вес») между ними. (Возможно поэтому в молодом мозге также растёт большее количество совершенно новых связей). Но хотя это может быть удобной схемой для биологии, совершенно очевидно, что это даже близко не идеальный способ достижения нужной нам функциональности. И что‑то, что включает в себя эквивалент прогрессивного переписывания сети, в конечном итоге может оказаться лучше.

Но даже в рамках существующих нейронных сетей в настоящее время существует важное ограничение: обучение в том виде, в котором оно проводится сейчас, является принципиально последовательным, с эффектами каждой партии примеров, которые распространяются назад для обновления весов. И действительно, при современном компьютерном оборудовании — даже с учетом GPU — большая часть нейронной сети во время обучения значительную часть времени «простаивает», обновляется только одна часть за раз. В некотором смысле это происходит потому, что наши современные компьютеры имеют память, которая отделена от процессоров (или GPU). Но в мозге всё предположительно иначе: каждый «элемент памяти» (т. е. нейрон) также является потенциально активным вычислительным элементом. И если бы мы смогли настроить наше будущее компьютерное оборудование подобным образом, то скорее всего обучение стало бы гораздо более эффективным.

"Разумеется, достаточно большая сеть может сделать всё!"

Возможности чего‑то вроде ChatGPT кажутся настолько впечатляющими, что хочется думать, что если просто «продолжать» и тренировать всё большие и большие нейронные сети, то в конце концов они смогут «делать всё». И если речь идёт о вещах, которые легко доступны человеческому разуму, то вполне возможно, так оно и есть. Но за последние несколько сотен лет науки мы осознали, что есть вещи, которые могут быть описаны формальными процессами, но от этого они не становятся лёгкими для понимания.

Нетривиальная математика — один большой пример. В общем случае это всё равно вычисления, дальше речь идёт о феномене несводимости вычислений. Существуют некоторые вычисления, для выполнения которых потребуется много шагов, но которые на самом деле могут быть «сведены» к чему‑то довольно быстрому. Но открытие вычислительной несводимости подразумевает, что это не всегда работает. Вместо этого существуют алгоритмы, в которых для получения результата неизбежно требуется выполнить каждый шаг вычислений:

Наш мозг изначально спроектирован так, что ему трудно решать задачи, основанных на вычислительной несводимости. Чтобы заниматься математикой в уме, требуются особые усилия. И обычно на практике невозможно «продумать» шаги в работе любой нетривиальной программы не сбрасывая дамп на бумагу.

Но для этого у нас и есть компьютеры. С помощью них мы можем легко делать длинные, несводимые к вычислениям вещи. И ключевой момент в том, что в общем случае для них нет короткого пути.

Да, мы могли бы запомнить несколько конкретных примеров того, что происходит в какой‑то момент в конкретной вычислительной системе. И, возможно, мы даже сможем увидеть некоторые («вычислительно сводимые») закономерности, которые позволят нам сделать небольшое обобщение. Но вычислительная несводимость означает, что мы никогда не можем гарантировать, что не произойдёт непредвиденное, и только явно выполнив вычисления, можно быть уверенным в результате каждой итерации.

Существует фундаментальное противоречие между обучаемостью и вычислительной несводимостью. Обучение предполагает сжатие данных за счет использования закономерностей. Но вычислительная несводимость подразумевает ограниченное количество закономерностей.

С практической точки зрения можно представить себе встраивание небольших вычислительных моделей, таких как клеточные автоматы или машины Тьюринга, в обучаемые системы, такие как нейронные сети. И действительно, подобные плагины могут служить хорошим «инструментом» для нейронной сети, как Wolfram|Alpha может быть хорошим инструментом для ChatGPT. Но вычислительная несводимость подразумевает, что нельзя «проникнуть внутрь» этих устройств и заставить их обучаться.

Иными словами, существует конечный компромисс между возможностями и обучаемостью: чем больше вы хотите, чтобы система «действительно использовала» свои вычислительные возможности, тем больше она будет демонстрировать вычислительную несводимость, и тем меньше она будет обучаема. И чем больше она поддается обучению, тем меньше она будет способна выполнять сложные вычисления.

Для ChatGPT в его нынешнем виде ситуация на самом деле гораздо более экстремальная, потому что нейронная сеть, используемая для генерации каждого токена вывода, является чистой «feed‑forward» сетью (без циклов), и поэтому не имеет возможности выполнять какие‑либо вычисления с нетривиальным «потоком управления».

Конечно, можно задаться вопросом, действительно ли важно уметь выполнять несводимые вычисления. И действительно, на протяжении большей части человеческой истории это было не особенно важно. Но наш современный технологический мир построен на технике, которая использует как минимум математические вычисления, а всё чаще и более общие алгоритмы. И если мы посмотрим на мир природы, он полон несводимых вычислений, которые мы постепенно понимаем как имитировать и использовать в наших технологических целях.

Да, нейронная сеть, безусловно, может принять во внимание те или иные закономерности в естественном мире, которые мы замечаем с помощью «человеческого мышления без посторонней помощи». Но если мы хотим разобраться в математике или численных методах, нейросеть не сможет этого сделать — если только она не будет эффективно использовать «обычную» вычислительную систему.

Но во всём этом есть нечто потенциально непонятное. В прошлом существовало множество задач — в том числе написание текстов — которые, как мы полагали, были «принципиально слишком сложными» для компьютеров. А теперь, когда мы видим, как их выполняет ChatGPT, то склонны внезапно думать, что компьютеры должны стать намного мощнее — в частности, превзойти то, на что они уже были в принципе способны (например, итерировать циклы для вычислительных систем типа клеточных автоматов).

Но это не совсем правильный вывод. Вычислительно несводимые процессы всё ещё принципиально трудны для компьютеров — даже если компьютеры могут легко вычислять их отдельные этапы. Вместо этого мы должны сделать вывод, что задачи вроде написания текстов, которые мы, люди, могли бы выполнять, но не думали, что их могут выполнять компьютеры, на самом деле в некотором смысле вычислительно проще, чем мы думали.

Другими словами, причина, по которой нейронная сеть может быть успешной в этом, заключается в том, что подобная задача оказывается «вычислительно более мелкой» проблемой, чем мы думали. И в каком‑то смысле это приближает нас к «теории» того, как мы, люди, справляемся с подобными вещами и в частности с речью.

Если бы у вас была достаточно большая нейронная сеть, тогда да — вы могли бы делать всё то, что с легкостью может делать человек. Но вы не сможете сделать то, что может сделать мир природы в целом, или то, что могут сделать инструменты, которые мы создали на его основе. Именно использование этих инструментов — как практических, так и концептуальных — позволило нам в последние века выйти за пределы того, что доступно «чистому человеческому мышлению без посторонней помощи», и охватить для человеческих целей большее количество того, что есть в физической и вычислительной вселенной.

Концепция эмбеддингов

Нейронные сети — по крайней мере, в том виде, в котором они есть в настоящее время — основаны на числах. Поэтому, если мы хотим использовать их для работы с чем‑то вроде текста, нам понадобится способ представить наш текст числами. И мы могли бы начать с того, что просто присваивать номер каждому слову в словаре (по сути, как это делает ChatGPT). Но есть важный момент, который выходит за рамки этого. Это идея «эмбеддингов». Можно думать об эмбеддингах как о попытке представить «сущность» чего‑то массивом чисел — со свойством, что «подобные вещи» представлены близкими числами.

Так, например, мы можем думать об эмбеддингах слов как о расположении слов в своего рода «смысловом пространстве», в котором «близкие по смыслу» слова объединяются в скопления. Фактические эмбеддинги, которые используются, например, в ChatGPT, состоят из больших списков чисел. При проецировании их на плоскость получится что‑то типа такого:

И да, это удивительно хорошо передаёт типичные повседневные впечатления. Но как мы можем построить такие эмбеддинги? В общих чертах идея заключается в том, чтобы просмотреть большой объём текста (здесь 5 миллиардов слов из Интернета) и затем увидеть, «насколько похожи» фрагменты текстов, в которых появляются разные слова. Так, например, «аллигатор» и «крокодил» будут часто встречаться почти взаимозаменяемо в похожих предложениях, и это означает, что они будут располагаться рядом в эмбеддингах. Но «репа» (turnip) и «орел» (eagle), как правило, не встречаются в похожих предложениях, поэтому они будут располагаться далеко друг от друга.

Но как на самом деле реализовать нечто подобное с помощью нейронных сетей? Давайте начнём с построения эмбеддингов для изображений. Мы хотим найти способ охарактеризовать изображения списками чисел таким образом, чтобы «изображениям, которые мы считаем похожими», были присвоены похожие списки чисел.

Как определить «похожесть изображений»? Ну, если наши изображения представляют собой рукописные цифры, мы можем считать два изображения похожими, если они представляют собой одну и ту же цифру. Ранее мы обсуждали нейронную сеть, которая была обучена распознавать рукописные цифры. Мы можем считать, что она была настроена таким образом, что на выходе помещает изображения в 10 различных групп, по одному на каждую цифру.

Но что если «перехватить» то, что происходит внутри нейронной сети до принятия окончательного решения, что «это „4“? Можно ожидать, что там есть числа, которые характеризуют изображения как „в основном 4-подобные, но немного 2-подобных“ или что‑то в этом роде. И идея состоит в том, чтобы отобрать такие числа для использования в качестве элементов эмбеддинга.

Итак, концепция. Вместо того, чтобы напрямую пытаться определить «какое изображение находится рядом с каким другим изображением», мы рассматриваем чётко определенную задачу (в данном случае распознавание цифр). Тогда мы можем получить явные данные для обучения, а затем используем тот факт, что при выполнении этой задачи нейронная сеть неявно должна принимать «решения о близости». Таким образом, вместо того, чтобы явно отвечать о «близости изображений», мы просто смотрим ответ для конкретной задачи — какую цифру представляет изображение, а затем оставляем на усмотрение нейронной сети неявное определение того, что это подразумевает «близость изображений».

Как это работает для сети распознавания цифр? Мы можем представить её как состоящую из 11 последовательных слоёв (функции активации показаны как отдельные слои):

В начале мы подаём на первый слой реальные изображения, представленные двумерными массивами значений пикселей. А в конце — из последнего слоя — мы получаем массив из 10 значений, определяющих насколько сеть уверена, что изображение соответствует каждой из цифр от 0 до 9.

Подача изображения

и значения нейронов в последнем слое:

Другими словами, нейронная сеть к этому моменту «невероятно уверена», что это изображение — 4, и чтобы получить на выходе «4», нам просто нужно выбрать позицию с наибольшим значением.

Но что если мы посмотрим на предпоследний шаг? Самая последняя операция в сети — это так называемый softmax, который пытается «принудить к определённости». Но до него значения нейронов таковы:

Нейрон, представляющий «4», по‑прежнему имеет наибольшее числовое значение. Но есть информация и в значениях других нейронов. Мы можем ожидать, что этот список чисел в некотором смысле может быть использован для характеристики «сущности» изображения — и, таким образом, для получения чего‑то, что мы можем использовать в качестве эмбеддинга. Например, каждая из 4 здесь имеет немного другую «подпись» (или «эмбеддинг признаков») — но все они очень сильно отличаются от 8:

Пока мы использовали 10 чисел для характеристики наших изображений. Но зачастую лучше взять гораздо больше. Например, в нашей сети распознавания цифр мы можем получить массив из 500 чисел, обратившись к предыдущему слою. И это более‑менее реальный массив для использования в качестве «эмбеддинга образа».

Если мы хотим сделать явную визуализацию «пространства изображений» для рукописных цифр, нам нужно «уменьшить размерность», эффективно спроецировав полученный 500-мерный вектор, скажем, в трёхмерное пространство:

Мы только что описали создание характеристики (и, следовательно, эмбеддинга) для изображений. Сделали это с помощью эффективного определения сходства изображений путём определения того, соответствуют ли они одной и той же рукописной цифре. И мы можем поступить аналогично для большего количества образов, если у нас есть обучающий набор, который определяет какой из 5000 распространённых типов объектов (кошка, собака, стул,...) представляет собой каждое изображение. И таким образом мы можем сделать эмбеддинг изображения, которое «привязано» к нашей идентификации общих объектов, но затем «обобщается вокруг этого» в соответствии с поведением нейронной сети. Из‑за того, что этот механизм отчасти повторяет поведение людей при восприятии и интерпретации изображения, в конечном итоге это будет эмбеддинг, который «кажется нам правильным» и полезным на практике при выполнении «человекоподобных» задач.

Хорошо, но как же нам следовать такому же подходу для поиска эмбеддингов для слов? Начнём с тех, для которых мы можем легко провести обучение. Обычно такой задачей является «предсказание слов». Представьте, что нам дано слово «кот ___ ». На базе большого объёма текстов (скажем, текстового содержимого Интернета), каковы вероятности для различных слов, которые могут «заполнить пробел»? Или, в качестве альтернативы, для предложения «___ черный ___», каковы вероятности подстановки подходящих слов?

Как описать эту задачу нейронной сети? Мы должны сформулировать всё в числах. Один из способов — присвоить уникальный номер каждому из 50 000 или около того распространённых слов в английском языке. Так, например, «the» может быть 914, а «cat» (с пробелом перед ним) — 3542. (И это реальные числа, используемые GPT-2). Таким образом, для задачи «the ___ cat» наш входной сигнал может быть {914, 3542}. Каким должен быть выходной результат? Ну, это должен быть список из 50 000 или около того чисел, которые эффективно дают вероятности для каждого из возможных подстановок слов. И снова, чтобы найти эмбеддинги, мы хотим «перехватить» состояние нейронной сети непосредственно перед тем, как она «достигнет своего вывода», а затем подобрать список чисел, которые там встречаются и которые, как мы думаем, «характеризуют каждое слово».

Хорошо, так как же выглядят эти характеристики? За последние 10 лет была разработана целая серия различных систем (word2vec, GloVe, BERT, GPT, ...), каждая из которых основана на различных нейросетевых подходах. Но в конечном итоге все они берут слова и характеризуют их списками из сотен и тысяч чисел.

В необработанном виде эти «векторы эмбеддинга» довольно неинформативны. Например, вот что GPT-2 выдает в качестве сырых данных для трёх конкретных слов:

Если мы будем измерять расстояния между этими векторами, то сможем описать «близость» слов. Позже мы обсудим более подробно то, что можем считать «когнитивным» значением таких эмбеддингов. Но сейчас главное, что у нас есть способ полезно превратить слова в «удобные для нейронных сетей» наборы чисел.

На самом деле мы можем пойти дальше, чем просто характеризовать слова вектором; мы также можем делать это для последовательностей слов или целых блоков текста. И ChatGPT именно так и поступает. Он берёт текст и генерирует вектор эмбеддинга для его представления. Затем находит вероятности для различных слов, которые могут встретиться дальше. И он представляет свой ответ в виде списка чисел, которые в основном дают вероятность для каждого из 50 000 или около того возможных слов.

(Строго говоря, ChatGPT работает не со словами, а с «токенами» — удобными языковыми единицами, которые могут быть как целым словом, так и просто частью, такой как «pre», «ing» или «ized». Работа с лексемами облегчает ChatGPT работу с редкими, составными и неанглийскими словами, а иногда — хорошо это или плохо — позволяет изобретать новые).

Внутри ChatGPT

Итак, мы наконец‑то готовы обсудить, что же находится внутри ChatGPT. И да, в конечном итоге это гигантская нейронная сеть — в настоящее время это версия так называемой сети GPT-3 со 175 миллиардами весов. Во многих отношениях эта нейронная сеть очень похожа на другие, которые мы уже обсуждали. Но она специально создана для работы с текстом. И её наиболее примечательной особенностью является часть архитектуры, называемая «трансформером».

В первых нейронных сетях, которые мы обсуждали выше, каждый нейрон на любом слое был в основном связан с каждым нейроном на предыдущем слое. Но такая полностью связанная сеть (предположительно) является излишеством при работе с данными, имеющими определённую, известную структуру. Поэтому, например, на ранних стадиях работы с изображениями обычно используются так называемые конволюционные нейронные сети («конвнеты»), в которых нейроны располагаются на сетке, аналогичной пикселям изображения, и связаны только с нейронами, расположенными рядом.

Идея трансформеров заключается в том, чтобы сделать нечто похожее для последовательностей лексем, составляющих фрагмент текста. Но вместо того, чтобы просто определять фиксированную область в последовательности, между которой могут быть связи, трансформеры вводят понятие «внимания», т. е. идею «уделять внимание» некоторым частям последовательности больше, чем другим. Возможно, когда‑нибудь будет иметь смысл просто запускать общую нейронную сеть и настраивать её в процессе обучения. Но на данный момент на практике кажется критически важным «модулировать» вещи — как это делают трансформеры, и, вероятно, как это делает наш мозг.

Хорошо, так что же на самом деле делает ChatGPT (или, скорее, сеть GPT-3, на которой она основана)? Напомним, что её общая цель — продолжить текст «разумным» образом, основываясь на том, что она увидела в результате обучения (которое заключалось в просмотре миллиардов страниц текста из Интернета и т. д.) Таким образом, в любой момент времени у неё есть определённое количество текста, и её цель — придумать подходящий вариант для добавления следующего маркера.

ChatGPT работает в три основных этапа. Во‑первых, он берёт последовательность лексем, соответствующую тексту, и находит эмбеддинг (т. е. массив чисел), которое их представляет. Затем он обрабатывает этот эмбеддинг «стандартным для нейронных сетей способом», когда значения «просачиваются» через последовательные слои сети, чтобы создать новый эмбеддинг (т. е. новый массив чисел). Затем он берёт последнюю часть этого массива и генерирует из неё массив из примерно 50 000 значений, которые превращаются в вероятности для различных возможных следующих лексем. (И да, так получилось, что использовано примерно столько же лексем, сколько обычных слов в английском языке, хотя только около 3000 лексем являются целыми словами, а остальные — фрагментами).

Важным моментом является то, что каждая часть этого конвейера реализована нейронной сетью, веса которой определяются путем сквозного обучения сети. Другими словами, фактически ничто, кроме общей архитектуры, не является «явно спроектированным»; всё просто «обучается» на основе входных данных.

Однако в том, как устроена архитектура, есть множество деталей, отражающих всевозможный опыт и историй о нейронных сетях. И — хотя это замусоривает повествование — я думаю, что полезно поговорить о некоторых из этих деталей, не в последнюю очередь для того, чтобы получить представление о том, как создавался ChatGPT.

Сначала идёт модуль эмбеддингов. Вот его схематическое представление на языке Wolfram Language для GPT-2:

На вход подаётся вектор из n лексем (представленных, как и в предыдущем разделе, целыми числами от 1 до примерно 50 000). Каждая из этих лексем преобразуется однослойной нейронной сетью в вектор эмбеддинга (длиной 768 для GPT-2 и 12 288 для GPT-3 ChatGPT). Между тем, существует «вторичный путь», который принимает последовательность целочисленных позиций для лексем, и из этих целых чисел создаёт еще один вектор эмбеддинга. И, наконец, оба вектора — из значения и позиции — складываются вместе, чтобы получить конечную последовательность векторов эмбеддинга из этого модуля.

Почему нужно просто сложить вместе векторы эмбеддингов лексемы‑значения и лексемы‑позиции? Я не думаю, что этому есть какое‑то научное обоснование. Просто были испробованы различные способы, и этот способ, похоже, работает. И это часть мифов о нейронных сетях, что в некотором смысле можно докопаться до деталей, просто проведя достаточное обучение, без необходимости «понимать на инженерном уровне», как именно нейронная сеть в итоге настроила себя.

Вот результат работы модуля эмбеддинга для строки hello hello hello hello hello hello hello hello hello hello bye bye bye bye bye bye bye bye bye bye:

Элементы вектора эмбеддинга для каждой лексемы показаны внизу страницы, а поперек страницы мы видим сначала ряд эмбеддингов «hello», а затем ряд эмбеддингов «bye». Второй массив сверху — это позиционный эмбеддинг, его несколько случайная структура — это просто то, что «случайно было выучено» (в данном случае в GPT-2).

Итак, после модуля эмбеддинга наступает «главное событие» трансформера: последовательность так называемых «блоков внимания» (12 для GPT-2, 96 для GPT-3 компании ChatGPT). Всё это довольно сложно и напоминает типичные большие трудные для понимания инженерные системы, или, если уж на то пошло, биологические системы. Но в любом случае, вот схематическое изображение одного «блока внимания» (для GPT-2):

Внутри каждого такого блока внимания есть набор «руководителей» (12 для GPT-2, 96 для GPT-3 от ChatGPT) — каждый из которых независимо работает с разными частями значений в векторе эмбеддинга. (И, да, мы не знаем никаких конкретных причин, почему это хорошая идея — разделить вектор эмбеддинга, или что различные его части «означают»; это просто работает).

Хорошо, так что же делают эти руководители? По сути, это способ «оглянуться назад» в последовательности лексем (т. е. в тексте, созданном на данный момент) и «упаковать прошлое» в форму, полезную для поиска следующей лексемы. В первом разделе мы говорили об использовании вероятностей 2-грамм для отбора слов на основе их непосредственных предшественников. Механизм «внимания» в трансформерах позволяет «обращать внимание» даже на гораздо более ранние слова — таким образом, потенциально можно уловить, как глаголы могут ссылаться на существительные, которые появляются в предложении за много слов до них.

На более детальном уровне то, что делает руководитель, — это рекомбинирование фрагментов в векторах эмбеддинга, связанных с различными лексемами, с определенными весами. И так, например, 12 руководителей в первом блоке внимания (в GPT-2) имеют следующие («посмотрите назад по всему пути к началу последовательности токенов») шаблоны «весов рекомбинации» для строки «hello, bye» выше:

После обработки руководителями, полученный «перевзвешенный вектор эмбеддинга» (длиной 768 для GPT-2 и 12 288 для GPT-3/ChatGPT) пропускается через стандартный слой «полностью подключённой» нейронной сети. Трудно понять, что он делает, но вот график матрицы весов 768×768, которую он использует (здесь для GPT-2):

Если взять скользящие средние 64×64, то начинает вырисовываться некоторая структура (похожая на случайные колебания):

Что определяет эту структуру? В конечном итоге таково представление «нейросетевого кодирования» особенностей человеческого языка. Но что это могут быть за особенности, пока неизвестно. По сути, мы «открываем мозг ChatGPT» (или, по крайней мере, GPT-2) и обнаруживаем, что да, там всё сложно, и мы не понимаем этого — хотя он и воспроизводит понятные людям предложения.

Итак, пройдя через один блок внимания, мы получаем новый вектор эмбеддинга, который затем последовательно проходит через дополнительные (всего 12 для GPT-2; 96 для GPT-3). Каждый из них имеет свой собственный шаблон «внимания» и «полностью подключённых» весов. Здесь для GPT-2 приведена последовательность весов внимания для входа «hello, bye», для первого блока:

А вот (усредненные по перемещению) «матрицы» для полностью связанных слоев:

Любопытно, что хотя эти «матрицы весов» в разных блоках внимания выглядят довольно похоже, распределения величин весов могут несколько отличаться (и не всегда являются гауссовыми):

Итак, после прохождения через все эти блоки внимания каков чистый эффект трансформера? По сути, это преобразование исходной коллекции эмбеддингов для последовательности лексем в конечную коллекцию. А конкретный способ работы ChatGPT заключается в том, чтобы подобрать последний эмбеддинг в этой коллекции и «декодировать» его для получения списка вероятностей того, какая лексема должна быть следующей.

Вот в общих чертах то, что находится внутри ChatGPT. Он может показаться сложным (не в последнюю очередь из‑за множества неизбежных и несколько произвольных «инженерных решений»), но на самом деле его базовые элементы удивительно просты. Ведь мы имеем дело с нейронной сетью, состоящей из «искусственных нейронов», каждый из которых выполняет простую операцию — принимает набор числовых аргументов и затем комбинирует их с определенными весами.

Исходным входным сигналом для ChatGPT является массив чисел (векторы эмбеддингов для лексем на данный момент), и при создании следующей ChatGPT «запускает» их «пульсируют» по слоям нейронной сети, при этом каждый нейрон «делает своё дело» и передает результат нейронам следующего слоя. Нет никакого зацикливания или «возвращения назад». Всё просто «передается вперёд» через сеть.

Это очень отличается от типичной вычислительной системы, такой как машина Тьюринга, в которой результаты многократно «перерабатываются» одними и теми же вычислительными элементами. Здесь — по крайней мере, при генерации данного маркера выхода — каждый вычислительный элемент (т. е. нейрон) используется только один раз.

Но даже в ChatGPT в некотором смысле всё ещё существует «внешний цикл», который повторно использует вычислительные элементы. Потому что когда ChatGPT собирается генерировать новый токен, он всегда «читает» (т. е. берёт на вход) всю последовательность токенов, которые пришли до него, включая те, которые ChatGPT сам «написал» ранее. И мы можем считать, что эта установка означает, что ChatGPT действительно — по крайней мере, на самом внешнем уровне — включает в себя «цикл обратной связи», хоть в нём каждая итерация и представлена явно лексемой, которая появляется в им же сгенерированном тексте.

Но давайте вернёмся к сути ChatGPT: нейронной сети, которая многократно используется для генерации каждого токена. На каком‑то уровне она очень проста: целая коллекция одинаковых искусственных нейронов. Некоторые части сети состоят из слоёв нейронов, в которых каждый нейрон на одном слое связан (с некоторым весом) с каждым нейроном на предыдущем. Но благодаря в том числе и своей трансформерской архитектуре, ChatGPT имеет части с большей структурой, в которых подключены только определённые нейроны на разных слоях. (Можно сказать, что «все нейроны связаны», но некоторые из них имеют нулевой вес).

Кроме того, в ChatGPT есть нюансы, которые говорят о том, что нейронка состоит из не совсем однородных слоёв. Например, как показано в приведённом выше кратком обзоре, внутри блока внимания есть места, где создаётся несколько копий входных данных, каждая из которых затем проходит через различные «пути обработки», потенциально включающие разное количество слоёв, и лишь затем рекомбинируется. Но хотя это может быть удобным представлением происходящего, всегда можно думать о «плотном заполнении» слоёв, но при этом некоторые веса должны быть нулевыми.

Если посмотреть на самый длинный путь данных через ChatGPT, то в нём задействовано около 400 основных слоёв — в некотором смысле это не так уж и много. Но это миллионы нейронов — в общей сложности 175 миллиардов связей и, следовательно, 175 миллиардов весов. И нужно понимать, что для каждого нового токена ChatGPT делает вычисления над всеми ними. На практике эти вычисления могут быть разбиты «по слоям» в высокопараллельные массивы операций, которые удобно выполнять на GPU. Но на каждый создаваемый токен всё равно приходится 175 миллиардов вычислений (а в конечном итоге — ещё больше) — неудивительно, что на генерацию длинного текста у ChatGPT может уйти немало времени.

Но, в конце концов, замечательно, что все эти операции — по отдельности такие простые, как они есть — могут каким‑то образом вместе сделать такую хорошую «человекоподобную» работу по созданию текста. Следует ещё раз подчеркнуть, что на текущий момент нет никакой «финальной теории», почему что‑то подобное должно работать. И на самом деле, как мы ещё обсудим, я думаю, что мы должны рассматривать это как потенциально удивительное научное открытие: что каким‑то образом в нейронной сети, подобной ChatGPT, можно уловить суть работы человеческого мозга при чтении или письме.

Обучение ChatGPT

Итак, мы в общих чертах рассказали о том, как работает ChatGPT. Но как он был создан? Как были определены все эти 175 миллиардов весов в нейронной сети? По сути, они являются результатом очень масштабного обучения, основанного на огромном объёме текстов в Интернете, в книгах и т. д., написанных людьми. Как мы уже говорили, даже учитывая все эти обучающие данные, не очевидно, что нейронная сеть сможет успешно создавать «человекоподобный» текст. И похоже, что для этого необходимы дополнительные инженерные разработки. Но главный сюрприз и открытие ChatGPT как явления заключается в том, что это вообще возможно. Вдумайтесь — нейронная сеть с «всего лишь» 175 миллиардами весов может создать «разумную модель» текста, написанного человеком.

В наше время существует множество оцифрованных текстов, которые были написанных людьми. В общедоступном Интернете есть по меньшей мере несколько миллиардов страниц, что составляет в общей сложности, возможно, триллион слов текста. А если включить сюда и непубличные веб‑страницы, то это число может быть как минимум в 100 раз больше. На сегодняшний день доступно более 5 миллионов оцифрованных книг (из 100 миллионов когда‑либо опубликованных), что даёт ещё около 100 миллиардов слов. И это ещё не считая текста, полученного из речи в видео и т. д. (Для сравнения: за всю мою жизнь я опубликовал чуть меньше 3 миллионов слов, а за последние 30 лет я написал около 15 миллионов слов по электронной почте и набрал в общей сложности около 50 миллионов слов. Но всего за последние пару лет я произнёс более 10 миллионов слов на публичных выступлениях. И да, я обучу бота всему этому).

И учитывая все эти данные, как обучить нейронную сеть? Базовый процесс очень похож на тот, который мы обсуждали в простых примерах выше. Вы предоставляете кучу примеров, а затем настраиваете веса в сети, чтобы минимизировать ошибку («потери»), которую она делает на этой выборке. Основная сложность в «обратном распространении» ошибки, что каждый раз, когда она всплывает, каждый вес в сети, как правило, изменяется хотя бы немного, и приходится иметь дело с большим количеством весов. (Фактические «обратные вычисления» обычно лишь на небольшую величину сложнее, чем прямые).

С помощью современного GPU можно легко параллельно вычислять результаты, полученные из тысяч примеров. Но когда дело доходит до фактического обновления весов в нейронной сети, существующие методы требуют делать это практически батчами. (И да, возможно, именно здесь настоящий мозг с его объединёнными элементами вычислений и памяти имеет архитектурное преимущество).

Даже в простых случаях обучения числовых функций, которые мы обсуждали ранее, для успешного обучения сети с нуля, нам часто приходилось использовать миллионы примеров. Так сколько же данных нам понадобится для обучения модели «человекоподобного языка»? Кажется, нет никакого фундаментального «теоретического» способа узнать это. Но на практике ChatGPT была успешно обучена на нескольких сотнях миллиардов слов текста.

Часть текстов ему подавали несколько раз, часть — только один. Но каким‑то образом он получил то, что ему нужно из увиденного. Учитывая этот объём, какого размера сеть должна быть, чтобы «хорошо его выучить»? Опять же, у нас пока нет фундаментального теоретического способа ответить на этот вопрос. Предполагается, что существует определённое «общее алгоритмическое содержание» человеческого языка и того, как люди с его помощью общаются. Но вопрос в том, насколько эффективно нейронная сеть будет реализовывать модель, основанную на этом алгоритмическом содержании. И снова мы не знаем — хотя успех ChatGPT позволяет предположить, что она достаточно эффективна.

Давайте просто отметим, что ChatGPT работает, используя пару сотен миллиардов весов — сравнимых по количеству с общим количеством слов (или токенов) обучающих данных, которые ему были предоставлены. В некотором смысле удивительно (хотя эмпирически это наблюдается и в меньших аналогах ChatGPT), что «размер сети», которая хорошо работает, настолько сопоставим с размером обучающих данных. Ведь дело, конечно, не в том, что каким‑то образом внутри ChatGPT напрямую хранится весь этот текст из Интернета, книг и так далее. Потому что на самом деле внутри ChatGPT находится куча чисел с точностью чуть меньше 10 знаков, которые являются своего рода распределённым кодированием совокупной структуры всего этого текста.

Иными словами, мы можем спросить, каково «эффективное информационное содержание» человеческого языка и как оно обычно используется. В начале есть сырые примеры текстов. А затем есть представление в нейронной сети ChatGPT. Это представление, скорее всего, далеко от «алгоритмически минимального» (о чем мы поговорим ниже), но оно может быть легко использовано нейронной сетью. Там, похоже, происходит довольно незначительное «сжатие» обучающих данных. В среднем кажется, что для переноса «информационного содержания» одного слова обучающих данных требуется чуть меньше одного веса нейронной сети.

Когда мы запускаем ChatGPT для генерации текста, нам приходится использовать каждый вес один раз. Таким образом, если есть n весов, то нам нужно выполнить порядка n вычислительных шагов — хотя на практике многие из них обычно могут выполняться параллельно на GPU. Но если для установки этих весов нам потребуется около n слов обучающих данных, то из сказанного выше можно сделать вывод, что для обучения сети нам потребуется около n^2 вычислительных шагов — вот почему при использовании современных методов приходится говорить о миллиардных затратах на обучение.

За пределами базовой подготовки

Большая часть усилий по обучению ChatGPT тратится на то, чтобы показать ему огромный объём существующих текстов из Интернета, книг и т. д. Но оказалось, что есть и другая, по‑видимому, довольно важная часть.

Как только нейронная сеть внутри ChatGPT завершает своё «сырое обучение» на предоставленном объёме текстов, она готова начать генерировать собственный текст, продолжая его по подсказкам и т. д. Но хотя результаты, полученные таким образом, часто кажутся разумными, они имеют тенденцию — особенно для длинных кусков текста — «блуждать», часто довольно нечеловеческими способами. Это не так просто обнаружить с помощью традиционного статистического анализа текста, но человек заметит это с лёгкостью.

Ключевой идеей при создании ChatGPT было сделать ещё один шаг после «пассивного чтения» веба и книг: чтобы реальные люди активно взаимодействовали с ChatGPT, видели, что он производит, и фактически давали ему обратную связь о том, «как стать хорошим чатботом». Но как нейронная сеть может использовать эту обратную связь? На первом этапе люди просто оценивают результаты работы нейросети. Но затем строится другая нейросетевая модель, которая пытается предсказать эти оценки. Но теперь эта модель предсказания может быть запущена — по сути, как функция потерь — на исходной сети, что позволяет «настроить» эту сеть с помощью обратной связи, полученной от людей. И результаты на практике, похоже, оказывают большое влияние на успех системы в создании «человекоподобного» результата.

Интересно, как сильно нужно «подталкивать» первоначально обученную сеть, чтобы заставить её развиваться в правильном направлении. Можно было бы представить эти правки как будто она «узнала что‑то новое», а затем перезапустить алгоритм обучения, корректируя веса и так далее.

Но это не так. Вместо этого, похоже, достаточно сказать ChatGPT что‑то один раз — как часть подсказки, которую вы даёте — и затем он может успешно использовать эти знания, когда генерирует текст. Тот факт, что это работает, является важным ключом к пониманию того, что ChatGPT «на самом деле делает» и как это связано со структурой языка и мышления.

В этом есть что‑то человеческое: после предварительного обучения вы можете сказать ему что‑то всего один раз, и он может «запомнить это» — по крайней мере, «достаточно долго», чтобы эти знания были отражены в новом сгенерированном куске текста. Так что же происходит в таком случае? Может быть, «всё, что вы можете сказать ему, уже где‑то есть», и вы просто направляете его в правильную сторону? Но это не кажется правдоподобным. Вместо этого более вероятным кажется, что элементы уже есть, но специфика определяется чем‑то вроде «траектории между ними», и ваши исправления донастраивают их.

И действительно, как и для людей, если вы скажете ему что‑то странное и неожиданное, что совершенно не вписывается в известную ему картину мира, не похоже, что он сможет успешно «интегрировать» это. ChatGPT примет новую информацию во внимание только в том случае, если это накладывается довольно простым способом поверх уже имеющегося у него понимания мира.

Также стоит ещё раз отметить, что неизбежно существуют «алгоритмические пределы» того, что нейронная сеть может «воспринять». Скажите ей «неглубокие» правила вида «это приведёт к тому‑то» и т. д., и нейронная сеть, скорее всего, будет в состоянии представить и воспроизвести их с лёгкостью — и действительно, то, что она «уже знает» из языка, даст ей немедленный образец для подражания. Но попробуйте дать ей правила для настоящего «глубокого» вычисления, которое включает множество потенциально несводимых к вычислениям шагов, и это просто не сработает. (Помните, что на каждом шаге он всегда просто «подаёт данные вперед» в своей сети, никогда не зацикливаясь, кроме как в силу генерации новых лексем).

Конечно, сеть может знать ответ на конкретные «несводимые» вычисления. Но как только появится комбинаторное число возможностей, никакой такой подход в стиле «таблиц» не будет работать. И поэтому, да, как и людям, нейронным сетям пора «протянуть руку помощи» и использовать реальные вычислительные инструменты.

Что действительно позволяет ChatGPT работать?

Человеческий язык и процессы мышления всегда казались некой вершиной сложности. Удивительно, как человеческий мозг с его сетью из «всего лишь» 100 миллиардов нейронов (и, возможно, 100 триллионов связей) может быть ответственен за это. Возможно, в мозге есть нечто большее, чем сеть нейронов, например, какой‑то новый слой неизвестного действия. Но теперь, благодаря ChatGPT, мы получили новую важную информацию: мы знаем, что чистая искусственная нейронная сеть, имеющая примерно столько же связей, сколько нейронов в мозге, способна на удивление хорошо имитировать человеческий язык.

И да, это всё ещё большая и сложная система, в которой примерно столько же весов нейронной сети, сколько слов текста, доступных в настоящее время в мире. Но на каком‑то уровне трудно поверить, что всё богатство языка и вещей, о которых он может рассказать, может быть заключено в такую ограниченную систему. Отчасти происходящее является отражением повсеместного явления (которое впервые стало очевидным на примере правила 30), что вычислительные процессы могут значительно усилить кажущуюся сложность систем, даже если лежащие в их основе правила просты. Но на самом деле нейронные сети, используемые в ChatGPT, обычно специально строятся так, чтобы ограничить влияние этого явления и связанной с ним вычислительной несводимости в интересах повышения доступности их обучения.

Как же тогда получается, что что‑то вроде ChatGPT может зайти так далеко, как на примере с речью? Основной ответ, я думаю, заключается в том, что наш язык на фундаментальном уровне всё же проще, чем кажется. И это означает, что ChatGPT — даже с его в конечном счете простой структурой нейронной сети — успешно способен «уловить суть» человеческого разговора и мышления, лежащего в его основе. Более того, в процессе обучения ChatGPT каким‑то образом «неявно обнаружил» те закономерности в языке (и мышлении), которые делают это возможным.

Успех ChatGPT, как мне кажется, даёт нам доказательства фундаментальной и важной части науки: он говорит о том, что мы можем ожидать открытия новых важных «законов языка» — и фактически «законов мышления». В ChatGPT, построенном как нейронная сеть, эти законы в лучшем случае неявные. Но если мы сможем каким‑то образом сделать эти законы явными, то появится возможность делать те вещи, которые делает ChatGPT, гораздо более простыми, эффективными и прозрачными способами.

Какого рода могут быть эти законы? В конечном итоге они должны дать нам некий рецепт того, как язык и то, как мы говорим с его помощью, собираются вместе. Позже мы обсудим, как «взгляд изнутри ChatGPT» может дать нам некоторые подсказки об этом, и как идеи создания вычислительного языка, указывает нам путь вперёд. Но сначала давайте обсудим два давно известных примера того, что можно назвать «законами языка» — и как они связаны с работой ChatGPT.

Первое — это синтаксис языка. Язык — это не просто случайное нагромождение слов. Существуют определённые грамматические правила как слова разных типов могут быть собраны вместе. Например, в английском языке существительные могут предшествовать прилагательным и следовать за глаголами, но обычно два существительных не могут находиться рядом друг с другом. Такая грамматическая структура может быть отражена набором правил, которые позволяют строить «деревья разбора»:

ChatGPT не имеет явных «знаний» о таких правилах. Но каким‑то образом в процессе обучения он неявно обнаруживает их — и затем, похоже, хорошо им следует. Так как же это работает? На уровне «общей картины» это неясно. Но чтобы получить некоторое представление будет полезно рассмотреть более простой пример.

Рассмотрим «язык», сформированный из последовательностей ( и ), с грамматикой, определяющей, что скобки всегда должны быть сбалансированы, и представим в виде дерева разбора:

Можно ли обучить нейронную сеть создавать «грамматически правильные» последовательности скобок? Существуют различные способы обработки этого, но давайте воспользуемся сетями с трансформерами, как это делает ChatGPT. И если у нас есть такая простая сеть, мы можем начать скармливать ей грамматически правильные последовательности скобок в качестве обучающих примеров. Тонкость (которая на самом деле также проявляется в генерации человеческого языка ChatGPT) заключается в том, что в дополнение к нашим «маркерам содержания» (здесь «(» и «)») мы должны включить маркер «End», который генерируется для остановки работы сети (т. е. для ChatGPT, что человек достиг «конца истории»).

Если мы создадим сеть с одним блоком внимания с 8 руководителями и векторами признаков длиной 128 (ChatGPT также использует векторы признаков длиной 128, но имеет 96 блоков внимания, каждый из которых имеет 96 руководителей), то, кажется, невозможно заставить её узнать много нового о языке скобок. Но с 2 блоками внимания процесс обучения, похоже, сходится — по крайней мере, после предоставления 10 миллионов примеров (и, как это обычно бывает с трансформерными сетями, показ ещё большего количества примеров только ухудшает его производительность).

Таким образом, с помощью этой сети мы можем сделать аналог того, что делает ChatGPT, и запросить вероятности того, каким должен быть следующий токен в последовательности:

В первом случае сеть «почти уверена», что последовательность не может закончиться на этом фрагменте — что хорошо, потому что если бы это произошло, скобки остались бы несбалансированными. Во втором случае, однако, она «правильно распознает», что последовательность может закончиться, хотя она также «указывает», что можно «начать сначала», поставив «(«, предположительно с последующим „)“. Но даже с его 400 000 или около того кропотливо обученных весов, он говорит, что вероятность следующей лексемы „)“ составляет 15%, что неправильно, потому что это обязательно приведёт к несбалансированной скобке.

Вот что мы получим, если попросим сеть найти наиболее вероятные завершения для всё более длинных последовательностей:

И да, до определенной длины сеть работает отлично. Но потом она начинает сбоить. Это довольно типичное поведение, которое можно увидеть в «точной» ситуации, подобной этой, с нейронной сетью (или с машинным обучением в целом). Случаи, которые человек «решает с первого взгляда», нейросеть тоже может решить. Но случаи, требующие выполнения чего‑то «более алгоритмического» (например, явного подсчета скобок, чтобы проверить, закрыты ли они), нейросеть, как правило, оказывается «слишком вычислительно неглубокой». (Кстати, даже полный текущий ChatGPT с трудом справляется с корректным сопоставлением скобок в длинных последовательностях). Так что нейронка никогда не заменит lisp-программистов

Но как это относится к ChatGPT? Язык скобок является «строгим» — т. е. более «алгоритмическим». Но в английском гораздо больше шансов «угадать» что грамматически подходит на основе локального выбора слов и других подсказок. И да, нейронная сеть справляется с этим гораздо лучше — даже несмотря на то, что она может пропустить какой‑нибудь «формально правильный» случай, который, впрочем, может не заметить и человек. Но главное, что наличие общей синтаксической структуры языка со всеми вытекающими отсюда закономерностями в некотором смысле ограничивает «количество», которое нейросеть должна выучить. И ключевым «естественнонаучным» наблюдением является то, что трансформерная архитектура нейронных сетей, например, в ChatGPT, успешно справляется с изучением синтаксической структуры типа «вложенное дерево», которая, похоже, существует (хотя бы в некотором приближении) во всех человеческих языках.

Синтаксис обеспечивает один из видов ограничениё языковых конструкций. Но их явно больше. Такое предложение, как «Любознательные электроны едят голубые теории для рыбы», грамматически правильно, но это не то, что обычно хотят сказать, и не считалось бы успехом, если бы ChatGPT сгенерировал его — потому что оно, по сути, бессмысленно.

Но есть ли общий способ определить, является ли предложение осмысленным? Традиционной общей теории для этого не существует. Но можно считать, что ChatGPT неявно «разработал теорию для этого» после обучения на миллиардах предложений из Интернета и т. д.

Какой может быть эта теория? Есть одна такая штука, который известна уже два тысячелетия, и это логика. И, конечно, в форме силлогизма, в которой её открыл Аристотель, логика — это способ сказать, что предложения, которые следуют определённым шаблонам, разумны, а другие — нет. Так, например, разумно сказать: «Все X есть Y. Это не Y, поэтому это не X» (как в «Все рыбы синие. Это не синее, поэтому это не рыба»). И так же, как можно несколько причудливо представить, что Аристотель открыл силлогистическую логику, просматривая («в стиле машинного обучения») множество примеров риторики, так же можно представить, что при обучении ChatGPT он сможет «открыть силлогистическую логику», просматривая множество текстов в Интернете и т. п. (И да, хотя можно ожидать, что ChatGPT будет выдавать текст, содержащий «правильные умозаключения», основанные на таких вещах, как силлогистическая логика, это совсем другая история, когда дело доходит до более сложной формальной логики — и я думаю, что можно ожидать, что он потерпит неудачу здесь по тем же причинам, по которым он терпит неудачу в подборе скобок).

Но за пределами узкого примера логики, что можно сказать о том, как систематически конструировать (или распознавать) даже правдоподобно осмысленный текст? Да, есть такие вещи, как Mad Libs, которые используют очень специфические «шаблоны фраз». Но каким‑то образом ChatGPT неявно имеет гораздо более общий способ сделать это. И, возможно, нет ничего, что можно было бы сказать о том, как это можно сделать, кроме «это как‑то происходит, когда у вас 175 миллиардов весов нейронной сети». Но я наверняка уверен, что существует гораздо более простое и понятное объяснение.

Смысловое пространство и семантические законы движения

Выше мы говорили о том, что в ChatGPT любой фрагмент текста эффективно представлен массивом чисел, которые можно представить как координаты точки в некотором «пространстве лингвистических характеристик». Поэтому, когда ChatGPT продолжает фрагмент текста, это соответствует прослеживанию траектории в пространстве лингвистических признаков. Но теперь мы можем спросить, что заставляет эту траекторию соответствовать тексту, который мы считаем осмысленным. И, возможно, существуют некие «семантические законы движения», которые определяют — или ограничивают — как точки в пространстве лингвистических признаков могут перемещаться, сохраняя «осмысленность»?

Как же выглядит это пространство лингвистических характеристик? Вот пример из отдельных слов в проекции на плоскость:

Выше мы рассмотрели другой пример, основанный на словах, обозначающих растения и животных. Но в обоих случаях суть в том, что «семантически похожие слова» располагаются рядом.

В качестве другого примера, вот как располагаются слова, соответствующие различным частям речи:

Конечно, данное слово в общем случае не имеет единственного значения (или не обязательно соответствует только одной части речи). И, глядя на то, как предложения, содержащие слово, располагаются в пространстве признаков, часто можно «разобрать» различные значения — как в приведенном здесь примере со словом «crane» (птица или машина?):

Хорошо, по крайней мере правдоподобно, что мы можем думать об этом пространстве признаков как о размещении «слов, близких по значению» близко друг к другу. Но какую дополнительную структуру мы можем выявить? Существует ли, например, какое‑то понятие «параллельного переноса», которое отражало бы «плоскостность» пространства? Один из способов разобраться в этом — обратиться к аналогиям:

Мы можем посмотреть на траекторию, по которой подсказка для ChatGPT движется в пространстве характеристик, а затем увидеть, как ChatGPT продолжает её:

Здесь, конечно, нет «геометрически очевидного» закона движения. И это совсем не удивительно; найти его если и возиожно, то очень сложно. И, например, далеко не очевидно, что даже если и существует «семантический закон движения», то в каком вложении (или, по сути, в каких «переменных») он будет наиболее естественно выражен.

На рисунке выше мы показываем несколько шагов «траектории», где на каждом мы выбираем слово, которое ChatGPT считает наиболее вероятным (случай «нулевой температуры»). Но мы также можем спросить, какие слова могут быть «следующими» с какой вероятностью в данный момент:

И в данном случае видим, что существует «веер» высоковероятных слов, который, кажется, идёт в более или менее определённом направлении в пространстве признаков. Но что будет дальше? Вот последовательные «вееры», которые появляются по мере нашего «продвижения» по траектории:

Вот 3D‑представление, проходящее в общей сложности 40 шагов:

Выглдит такое движение беспорядочным — и никак не помогает в выявлении «математически‑физически‑подобных» «семантических законов движения» путём эмпирического изучения того, «что ChatGPT делает внутри». Но, возможно, мы просто смотрим на «неправильные переменные», и если бы сменили систему координат, то сразу бы увидели, что ChatGPT делает что‑то «математически‑физически простое» вроде следования геодезическим линиям. Но пока мы не готовы «эмпирически расшифровать» на основе «внутреннего поведения» ChatGPT то, как он понимает устройство человеческого языка.

Семантическая грамматика и сила вычислительного языка

Что нужно для создания «осмысленного человеческого языка»? В прошлом мы могли предположить, что это может быть не что иное, как человеческий мозг. Но теперь мы знаем, что это вполне по силам нейронной сети ChatGPT. Тем не менее, пока это всё, до чего мы дошли, и не будет ничего более простого или более понятного для человека, что могло бы сработать. Но я подозреваю, что успех ChatGPT косвенно раскрывает важный «научный» факт: на самом деле в осмысленном человеческом языке гораздо больше структуры и простоты, чем мы когда‑либо знали, и что в конечном итоге могут существовать даже довольно простые правила, описывающие, как такой язык может быть составлен.

Как мы уже говорили, синтаксическая грамматика даёт правила того, как слова, соответствующие различным частям речи, могут быть собраны вместе в человеческом языке. Но чтобы разобраться со значением, нам нужно копнуть глубже. И одно из направлений — думать не только о синтаксической грамматике языка, но и о семантической.

Для целей синтаксиса мы определяем такие вещи, как существительные и глаголы. Но для целей семантики нам нужны «более тонкие градации». Так, например, мы можем определить понятие «перемещение» и понятие «объект», который «сохраняет свою идентичность независимо от местоположения». Существует бесконечное множество конкретных примеров каждого из этих «семантических понятий». Но для целей нашей семантической грамматики мы просто будем иметь некое общее правило, которое в основном говорит, что «объекты» могут «двигаться». Можно многое сказать о том, как всё это может работать (кое‑что я уже упомянул ранее). Но здесь я ограничусь лишь несколькими замечаниями, которые указывают на некоторые потенциальные пути развития.

Стоит отметить, что даже если предложение правильно составлено согласно семантической грамматике, это не означает, что оно было реализовано (или даже может быть реализовано) на практике. «Слон путешествовал на Луну», несомненно, «пройдёт» нашу семантическую грамматику, но оно определенно не было реализовано в нашем реальном мире — хотя для вымышленного мира это абсолютно возможно.

Когда мы начинаем говорить о «семантической грамматике», то вскоре задаёмся вопросом: «Что под ней скрывается?». Какую «модель мира» она предполагает? Синтаксическая грамматика — это действительно просто построение языка из слов. Но семантическая грамматика обязательно имеет дело с некой «моделью мира» — чем‑то, что служит «скелетом», на который может быть нарощен язык, созданный из реальных слов.

До недавнего времени мы могли предполагать, что (человеческий) язык будет единственным общим способом описания нашей модели мира. Уже несколько веков назад начали появляться формализации конкретных видов вещей, основанные, в частности, на математике. Но сейчас существует гораздо более общий подход к формализации: вычислительный язык.

И да, это был мой большой проект на протяжении более чем четырех десятилетий (который теперь воплощён в языке Wolfram Language): разработать точное символическое представление, которое может говорить как можно шире о вещах в мире, а также об абстрактных вещах, которые нас интересуют. Так, например, у нас есть символьные представления для городов, молекул, изображений и нейронных сетей, и у нас есть встроенные знания о том, как вычислять эти вещи.

И, после десятилетий работы, мы охватили таким образом множество областей. Но в прошлом мы не особенно занимались «повседневным дискурсом». В фразе «Я купил два фунта яблок» мы можем легко представить (и выполнить вычисления по питанию и другие вычисления) «два фунта яблок». Но у нас нет (пока) символического представления для «я купил».

Всё это связано с идеей семантической грамматики — целью иметь общий символический «строительный набор» для понятий, который дал бы нам правила сочетания с чем, и, таким образом, для «потока» того, что мы можем превратить в человеческий язык.

Но, допустим, у нас есть этот «язык символического дискурса». Что бы мы с ним делали? Для начала — заняться созданием «локально осмысленного текста». Но в конечном итоге мы, скорее всего, захотим получить более «глобально значимые» результаты — что означает «вычислять» больше о том, что может реально существовать или происходить в мире (даже, вполне возможно, и вымышленном).

Сейчас в Wolfram Language у нас есть огромное количество встроенных вычислительных знаний о множестве видов вещей. Но для полноценного языка символического дискурса нам пришлось бы встроить дополнительные «вычисления» об общих вещах в мире: если объект перемещается из A в B и из B в C, то он переместился из A в C и т. д.

Имея язык символического дискурса, мы можем использовать его для создания «самостоятельных высказываний». Но мы также можем использовать его, чтобы задавать вопросы о мире в стиле «Wolfram|Alpha». Или мы можем использовать его для утверждения вещей, которые мы «хотим сделать таковыми», предположительно с помощью какого‑то внешнего механизма приведения в действие. Или мы можем использовать его, чтобы делать утверждения — возможно, о реальном мире, а возможно, о каком‑то конкретном мире, который мы рассматриваем, вымышленном или ином.

Человеческий язык принципиально неточен, не в последнюю очередь потому, что он не «привязан» к конкретной вычислительной реализации, и его значение в основном определяется только «общественным договором» между его пользователями. Но вычислительный язык, по своей природе, имеет определенную фундаментальную точность — потому что в конечном итоге то, что он определяет, всегда может быть «однозначно выполнено на компьютере». Человеческий язык обычно может обойтись без некоторой расплывчатости. (Когда мы говорим «планета», включает ли она экзопланеты или нет и т. д.?) Но в вычислительном языке мы должны быть точны и ясны во всех употребляемых терминах.

Часто удобно использовать обычный человеческий язык для придумывания имён в вычислительном языке. Но значения, которые они там имеют, обязательно точны и могут нести в том числе и некоторую коннотацию.

Как определить фундаментальную «онтологию», подходящую для общего языка символического дискурса? Ну, это нелегко. Возможно, именно поэтому в этой области мало что было сделано со времен примитивных начинаний Аристотеля более двух тысячелетий назад. Но очень помогает наше умение и понимание как думать о мире вычислительно (и не помешает «фундаментальная метафизика» из нашего проекта «Физика» и идея рулиады).

Но что всё это значит в контексте ChatGPT? В процессе обучения он эффективно «собрал воедино» определённое (довольно впечатляющее) количество того, что составляет семантическую грамматику. Но сам его успех даёт нам основание думать, что можно построить нечто более полное в форме вычислительного языка. И, в отличие от того, что мы пока выяснили о внутренностях ChatGPT, мы можем рассчитывать на разработку такого вычислительного языка, который был бы понятен человеку.

Говоря о семантической грамматике, мы можем провести аналогию с силлогистической логикой. Сначала силлогистическая логика была, по сути, набором правил относительно высказываний, выраженных на человеческом языке. Но (да, два тысячелетия спустя), когда была разработана формальная логика, первоначальные базовые конструкции силлогистической логики теперь можно было использовать для построения огромных «формальных башен», включающих, например, работу современных цифровых схем. И так, мы можем ожидать, будет с более общей семантической грамматикой. Сначала она будет способна работать только с простыми шаблонами, выраженными, скажем, в виде текста. Но когда будет создан весь каркас вычислительного языка, можно ожидать, что он сможет использоваться для возведения высоких башен «обобщенной семантической логики», которые позволят нам работать точным и формальным образом со всеми видами вещей, которые никогда не были доступны нам раньше, разве что только на «уровне первого этажа» через человеческий язык со всей его неясностью.

Мы можем думать о построении вычислительного языка и семантической грамматики как о своего рода предельном сжатии в представлении вещей. Потому что она позволяет нам говорить о сути возможного, не имея, например, дело со всеми «оборотами речи», которые существуют в обычном человеческом языке. И мы можем рассматривать большую силу ChatGPT как нечто подобное: потому что он тоже в некотором смысле «просверлил» до такой степени, что может «собрать язык вместе семантически значимым образом», не заботясь о различных возможных оборотах речи.

Что же произойдёт, если мы применим ChatGPT к базовому вычислительному языку? Вычислительный язык может описать то, что возможно. Но всё ещё можно добавить ощущение «того, что популярно», основанное, например, на чтении всего этого контента в Интернете. Но затем работа с вычислительным языком означает, что что‑то вроде ChatGPT имеет немедленный и фундаментальный доступ к тому, что равнозначно окончательным инструментам для использования потенциально несводимых вычислений. И это делает его системой, которая может не только «генерировать разумный текст», но и рассчитывать на то, что она сможет определять действительно ли этот текст делает «правильные» заявления о мире — о чём бы он не был.

Итак... Что делает ChatGPT, и почему он работает?

Основная концепция ChatGPT на определённом уровне довольно проста. Начните с огромной выборки созданного человеком текста из Интернета, книг и т. д. Затем обучите нейронную сеть генерировать текст, который «похож на этот». И, в частности, сделать так, чтобы она могла начать с «подсказки», а затем продолжить текст, который «похож на то, чему она была обучена».

Как мы уже видели, нейронная сеть в ChatGPT состоит из очень простых элементов — хотя их миллиарды. И основная работа нейронной сети также очень проста и заключается в том, что она пропускает входные данные, полученные из текста, который она сгенерировала до сих пор, «один раз через свои элементы» (без каких‑либо циклов и т. д.) для каждого нового слова (или части слова), которое она генерирует.

Но самое замечательное и неожиданное заключается в том, что этот процесс может производить текст, который определённо похож на тот, что есть в Интернете, в книгах и т. д.. И это не только связный человеческий язык, он также «что‑то говорит» следуя подсказкам и используя тексты, которое он «прочитал». Он не всегда говорит вещи, которые «глобально имеют смысл» (или соответствуют правильным вычислениям) — потому что он просто подбирает слова, которые «звучат правильно», основываясь на том, как они «звучали» в его учебном материале.

Специфическая инженерия ChatGPT сделала его весьма убедительным. Но в конечном итоге (по крайней мере, пока он не сможет использовать внешние инструменты) ChatGPT «всего лишь» вытягивает некую «связную нить текста» из накопленной им «статистики общепринятой мудрости». Но удивительно, насколько результаты похожи на человеческие. И, как я уже говорил, это позволяет предположить нечто очень важное с научной точки зрения: человеческий язык (и модели мышления, лежащие в его основе) как‑то проще и более «законоподобны» в своей структуре, чем мы думали. ChatGPT косвенно подтверждает это. Но в дальнейшем, теоретически, мы можем раскрыть это явно, с помощью семантической грамматики, вычислительного языка и т. д.

То, что делает ChatGPT в плане генерации текста, очень впечатляет — и результаты обычно очень похожи на то, что могли бы произвести мы, люди. Значит ли это, что ChatGPT работает как мозг? Структура искусственной нейросети, лежащая в его основе, в конечном итоге была смоделирована на основе идеализации мозга. И кажется вполне вероятным, что когда мы, люди, генерируем язык, многие аспекты происходящего очень похожи.

Когда дело доходит до обучения (AKA learning), различное «оборудование» мозга и современных компьютеров (а также, возможно, некоторые неразработанные алгоритмические идеи) заставляет ChatGPT использовать стратегию, которая довольно сильно отличается (и в некоторых отношениях гораздо менее эффективна), чем у мозга. И ещё кое‑что: в отличие даже от типичных алгоритмических вычислений, ChatGPT не имеет внутренних «циклов» или «повторных вычислений из исходных данных». И это неизбежно ограничивает его вычислительные возможности — даже по отношению к современным компьютерам, что уж говорить про мозг.

Неясно, как «исправить это» и сохранить возможность обучать систему с разумной эффективностью. Но, предположительно, это позволит будущему ChatGPT делать ещё больше «мозгоподобных вещей». Конечно, есть много вещей, которые мозг делает не так хорошо — в частности, связанных с несводимыми вычислениями. И для них и мозгу, и таким вещам, как ChatGPT, приходится искать «внешние инструменты» — например, Wolfram Language.

Но пока интересно посмотреть, что уже удалось сделать ChatGPT. На каком‑то уровне это отличный пример фундаментального научного факта, что большое количество простых вычислительных элементов может делать удивительные и неожиданные вещи. Но это также даёт, возможно, лучший за последние две тысячи лет импульс для лучшего понимания фундаментального характера и принципов той центральной черты человеческого бытия, которой является человеческий язык и стоящие за ним процессы мышления.

Спасибо

Я слежу за развитием нейронных сетей уже около 43 лет, и за это время я общался со многими людьми на эту тему. Среди них — некоторые давно, некоторые недавно, а некоторые на протяжении многих лет — были: Джулио Алессандрини, Дарио Амодей, Этьен Бернар, Талиесин Бейнон, Себастьян Боденштейн, Грег Брокман, Джек Коуэн, Педро Домингос, Джесси Галеф, Роджер Гермундссон, Роберт Хехт‑Нильсен, Джефф Хинтон, Джон Хопфилд, Янн ЛеКун, Джерри Леттвин, Джером Лурадур, Марвин Мински, Эрик Мьолснесс, Кайден Пирс, Томазо Поджио, Маттео Сальварецца, Терри Сейновски, Оливер Селфридж, Гордон Шоу, Йонас Сьёберг, Илья Суцкевер, Герри Тесауро и Тимоти Вердье. За помощь в работе над этой статьей я хотел бы особо поблагодарить Джулио Алессандрини и Брэда Кли.