Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
Благодаря технологии блокчейн, криптовалютам, криптобиржам, приоритеты людей, компаний и даже стран меняются прямо на наших глазах. Один знакомый разработчик из этой сферы однажды сказал мне, что не возлагает больших надежд на все это, несмотря на перспективы и хорошую оплату. Однако присутствует некое чувство неуверенности. "Водопровод, — говорит он, — казалось бы, одна из самых простейших технологий, но как она изменила жизнь. Когда в конце 90-х в моей небольшой деревне в моем доме появилась вода, которую не нужно было добывать большим трудом, жизнь действительно стала на порядок лучше и приятнее." Блокчейн, по его словам, сейчас является чем-то вроде того же водопровода - он обязательно изменит жизнь к лучшему, но сколько труда и времени для этого понадобится?
Чувство неуверенности касаемо блокчейна, криптобирж и криптовалют характерно не только для тех, кто занимается развитием и внедрением блокчейна, но и для его конечных пользователей, что и неудивительно, если брать во внимание количество провальных и мошеннических проектов. При этом не стоит забывать, что есть целая куча потрясающих исключений: недавно мы сами активно прорабатывали возможность создания блокчейн-биржи для ваучеров гражданской авиации. Проект перспективный и может иметь полезное применение, но, к сожалению, пока был отложен.
Полученный опыт все равно необходимо куда-то прикладывать, поэтому мы взялись за другую, очень схожую технологию, а именно торговлю криптовалютами на P2P-платформах и спотовых рынках. Как и в задуманной нами ранее бирже, такие площадки позволяют пользователям напрямую и без посредников покупать и продавать свои цифровые активы, а некоторые, наиболее предприимчивые пользователи могут даже зарабатывать на арбитраже. В данной статье мы рассмотрим математическую "начинку" арбитража и заодно выясним, как можно повысить эффективность заработка на нем.
Введение
P2P-платформа - это, как правило, внутрибиржевый обменник. Криптобиржа создает площадку, где пользователи могут создавать ликвидность, т.е. размещать ордеры на покупку или продажу, а другие пользователи могут эту ликвидность потреблять, т.е. совершать покупку или продажу активов по указанным в ордерах ценам. Биржа в данном случае выступает в качестве гаранта некоторого уровня безопасности таких сделок, взымая небольшую комиссию за определенные действия. Из-за того что P2P-платформа является частью самой биржи, причем внутри платформы находится множество валютных площадок (торговать можно как за рубли, так и доллары, евро и даже танзанийские шиллинги), а также из-за вероятностной природы спроса и предложения всегда возникают некоторые различия цен на один и тот же актив на разных площадках. Именно эти различия и являются основой для арбитража.
С тем, что такое P2P-арбитраж, можно ознакомиться в статьях компании @MediaMetriqa. Техническая сторона вопроса больше относится к разработке, на чем мы не будем заострять внимание. Хотя, стоит отметить, что сложность этого вопроса сильно увеличивается по мере роста требований к системе, выполняющей поиск - так называемых "связок". Связка - это возможность купить актив подешевле и продать его подороже с описанием, где и как это можно сделать, то есть некая совокупность доступных в текущий момент времени возможностей, способов оплаты, площадок, валют для получения прибыли с P2P-торговли.
Изначально мы поставили задачу по созданию сервиса, предоставляющего такие связки, однако практически сразу же столкнулись с трудностями. Сложность заключалась не в том, чтобы "прокручивать" на P2P-платформах небольшие суммы по простым связкам, а в том, что весь процесс упирается в потолок объема торгов и ограниченную скорость выполнения действий. Очевидный выход - разбить всю сумму на части и прокручивать их по разным связкам. Но тогда возникает другой вопрос: как это сделать, да и есть ли способ наиболее эффективного управления таким процессом? Данный вопрос является отправной точкой нашего исследования.
Единственный источник информации о торгах на P2P-платформах - это книги ордеров. Книги используются для поиска связок, но для более эффективного управления процессом арбитража одних лишь связок недостаточно. Например, нет никакой гарантии, что связка просуществует достаточное количество времени или будет исполнена быстро, что зачастую приводит к упущенным возможностям для арбитража по другим появляющимся связкам. Даже когда связок нет, нужно иметь возможность оценивать вероятность их появления, чтобы перераспределить средства на случай их появления. Это означает, что нужны какие-то метрики, позволяющие более-менее легко анализировать динамику всей книги ордеров.
Динамику книги ордеров определяют три типа действий:
размещение в книге лимитного ордера - обозначение возможности купить/продать заданный объем актива по заданной цене;
купля/продажа всего объема актива доступного по ордеру или же его части, причем купля/продажа может выполняться по ордеру с не самой лучшей ценой;
отмена ордера, т.е. его удаление из книги ордеров.
Сразу стоит отметить, что информация об отмене ордеров недоступна на P2P-платформах и отмена выглядит, как рыночное исполнение. Если некоторый участник решил отменить свой ордер, значит он руководствовался некоторым перечнем причин, которым мог бы руководствоваться покупатель/продавец актива по его ордеру. Пока нет необходимости в абсолютно точном моделировании динамики книги ордеров, поэтом достаточно некоторой метрики, пригодной для ее понимания.
Динамику книги заявок проще всего представить на дискретной сетке цен в виде следующего процесса:
где - обозначает валютную пару книги ордеров, а
обозначает суммарный объем ордеров на покупку/продажу по цене
.
За основу метрики возьмем принцип, лежащий в основе хорошо известного процесса дисбаланса. Теория дисбаланса создана на основе биржевой торговли, в то время как торговля на P2P-платформах имеет значительные отличия. Чтобы проиллюстрировать эти отличия, а также основные моменты P2P-торговли, создадим две вспомогательные функции:
Python
# необходимые импорты
import numpy as np
import networkx as nx
from scipy.stats import beta, poisson, norm, gamma
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import matplotlib.patches as mpatches
%config InlineBackend.figure_format = 'svg'
Функцию для моделирования книги ордеров:
Python
def create_book(d_m_min, d_m_max, s_m_min, s_m_max, punct):
dem_prices = np.arange(d_m_min, d_m_max + .1, punct)
num_dem_orders = poisson.rvs(10*beta.pdf(dem_prices, 3, 6, d_m_min, d_m_max-d_m_min))
dem_orders = [[int(gamma.rvs(5, 0, 500)) for i in np.r_[:num]] for num in num_dem_orders]
sup_prices = np.arange(s_m_min, s_m_max + .1, punct)
num_sup_orders = poisson.rvs(10*beta.pdf(sup_prices, 3, 6, s_m_min, s_m_max-s_m_min))[::-1]
sup_orders = [[int(gamma.rvs(5, 0, 500)) for i in np.r_[:num]] for num in num_sup_orders]
book = {'dem': {'prices': dem_prices, 'orders': dem_orders},
'sup': {'prices': sup_prices, 'orders': sup_orders},
'punct': punct}
return book
В данной функции для моделирования использовано бета-распределение, что не совсем согласуется с теорией. Посредством наблюдений зачастую выясняется, что такие распределения имеют положительный эксцесс (острота пика выше нормального значения), асимметрию и тяжелый хвост (в котором нельзя пренебрегать крупными, но редкими событиями). Ниже приведена KDE (ядерное сглаживание - один из способов оценки плотности распределения) распределения ордеров на покупку/продажу USDT:
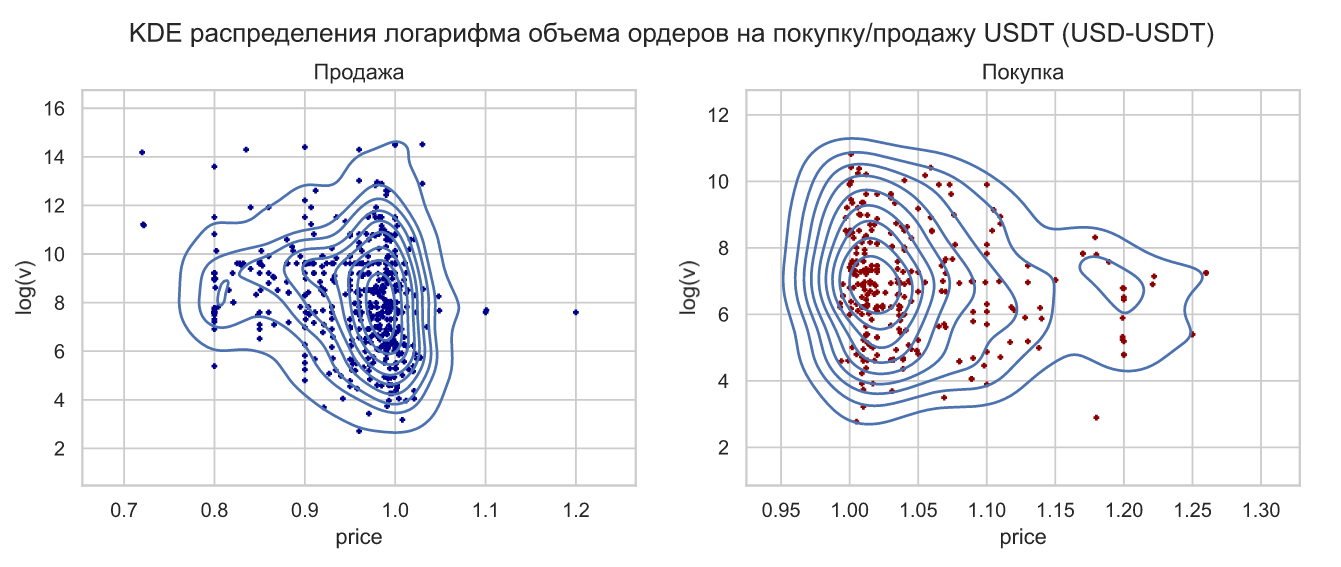
Считается, что количество ордеров является случайным процессом с двумя источниками энтропии, один из которых влияет на другой. Первый источник является внутренним и объясняется большим количеством различных стратегий поведения участников торгов, а второй - внешний и объясняется потоком информации, поступающей извне и влияющей на поведение участников. Именно поэтому в функции выше используются два распределения: бета-распределение определяет параметры пуассоновского распределения, а оно уже моделирует количество ордеров по разным ценам. Объем ордеров моделируется гамма-распределением. В результате работы данной функции получаем следующую структуру, имитирующую книгу ордеров:
Python
np.random.seed(42)
book = create_book(d_m_min=58, d_m_max=63,
s_m_min=65, s_m_max=70,
punct=.5)
book
Результат
{'dem': {'prices': array([58. , 58.5, 59. , 59.5, 60. , 60.5, 61. , 61.5, 62. , 62.5, 63. ]),
'orders': [[],
[4301, 2097, 1793, 2455],
[1742],
[2032, 2318, 1367, 3339, 1247],
[1172, 2552],
[3225, 2523],
[2210],
[],
[],
[],
[]]},
'sup': {'prices': array([65. , 65.5, 66. , 66.5, 67. , 67.5, 68. , 68.5, 69. , 69.5, 70. ]),
'orders': [[],
[],
[],
[],
[2022],
[2256, 3593],
[2745, 4420, 493, 3338, 2428],
[2025, 2104, 2740],
[1564, 1832, 3468, 2706],
[2439, 3543],
[]]},
'punct': 0.5}
Создадим еще одну функцию для визуализации получаемых моделей:
Python
def plot_book(book, ax):
width = book['punct'] - .2*book['punct']
dem_order_levels = [np.cumsum(i)[::-1] for i in book['dem']['orders']]
for i in np.r_[:len(book['dem']['prices'])]:
for j in np.r_[:len(dem_order_levels[i])]:
if j == 0:
ax.bar(book['dem']['prices'][i], dem_order_levels[i][j],
edgecolor='0.2', fill=False,
width=width, zorder=10)
ax.bar(book['dem']['prices'][i], dem_order_levels[i][j],
color='r', alpha=0.3, label='Demand',
width=width, zorder=10)
ax.bar(book['dem']['prices'][i], dem_order_levels[i][j],
edgecolor='0.2', fill=False,
width=width, zorder=10)
sup_order_levels = [np.cumsum(i)[::-1] for i in book['sup']['orders']]
for i in np.r_[:len(book['sup']['prices'])]:
for j in np.r_[:len(sup_order_levels[i])]:
if j == 0:
ax.bar(book['sup']['prices'][i], sup_order_levels[i][j],
edgecolor='0.2', fill=False,
width=width, zorder=10)
ax.bar(book['sup']['prices'][i], sup_order_levels[i][j],
color='b', alpha=0.3, label='Supply',
width=width, zorder=10)
ax.bar(book['sup']['prices'][i], sup_order_levels[i][j],
edgecolor='0.2', fill=False,
width=width, zorder=10)
dem_label = mpatches.Patch(facecolor='r', alpha=0.3, label='Demand')
sup_label = mpatches.Patch(facecolor='b', alpha=0.3, label='Supply')
ax.legend(handles=[dem_label, sup_label], loc='upper center')
ax.grid(axis='y',color='0.93')
ax.set_xlabel('Price')
ax.set_ylabel('Volume')
Python
fig, ax = plt.subplots(figsize=(10, 5))
plot_book(book, ax)
ax.axvline(x = (61+67)/2, ls='--');

Высота каждого столбца - это суммарный объем актива ордеров по соответствующей цене, а высота каждого прямоугольника в столбце - объем актива отдельного ордера. На этом графике изображена ситуация, в которой арбитраж невозможен - купить актив дешевле и затем продать его дороже не получится. Пунктирной линией обозначена рыночная средняя цена (mid price). Обычно на биржах все пытаются спрогнозировать именно среднюю цену, в то время как на P2P-платформах в этом нет особого смысла, поскольку реальная стоимость покупки/продажи определяется именно ценами ордеров.
Очередное отличие от автоматической торговли на бирже заключается в том, что на P2P-платформах покупатель или продавец актива может выбирать среди ордеров с одинаковой ценой тот, который максимально точно соответствует его предпочтениям, без всякой очередности. Выбор может опираться на такие критерии, как: рейтинг участника, разместившего ордер, объем ордера или способ оплаты.
Рассмотрим книгу ордеров, содержащую возможность для арбитража:
Python
np.random.seed(0)
book = create_book(d_m_min=59, d_m_max=68, s_m_min=60, s_m_max=70, punct=.5)
fig, ax = plt.subplots(figsize=(10, 5))
plot_book(book, ax)
ax.axvline(x=62, c='k', ls='--', zorder=11)
ax.axvline(x=67, c='k', ls='--', zorder=11);

На данном графике видно, что ценовые диапазоны ордеров предложения и спроса пересекается, образуя тем самым интервал (обозначен пунктирной линией), в котором возможен арбитраж. Данный график также показывает двоякое отношение к связкам, которые могут восприниматься как в буквальном, так и вероятностном контексте. В буквальном контексте связка означает четкие указания к действию, например: покупаем USDT за доллары по ордеру "А", потом продаем за евро по ордеру "В". В вероятностном контексте связка означает, что на данный момент ордеров на покупку и продажу может и не быть, но вероятность их долгого отсутствия очень мала. Именно это и означает возможность, а не гарантию: ордеры могут появляться и исчезать быстрее скорости перемещения указателя мыши.
Арбитражная область на графике, отмеченная пунктирной линией, несколько шире области, в которой происходит перекрытие столбцов. Это связано с вероятностной природой появления и исчезновения ордеров. Арбитражную область можно рассматривать как границы соответствующих распределений плотности вероятностей количества ордеров на покупку и продажу в определенный момент времени.
Изображенная на графике ситуация выглядит так, словно есть возможность "заарбитражить" один и тот же актив на единственной площадке, что может показаться невозможным. Однако встречаются ситуации, когда это возможно: например, долгое время на P2P-платформе Binance в паре RUB-USDT наблюдалась именно такая ситуация, когда, купив USDT за рубли через банк Тинькофф, их можно было продать дороже через Сбер.
С другой стороны, даже более сложную связку, например, такую
все равно можно разместить на одном графике. В конце концов, чтобы узнать прибыль по связке, нам придется добавить фиктивное действие в ее конец (или начало). В итоге исходную связку можно записать как:
воспринимая как простой актив.
Представим ситуацию с прокручиванием довольно значительных сумм по множеству связок. И интересует нас понимание, где (по каким валютным цепочкам) эти случайные связки вообще возможны, а где нет. Для этого нужны метрики, позволяющие оценивать наличие возможностей для арбитража, интенсивности их появления и привлекательности. На данный момент у участников торгов на P2P-платформах до сих пор нет никаких специализированных индикаторов и инструментов для проведения технического анализа.
Индикаторы арбитражных ситуаций на p2p
Казалось бы, в арбитраже нет ничего сложного: покупаем подешевле, продаем подороже - готово! Раз в основе лежит такая простая схема, значит и в основе метрик, позволяющих отслеживать арбитражные ситуации, все тоже должно быть предельно просто. Например, чтобы обнаружить возможность для арбитража, может оказаться достаточным наблюдать за KDE книги ордеров:
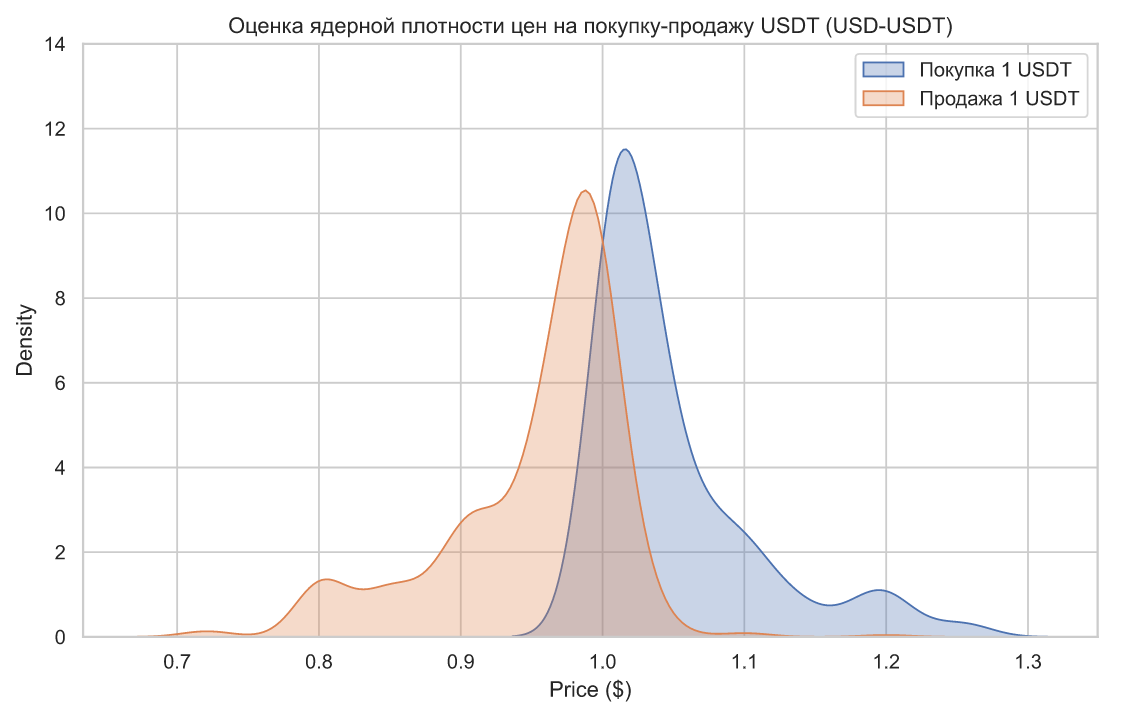
На этом графике видна существующая возможность для арбитража. Как давно появилась эта возможность? Каков ее потенциал в контексте объема актива и какова интенсивность торгов? На все эти вопросы ответить не получится. Можно попробовать визуализировать отсортированную часть наиболее выгодных предложений, изобразив их в виде линий:
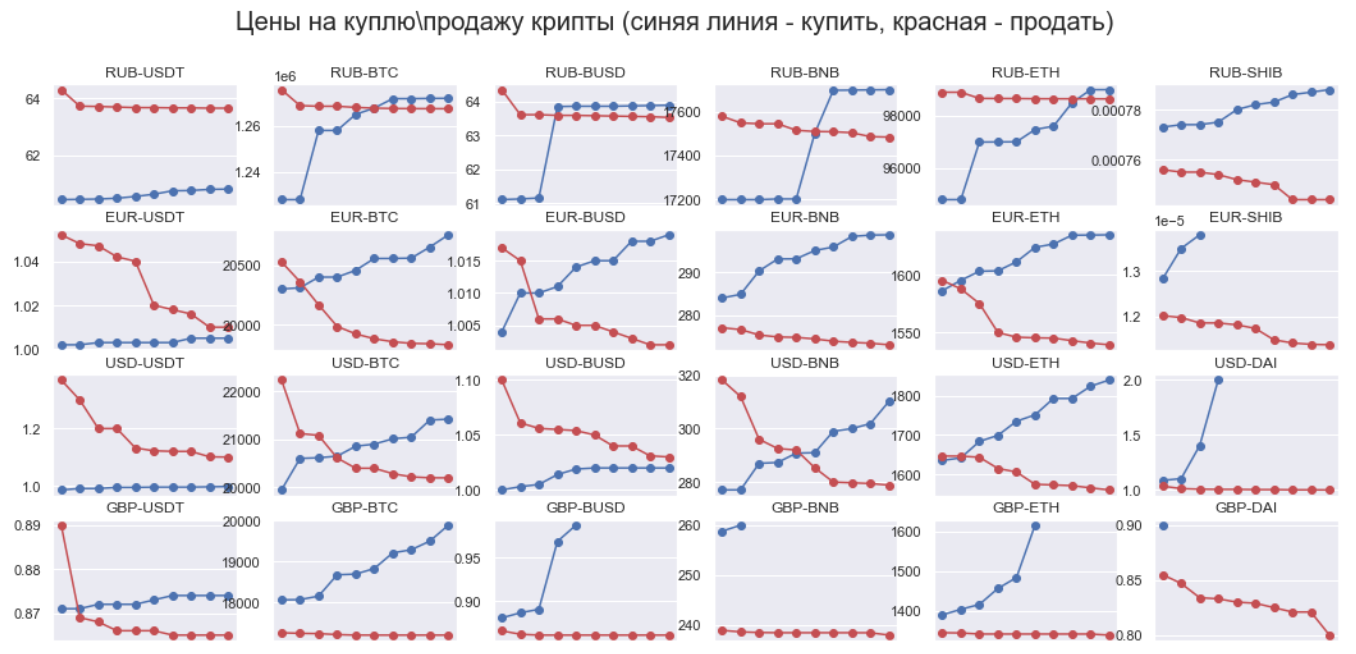
Несмотря на крайне простую идею, которая лежит в основе арбитража, придумать простую метрику не выходит. Можно выдвинуть несколько очевидных задач, которые можно постараться решить с помощью метрик:
отслеживание динамики книги ордеров;
отслеживание ширины арбитражного интервала;
отслеживание объема средств в арбитражном интервале, которое необходимо потому, что арбитражный интервал может быть очень широким, но таким, что большая часть ордеров в нем может оказаться с небольшим объемом актива;
отслеживание интенсивности торгов, которое необходимо, потому что даже несмотря на большую ширину арбитражного интервала и объем средств в нем, низкая или высокая интенсивность торгов может оказаться важным параметром для понимания ситуации.
Данные для прототипа метрик возьмем с криптобиржи Binance. Следующий код позволяет делать снимки необходимой книги ордеров:
Python
import requests
data = {
"asset": "ETH",
"fiat": "GBP",
"merchantCheck": False,
"page": 1,
"payTypes": [],
"publisherType": None,
"rows": 20,
"tradeType": "BUY" # BUY / SELL
}
headers = {
"Accept": "/",
"Accept-Encoding": "gzip, deflate, br",
"Accept-Language": "ru-RU,ru;q=0.8,en-US;q=0.5,en;q=0.3",
"Cache-Control": "no-cache",
"Connection": "keep-alive",
"Content-Length": "123",
"content-type": "application/json",
"Host": "p2p.binance.com",
"Origin": "https://p2p.binance.com",
"Pragma": "no-cache",
"TE": "Trailers",
"User-Agent": "Mozilla/5.0 (Windows NT 10.0; Win64; x64; rv:88.0) Gecko/20100101 Firefox/88.0"
}
r = requests.post('https://p2p.binance.com/bapi/c2c/v2/friendly/c2c/adv/search', headers=headers, json=data)
Binance позволяет делать снимки не более чем из 20-ти самых выгодных по цене ордеров, а не всей книги. Сбор данных выполнялся в начале октября 2020 года, снимки делались каждые 15 минут на протяжении суток. Частота совершения снимков не позволяет исследовать интенсивность торгов, но вполне пригодна для демонстрации принципа построения метрик, а в качестве основы возьмем связку .
Mid price
Mid price - это, пожалуй, самая неинформативная метрика. Она не несет полезной информации об арбитражных ситуациях. Тем не менее, это производная величина от цен bid и ask, так что она заслуживает хотя бы формального присутствия на дашборде.
Применительно к связке mid price будет выглядеть следующим образом:
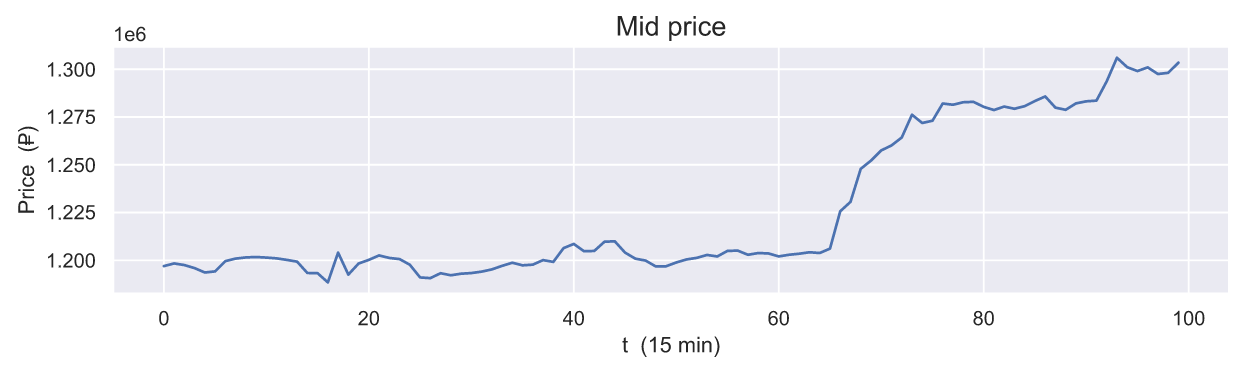
Для оценки арбитражной ситуации важнее наблюдать непосредственно за самими ценами bid и ask: если ask меньше bid, то мы получаем ситуацию, в которой возможен арбитраж.
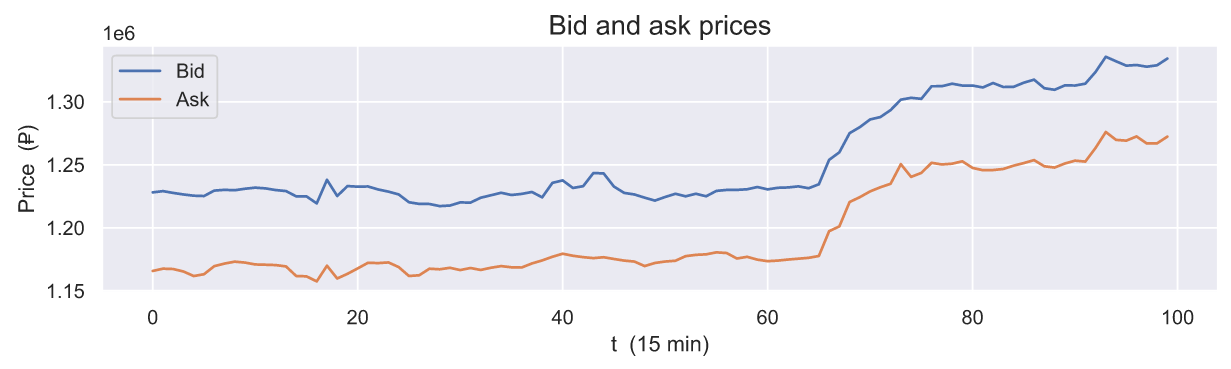
На данном графике видно, что на протяжении всего рассматриваемого времени есть возможность для прокручивания средств по данной связке. Однако наличие арбитражной ситуации не означает, что прокрутка легко осуществима.
Spread
Спред (распределение, spread) позволяет следить за шириной арбитражного интервала.
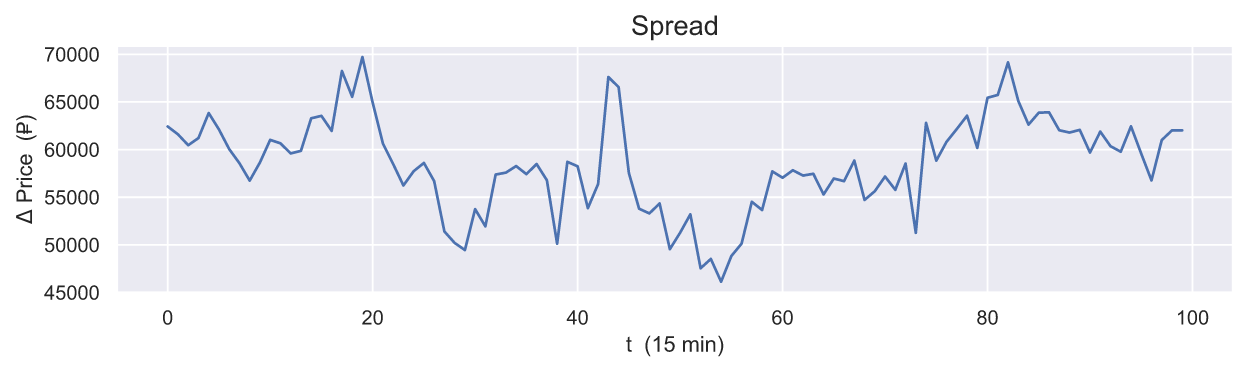
Объем актива в арбитражном интервале
Очевидно, чем шире арбитражный интервал и чем больше объем средств в нем располагается, тем лучше. Однако объем рассматривается как меньший суммарный объем ордеров сторон спроса и предложения, располагающихся внутри интервала.
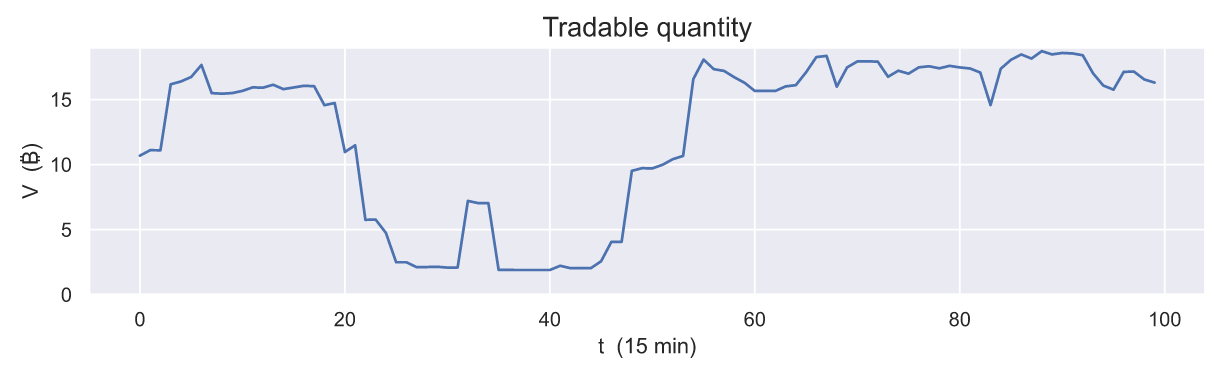
В данном случае весь объем целиком представлен китайским предложением, поскольку спрос на биткоин на российской площадке многократно больше:
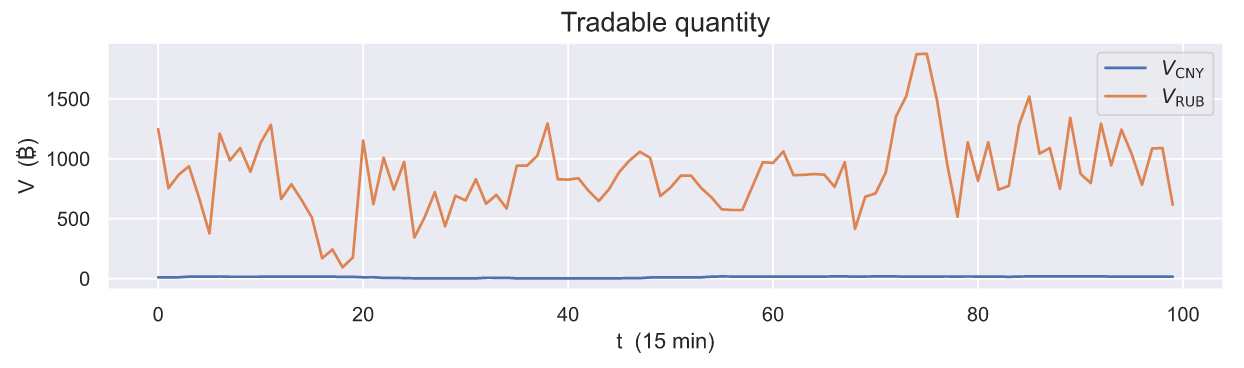
Средняя цена взвешенная по объему
Средняя цена, взвешенная по объему, является очень простой метрикой и может быть вычислена по следующим формулам:
где ,
- цена и объем
-го ордера стороны предложения, а
,
- цена и объем
-го ордера стороны спроса.
Несмотря на простоту, данная метрика уже может сообщать о дисбалансе, например, их среднее арифметическое в идеале должно совпадать со средней ценой. Данная метрика позволяет оценить цену, по которой продается или покупается наибольшая часть актива. Любое изменение данной метрики свидетельствует об изменении внутри книги ордеров и является стимулом для ее более тщательного анализа.
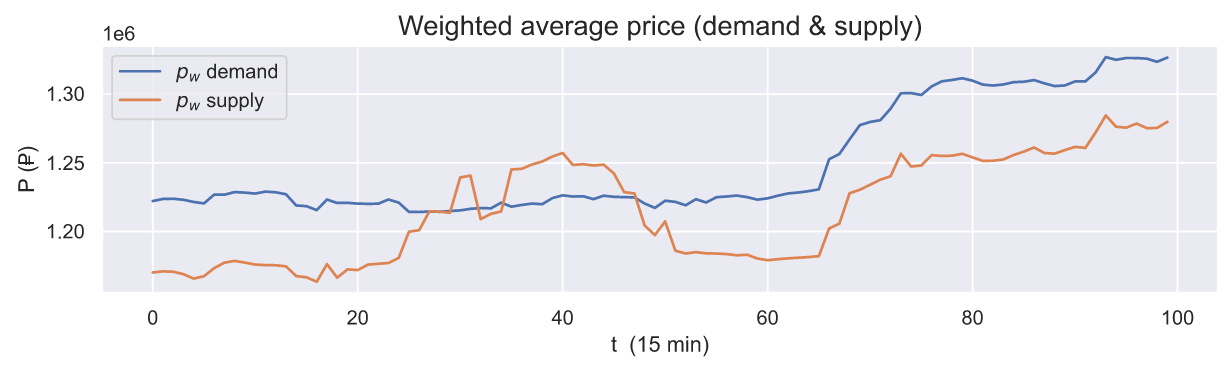
На вышеприведенном графике видно, что значительная часть ордеров предложения выросла в цене, хотя спред показывает наличие арбитражной ситуации. Это может свидетельствовать о том, что арбитражный интервал образуют лишь ордера с ценами bid и ask, причем как минимум один из них имеет крайне малый объем.
Тем не менее, для оценки арбитражной ситуации важно понимать не только по какой цене торгуется или продается большая часть актива, но видеть разницу между и
:
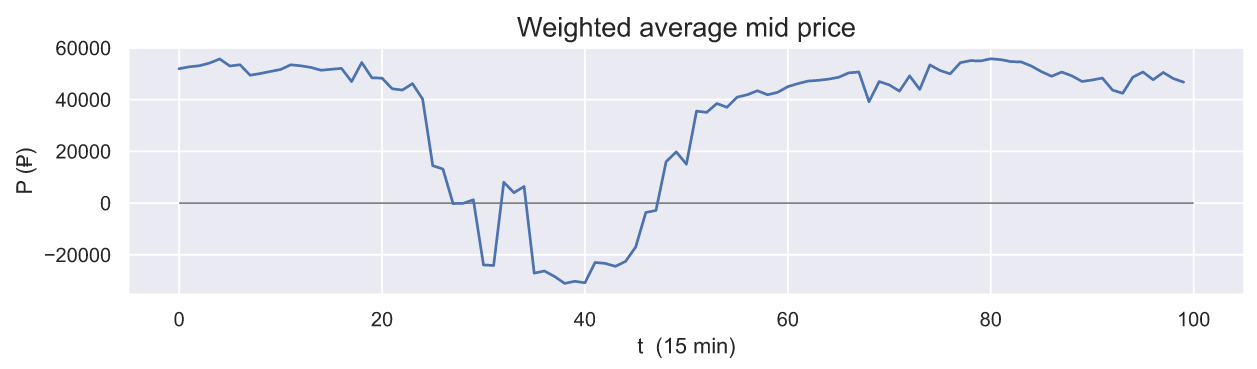
Приближение такой линии к 0 снизу говорит о том, что цены сторон спроса и предложения движутся навстречу друг другу. А в случае принятия положительных значений мы имеем сигнал о том, что значительная часть ордеров на покупку стоит дешевле, чем на продажу, что является явным признаком арбитражной ситуации.
Дисбаланс
В идеальной ситуации книга ордеров должна находиться в динамическом равновесии.
Если обозначить разницу цен ордеров из соответствующих друг другу позиций в книге как
то баланс по цене может быть вычислен как простая разность:
При мы имеем идеальный баланс, который может существовать только в теории. Причем само по себе значение
не позволяет однозначно делать какие-то выводы о динамике дисбаланса. Попробуем отобразить на графике соответствующие каждой стороне суммы по отдельности:
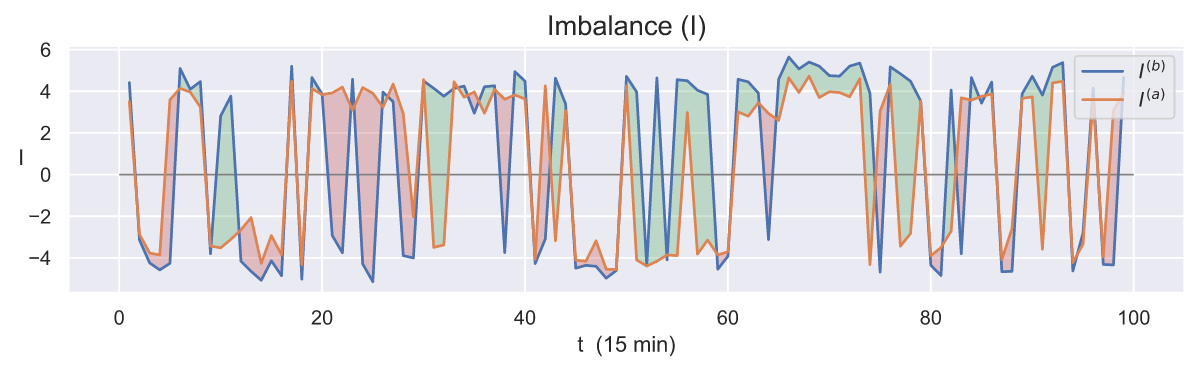
Данный график показывает, что когда линия выше 0, а линия
ниже 0, то это означает, что стороны спроса и предложения движутся навстречу друг другу или движутся в разные стороны, если
, а
. В случае если и
и
имеют одинаковый знак, то это означает, что они движутся в одну и туже сторону "+" - вправо, "-" - влево.
Если интересует только разнонаправленное движение, то можно заменить две линии и
на одну по следующему правилу:
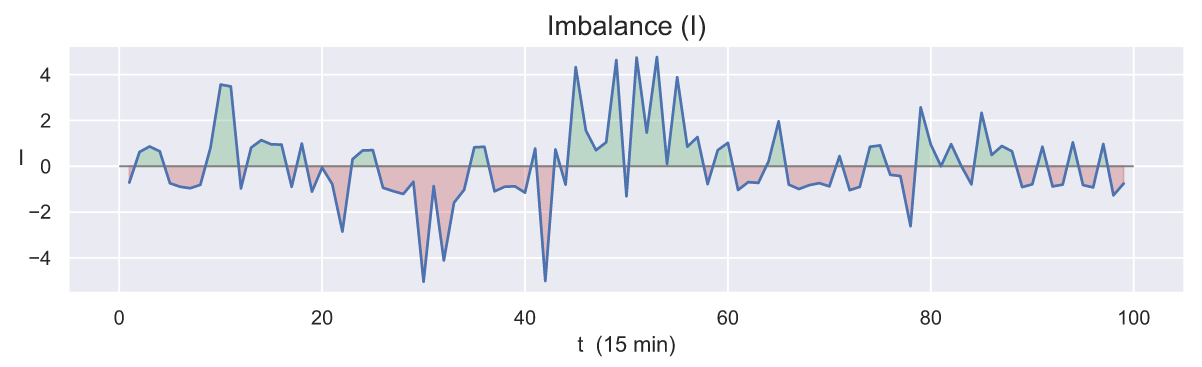
Зеленые области данного графика говорят о том, что ордера спроса и предложения движутся навстречу друг другу (арбитражный интервал может появиться или расшириться если он уже существует), а красные, наоборот, о том, что они движутся в разные стороны (арбитражный интервал может сузиться или вовсе исчезнуть).
Объединение метрик на едином дашборде
Чтобы понять, как наблюдение за всеми представленными метриками в совокупности, может помочь для анализа и оценок арбитражных ситуаций возьмем связку .
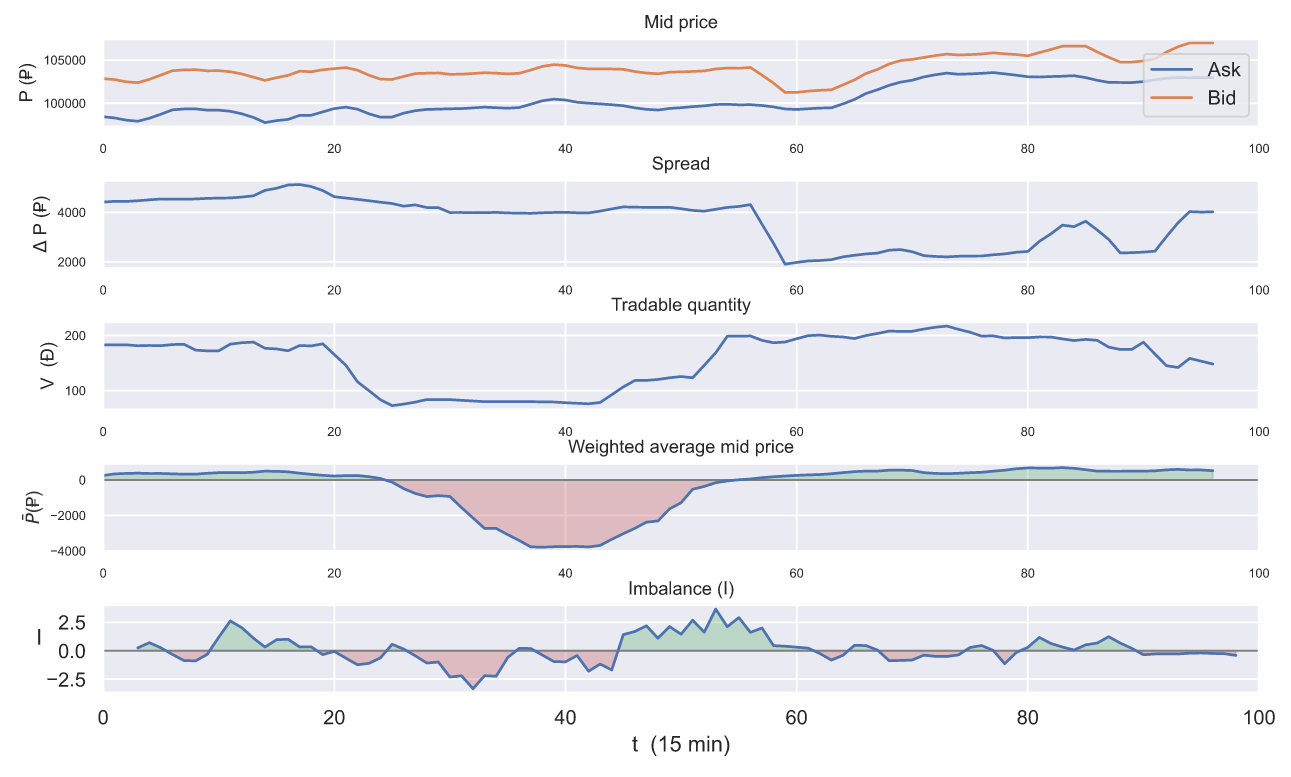
Первые два графика могут вызывать чрезмерный оптимизм, а три последних графика уже позволяют трезво оценивать ситуацию. Например, график объема при t=25 должен вызвать как минимум настороженность. При t=25 взвешенная по объему средняя цена также становится отрицательной, что сигнализирует о том, что количество ордеров, подходящих для арбитража, начинает уменьшаться. При t=20 ордеры спроса и предложения начинают двигаться в противоположные стороны. Это говорит о возрастающих рисках "застрять" в невыгодной позиции, что должно заставить прокручивать меньшие средства по данной связке либо вообще прекратить ее использование, пока ситуация не изменится.
Представленные индикаторы заставляют связки "говорить" на более простом и понятном языке, позволяя проводить более адекватную оценку состояния торгов и возможных рисков. Разумеется, это не означает, что работа с самой книгой ордеров больше не нужна, наоборот, данные индикаторы позволяют понять, когда и к каким именно книгам надо обращаться, чтобы более продуктивно тратить время на их непосредственный анализ.
Диверсификация
Очевидно, что доходность от связок является случайной величиной. Вполне естественной является ситуация, когда связки, начинающиеся с BTC, в определенный период времени приносят доход больший, чем связки, начинающиеся с ETH, а затем наоборот. В каждый из этих периодов времени для извлечения наибольшей выгоды на кошельках арбитражера должна поддерживаться наиболее выгодная пропорциональность этих криптовалют. Необходимо подобрать и придерживаться таких долей криптовалют, чтобы обеспечить максимальную доходность.
Задача формулируется следующим образом: есть криптовалют, доходности каждой криптовалюты являются случайными величинами с матожиданием
и отклонением
, при этом доходности двух криптовалют с индексами
и
связаны корреляцией
. Необходимо подобрать такие доли криптовалют
чтобы портфель с доходностью
имел наименьшую дисперсию:
где ,
и
это матрицы-столбцы, а
- матрица, задающая парные связи отклонений и корреляций криптовалют:
Арбитражер - это не инвестор, но арбитражер с большим количеством средств не должен забывать о том, что каждая криптомонета в его кошельках является инвестицией. Помимо доходности от арбитража, каждая криптовалюта имеет свою собственную доходность, определяемую рынком. Доходность по некоторым криптовалютам из-за большой дисперсии может запросто принимать отрицательные значения.
Портфельная теория очень удобна для понимания некоторых нюансов арбитража, но это не значит, что она может объяснить абсолютно все в этой деятельности. Мы также должны руководствоваться подверженностью к риску. Чтобы продемонстрировать практическую разницу между минимальным и приемлемым риском, рассмотрим простой пример. Пусть связки, начинающиеся с BTC, показывают доходность в 2.5% с отклонением 0.5%, а связки, начинающиеся с ETH, имеют доходность в 3.7% с отклонением 1.1%. Выясним, при каком соотношении криптовалют отклонение будет наименьшим.
Математическое ожидание вычисляется по следующей простой формуле:
где и
- доли BTC и ETH,
и
- доходности BTC и ETH.
Чуть сложнее вычисляется дисперсия:
где - коэффициент корреляции между
и
, а
и
их стандартные отклонения. Предположим, что коэффициент корреляции имеет небольшое отрицательное значение равное -0.1. Тогда зависимости отклонения и доходности портфеля от доли BTC будут выглядеть следующим образом:
Python
f, ax = plt.subplots(1, 2, figsize=(12, 4))
w = np.linspace(0, 1)
v = (0.52 * w2 + 1.1**2 * (1 - w)**2 + 2w(1 - w)(-0.1)0.51.1)**0.5
e = w2.5 + (1-w)*3.7
ax[1].plot(w, e)
ax[1].axvline(w[np.argmin(v)], color='0.3', ls=':')
ax[1].axhline(e[np.argmin(v)], color='0.3', ls=':')
ax[1].set_xlabel('Доля BTC')
ax[1].set_ylabel('Доходность (%)')
ax[1].set_title('Зависимость доходности от доли BTC')
ax[0].plot(w, v)
ax[0].axvline(w[np.argmin(v)], color='0.3', ls=':')
ax[0].axhline(min(v), color='0.3', ls=':')
ax[0].set_xlabel('Доля BTC')
ax[0].set_ylabel('Отклонение')
ax[0].set_ylim(0.35, 1.15)
ax[0].set_title('Зависимость отклонения от доли BTC');
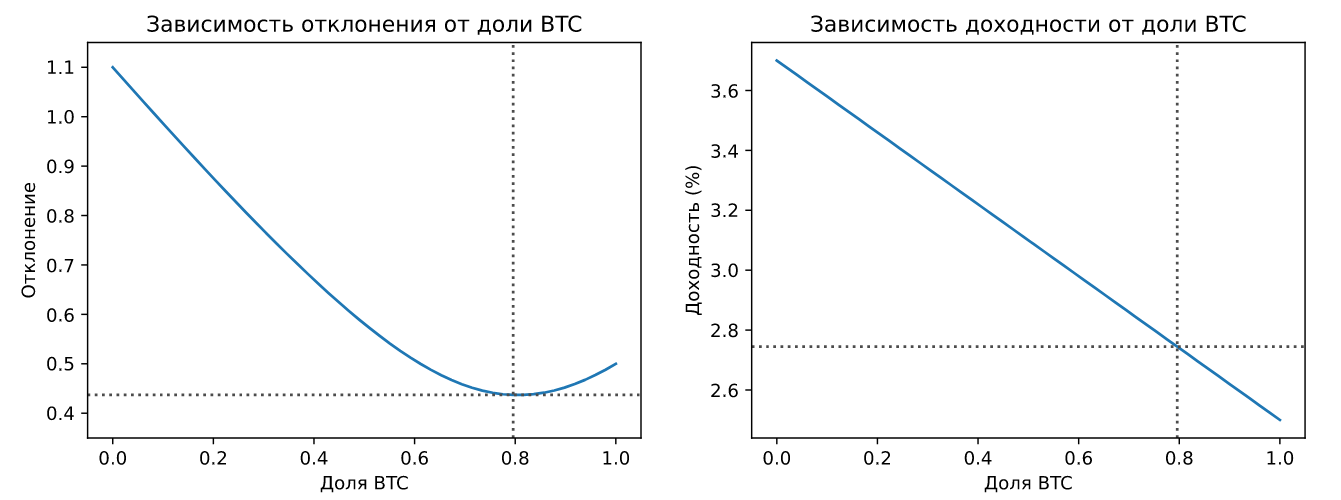
Портфель, состоящий на 80% из BTC и 20% ETH, позволяет на 10% снизить отклонение и на 10% увеличить доходность по сравнению с портфелем, состоящим на 100% из BTC. Сравним распределение доходностей найденного "оптимального" портфеля и распределение доходностей у портфеля, состоящего на все 100% из ETH:
Python
x = np.linspace(0, 8, 300)
y1 = norm.pdf(x, e[np.argmin(v)], min(v))
y2 = norm.pdf(x, 3.7, 1.1)
plt.plot(x, y1, label='20% ETH, 80% BTC')
plt.plot(x, y2, label='100% ETH')
ppf_01 = norm.ppf(0.01, e[np.argmin(v)], min(v))
plt.axvline(ppf_01, c='k', lw=1)
plt.axhline(0, c='k', lw=1)
x = np.linspace(0, ppf_01)
y = norm.pdf(x, 3.7, 1.1)
plt.fill_between(x, y, alpha=0.9, color='orange')
plt.legend()
plt.title('pdf доходностей двух портфелей');
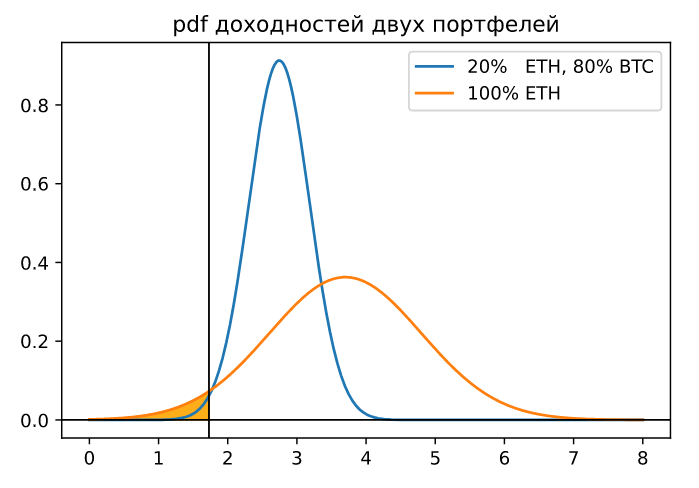
Портфель, состоящий только из ETH, в 20% случаев будет давать доходность меньшую, чем у портфеля с минимальным отклонением, а в оставшихся случаях его доходность будет большей.
Как понять, приемлем ли риск этого портфеля? Найдем квантиль доходности оптимизированного портфеля с уровнем 0.01 и затем вычислим, с какой вероятностью доходность портфеля, состоящего только из ETH, окажется меньше даного квантиля. Если данная вероятность окажется меньше заранее оговоренного значения, например 0.05, то риск считается приемлемым. В нашем случае эта вероятность составляет всего 0.036 (на графике закрашена оранжевым цветом).
Приемлемый или допустимый риск можно определить как риск, при котором вероятность сожалеть об упущенной выгоде очень мала.
Функция полезности
Связка - это цепочка обменов, в которой одни обмены могут выполняться на P2P-платформах, а другие на спотовых рынках. Глядя на связку, особенно длинную, в первую очередь хотелось бы понять, как сильно переоценены или недооценены активы в каждом ее обмене. Мы знаем, что на обычном валютном рынке кросс-курсы валют могут быть в дисбалансе с обычными курсами. Допустим, у нас есть такие курсы:
BTC/USDT - 20361
ETH/USDT - 1554
ETH/BTC - 0.076380
На эффективном рынке частное цен (ETH/USDT) / (BTC/USDT) должно быть равно цене ETH/BTC. В вышеприведенных курсах разница всего 0.08%.
Если кросс-курсы недооценены, например, вместо 0.076380 будет 0.076080, то мы можем составить следующие цепочки обменов:
Посчитать доходность можно по простой формуле:
где - количество актива до прокрутки по цепочке,
- количество актива после прокрутки. Если предположить, что прокрутка выполняется для единичного актива, то для наших цепочек получим следующие одинаковые результаты:
Если кросс-курсы переоценены, вместо 0.076380 будет 0.076680, то получается вот такая цепочка:
с доходностью:
Обмены необязательно выполнять последовательно. Например, если обмены в цепочке выполняются на разных биржах, то, выполняя обмены параллельно, можно "протолкнуть" всю цепочку целиком и получить прибыль. Предположим, что каждому обмену в цепочке соответствует некоторая биржа и на каждой из них у нас имеется:
10 BTC;
300000 USDT;
100 ETH.
Мы хотим "протолкнуть" по последней рассмотренной цепочке 5 BTC, параллельно выполняя следующие действия:
Биржа №1: 5 BTC * 20361 = 101805 USDT;
Биржа №2: 101805 USDT / 1554 = 65.5115 ETH;
Биржа №3: 65.5115 ETH * 0.076680 = 5.0234 BTC.
Все это приведет к следующим изменениям располагаемых активов:
BTC: 10 - 5 + 5.023 = 10.023;
USDT: 300000 + 101805 - 101805 = 300000;
ETH: 100 + 65.511 - 65.511 = 100.
Это хорошо демонстрирует, как важно иметь разное количество разной криптовалюты на разных биржах, в определении оптимальных пропорций которой как раз и должна помочь портфельная оптимизация. Скорость реализации цепочек при это может быть значительно увеличена. Скорость - это преимущество в арбитраже.
Можем ли мы узнать, какой вклад вносит каждый внутренний обмен цепочки в ее итоговую доходность?
Для дальнейших рассуждений давайте предположим, что к рассмотренным выше валютным парам:
BTC/USDT - 20361;
ETH/USDT - 1554;
ETH/BTC - 0.076380.
Добавились следующие валютные пары:
BTC/TRY - 382524;
ETH/TRY - 29137;
USDT/TRY - 18.806.
Тогда мы можем составить еще более длинную цепочку обменов:
Исходя из курсов эффективного рынка (представленных выше) имеем следующую доходность:
Чтобы доходность цепочки увеличилась, достаточно чтобы BTC/TRY был переоценен, например, вместо 382524 стало 382724. А ETH/TRY недооценен, вместо 29137 стало бы 29007:
BTC/TRY - 382724 (было 382524);
ETH/TRY - 29007 (было 29137).
В этом случае мы получим следующую доходность:
Если при всем при этом недооценен BTC/USDT (стало 20261 вместо 20361) и переоценен ETH/USDT (стало 1574 вместо 1554):
BTC/USDT - 20261 (было 20361);
ETH/USDT - 1574 (было 1554).
То доходность цепочки увеличивается еще сильнее:
Теперь самое интересное. Имея тот же самый дисбаланс цен, мы можем разбить нашу длинную цепочку:
на две следующие цепочки:
По первой цепочке доходность составит:
По второй цепочке доходность составит:
Вопрос о доходности и целесообразности отдельных обменов в цепочке теперь можно перевести в более практический контекст: что лучше - прокручивать средства по цепочке из 4-х обменов с 2.5% доходности или по цепочке из 3-х обменов с 1.59% доходности?
Предположим, что мы каждый раз прокручиваем какую-то фиксированную сумму средств, например, 1 у.е. (простой процент), тогда в первом случае мы получим доходность:
Во втором случае:
Однозначно выигрывает длинная цепочка, так как ее доходность на 5.7% больше, чем у короткой.
А что, если каждый раз мы будем прокручивать сумму, включающую в себя предыдущий доход (сложный процент)? Ведь мы заинтересованы в наискорейшем росте прибыли, значит чаще всего мы будем поступать именно так. При таком поведении доходность длинной цепочки составит:
По короткой цепочке доходность будет равна:
Получается, что использование длинной цепочки становится еще выгоднее, так как в этом случае ее доходность будет уже на 7.74% больше. Однако, если длинная цепочка станет еще на один обмен длинее при тех же 2.5% доходности, то ситуация изменится, потому что за один час мы сможем выполнить не 15, а 12 прокруток. Такая цепочка покажет доходность:
А это уже на 2.61% меньше, чем для короткой.
Отсюда следует, что функция полезности, благодаря которой мы отдаем предпочтения тем или инным цепочкам, может быть представлена в следующей форме:
где - доходность, выраженная в процентах, а
- длинна цепочки.
Пусть длинная цепочка увеличилась не только с 4-х до до 5-ти обменов, но и доходность ее также возросла с 2.5% до 3.5%. Тогда мы получим существенный прирост доходности с 34.489% до:
Согласно введенной функции полезности, мы должны предпочесть длинную, а не короткую цепочку. Взглянем еще раз на наши цепочки обменов:
Допустим, есть два арбитражера, которые обладают одной и той же информацией: первый решил воспользоваться длинной цепочкой, а второй - короткой. Если они действуют одновременно, выполняя все в ручном режиме, учитывая, что ордеры ограничены по объему, то первый рискует застрять в BTC. Пока первый из них выполнит обмены , второй уже успеет обменять
, чем и разорвет длинную цепочку.
Неудивительно, что цепочка может разорваться. Причиной разрыва может послужить другой арбитражер, ведь разные цепочки могут иметь одинаковые участки. Также она может разорваться просто потому, что любой ордер из ее состава может приглянуться обычному участнику биржи. Застрять в BTC, как в вышеприведенном примере, нестрашно, так как никакой позиции на долгое время не открывается: в этом случае можно просто выполнить обмен, необходимый для прокручивания по другой цепочке, если таковой обмен вообще потребуется. Однако разрыв цепочки означает, что время, которое могло быть потрачено с пользой, будет упущено.
Отсюда следует, что функция полезности должна обладать вероятностью разрыва цепочки за время, необходимое для ее реализации. Чем меньше эта вероятность, тем лучше, если ее обозначить буквой , то функцию полезности можно записать как:
Оценить величину можно с помощью оценок временем жизни ордеров, входящих в цепочку. Оценить это время довольно непросто: во-первых, мы не можем фиксировать каждое изменение во всех книгах ордеров, ведь их сотни. Во-вторых, снимки книг не являются полными, то есть содержат какое-то фиксированное количество ордеров, как со стороны спроса, так и со стороны предложения.
Нас интересует лишь небольшая часть книги, содержащая диапазон цен, отличающихся от цен bid и ask не более чем на 0.5-1.5%. Данная область так же разбивается на более узкие, непересекающиеся диапазоны. Далее мы можем отслеживать долю ордеров из необходимого поддиапазона снимка, время жизни которых оказалось меньше . Продемонстрировать данный принцип можно на посекундных снимках книги ордеров пары BTC/USDT (август 2020 года). Для простоты возьмем со стороны спроса и предложения только один диапазон цен, отличающихся от цен bid и ask не более чем на 0.5%.

На графике видно, что изменение этой доли имеет некоторую зависимость от изменения цены, а данные по динамике цены получить гораздо проще, чем по динамике книги ордеров. В действительности, снимки ордеров выполняются намного реже, но если несколько раз в сутки делать снимки с максимально возможной частотой на протяжении 1.5-2.5 минут, то благодаря данным по изменению цены и простым моделям на основе случайных деревьев можно в любое время довольно точно оценить вероятность того, что некий ордер "проживет" меньше . Далее можно довольно просто оценить функцию выживаемости:
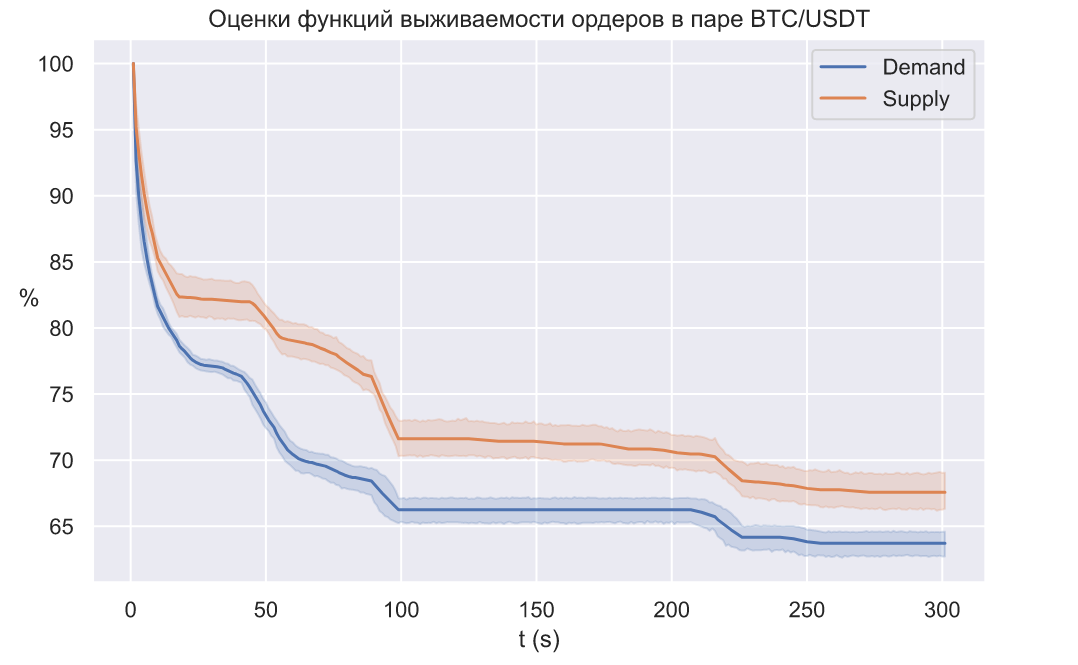
На основе оценок функций выживаемости ордеров по каждой валютной паре в цепочке и производится оценка .
Алгоритм поиска связок
Как искать связки в этом множестве различных бирж, криптовалют и тысяч валютных пар?
Взглянем на связку с доходностью около 3%:
В нашем случае необязательно должна быть одна и та же валюта, ведь для нас важен именно рост объема всех располагаемых средств. Мы можем запросто находить и использовать вот такие связки:
Все курсы валют относительны, и, чтобы понять, что объем средств действительно увеличился, нам придется вводить фиктивные обмены по актуальным курсам:
Получается, что все связки являются циклами, а не цепочками. Осталось только придумать, как находить эти циклы. Разумеется, циклы нужны с положительной и наибольшей доходностью.
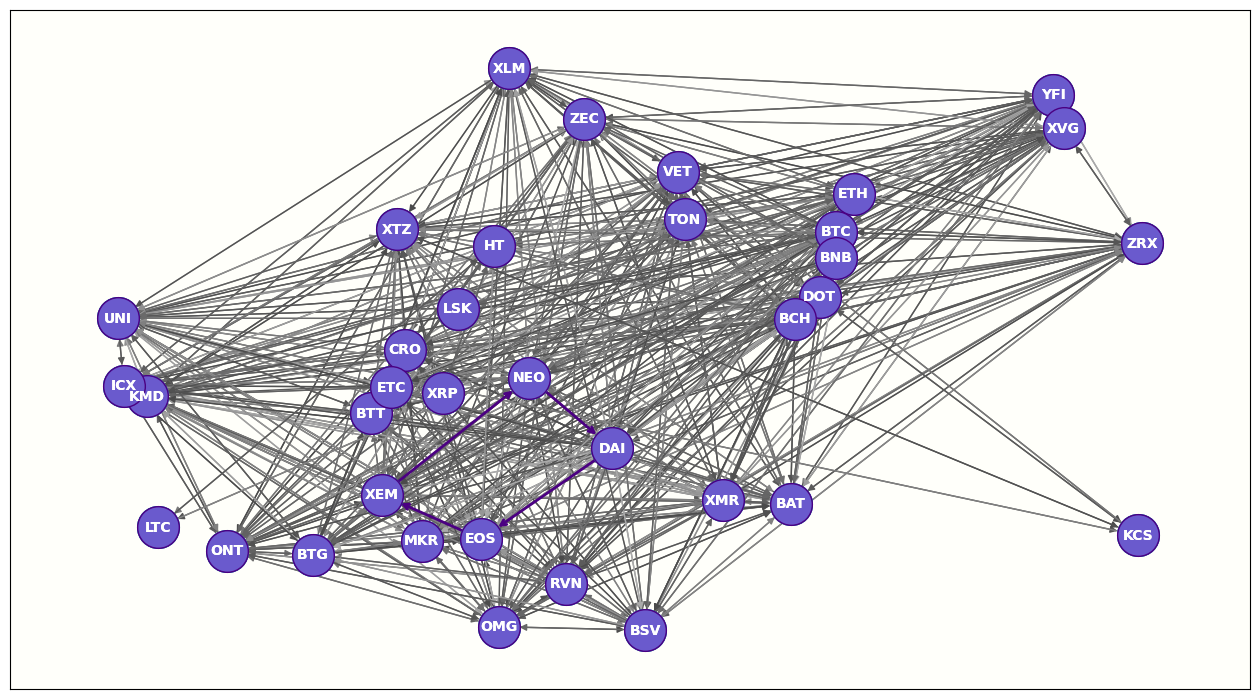
Создадим граф из десяти криптовалют, которые будут вершинами, а дугами будут ордера, обеспечивающие возможность сделки по обмену одной криптовалюты на другую. Возьмем цены bid и ask с 8-ми бирж за 6 ноября 2022 года. В дальнейшем мы должны обнаружить минимум три связки (неизвестно, есть ли в графе связки, поэтому цены в трех ордерах были намеренно изменены).
Python
edges = [
('BTC', 'USDT', {'price': 21217.93, 'type': 'b'}),
('USDT', 'BTC', {'price': 21221.27, 'type': 's'}),
('BTC', 'ETH', {'price': 0.076249, 'type': 's'}),
('ETH', 'BTC', {'price': 0.076202, 'type': 'b'}),
('XRP', 'BTC', {'price': 0.000022, 'type': 'b'}),
('BTC', 'XRP', {'price': 0.000023, 'type': 's'}),
('MANA', 'BTC', {'price': 0.000026, 'type': 'b'}),
('BTC', 'MANA', {'price': 0.000033, 'type': 's'}),
('TON', 'BTC', {'price': 0.000078, 'type': 'b'}),
('BTC', 'TON', {'price': 12523.378619, 'type': 'b'}),
('ETH', 'USDT', {'price': 1617.69, 'type': 'b'}),
('USDT', 'ETH', {'price': 1618.2, 'type': 's'}),
('MANA', 'ETH', {'price': 0.000432, 'type': 'b'}),
('ETH', 'MANA', {'price': 0.000433, 'type': 's'}),
('ETH', 'TON', {'price': 952.658952, 'type': 'b'}),
('TON', 'ETH', {'price': 0.001031, 'type': 'b'}),
('ETH', 'NEO', {'price': 0.00553, 'type': 's'}),
('NEO', 'ETH', {'price': 0.00551, 'type': 'b'}),
('MKR', 'ETH', {'price': 0.551, 'type': 'b'}),
('ETH', 'MKR', {'price': 0.554, 'type': 's'}),
('XRP', 'USDT', {'price': 0.48806, 'type': 'b'}),
('USDT', 'XRP', {'price': 0.48807, 'type': 's'}),
('BCH', 'TON', {'price': 70.262373, 'type': 'b'}),
('TON', 'BCH', {'price': 0.013619, 'type': 'b'}),
('BCH', 'MANA', {'price': 174.81468, 'type': 'b'}),
('MANA', 'BCH', {'price': 0.005675, 'type': 'b'}),
('BCH', 'NEO', {'price': 13.665698, 'type': 'b'}),
('NEO', 'BCH', {'price': 0.071725, 'type': 'b'}),
('BCH', 'MKR', {'price': 0.136274, 'type': 'b'}),
('MKR', 'BCH', {'price': 7.251667, 'type': 'b'}),
('BCH', 'USDT', {'price': 122.4, 'type': 'b'}),
('USDT', 'BCH', {'price': 122.5, 'type': 's'}),
('BCH', 'EOS', {'price': 108.494334, 'type': 'b'}), # 105.494334 -> 108.494334
('BCH', 'ETH', {'price': 0.075618, 'type': 'b'}),
('ETH', 'BCH', {'price': 13.164972, 'type': 'b'}),
('BCH', 'BTC', {'price': 0.00577, 'type': 'b'}),
('BTC', 'BCH', {'price': 0.00578, 'type': 's'}),
('MKR', 'BTC', {'price': 0.042, 'type': 'b'}),
('BTC', 'MKR', {'price': 23.6496, 'type': 'b'}),
('MKR', 'EOS', {'price': 767.717826, 'type': 'b'}),
('EOS', 'MKR', {'price': 0.00123, 'type': 'b'}),
('MKR', 'TON', {'price': 486.493201, 'type': 'b'}),
('TON', 'MKR', {'price': 0.001736, 'type': 'b'}),
('MKR', 'MANA', {'price': 1291.66985, 'type': 'b'}), # 1271.66985 -> 1291.66985
('MANA', 'MKR', {'price': 0.000779, 'type': 'b'}),
('MKR', 'NEO', {'price': 99.53889, 'type': 'b'}),
('NEO', 'MKR', {'price': 0.009954, 'type': 'b'}),
('USDT', 'NEO', {'price': 0.111549, 'type': 'b'}),
('NEO', 'USDT', {'price': 8.91, 'type': 'b'}),
('USDT', 'MANA', {'price': 1.430278, 'type': 'b'}),
('MANA', 'USDT', {'price': 0.7017, 'type': 'b'}),
('USDT', 'TON', {'price': 0.58084, 'type': 'b'}),
('TON', 'USDT', {'price': 1.679, 'type': 'b'}),
('USDT', 'EOS', {'price': 0.861175, 'type': 'b'}),
('EOS', 'USDT', {'price': 1.1581, 'type': 'b'}),
('USDT', 'BCH', {'price': 0.008145, 'type': 'b'}),
('BCH', 'USDT', {'price': 122.4, 'type': 'b'}),
('MANA', 'NEO', {'price': 0.077892, 'type': 'b'}),
('NEO', 'MANA', {'price': 12.730733, 'type': 'b'}),
('TON', 'NEO', {'price': 0.195311, 'type': 'b'}), # 0.175311 -> 0.195311
('NEO', 'TON', {'price': 5.139507, 'type': 'b'}),
('TON', 'MANA', {'price': 2.3448, 'type': 'b'}),
('MANA', 'TON', {'price': 0.411988, 'type': 'b'}),
('TON', 'EOS', {'price': 1.418086, 'type': 'b'}),
('EOS', 'TON', {'price': 0.67152, 'type': 'b'})
]
Сначала следует разобраться, что именно для нас "метричность" и "оптимизационность". Задача крайне похожа на поиск кратчайшего пути в графе, но в нашем случае мы измеряем не расстояния, а доходности, которые вычисляются через умножение, а не сложение. Причем критерием оптимальности является не наименьшее, а наибольшее значение измеряемой величины. Исправить ситуацию с заменой умножения на сложение поможет обычное логарифмирование. Чтобы после такого преобразования наименьшая сумма соответствовала наибольшему произведению, логарифм должен быть взят от значений, обратных указанным ценам:
Python
edges_log = []
for i in edges:
if i[2]['type'] == 'b':
edges_log.append((i[0], i[1], {'weight': np.log(1 / i[2]['price']),
'price': i[2]['price'],
'type': i[2]['type']}))
else:
edges_log.append((i[0], i[1], {'weight': np.log(i[2]['price']),
'price': 1 / i[2]['price'],
'type': i[2]['type']}))
Теперь можно создать граф и взглянуть на него:
Python
# Создаем граф:
DG = nx.DiGraph()
DG.add_edges_from(edges_log)
Рисуем граф
f, ax = plt.subplots(figsize=(5, 5))
pos = nx.circular_layout(DG)
nx.draw_networkx(DG, pos=pos, node_size=1500,
font_color='w',
font_weight='semibold',
font_size=10, ax=ax)
nx.draw_networkx_nodes(DG, pos=pos, node_size=1500,
node_color='teal',
edgecolors='k', ax=ax);
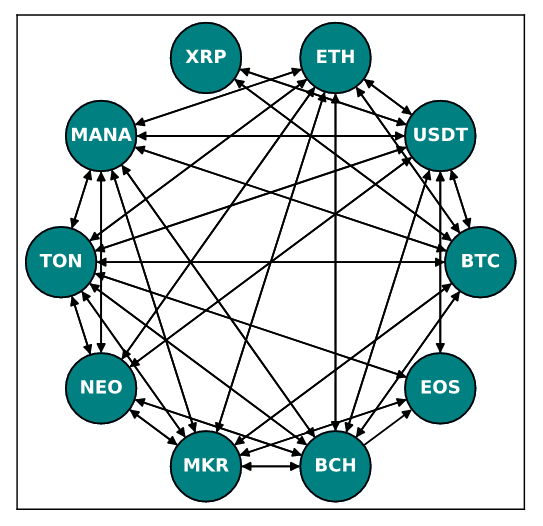
Поиск кратчайшего пути между двумя вершинами в таком графе эквивалентен поиску наиболее прибыльной последовательности обменов. Найдем кратчайший путь между двумя смежными вершинами: если кратчайший путь не проходит через инцидентную этим двум вершинам дугу, то благодаря данной дуге найденный путь может быть достроен до цикла. Если после достраивания доходность оказалась приемлемой, значит мы нашли подходящую связку. Найдем кратчайший путь между вершинами MANA и TON:
Python
list(nx.all_shortest_paths(DG, 'MANA', 'TON',
weight='weight',
method='bellman-ford'))[0]
Результат
NetworkXUnbounded: Negative cost cycle detected.
Вместо кратчайшего пути мы получили сообщение об ошибке - алгоритм обнаружил цикл отрицательной стоимости, не позволяющий ему завершить свою работу. Хорошая новость здесь в том, что цикл отрицательной стоимости - это и есть связка, а плохая - ее обнаружение не является контролируемым процессом.
Может быть, алгоритм Беллмана-Форда - это тупик? Однако более перспективных способов поиска цепочек, увы, не существует.
Обозначим количество циклов в графе символом . В наихудшем сценарии, когда граф является полносвязным (т.е. каждая вершина связана со всем остальными), количество циклов может быть определено по следующей формуле:
Для полносвязного графа это количество не так уж велико:
Python
def prod(l):
p = 1
for i in l:
p *= i
return p
n = 10
sum([prod(range(n, k, -1))//(n - k) for k in range(n-2, -1, -1)])
Результат
1112073
К тому же, это количество циклов в полносвязном графе , у которого должно быть 90 дуг, в нашем графе их всего 66. Так что и циклов будет всего 30444. Удивительным является тот факт, что благодаря некоторым приемам предварительной сортировки мы можем довести перебор циклов до вполне рабочего состояния.
Рассмотрим алгоритм Беллмана-Форда (АБФ) еще раз, но уже более детально. АБФ позволяет находить длины кратчайших путей от некоторой вершины графа до всех остальных. На практике результат его работы оказался для нас бесполезным.
Что насчет самого механизма его работы? Основой АБФ является динамическое программирование: для оптимизации на текущем шаге используются результаты оптимизации шага предыдущего. Именно поэтому некоторые выстраиваемые на каждом шаге кратчайшие пути рано или поздно могут попасть в циклы отрицательной стоимости. С точки зрения оптимизации непрерывное перемещение по таким циклам позволяет бесконечно уменьшать длину пути.
Вполне разумно предположить, что если в графе существует несколько циклов отрицательной стоимости, то мы обязательно должны попасть наиболее "отрицательный":
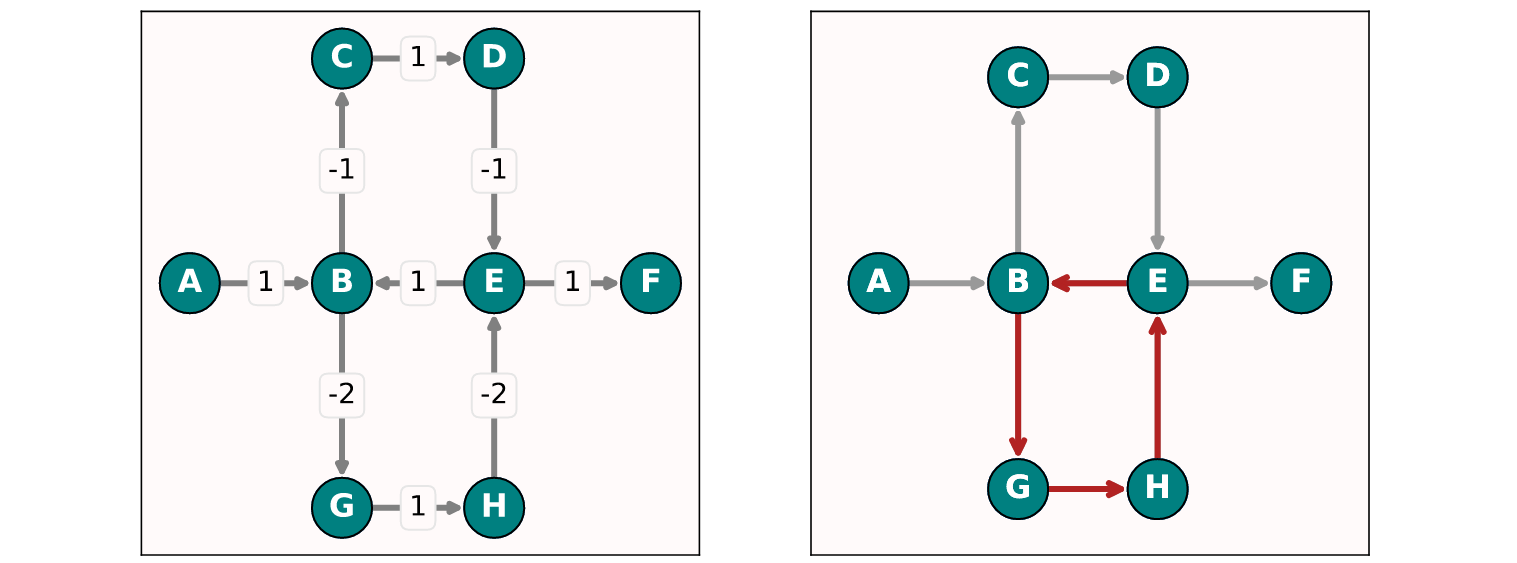
Для графов с небольшой связностью, в которых есть несколько циклов, этого может и не произойти (при условии, что эти циклы могут быть разделены без разрывов). В этом случае мы обнаружим, что разные пути будут попадать в разные циклы:
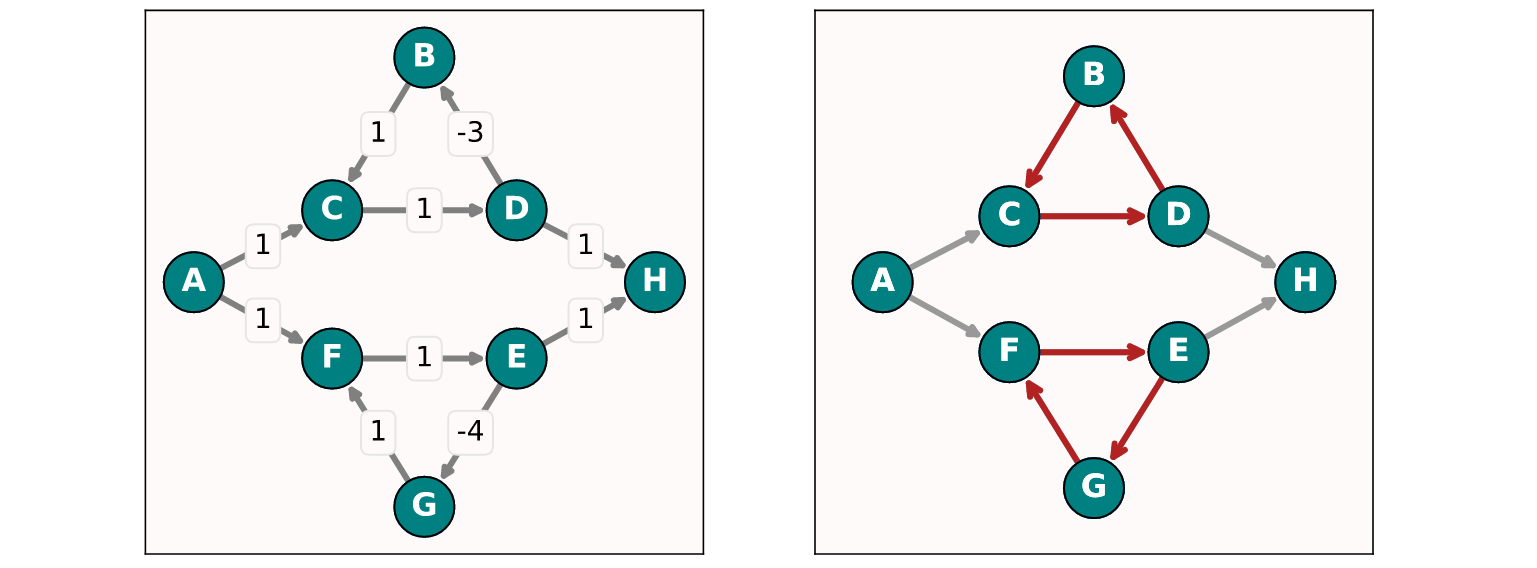
Для графа с большой связностью, когда из каждой вершины можно попасть в любую другую по 1-2 дугам, мы обнаружим, что все пути будут попадать лишь в один цикл, имеющий наименьшую отрицательную стоимость:
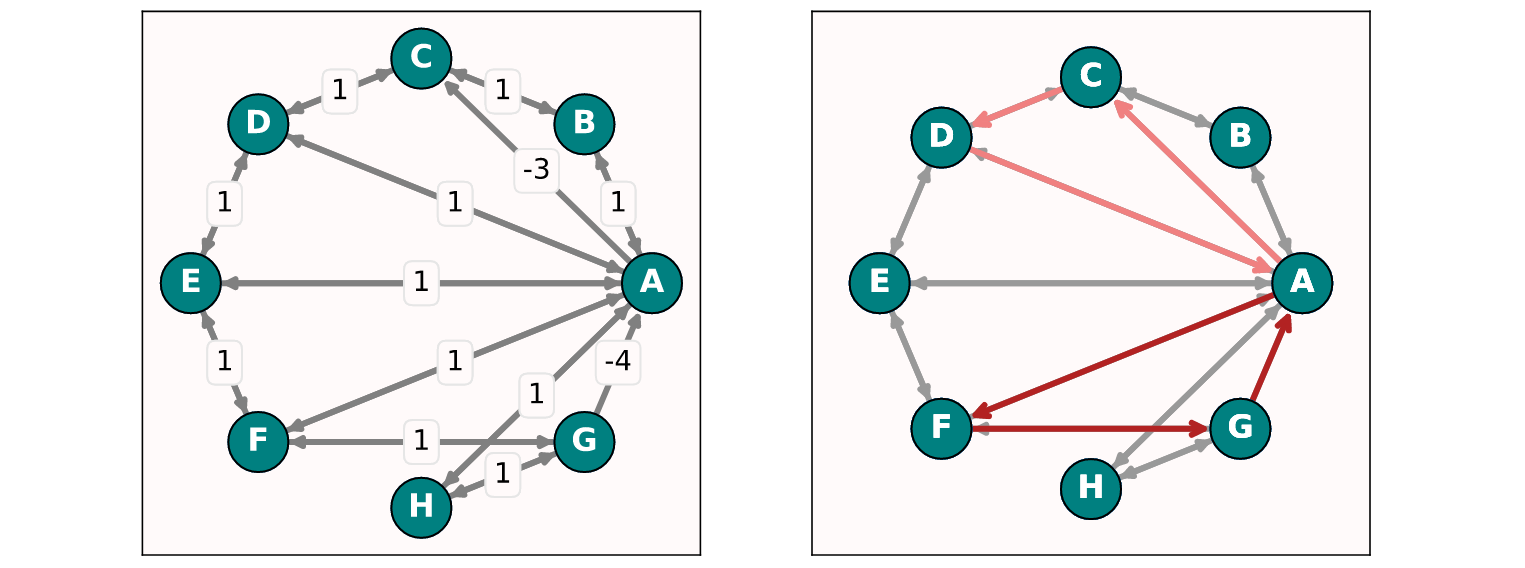
Если обычно для обнаружения отрицательных циклов требуется (
- количество вершин) итераций внешнего цикла АБФ, то для графов большой связности может потребоваться не более
итераций, где
- количество дуг в цикле. Так как цикл отрицательной стоимости в таком графе достижим из каждой вершины, то и применять алгоритм нужно всего лишь один раз, что является очевидным плюсом.
Используя принцип динамического программирования, лежащий в основе АБФ, мы можем очень быстро находить самую прибыльную связку, но, к сожалению, всего одну. Чтобы обнаружить остальные, следует использоватьалгоритм Йена: поочередно удалять дуги графа, принадлежащих найденному циклу наименьшей отрицательной стоимости. Однако перед тем как удалить следующую дугу, мы будем возвращать на место предыдущую. Есть при этом важный нюанс: в графе из предыдущего примера есть два цикла отрицательной стоимости - AFG со стоимостью равной -2 и ACD со стоимостью -1. Если из графа удалить ребро (A, F) или (F, G), которые принадлежат циклу AFG, то это приведет к тому, что алгоритм по-прежнему будет возвращать цикл AHG с отрицательной стоимостью, равной -2. И только после удаления дуги (G, A), алгоритм вернет цикл ACD.
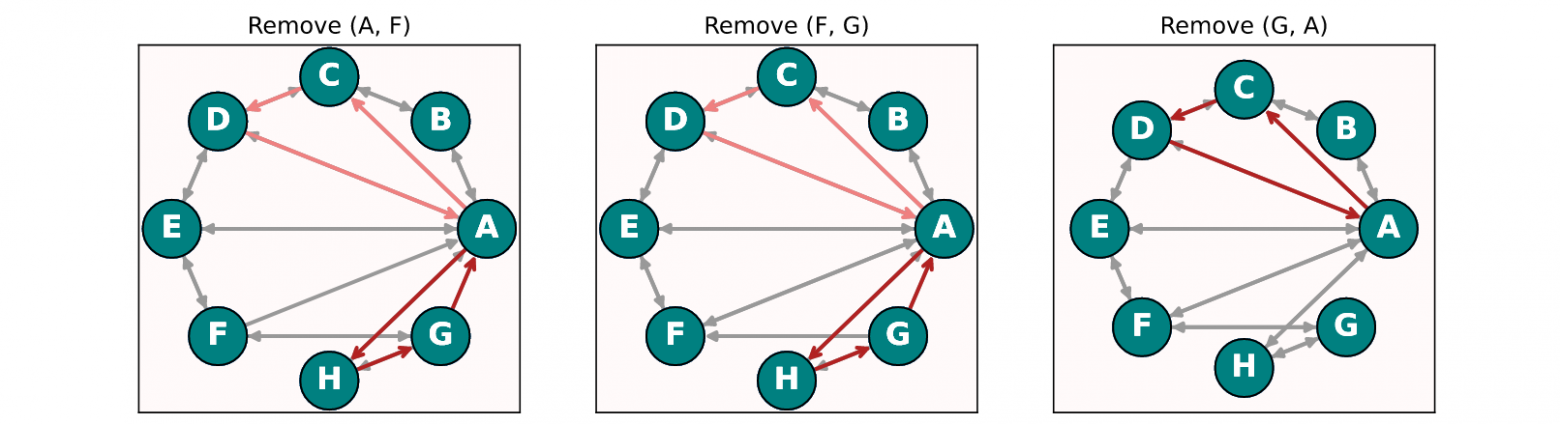
Очевидно, что удаление разных дуг приводит к разным результатам. Некоторые дуги с отрицательным весом можно назвать образующими, так как они позволяют создать целое подмножество циклов отрицательной стоимости. Все циклы в этом множестве будут содержать эту дугу. Цикл наименьшей отрицательной стоимости в этом множестве можно считать основным. Чтобы найти все основные циклы, нужно удалять из графа лишь те дуги, которые являются образующими.
Теперь мы можем создать две простые функции. Первая функция будет выявлять циклы в последовательности вершин выстраивамых путей:
Python
def find_cycle(path):
path_i = path
target = path[-1]
num_occs = {}
for node in path_i:
if node in num_occs:
num_occs[node] += 1
if num_occs[node] == 4:
idx = [path_i.index(node)]
for i in range(3):
idx.append(path_i[idx[-1]+1:].index(node) + idx[-1] + 1)
if path_i[idx[1] : idx[2]] == path_i[idx[2] : idx[3]]:
cycle_i = path_i[idx[1] : idx[2]] + [node]
return cycle_i
break
else:
num_occs[node] = 1
return False
Вторая будет строить кратчайшие пути из указанной вершины во все остальные, используя динамическое программирование:
Python
def bf(DG, target):
N = len(DG.nodes)
preds = [target]
dist = {n: np.inf if n != preds[0] else 0 for n in DG.nodes}
path = {n : [] for n in DG.nodes}
cycle = {n: False for n in DG.nodes}
for i in range(N+10):
succs = set()
for pred in preds:
for succ in DG.successors(pred):
if DG.edges[pred, succ]['weight'] + dist[pred] < dist[succ]:
dist[succ] = DG.edges[pred, succ]['weight'] + dist[pred]
path[succ] = path[pred]+[pred]
c = find_cycle(path[succ])
if c:
cycle[succ] = tuple(c)
succs.add(succ)
preds = succs
if all(cycle.values()):
break
cycle = list(set(cycle.values()))[0]
return dist, cycle, path
Данная функция нуждается в нескольких комментариях. Во-первых, в отличии от АБФ, тут используется результат оптимизации не только с предыдущей итерации внешнего цикла, но и внутреннего. Это позволяет быстрее попадать в циклы отрицательной стоимости. Во-вторых, мы ищем эти циклы, а не пытаемся ответить на вопрос о том, есть они в графе или нет. Это значит, что если в графе имеется N вершин, то для небольших графов будет недостаточно N итераций внешнего цикла. Так что если функция не выдает циклов, то можно увеличить количество итераций.
Создадим еще одну функцию для вычисления доходности связки:
Python
def prod_cycle(cycle):
prices_i = []
for i in range(len(cycle)-1):
prices_i.append(DG.edges[cycle[i], cycle[i+1]]['price'])
print(round((np.array(prices_i).prod() - 1)*100, 2), '%')
Python
# Создаем граф:
DG = nx.DiGraph()
DG.add_edges_from(edges_log)
Попробуем найти связку:
Python
cycle = bf(DG, 'ETH')[1]
cycle
Результат
('TON', 'NEO', 'ETH', 'TON')
Детально найденная связка выглядит следующим образом:
доходность которой равна 2.52%:
Python
prod_cycle(cycle)
Результат
2.52 %
Дуга (TON, NEO) является образующей для данного цикла. Если попытаться составить короткую связку с данной дугой:
то ее доходность получится очень маленькой:
Python
prod_cycle(('TON', 'NEO', 'TON'))
Результат
0.38 %
Образующая дуга может восприниматься как сделка, в которой актив либо недооценен, либо переоценен.
Удалим образующую дугу из графа:
Python
# создаем копию графа:
T = DG.copy()
# удаляем ребро
T.remove_edge('TON', 'NEO')
И попробуем отыскать еще связку:
Python
cycle = bf(T, 'ETH')[1]
cycle
Результат
('USDT', 'BTC', 'BCH', 'EOS', 'USDT')
Мы нашли связку которая состоит из 4-х обменов:
а ее доходность равна 2.44%:
Python
prod_cycle(cycle)
Результат
2.44 %
Образующая дуга вовсе не обязана иметь наименьший вес в цикле. В данном случае мы точно знаем, что образующей цикл дугой является дуга (BCH, EOS), хотя ее вес равен -4.69, в то время как вес дуги (BTC, BCH) равен -5.15. Поскольку в графе отсутствует дуга (EOS, BCH), то у нас не получится составить короткую связку с образующей дугой (BCH, EOS). Однако мы можем сократить данную связку до трех обменов:
доходность которой лишь незначительно уменьшится до 2.34%:
Python
prod_cycle(('USDT', 'BCH', 'EOS', 'USDT'))
Результат
2.34 %
Удалим образующее ребро и поищем еще:
Python
# удаляем ребро
T.remove_edge('BCH', 'EOS')
# ищем цикл:
cycle = bf(T, 'ETH')[1]
cycle
Результат
('MKR', 'MANA', 'MKR')
Мы нашли короткую связку, состоящую всего из 2-х обменов:
Но доходность связки довольно низкая, всего 0.62%:
Python
prod_cycle(cycle)
Результат
0.62 %
Теоретически, мы должны были найти всего три связки, ведь в данных по ордерам изменения вносилось только в три из них. Однако нам уже второй раз попадается дуга (MANA, USDT). Может быть она тоже является образующей? Проверим это:
Python
T.remove_edge('MKR', 'MANA')
И выполняем поиск:
Python
cycle = bf(T, 'ETH')[1]
cycle
Результат
('USDT', 'MANA', 'USDT')
Действительно, у нас удалось найти еще одну связку:
которая, как оказалось, находилась там еще до внесения изменений в цены ордеров.
Доходность связки небольшая и составляет всего 0.36%:
Python
prod_cycle(cycle)
Результат
0.36 %
Больше в данном графе никаких циклов отрицательной стоимости не существует:
Python
# удаляем ребро
T.remove_edge('MANA', 'USDT')
# ищем цикл:
cycle = bf(T, 'ETH')[1]
cycle
Результат
Если взглянуть на найденные связки, то можно подумать, что каждая из них может быть образующей:

Вполне возможно, что если взять ордера по всем остальным валютам и добавить их в граф, то так и окажется. Но именно для данного графа это не так. Все дело в том, что чаще всего нельзя точно установить какой именно актив имеет явную переоценку или недооценку. По большей части активы имеют, так сказать, немного несправедливые цены, которые могут накладываться друг на друга в процессе обменов. Поэтому, несмотря на существование сотен криптовалютных пар на спотовом рынке, связок типа практически никогда не бывает (исчезают практически мгновенно). В то время как связок, состоящих из трех и более обменов может быть очень много.
APT предупреждает: арбитраж - это не волшебство
Арбитражная теория ценообразования (arbitrage pricing theory) не отвечает на вопрос, как зарабатывать больше на арбитраже криптовалют. Она скорее утверждает, что рынок не будет допускать арбитража только при наличии некоторого метода рационального прогноза изменения цен. Также утверждается, что рынок при наличии арбитража позволяет зарабатывать без риска и без начального капитала. Звучит как безрисковый способ зарабатывания денег, но так ли это?
Основной причиной возникновения арбитражной ситуации считается незнание чего-то, что имеет влияние на рынок. Это возможно продемонстрировать с помощью уже знакомой нам портфельной теории. В обычной модели оценки финансовых активов основная идея заключается в том, что доходность портфеля должна как-то коррелировать с доходностью всего рынка:
где - это доходность получаемая сверх рынка, которая должна быть как можно больше.
В теории арбитражного ценообразования используется иной подход:
Понятие единого рынка заменяется совокупностью факторных портфелей. В нашем случае, такими факторами могут быть: начальные криптовалюты в связках и принадлежность этих валют к определенным категориям. Причем считается, что самой по себе альфы не существует. Если же она вдруг появилась, то это означает, что появилась арбитражная ситуация, которая заставляет нас увеличивать объемы активов в портфеле fund и уменьшать долю всех других активов из на величины, пропорциональные их "бетам". С другой стороны, появление альфы свидетельствует о том, что ни мы, ни кто-то еще просто не знает о каких-то факторах. Именно это незнание и порождает арбитражную ситуацию.
Может показаться, что в данном случае для криптоарбитражеров APT не несет никакой пользы. Однако она полезна для инвесторов, так как позволяет понять какие активы надо покупать, а какие продавать. В случае с арбитражем APT позволяет вполне обоснованно предположить, что тот, кто обладает большей информацией, сможет сделать так, что другие, менее информированные участники, будут реже наблюдать появление "альфы" или не наблюдать ее вовсе. Это также означает, что более информированные участники могут производить диверсификацию наиболее эффективным образом и получать дополнительную доходность за счет тех, кто делает это менее эффективно. Более информированный арбитражер будет оказываться в нужном месте в нужное время гораздо чаще, чем неинформированный.
Эффективный рынок является таковым благодаря арбитражу. А просуществует арбитраж, наверняка, еще очень и очень долго. Однако арбитраж криптовалют точно не является волшебством, благодаря которому можно делать деньги из воздуха. Придется столкнуться с большим количеством математики, для того чтобы выжить в этой сфере.
Заключение
На практике наибольшую пользу оказала функция полезности, в особенности возможность оценивать время жизни связок. Диверсификация по криптовалютам же оказалась практически бесполезной для нас - возможно, более заметный положительный эффект можно заметить только при очень больших объемах средств. В то же время весьма полезной оказалась диверсификация и перебалансировка по биржам: рост доходности оказался именно таким, как мы и предполагали - в интервале от 30% до 80%. Рост доходности в большей мере оказался связан с ростом эффективной работой самих арбитражеров, чем с ростом доходности самих связок.
Иногда благодаря заметному снижению количества действий, необходимых для прокрутки по связкам, а также параллельным обменам на разных биржах удавалось прокручивать средства по довольно длинным цепочкам с доходностью гораздо больше обычного. В дальнейшем на проработке именно такой стратегии арбитража мы и хотим сконцентрировать наши усилия.