Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
Упомянутая в заглавии книга (далее H&H) - это про железо [15]. Я - про программирование, но на базе "железной модели" конечного автомата. И там и там математическая основа одна. Все это, действительно, крутая железная концепция, помогающая поставить не только синтез цифровых схем, но и программирование на совершенно другие рельсы, определяющие его будущее.
Параллелизм у программистов нынче в моде. Но, видимо, они (программисты) совсем не в курсе, что разработчики железа давным-давно погружены в эту тему. А потому им (я все про программистов) есть у кого поучиться. Но, похоже, некие амбиции-заскоки этому мешают. Но, если вы этим не страдаете, то прочитайте книгу H&H и дойдите, ну, хотя бы до 4-й главы. Попробуйте реализовать одно-два упражнения, используя свой, программистский инструментарий - всякие там корутины, потоки и весь сопутствующий этому террариум. Убедитесь в его полном бессилии. И тогда, может, это заставит кое-что пересмотреть, переосмыслить. Только представьте: логический элемент - отдельный процесс, десятки, сотни, тысячи элементов - множество параллельных процессов, и все это в вашей ладошке (это я про смартфон) и даже работает!
Но пришло время исполнять обещанное (см. предыдущую часть темы в [1]). И пусть количество "плюсов" пока не достигло заданной планки, но ... если каждый "минус" считать за два "плюса", то это уже более чем ... ;) Так что спасибо всем, давшим положительную оценку - нет, не автору, а затронутой теме. Области знаний, от которой многое сейчас зависит. Это те слова, которые мы вправе сказать в адрес теории, посвященной синтезу цифровых схем, в адрес тех, кто занимался и занимается ее развитием, становлением и внедрением в практику.
И не надо забывать, что именно наши ученые, особенно советской школы, внесли в ее развитие свой значимый вклад. И, может, следовало бы дополнить книгу хотя бы небольшим обзором, отражающим этот факт. А так может создаться впечатление, что мы к этому имеем лишь косвенное отношение и даже в большей степени, как потребители. Ведь, даже учебник для себя сами написать не можем. Хотя это совсем не так... Были и есть учебники, был и есть вклад... Просто все немного подзабылось.
В основе проектирования цифровых схем лежит теория, базирующаяся на двух моделях цифровых схем - комбинационной и последовательностной. В первой части мы рассмотрели комбинационные схемы, эту же часть посвятим больше последовательностной модели. Эти же две темы определяют основу книги H&H, т.к. именно на них базируется рассмотрение всего остального - от приемов и подходов к реализации схем до языков описания аппаратуры.
Светофор
Комбинационная модель - грубая модель, которая не учитывает временных свойств цифровых элементов. Но она проста и легко аппроксимируема понятиями теории булевых функций [2]. Это позволяет выполнять процедуры оптимизации схем, что достаточно подробно описано в научной литературе. Особенно в советской. И еще давно. А были, ведь, "богатыри"!
Но легкость манипулирования булевыми функциями создает ложное представления о модели логических элементов. Формируются даже определенные мифы. И об одном из них мы ниже подробно поговорим. Ну, а пока перейдем к задаче, которая в книге Н&Н приведена для знакомства со второй моделью цифровых схем - последовательностной. Речь пойдет о задаче проектирования системы управления (СУ) простого светофора.
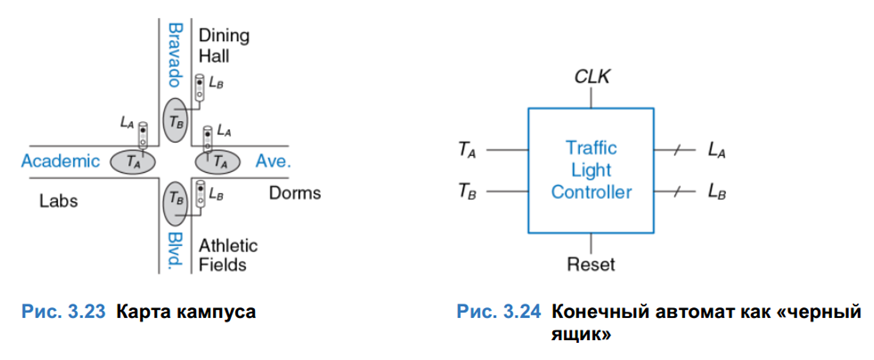
Создание СУ было поручено уже знакомому нам по книге студенту Бену Битдидлу, которой незамедлительно взялся за дело. Что послужило причиной такого задания подробно описано в разделе 3.4.1 книги H&H. Исходные данные для проектирования, место расположения светофоров и структурная модель системы управления показаны на рис. 1.
В соответствии с заданием Бен установил на перекрестке два датчика - Ta и Tb. Они фиксируют движение по улицам. Управлять сигналами светофоров предполагается двумя сигналами La и Lb. Для формирования пауз между переключениями Бен решил тактировать СУ импульсами раз в 5 сек. По переднему фронту импульса светофоры должны гореть в зависимости от состояния датчиков движения. Не была забыта и кнопка сброса светофора.
Граф модели СУ (в книге он почему-то назван таблицей), который нарисовал Бен, показан на рис. 2. И сразу потекли вопросы. Возьмем форму графа. Если уж мы привлекли теорию автоматов, то желательно использовать описание, отвечающее принятым в ней нормам. Как это может выглядеть показано на рис. 3 и рис. 4. Здесь показана модель в двух классических вариантах - модели автомата Мура (рис.3), которая напрямую соответствует модели на рис. 2, и эквивалентная ей модель автомата Мили (рис. 4).

Разницу между моделями на рис. 2 и рис. 3 можно описать, как разницу между эскизом детали и конструкторским чертежом. Во-первых, что это за стрелка, направленная откуда-то сверху в состояние S0? Во-вторых, где у автомата начальное состояние? Или этой стрелкой обозначено именно оно? Судя по всему, так оно и есть. Но "конструкторская документация" предусматривает для обозначения этого другие средства. Например, используя иное изображение начального состояния. На рис. 3, 4 начальным состоянием является состояние, имеющее двойные границы.
Все выше сказанное можно посчитать за придирку, но в той или иной форме начальное состояние должно быть обязательно, а не обозначать в его качестве некий "прилет из безвоздушного пространства".


Безусловно, модель автомата будет включать в себя те или иные особенности, связанные с реализацией. На рис. 2 это сигнал сброса Reset, устанавливающий автомат в начальное состояние. Но тогда, если следовать теории, такие же стрелки-переходы нужно направить из каждого состояния в состояние сброса - S0. На практике сброс - это фактически обязательная стандартная процедура, которой не следует "захламлять" модель. В схеме, реализующей автомат, это элементарный сигнал сброса регистра состояний модели (см. в [2] рис. 3.26 (с)).
К примеру, в реализации автоматов на ПЛК функция сброса модели реализована программно. В каждом программном модуле она представлена соответствующей цепью (см. в [3] цепь 1 на рис. 5). В рамках среды ВКПа (что это за среда см. [4]) функция сброса возвращает любой автомат в начальное состояние или в состояние, которое указано в методе FResetAction() (см. ниже код реализации автомата на С++ в ВКпа).
Специфику программной реализации включают и модели на рис. 3, 4. Ей соответствует петля в начальном состоянии st, помеченная предикатом x12 и действием y12. Здесь предикат x12 выполняет проверку условий, обеспечивающих работу автомата, а отвечающее за инициализацию действие y12 создает ссылки на входные/выходные переменные автомата, выполняет инициализацию значений и т.п. Автомат покинет начальное состояние st, когда будут выполнены все процедуры инициализации.
Поясним роль сигнала bType в моделях на рис. 3 и рис. 4. В программной реализации автоматы, изображенные отдельно, объединены в один автомат (для этого достаточно "склеить" их начальные состояния), режим работы которого определяется данной переменной: в режиме автомата Мура bType=0, в режиме автомата Мили bType=1.
В книге H&H приведена аппаратная реализация модели. Программная реализация имеет свою специфику, но и она должна быть максимально приближена к формальной модели. При прочих равных условиях программная реализация многие вопросы решает все же гибче и проще. Единственно в чем она проигрывает - в скорости, но это дело наживное. Выше было сказано про объединение двух автоматов в один. Программная реализация показывает насколько просто это можно сделать. Листинг программы светофора на языке С++ в среде ВКПа, объединяющий две модели автоматов Мили и Мура, выглядит следующим образом:
Hidden text
#include "lfsaappl.h"
class FTraficLights :
public LFsaAppl
{
enum {enNone, enRed, enYellow, enGreen};
public:
void MooreAction();
void FResetActions();
LFsaAppl* Create(CVarFSA *pCVF) { Q_UNUSED(pCVF)return new FTraficLights(nameFsa); }
bool FCreationOfLinksForVariables();
FTraficLights(string strNam);
virtual ~FTraficLights(void);
CVar *pVarStrNameTa;// имя входного датчика Ta
CVar *pVarStrNameTb;// имя входного датчика Tb
CVar *pVarTypeOfFSM;// тип автомата
CVar *pVarTa; //
CVar *pVarTb; //
CVar *pVarLa; //
CVar *pVarLb; //
protected:
int x1(); int x2(); int x3(); int x12();
void y1(); void y2(); void y3(); void y4(); void y5(); void y6(); void y7();
void y8(); void y9(); void y10(); void y12();
};
#include "stdafx.h"
#include "FTraficLights.h"
static LArc TBL_TraficLights[] = {
LArc("st", "st","^x12","y12"),
LArc("st", "S0","x12^x3","y9"),
LArc("st", "S00","x12x3","y4y6y10"),
// Moore's automaton
LArc("S0", "S1","^x1", "--"),
LArc("S1", "S2","--", "--"),
LArc("S2", "S3","^x2", "--"),
LArc("S3", "S0","--", "--"),
// Mealy`s automaton
LArc("S00", "S10","^x1","y3"),
LArc("S10", "S20","--", "y2y8"),
LArc("S20", "S30","^x2","y7"),
LArc("S30", "S00","--", "y4y6"),
LArc()
};
FTraficLights::FTraficLights(string strNam): LFsaAppl(TBL_TraficLights, strNam)
{ FSetMoore(); }
FTraficLights::~FTraficLights(void) { }
void FTraficLights::FResetActions() { LFsaAppl::FResetActions(); }
void FTraficLights::MooreAction()
{
string strState = FGetState();
if (strState=="st") { y1(); y5(); } // none, none
else if (strState=="S0"){ y4(); y6(); } // La=green, Lb=red
else if (strState=="S1"){ y3(); } // La=yellow
else if (strState=="S2"){ y2(); y8(); } // La=red, Lb=green
else if (strState=="S3"){ y7(); } // Lb=yellow
}
bool FTraficLights::FCreationOfLinksForVariables() {
CVar *pVar=nullptr;
pVarTypeOfFSM = CreateLocVar("bTypeOfFSM", CLocVar::vtBool, "");
pVarTa = CreateLocVar("bTa", CLocVar::vtBool, "bTa");
pVarTb = CreateLocVar("bTb", CLocVar::vtBool, "bTb");
string str;
pVarStrNameTa = CreateLocVar("strTa", CLocVar::vtString, "Ta");
str = pVarStrNameTa->strGetDataSrc();
if (str != "") { pVar = pTAppCore->GetAddressVar(str.c_str(), this);
if (pVar) pVarTa = pVar;
}
pVarStrNameTb = CreateLocVar("strTb", CLocVar::vtString, "Tb");
str = pVarStrNameTb->strGetDataSrc();
if (str != "") {
pVar = pTAppCore->GetAddressVar(str.c_str(), this);
if (pVar) pVarTb = pVar;
}
pVarLa = CreateLocVar("nLa", CLocVar::vtInteger, "nLa");
pVarLb = CreateLocVar("nLb", CLocVar::vtInteger, "nLb");
return true;
}
int FTraficLights::x1() { return static_cast<int>(pVarTa->GetDataSrc()); }
int FTraficLights::x2() { return static_cast<int>(pVarTb->GetDataSrc()); }
int FTraficLights::x3() { return static_cast<int>(pVarTypeOfFSM->GetDataSrc()); }
int FTraficLights::x12() { return pVarTa != nullptr && pVarTb; }
void FTraficLights::y1() { pVarLa->SetDataSrc(this, enNone); }
void FTraficLights::y2() { pVarLa->SetDataSrc(this, enRed); }
void FTraficLights::y3() { pVarLa->SetDataSrc(this, enYellow); }
void FTraficLights::y4() { pVarLa->SetDataSrc(this, enGreen); }
void FTraficLights::y5() { pVarLb->SetDataSrc(this, enNone); }
void FTraficLights::y6() { pVarLb->SetDataSrc(this, enRed); }
void FTraficLights::y7() { pVarLb->SetDataSrc(this, enYellow); }
void FTraficLights::y8() { pVarLb->SetDataSrc(this, enGreen); }
void FTraficLights::y9() { FSetMoore(true); }
void FTraficLights::y10() { FSetMoore(false); }
void FTraficLights::y12() { FInit(); }
Листинг 1. Программная реализация модели светофора на С++
Миф об автоматах Мили и Мура
Цитата из H&H. "Существует два основных класса конечных автоматов, которые отличаются своими функциональными описаниями. В автомате Мура выходные значения зависят лишь от текущего состояния, в то время как в автомате Мили выход зависит как от текущего состояния, так и от входных данных." С этим можно было бы согласиться, но...
Процитируем другого классика из классиков[3]. "... Для задания функций выходов (обычной или сдвинутой) ребра графа (стрелки) обозначаются не только входными, но и соответствующими им выходными сигналами. Если обозначенная входным сигналом xi стрелка соединяет вершину aj с вершиной ak, то в случае автоматов первого рода ей приписывается выходной сигнал λ1(aj, xi), а в случае автоматов второго рода - выходной сигнал λ2(ak, xi), где λ1 и λ2 - соответственно обычная и сдвинутая функции выходов автомата.
В случае автоматов Мура все стрелки, входящие в одну и ту же вершину aµ, должны быть обозначены одним и тем же выходным сигналом. Поэтому принято обозначать выходными сигналами не стрелки, а вершины, в которые эти ребра входят".
И это уже ближе к истине: сигналы с дуг убираются и приписываются вершине, в которую они направлены. И если посмотреть на рис. 2, то, вроде бы, противоречий-то и нет. Но они есть, т.к. утверждение, что выходной сигнал автомата Мура зависит только от состояния, которым он помечен, не верно. На самом деле зависит, как и любой сигнал, выдаваемый автоматом Мили. Просто, повторимся, одинаковые выходные сигналы всех переходов, ведущих в одно состояние, приписываются этому состоянию, которое станет текущим только на следующем такте. Т.е. мы имеем скрытую зависимость рассматриваемого выходного сигнала автомата Мура от текущего состояния и тех входных ситуаций, которые вызывают соответствующие переходы. Просто мы схитрили, упростив запись функции выходов автомата Мили, "обозвав" его попутно автоматом Мура. А автомат Мура - это лишь упрощенная запись эквивалентного ему автомата Мили.
В силу сказанного выше мы можем "по щелчку" для любого автомата Мура создать эквивалентный автомат Мили, перенеся сигнал с вершины, на ведущие в нее дуги. Но мы наталкиваемся на проблемы, пытаясь найти эквивалентный автомату Мили автомат Мура. Все это объяснить это можно хотя бы тем, что, рассматривая некий автомат, как "черный ящик", в общем случае невозможно дать ответ о форме его внутреннего представления - это автомат Мили или Мура. Тестирование программной реализации на С++ в рамках ВКПа, представленной на листинге 1, в этом также убеждает: результаты абсолютно одинаковы, а тип автомата можно понять только по значению переменной bType.
Аргументом в пользу развенчания мифа может служить и сравнение результатов программного моделирования схемной реализации автомата на рис.2 (представленна в H&H на рис. 3.26, стр. 318), с программной реализацией автоматов в разных формах (см. листинг 1). Опять же (по крайней мере в рамках ВКПа) их функционирование неотличимо.
Рис. 22 в H&H создает "ложное" представление о независимости сигналов автомата Мура от входных сигналов автомата, т.к., как ни крути, переход в то или иное состояние (кроме начального) у автомата Мура определяется только его текущим состоянием и текущей входной ситуацией на входах (смю выше цитату из книги H&H). Не было бы этих переходов не было бы и последующего состояния и соответственно сигналов автомата Мура.
Тем не менее, форма автоматов Мура имеет свои плюсы даже в сравнении со своим прародителем - автоматом Мили. Например у Мура вместо указания сигнала на каждом переходе он обозначается один раз при состоянии. Это повышает надежность проектирования, т.к. вероятность пропустить/забыть сигнал на переходе, особенно когда их достаточно много, гораздо выше, чем при состоянии. А, например для ПЛК использование автоматов Мура дает даже двойную выгоду. Так, привязав выходной сигнал командой OUT к состоянию, мы автоматически устанавливаем его при входе в это состояние и автоматически же сбрасываем при переходе в другое состояние. Удобно, наглядно, надежно.
Плюсы аппаратной реализации автоматов Мура в сравнении с автоматами Мили (см. рис. 3.22(a)) тоже достаточно давно известны и понятны. Это стабильность выходных сигналов, на которые, действительно, не влияет нестабильностm входных сигналов, формируемых, если следовать терминологии H&H, некой "обезьяной" (см. стр. 348). Последняя в неконтролируемые по отношению к фронту тактового сигнала моменты времени с произвольной частотой изменяет входной сигнал, порождая так называемую метастабильность. Но, еще раз, это совсем не означает, что выходные сигналы автомата Мура не зависят от ситуации, вызвавшей его переход в то или иное состояние.
Надуманность разделения автоматов на две форме можно показать и на других примерах. Например, в достаточно объемной монографии Марвина Минского "Вычисления и автоматы" при активном использовании автоматов почему-то эти две формы не упоминаются [6]. При этом, исходя из времени ее издания, сложно предположить, что он о них не знал. Еще навскидку - книга Дж фон Неймана по самовоспроизводящимся автоматам[7]. Или другая - про клеточные автоматы [8]. В них используются просто автоматы в своей единственной, определяемой формальным описанием, форме.
C формальной точки зрения в автоматах Мура необходимости нет. Они всего лишь подмножество автоматов Мили и покрываются последними. А как же быть с их ролью в схемах с обратными связями (см. [3])? Ведь элемент памяти - классический пример автомата Мура. А никак! В них в этом случае нет нужды, т.к. их заменяют эквивалентные им и, кстати, неотличимые от них автоматы Мили. Правда, для этого необходимо изменить закон функционирования последних, убрав мгновенную зависимость выходных сигналов от входных. Или, говоря другими словами, использовать инерционную форму функции переходов автомата (инерционный закон функционирования автоматов подробно рассмотрен в [4]). Кстати в этом случае исчезает во многом необходимость включать автоматы в разрывы обратных связей.
Сама по себе форма автоматов Мура достаточно удобна, т.к. повышает надежность проектирования, чем в определенных ситуациях ее применение оправдано. Но повторимся, это всего лишь модифицированная форма автомата Мили. А общем случае - просто автомата. Автомата, который известен, как совмещенная форма автоматов Мили и Мура. В теории проектирования цифровых схем ее еще часто называют С-автоматом [9]. Для книги H&H это сводится к совмещению двух структурных схем реализации автоматов в одну схему - совмещение схем (a) и (b) на рис. 3.22.
О форме описания автоматов
Если сравнить автоматы Мура на рис. 2 и рис. 3, то внимательный глаз увидит, что у модели на рис. 3 отсутствуют петли. В них просто нет нужды. От слова совсем. Просто на рис. 3 используется минимизированная форма автомата - дизъюнктивная нормальная форма структурных автоматов (ДНФ СКА), описанная в статье [4].
Более того, синтез цифровой схемы по ДНФ СКА может порождать логические функции, требующие меньших шагов для их минимизации. Например, в нашем случае можно построить следующую таблицу переходов (Табл. 1) (подробнее про таблицы переходов см. [5]), по которой затем провести синтез комбинационной схемы.
Табл.1
Ta, Tb | S0 (00) | S1 (01) | S2 (10) | S3 (11) |
^x1^x2 | S1 (01) | S2 (10) | S3 (11) | S0 (00) |
^x1x2 | S1 (01) | S2 (10) | S3 (11) | S0 (00) |
x1^x2 | S0 (00) | S2 (10) | S3 (11) | S0 (00) |
x1x2 | S0 (00) | S2 (10) | S2 (10) | S0 (00) |
Выражения, построенные по данной таблице, и шаги их минимизации будут выглядеть так:
S0` = ^S1^S0^x1^x2 + ^S1^S0^x1x2 + S1^S0^x1^x2 + S1^S0^x1^x2 = ^S1^S0^x1 + S1^S0^x2
S1` = ^S1S0^x1^x2 + ^S1S0^x1x2 + ^S1S0x1^x2 + ^S1S0x1x2 + S1^S0^x1^x2 + S1^S0^x1x2 +
+ S1^S0x1^x2 + S1^S0x1x2 = ^S1S0^x1 + ^S1S0x1 + S1^S0^x1 + S1^S0x1 = ^S1S0 + S1^S0
Они в точности совпадают с выражениями (3.2) из книги H&H.

На рис. 5 показаны результаты тестирования трех автоматных моделей управления светофоров: в форме автоматов Мура, Мили и цифровой схемы, реализующей автомат Бена. На карте кампуса для каждой модели выделена пара светофоров. Можно видеть, что их поведение синхронно и идентично.
По поводу частоты синхронизации. Возможно, как частное решение, предложенное к тому же студентом, демонстрирующее особенности работы автоматов в дискретном времени, оно и имеет право на жизнь. Но, на мой взгляд, лучшим решением будет выбрать частоту синхронизации максимально возможной, а заданные моменты времени отсчитывать таймером. Это будет ближе к реальной практике, да и гибче с точки зрения развития алгоритма светофора. В свете подобной синхронизации вызывают возражение временные диаграммы сигналов, представленные на рис. 3.27 в H&H. Наклонные фронты сигналов при такой частоте выглядят весьма неправдоподобными.
Декомпозиция автоматов
Синтез цифровой схемы, реализующий автомат - есть декомпозиция на множество взаимодействующих автоматов, каждый из которых представляет модель элементарного логического элемента. При этом простейшая автоматная модель любого логического элемента в рамках модели двоичных сигналов - это автомат с двумя состояниями (по числу состояний выхода). Таким образом, для схемы светофора на рис. 3.26 результат синтеза исходного автомата светофора на рис. 3 - это декомпозиция на девять взаимодействующих автоматов, каждый из которых имеет два состояния.
Обратная операция по отношению к операции декомпозиции - операция композиции автоматов. С ее помощью для некоторого множества автоматов (такое множество в теории автоматов называется сетью автоматов или просто сетью) можно найти эквивалентный однокомпонентный автомат. В нашем случае это должен быть автомат на рис. 3. Немного подробнее о данных операциях (особенно про операцию композиции), которые часто ассоциируются с известными операциями деления и умножения, говорится в статье [4].
Синтез цифровой схемы автомата - это интуитивно найденный подход к декомпозиции исходной модели на некое множество простейших автоматов. Посмотрим, что мы можем получить, если проведем декомпозицию исходного автомата на некое другое множество автоматов, имеющих в общем случае произвольное число состояний.
Во-первых, сразу возникает вопрос - какое минимальное число автоматов может входить в автоматную сеть, представляющую декомпозицию. Их число определяется достаточно просто - пространство состояний такой сети - произведение состояний компонентных автоматов. Оно должно покрывать, т.е. быть равно или больше, числу состояний исходного автомата. Для светофора с его четырьмя состояниями достаточно двух автоматов по два состояния. Но если хотите разобраться в деталях алгебры автоматов, включающих упомянутые операции, то лучших книг (да не обидятся наши бывшие теперь "не-друзья-партнеры") на тему декомпозиции/композиции автоматов, чем книги советских ученых С.И.Баранова[9] и А.Н.Мелихова [10], я не знаю.
Формально декомпозиция может включать любое число автоматов, как в случае сети, эквивалентной схеме автомата светофора - девять автоматов по два состояния. Здесь важно понимать, что взаимодействие компонентных автоматов сети в конечном итоге определит множество состояний, которое содержит эквивалентный сети автомат.
Минуя теоретические препоны, приведем результат декомпозиции автомата на рис. 3 на два автомата. Пусть это будут автоматы A и B и, как уже сказано, содержащие по два состояния. Такая сеть приведена на рис. 6.

Отличие данной декомпозиции от стандартной в том, что последняя использует типовые логические элементы, а здесь компонентные автоматы нужно еще создать. Программно - нет проблем, а с аппаратной - нужно будет попотеть. Фактически это будет проблема, сравнимая по сложности с реализацией исходного автомата. В этом смысле ПЛМ хороши тем, что фактически содержат набор стандартных логических элементов, из которых, путем их соединения, создается сеть/схема, реализующая поставленную задачу.
К чему мы вообще затронули тему декомпозиции/композиции автоматов? Как минимум, для информации. Чтобы на рассматриваемом примере продемонстрировать действия под "автоматным капотом": какие на самом деле с точки зрения теории автоматов решаются проблемы, когда выполняется процедура синтеза цифровой схемы автомата. Другими словами, синтез - синтезом, а об алгебре автоматов, хотя бы общее представление, необходимо иметь. Авторы книги H&H эти вопросы, вольно или нет, пропустили. Для уровня техникума это еще как-то объяснимо и даже где-то оправдано, но когда речь идет о "вышке", то, на мой взгляд, это уже недостаток. Уж упомянуть-то надо было!
Упражнение 3.29
В процессе обсуждения предыдущей части статьи мы вышли на обсуждение упражнения 3.29 из книги. Меня в нем зацепил довольно нестандартная на мой взгляд постановка - синтез автомата по диаграмме сигналов. Я не припомню, чтобы когда-либо я сталкивался с подобным в литературе по автоматам, которую я штудировал когда-то очень давно. Захотелось попробовать свои силы на решении хотя бы этой задачи. Попробовать, так сказать, пройти собеседование... Получилось, прямо скажем, не так чтобы успешно. Как минимум по времени, затраченного на ее решение. Наверное, собеседование я провалил... :(
Неожиданно обсуждение прошло не без пользы и за это спасибо тем, кто в нем участвовал. Не сразу, но мы все же пришли к определенному решению, хотя недоговоренности остались. Но что-то мне подсказывает, что к итогу нас вывело решение, прилагаемое к книге. И было бы хорошо, чтобы "решебник" был доступен, как и книга, хотя бы в оригинале. Но, с другой стороны, если решение было бы известно, то, скорее всего, самого обсуждения не получилось бы. А так ... все прошло, прямо скажем, достаточно живенько.
Напомним упражнение:

Диаграмма, приложенная к нему, следующая:

Для меня просто очевидно, что решение нужно начинать с конца, т.е. с проектирования автомата. Если есть автомат, то ответы на остальные вопросы будут уже очевидны. Для создания такого автомата у нас почти все есть, а то чего нет мы имеем право додумать. А нет явно одного - не оговорено начальное состояние сигнала A. И это сразу вызывает "наивные вопросы" к авторам упражнения...
Начинаем додумывать: мы можем ввести начальное состояние и из него, в зависимости от текущего значения сигнала A, перейти в состояние "1" или "0", чтобы зафиксировать его значение. Далее совсем просто: мы переключаемся из состояния, которое отражает предыдущее значение сигнала A, в состояние, которое соответствует текущему значению сигнала A, а в процессе переходов выдаем сигнал Z в соответствии с логическими уравнениями. Полученный в результате таких размышлений автомат показан на рис. 7.

Автомат создан и, казалось бы, что еще надо? Подаем на входы автомата сигналы A и B и смотрим на выходе сигнал Z. Но не тут-то было...
Какая связь между автоматом на рис. 7, да, и вообще любым другим предполагаемым автоматом, синхросигнала CLK? Да, ни какой (но это только мое мнение)! Но, ведь, зачем-то диаграмма тактового сигнала включена в общую диаграмму. Зачем? И это уже опять вопрос к авторам книги... Но именно диаграмма сигнала CLK осложнила выработку общего решения и внесла диссонанс в процесс обсуждения.
Тем не менее, удалось получить доступ к авторскому решению. Автомат из него приведен на рис. 8. Не станем его комментировать, но зато есть на что обратить внимание. В этом автомате, что примечательно, отсутствует какая-либо привязка к сигналу CLK. Поэтому повторяем вопрос - зачем он присутствует в условии на диаграмме? Думаю, что такое острое внимание к синхросигналу послужило бы причиной отрицательного решения по результату моего собеседования :( А я бы не отстал ;)

Тем не менее, мы можем ввести синхросигнал в автомат и результат такого решения представлен на рис. 9. Диаграммы сигналов, приведенные на рис. 10, показывают его влияние на сигнал Z. Заметим, что "жесткой" установкой сигнала CLK (точнее - предиката x3) в единицу (CLK = 1) мы приводим автомат на рис. 9 к автомату на рис. 7, а значение CLK = YES - к режиму работы автомата на рис. 9.


Нужно также обратить внимание на петли у автоматов на рис. 7 и рис. 9. Они здесь обязательны, т.к. есть переходы с установкой прямо противоположного значения сигнала Z. Это сигнал y2 на переходе в состояние "1" и сигнал y1 на переходе в состояние "0". Если бы их не было, то петли можно было бы без проблем исключить из описания автоматов.
6. Заключение
Может, я ослабил контроль за автоматами, особенно в программировании, но пролистав статьи, в первую очередь на Хабре, обнаружил достаточно заметное число статей на тему автоматов даже за прошедший год. Явно есть большой интерес к данной теме. И мне это понятно, т.к. для меня альтернативы автоматам в программировании давно уже просто нет. Но, на мой взгляд, все или в основном почти все статьи и комментарии к ним отражают весьма простой, если не сказать - примитивный уровень проникновения в автоматы. Но, однако, давайте "полистаем" ...
Вот статьи одного автора [11, 12]. Это вводный материал в тему минимального начального уровня. Чувствуется практический интерес к автоматам. Но... SWICH-технология? Даже много SWICH-технологии. Однако, на дворе 2023 год и вот-вот будет 2024-й, а это совсем не 1998 год - год издания книги А.А.Шалыто. Нынче она (SWITCH-технология) имеет отношение к автоматам, как лето к зиме: времена года, но общего мало. Тем не менее, спасибо А.А.Шалыто за подвижническую деятельность и активную рекламу автоматного программирования. Нынче у SWTCH-технологии общее с автоматным программированием только название (см. подробнее статью [4]). В статье [11], кстати, рассмотрена реализация светофора. Поэтому есть с чем сравнить. А статья [12] содержит включения из книги H&H. Приятная встреча! Правда, без ссылок на первоисточник, но мы этот непорядок исправляем. Есть в ней, кстати, даже ссылка на мою статью. А это еще приятнее, т.к. мой труд, похоже, не пропадает даром :) Но моя критика SWITCH-технологии автором явно не понята. В этом смысле его совет изучить SWICH-технологию только расстраивает...
Статья [13]. Дает краткое представление о применении теории автоматов. Она заточена под оптимизацию цифровых схем, полученных процедурой синтеза автомата. Весьма специфичная тема и, думаю, будет интересна только математикам, занимающихся теми же генетическими алгоритмами. Может ошибаюсь, но полагаться на результаты подобной оптимизации, думаю, будет сложно. По мне так больше интересны комментарии к ней в части обсуждения проблем параллелизма. Какая же каша в головах!
А вот пример большого разговора на тему автоматов на YouTube [14]. Лично я в этом видео мало что понял. Отстал, наверное, или текучка заела. Но как инфа данное видео может кому-то понравится, а что-то (правда, признаюсь, я не знаю что) даже пригодится. Да, чуть не забыл, книга А.А.Шалыто на одном из слайдов доклада все же промелькнула и здесь.
Но в заключение вернем к нашим "баранам"... Посмотрите на рис. 5. Это программный проект, содержащий более 50-ти параллельных процессов. Не однотипных, а весьма разных, взаимодействующих. Из них почти 40 - прикладные. Сюда входят СУ светофора в форме автомата Мили и автомата Мура, логические элементы, объединенные в схему реализации светофора, элементы графического интерфейса и т.д. и т.п. Все это обслуживает с той или иной степенью активности чуть больше десятка процессов ядра ВКПа. И все это - чистые автоматы. Они работают согласованно и дружно решают поставленную задачу/задачи. Это и есть автоматное программирование без изъятий, но здесь ... и близко нет SWITCH-технологии. Подумайте, прочитайте в конце концов, если не читали, статью[4]. Не поняли - перечитайте ее еще раз, еще раз, может, даже еще раз, но включите наконец-то мозги... А то все switch, switch иногда case, if else... Это все и всегда будет про блок-схемы, а не про автоматы...
Литература
1. Не спеши, Маша! Разбор примеров из книги Харрисон Д.М., Хариссон С.Л. Цифровая схемотехника и архитектура компьютера.
2. Проектирование цифровых вычислительных машин. Под ред. С.А. Майорова. Учебное пособие для студентов вузов. - М.: «Высшая школа», 1972. – 344 с.
3. Глушков В.М. Синтез цифровых автоматов. М.: Физматгиз, 1962.
4. Автоматное программирование: определение, модель, реализация. [Электронный ресурс], Режим доступа: https://habr.com/ru/articles/682422/ свободный. Яз. рус. (дата обращения 21.11.2023).
5. Проектирование цифровых вычислительных машин. Под ред. С.А. Майорова. Учебное пособие для студентов вузов. - М.: «Высшая школа», 1972. – 344 с.
6. Минский М. Вычисления и автоматы. М.: Мир, 1971. – 364 с.
7. Джон фон Нейман. Теория самовоспроизводящихся автоматов. М.: Мир, 1971 – 382с.
8. Тоффоли Т., Марголус Н. Машины клеточных автоматов: Пер. с англ. – М.: Мир, 1991. – 280 с.
9. Баранов С.И. Синтез микропрограммных автоматов. -Л.: Энергия, 1979. -232с.
10. Мелихов А.Н. Ориентированные графы и конечные автоматы. – М.: Наука, 1971. – 416 с.
11. OldFashionedEngineer. На полпути к конечному автомату для Arduino. Однопроходные функции и фиксация событий программы с помощью флагов. https://habr.com/ru/companies/timeweb/articles/719376/
12. OldFashionedEngineer. С чем едят конечный автомат. https://habr.com/ru/companies/timeweb/articles/717628/
13. Efi-fi. Оптимизация цифрового автомата (FSM). https://habr.com/ru/articles/530414/
14. Кирилл Мокевнин, Конечные автоматы как способ значительно упростить логику и понимание кода. https://www.youtube.com/watch?v=knoVv2ncwVI
15. Хэррис Д.М., Хэррис С.М. Цифровая схемотехника и архитектура компьютера. - 2-е изд.
PS
Когда уже практически закончил свой мини-обзор, то на YouTube обнаружил канал - Школа синтеза цифровых схем (https://www.youtube.com/@chipdesignschool). Что сказать? - Молодцы и спасибо за выложенные видео! Есть, что изучать, с чем знакомиться и, возможно, даже ... критиковать :)