Эффективное геометрическое хеширование пространства признаков для быстрого точного поиска наиболее близких дескрипторов

При решении задачи распознавания лиц в компании Оксаджайл (Oxagile) был разработан новый алгоритм эффективного геометрического хеширования пространства лицевых признаков с целью быстрого поиска двух наиболее близких по косинусному расстоянию лицевых дескрипторов. Разработанный алгоритм обладает той же точностью, что и метод простого перебора и, в то же время, он приблизительно в сто раз быстрее. С более подробным описанием алгоритма можно познакомиться в англоязычном оригинале настоящей статьи.

Введение

В последние годы автоматизированные методы сличения изображений лиц при установлении наличия в базе запрашиваемой персоны стали особенно популярными. И когда в базе лиц очень большое количество изображений, то затрачиваемое время на поиск наиболее похожего изображения лица на фото сличаемой персоны становиться крайне критичным. Проблема быстрой обработки данных базы лиц даже трансформировалась в отдельную область научных исследований. В настоящее время наиболее популярным методом кодирования отличительных черт лица является нейросетевая экстракция соответствующего ему дескриптора — вектора из многомерного пространства характерных лицевых признаков. Такой подход позволяет свести сличение изображений лиц к формальному сравнению дескрипторов с использованием той или иной метрики. В частности, в качестве первого приближения может применяться и обычное Эвклидово расстояние или наоборот, могут использоваться какие-либо экзотические метрики, хотя наиболее употребимой мерой похожести является косинусное расстояние. В любом случае, независимо от способа задания метрики, задача нахождения наиболее похожего изображения лица из заданного множества лиц на изображение лица сличаемой персоны сводится к поиску ближайшей соседней точки в соответствующем метрическом смысле к заданной точке многомерного пространства лицевых признаков. И такая задача может быть абсолютно точно решена методом полного перебора дескрипторов (поиск дескриптора, отвечающего, например, максимальному значению косинусной похожести). При количестве изображений лиц в базе равном M вычислительная сложность алгоритма поиска, очевидно, пропорциональна M. И если M весьма велико, то на полный перебор может уходить слишком много времени, что, порой, неприемлемо. Более того, из-за аппаратных ограничений начиная с некоторых значений M распараллеливание алгоритма поиска и перенос его на GPU перестает быть эффективным методом ускорения этого алгоритма. Естественным способом решения данной проблемы является специальная организация данных в базе (диаграмма Вороного, K-d-дерево и др.) плюс индексирование, хеширование и пр., позволяющие кардинально ускорить поиск. Конкретных реализаций указанных подходов существует огромное множество. Однако, все они позволяют находить ближайшего соседа либо приблизительно, либо с выделением больших объемов памяти на индексную информацию и большими вычислительными затратами на переиндексацию базы данных.

С учетом вышесказанного возникает естественный вопрос: а вообще возможно ли путем не слишком сложных вычислений без необходимости выделения больших объемов памяти проиндексировать элементы базы так, чтобы впоследствии с помощью некоего специального алгоритма поиска можно было бы абсолютно точно находить ближайшего соседа со среднестатистическим временем поиска, по крайней мере, в разы меньшим, чем время, необходимое на полный перебор элементов в базе. Именно на этот вопрос и отвечает настоящая публикация на примере решения задачи быстрого дескрипторного поиска наиболее похожего изображения лица из базы на изображение лица сличаемой персоны.

Теория

В качестве методологической основы для индексации состоящей из дескрипторов базы изображений лиц используем ряд модификаций такого известного классического алгоритма, как метод геометрического хеширования. Итак, пусть дескриптора d_ij — это элементы векторного пространства лицевых признаков единичной длины с размерностью N = 512 (но может быть больше или меньше), извлекаемые из изображений лиц какой-либо нейронной сетью, например, типа ArcFace с бэкбоном типа ResNet, которая была обучена, например, с использованием WiderFace.

Геометрическое хеширование не позволяет с абсолютной точностью определять ближайшего соседа для пробных векторов, попадающих в окрестности границ, разделяющих заданную область пространства на соответствующие кластера многомерных векторов. Поэтому для классического алгоритма геометрического хеширования необходимо осуществить ряд модификаций. При этом далее для конкретизации всех примеров будет рассматриваться такая хорошо известная база изображений лиц, как LFW. Далее будут изложены этапы, необходимые как для подготовки базы лиц, так и для самого хеширования и ускоренного поиска по базе дескрипторов.

1-й этап – фильтрация. Для каждой i-ой персоны в базе по всем дескрипторам, отвечающим различным j изображениям её лица, осуществляется поиск наиболее репрезентативного дескриптора D_i. Именно найденный наиболее репрезентативный дескриптор для каждой персоны сопоставляется ей в качестве единственного векторного идентификатора. В итоге, количество дескрипторов в дескрипторной базе будет соответствовать количеству персон в базе изображений лиц, которая может содержать в разы больше изображений по отношению к количеству персон (на одну персону, естественно, может приходится более одного изображения её лица).

2-й этап – статистические оценки. Вычисляется ряд вспомогательных величин:

В выражении (1) для определения моды гауссианы используется медианная оценка вместо средней для уменьшения влияния на неё статистических выбросов.

3-й этап – промежуточное хеширование. С учетом гауссовского распределения признаков по каждой из компонент множества векторов лицевых признаков для каждой компоненты каждого дескриптора осуществляется квантизация значений этих компонент с помощью функции erf таким образом, чтобы каждому целочисленному значению отвечало статистически одинаковое количество изображений лиц рассматриваемой базы. В частности, каждому дескриптору (хеш-ключу) D_i сопоставляется соответствующий вектор (промежуточный хеш-код) P_i (см. ниже равенства (4) и (5)).

Для определения оптимальной разрядности компонент промежуточного хеш-кода (количества разбиений/ячеек/бинов) Q (q = 0, …, Q) исходим из следующих соображений. Пусть у нас имеется пробный вектор и далее мы хотим, по крайней мере, локально для текущей компоненты абсолютно точно находить ближайшего соседа в рамках проективного приближения. Для этого кроме перебора всех дескрипторов с такой же компонентой хеш-кода q₀ необходимо сравнить и все дескриптора из соседних ячеек (q₀ ± 1), чтобы исключить проблему приграничных областей. К примеру, при разбиении на 3 ячейки в 1 из 3 случаев придется перебрать все имеющиеся в наличии дескриптора и выигрыш при индексном поиске по хеш-кодам будет незначительный в сравнении с полным перебором. Чтобы получить заметный выигрыш в индексном поиске необходимо разбить область на множество ячеек. И чем на большее количество ячеек разбита область, тем меньшая доля дескрипторов попадает в ячейки q₀ - 1, q₀ и q₀ + 1 по отношению ко всем дескрипторам в других ячейках. Что увеличивает среднестатистическую скорость индексного поиска по сравнению с полным перебором в (Q + 1)²/(3Q + 1) раз на одну компоненту. При рассмотрении R репрезентативных компонент дескрипторов алгоритм поиска по хеш-кодам быстрее полного перебора в (Q + 1)^2R/(3Q + 1)^R раз. Однако, из-за использования проективного приближения уменьшение размера ячеек будет приводить к снижению глобальной точности поиска тем сильнее, чем большее количество компонент дескрипторов задействовано в хешировании (с ростом R резко возрастает вероятность нахождения дескриптора с максимальной косинусной похожестью на сличаемый дескриптор вне выборки для поиска). Таким образом, оптимальными разбиениями являются такие, для которых Q принимает значения от 4 до 7. Далее будет рассмотрено именно сбалансированное разбиение при Q =4 (исключая собственную ячейку число проверяемых ячеек в большинстве случаев равно числу непроверяемых), обеспечивающее максимальную глобальную точность алгоритма.

Итак, P_n,i для D_n,i задается через

следующим образом:

Как упоминалось ранее, числовые значения отрезка и интервалов получаются инверсией функции erf так, чтобы в них попадало в среднем одинаковое количество дескрипторов по значениям их компонент. Для увеличения устойчивости к статистическим выбросам разбиение на интервалы делается не по среднеквадратическому отклонению значения компоненты дескриптора от моды нормального распределения текущей компоненты по всем дескрипторам, а по среднему отклонению компоненты дескриптора от этой моды (см. равенство (4)).

4-й этап – определение ключевых компонент дескрипторов и их иерархии. Далее для определения дескрипторных хеш-кодов, представляющих собой упорядоченную выборку компонент промежуточных хеш-кодов по ключевым дескрипторным компонентам, осуществляется попарное сравнение всего имеющегося множества изображений лиц по косинусной похожести C_s отвечающих им дескрипторов (соответствует скалярному произведению для дескрипторов, нормированных на единицу). Делается это следующим образом. Вначале выбирается некий уровень отсечения для косинусной похожести C_th, к примеру, равный 0.5. Затем по всей базе изображений лиц подсчитывается количество пар дескрипторов D_i и D_i', для которых косинусное сходство равно или больше рассматриваемого уровня (D_iD_i' ≥ C_th). Одновременно для каждой дескрипторной компоненты вычисляется доля e_n от выбранных пар дескрипторов, для которых ещё и значения промежуточных хеш-кодов отличаются не более чем на единицу (|P_n,i – P_n,i' | ≤ 1), то есть, принадлежат одной локальной хеш-окрестности. Далее по всем дескрипторным компонентам проверяется условие равенства единице (существует ли такое n, что e_n = 1?). Если условие не выполнилось ни для одной дескрипторной компоненты, то делается инкремент величины C_th, например на 0.05, и снова осуществляется проверка. И так до тех пор, пока не найдется одна дескрипторная компонента, для которой e_n = 1. Если же при следующем инкременте условие равенства единице выполняется сразу для нескольких e_n, то относительно предыдущего шага инкремент уменьшается, например вдвое, и по аналогии с методом бисекции находится такой уровень C_th⁽¹⁾, для которого единственная дескрипторная компонента равна единице, но не обязательно точно по условию скачка e_n в единицу. Если же за разумное количество итераций не удается разбить текущий интервал так, чтобы на интервале от C_th⁽¹⁾ до C_th⁽²⁾ для единственной компоненты выполнялось условие e_n = 1, например, из-за недостаточности разнообразия изображений лиц в базе, приводящей к существенной дискретности ряда рассчитываемых параметров, скачек в единицу происходит в одной и той же точке C_th для двух компонент e_n, то полагается C_th⁽²⁾ = C_th⁽³⁾ =… с произвольной иерархией по соответствующим n. Далее с учетом всех предыдущих шагов по C_th, которые уже могли привести к выполнению условия равенства единице для нескольких e_n, находим все интересующие нас уровни C_th^(r) (r = 1, 2, …, R), отвечающие следующему утверждению: в базе изображений лиц все лица с косинусной похожестью их дескрипторов больше или равно C_th^(r) имеют r дескрипторных компонент, для которых соответствующие компоненты их хеш-кодов принадлежат одним и тем же локальным хеш-окрестностям, и – наоборот. Тогда соответствующее упорядоченное по C_th^(r) подмножество ключевых компонент промежуточных дескрипторных хеш-кодов и формирует для каждого дескриптора его хеш-код.

На примере базы лиц LFW было получено следующее упорядоченное множество по дескрипторным компонентам:

5-й этап – получение дескрипторных хеш-кодов. Правила вычисления для всякого дескриптора D значений ряда параметров по формулам (4) и (5) наряду с использованием полученного в виде таблицы фильтра компонент и представляет собой не что иное, как определение хеш-функции, с помощью которой из дескриптора–хеш-ключа можно получать соответствующий ему семиразрядный пятиричный хеш-код H (в общем случае как числовая разрядность хеш-кода, так и его система счисления может быть иной).

6-й этап – каталогизация базы изображений лиц с соответствующими им дескрипторами по дескрипторным хеш-кодам. Для ускорения доступа в базе к объектам поиска по хеш-коду целесообразно эти объекты должным образом каталогизировать. В частности, для рассматриваемого примера базы (корневого каталога) дерево вложенных каталогов имеет вид, как показано на рисунке ниже.

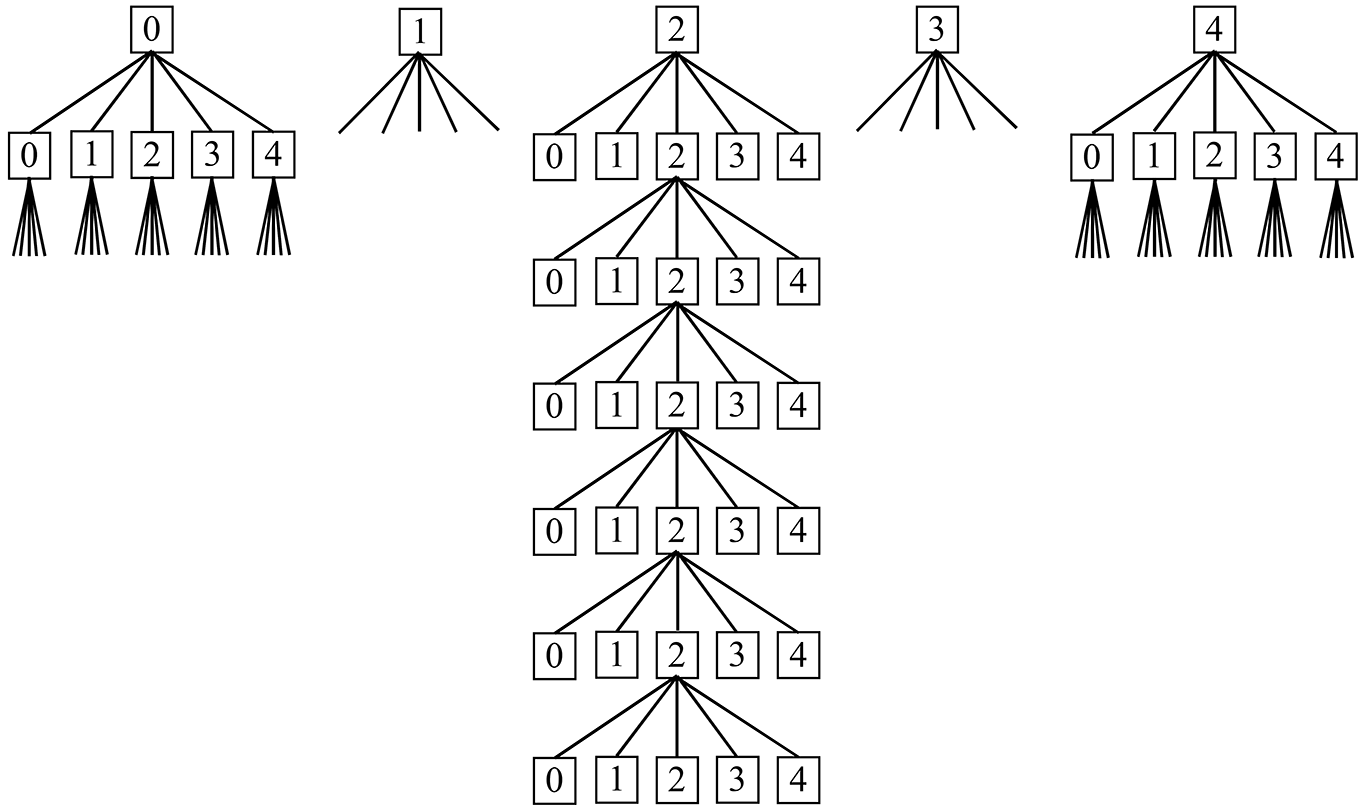
В таком случае корневой каталог содержит 5⁷ = 78125 вложенных каталогов седьмого глубочайшего уровня. Для репрезентативности каталогизированной базы изображений лиц необходимо, чтобы каждый такой вложенный каталог содержал достаточное количество файлов для разных персон. Статистически это условие более-менее обеспечивается, когда в базе содержатся изображения хотя бы для 10⁶ человек. Однако, чтобы с высокой достоверностью исключить наличие пустых каталогов на самом глубоком уровне, объем базы должен содержать информацию о 10⁷ или более различных персон. К величине аналогичного порядка можно прийти и с другой точки зрения. Современная вычислительная техника дает возможность решать рассматриваемую задачу простым полным перебором за приемлемое время даже на уровне персональных компьютеров при количестве 1–2-хкилобайтных дескрипторов в базе порядка 10⁵. Дополнительные возможности открываются с использованием многопроцессорных рабочих станций с установленными в них несколькими графическими ускорителями. С их помощью можно в рамках аналогичных временных интервалов обрабатывать полным перебором базы уже с объемами порядка 10⁶ персон. Переход к базам с объемами порядка 10⁷ персон потребует достаточно дорогостоящих решений на основе рабочих станций, объединенных в вычислительный кластер. В то же время, можно использовать предложенный метод хеширования для ускорения поиска в среднем в (25/13)⁷ » 100 раз (Q = 4) и обрабатывать с приемлемыми временными затратами на поиск по хеш-коду базы объемами около 10⁷ персон даже на персональных компьютерах. При этом базы такого объема обеспечивают отсутствие необходимости их переиндексации вследствие добавления в них новых элементов, имеющих в рамках предложенного подхода ничтожный статистический вес. Переиндексацию таких баз целесообразно проводить по счетчику новых элементов, когда их общее количество станет соизмеримым с количеством первичных элементов в базах.

Результаты

Рассмотрим теперь непосредственно сам алгоритм поиска наиболее схожего изображения лица из базы лиц на изображение лица сличаемой персоны по косинусной похожести отвечающих этим изображениям дескрипторов. Итак, пусть имеется подготовленная согласно описанному выше алгоритму база изображений лиц и соответствующих им дескрипторов, обладающая достаточной статистической репрезентативностью (>> 10⁵ персон). Предположим, что сформирован запрос на поиск для некого изображения лица по отвечающему ему дескриптору. И пусть, для определенности, это будет дескриптор, для которого с помощью вышеописанной процедуры (хеш-функции) для него получается следующий хеш-код: 0442103. Далее для всех дескрипторных коллизий хеш-кода по локальным окрестностям его компонент, в частности, при

осуществляется полный перебор отфильтрованных дескрипторов из базы (приблизительно 0.006 от их общего количества) по максимуму косинусной похожести дескрипторов. Если результатом поиска является дескриптор с косинусной похожестью не менее C_th⁽⁷⁾ (в общем случае может быть запрос на поиск нескольких наиболее похожих дескрипторов), то поиск считается удачным и заканчивается. Иначе поиск продолжается с расширением локальных хеш-окрестностей слева и справа вплоть до полного перебора на текущем уровне r с последующим переходом к следующему уровню r (от больших значений r к меньшим) пока либо найденное текущее максимальное значение косинусной похожести не сравняется или превысит C_th^(r), либо не будет осуществлен полный перебор всех дескрипторов в базе. Например, пусть для рассмотренных коллизий максимальная косинусная похожесть C_max составляет 0.52. Тогда поиск необходимо дополнительно проводить и по коллизиям

и, пусть, с тем же результатом C_max = 0.52. И так несколько раз подряд, то есть, по соответствующим нижеперечисленным коллизиям.

А по коллизиям

пусть был найден дескриптор, для которого C_max = 0.586 > C_th⁽²⁾. Полученный результат фиксируется, а поиск останавливается.

Теперь возникает резонный вопрос, а насколько часто реализуются случаи, когда при первичном поиске C_max < C_th⁽⁷⁾. Ведь в таком случае скорость поиска может снижаться в разы вплоть до полного перебора. И если такие случаи будут частыми, то существенного выигрыша от индексного поиска по хеш-коду не будет. Однако, из практики использования нейросетевых технологий вроде ArcFace наблюдения следующие. Для конкретной полученной нами реализации нейросети в достаточно редких случаях дескриптора, соответствующие весьма качественным изображениям неких персон, могут иметь косинусную похожесть на наиболее репрезентативные дескриптора этих персон менее 0.57. В то же время, в каких-то крайне редких случаях дескриптора, отвечающие изображениям лиц каких-то персон, имеют косинусную похожесть на наиболее репрезентативные дескриптора каких-то других персон более 0.61. Все эти наблюдения позволяют, в том числе, сформулировать следующую гипотезу:

– если в результате первичного поиска C_max < C_th⁽⁷⁾, то с высокой вероятностью в базе отсутствуют изображения лица сличаемой персоны.

Сам же эффект перекрытия дескрипторных кластеров для разных персон не обладает такой статистической значимостью, чтобы привести к практически полной редукции ускорения поиска по хеш-коду.