Электронная амеба и задача коммивояжера

Какой самый ценный ресурс на планете? Нефть, вода или может чистый воздух? Самый ценный ресурс, по мнению многих, это время. Его всегда не хватает, люди постоянно куда-то спешат, а любая деятельность так или иначе связана с временем: сколько баррелей нефти добывает одна нефтяная платформа в единицу времени, сколько клиентов обслуживает ресторан в единицу времени, сколько строк кода пишет программист в единицу времени и т.д. Правильное распределение задач по времени играет важную роль не только в промышленных или корпоративных масштабах, но и в быту. Мы всегда стараемся распределить свой день так, чтобы он прошел максимально эффективно и без лишних проблем. Можно сказать, что мы каждый день, сами того не подозревая, решаем свою собственную версию задачи коммивояжера. Ученые из университета Хоккайдо, вдохновившись одноклеточными амебами, решили создать аналоговый компьютер по их подобию, который может предложить самый эффективный метод решения знаменитой задачи комбинаторной оптимизации. Почему именно амебы стали вдохновителями этого труда, по какому принципу работала созданная система, и насколько эффективно она решала задачу коммивояжера? Об этом мы узнаем из доклада ученых. Поехали.

Основа исследования

Основная цель комбинаторной оптимизации заключается в поиске не только самого решения задачи, но и в поиске оптимального метода его достижения. Задачи, требующие применения оптимизации, встречаются повсеместно: от распределения рейсов самолетов до поиска такси. Подавляющее большинство обычных компьютеров не способны решать сложные задачи по оптимизации, так как с увеличением сложности задачи растет и число возможных вариантов ее решения, причем экспоненциально.

Задача коммивояжера (или TSP от travelling salesman problem) является одним из ярчайших примеров комбинаторной оптимизации.

По своей сути TSP звучит довольно просто: определить самый оптимальный (самый короткий, самый быстрый и т.д.) маршрут, проходящий через указанные города с возвращением в исходный. Но вот решений у этой задачи, как и методов их достижения, несколько.


Симметричная задача коммивояжера.

Самый очевидный метод решения это подсчитать длины всех возможных маршрутов и выбрать самый короткий. Однако этот метод очень быстро сталкивается с большой проблемой: например, для симметричной задачи коммивояжера с n городами существует (n-1)!/2 возможных маршрутов, т.е. для 15 городов существует 43 миллиарда возможных маршрутов. Вполне очевидно, что пересчитывать все их, хоть вручную, хоть с помощью алгоритма, это длительный и трудоемкий процесс.

Существуют также и алгоритмы, основанные на природных процессах, которые сформулированы для параллельного обновления нескольких переменных для достижения быстрого поиска решения задачи. Чего не скажешь про последовательные процессы в ЦПУ, который управляет одним битом за раз, а потому может имитировать параллелизм в очень ограниченном виде. Следовательно, есть необходимость разработки архитектуры, которая смогла бы реализовать подобные природные алгоритмы.

Одной из первых физических вычислительных систем для решения задачи TSP была рекуррентная нейронная сеть Хопфилда, реализованная с помощью электронной цепи. Однако система была не так идеальна, как хотелось бы, поскольку она часто сходилась в состоянии локального минимума (решение низкого качества), а порой и не могла определить подходящий маршрут для задачи TSP с определенными параметрами. Фактически, для некоторых случаев TSP с 10 городами сообщалось, что вероятность нахождения оптимального решения составляла не более 20%.

В последние годы большой популярностью пользуются квантовые вычисления. Поиск решения TSP не стал исключением. К примеру, машина Изинга, основанная на механизме квантового отжига*.

Квантовый отжиг* — метод наложения глобального минимума заданной функции среди набора решений-кандидатов.

Данная машина ищет оптимальное решение, сопоставляя проблему с процессом нахождения спина с минимальной энергией в модели Изинга*, описывающей намагничивание материала.

Модель Изинга*: к каждой вершине кристаллической решетки приписывается число (спин), равное +1 или -1. Каждому из 2^N возможных вариантов расположения спина (N – число атомов решетки) приписывается энергия, получающаяся из попарного взаимодействия спинов соседних атомов.

Проблема в том, что настройка параметров для системы на базе модели Изинга это сложный и дорогостоящий процесс. Для TSP с n городами стандартная структура спиновых переменных разреженной связностью требует введения избыточных переменных в порядке N⁴ для обработки нерегулярно распределенных городов, что приводит к быстрому увеличению площади схемы.


Изображение №1

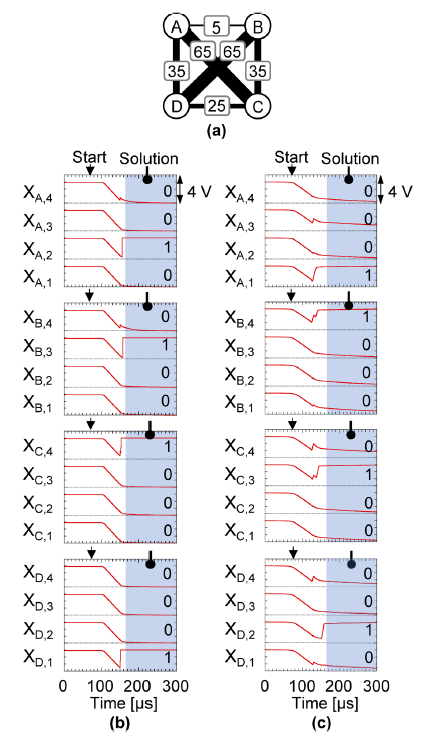
На 1а показана графическая структура модели Изинга, которая называется химерным графом. В такой структуре согласованность между избыточными переменными потенциально может быть нарушена. Когда настройка параметров не может быть произведена должным образом, модель Изинга иногда сходится в недопустимом состоянии, в котором нарушаются ограничения TSP: повторное посещение однажды посещенного города и одновременное посещение нескольких городов.

Вполне ожидаемо, что авторы рассматриваемого нами сегодня труда не захотели использовать машину Изигна в качестве вдохновения. Вместо этого они обратились к самому популярному вдохновителю — к природе.

Созданная система была названа «электронной амебой», поскольку была основана на поведении одноклеточного амебоидного организма (Physarum polycephalum), ищущего пищу и избегающего опасностей.

В электронной амебе произвольная TSP задача может быть отображена на цепи резисторов перекрестной структуры (1b) которая была названа «схемой отображения задач» (или IMC от instance-mapping circuit).

Архитектура IMC аналогична архитектуре рекуррентной нейронной сети Хопфилда, о которой упоминалось ранее. Однако она связана с ядром амебы (2а), что помогает избежать конвергенции в неверном состоянии (неверном решении задачи, т.е. несоответствующем ограничениям задачи).


Изображение №2

Ученые отмечают, что ранее уже работали над электронной амебой, но исключительно в теоретическом формате. В данном же исследовании благодаря численному моделированию и лабораторным экспериментам с использованием физически созданных цепей (2b) им удалось доказать на практике, что электронная амеба находит самое эффективное решение TSP задачи за время, которое пропорционально N.

Результаты исследования

На изображении 2а показана схема электронной амебы, состоящая из ядра амебы и IMC, которая электронно имитирует динамику поиска решения так называемого компьютера на основе амебы, который использует живую амебу для поиска решения TSP. Состояние каждого блока в ядре амебы представляет решение о том, где и когда посетить определенный город.

IMC реализует тип управления с обратной связью, называемый контролем возврата, который относится к ограничениям TSP и расстояниям между городами в соответствии с заданной картой и отправляет сигнал возврата каждому блоку в ядре амебы.

Сначала на обычном компьютере проводилось численное моделирование с использованием имитатора цепи, которое должно было показать, сможет ли электронная амеба решить TSP задачу с 4 городами (3а).


Изображение №3

На изображении 3b показан пример формы выходного сигнала, полученного в результате моделирования схемы. Индексы состояния X_{V, k} каждого объекта, т.е. V и k означают, что город V посещается k-тым в очереди.

Первоначально каждый блок принимает состояние 1, потому что заряд конденсатора установлен на ноль. Затем IMC отправляет сигналы возврата ко всем устройствам, чтобы изменить их состояние с 1 на 0, так как состояния, где все единицы (т.е. 1), нарушают ограничения TSP. Состояние каждого блока постепенно приближается к 0 при зарядке конденсатора путем подачи тока от источника. После того как несколько возвратов были вызваны контроллером, динамика всех блоков становится стабильной (заштрихованная область на 3b).

В этот момент электронная амеба находит оптимальное решение D → A → B → C → D, которое соответствует кратчайшему пути.

Посредством имитатора цепи была проверена способность электронной амебы решать задачи с числом N от 10 до 30 городов. Для каждого варианта N менее 20 было выполнено по 50 испытаний, а для N более 20 городов — по одному испытанию. Поскольку время моделирования крайне быстро возрастало, для задач с 20 городами требовалось 5 часов, для задач с 30 городами — уже 6 дней.

В каждом испытании сопротивление было случайным образом назначено от 1 Ом до 10 кОм, чтобы электронная амеба исследовала более широкое пространство состояний.

Всего было проведено 560 испытаний, и в каждом из них вероятность нахождения верного решения составляла 100%. Объясняется это тем, что ядро ​​амебы всегда стабилизировалось в устойчивое состояние, в котором никакая переменная не нарушает ограничения TSP задачи. В таком состоянии никакие дальнейшие изменения во всех блоках ядра амебы не индуцируются обратными сигналами.


Изображение №4

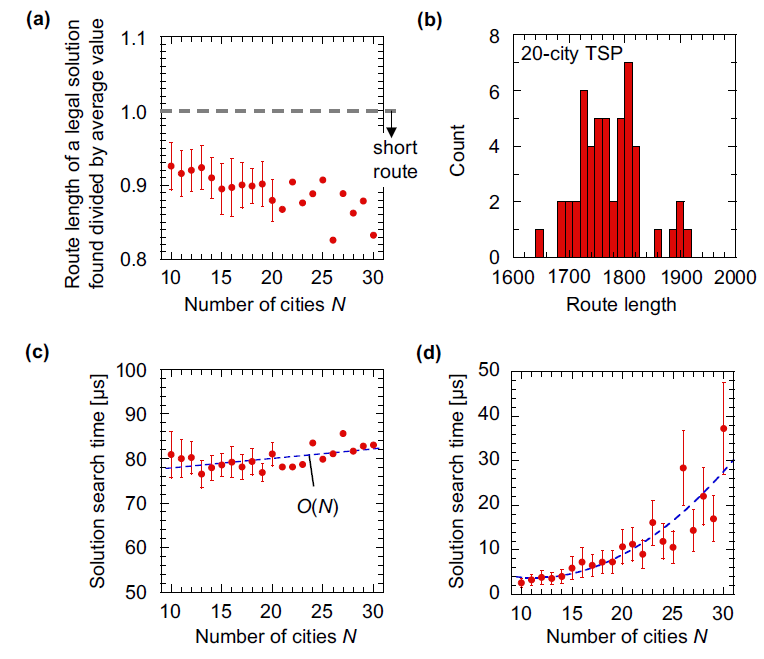
На 4а показана длина маршрута, полученная симулятором цепи. Тут вертикальная ось нормирована на среднюю длину маршрута, полученную в результате случайной выборки из 10 000 испытаний. Если значение на вертикальной оси меньше 1.0, это означает, что точность найденного решения выше, чем точность, найденная при случайной выборке. Другими словами, электронная амеба находит более верные решения, чем случайная выборка. Кроме того, точность работы системы не уменьшалась, даже когда число городов было увеличено.

Путем внесения случайных изменений в значение сопротивления блока каждый из них менял скорость перехода из состояния 1 в 0, в результате чего было найдено множество верных решений (4b). Система могла показать сразу несколько верных решений для одной и той же задачи, однако не могла гарантировать достижение оптимального маршрута.

На 4с показано, что среднее время, необходимое электронной амебе для поиска верного решения, увеличивается почти линейно как функция N.

Численное моделирование, названной «AmoebaTSP», показало, что линейное решение может быть достигнуто, если центр одноклеточного организма может поставлять внутриклеточные ресурсы для роста его ветвей с постоянной скоростью, даже при ответе на сигналы отскока. Работа в линейном режиме приписывается конструкции механизма управления отскоком вместе с параллельными операциями всех блоков в ядре амебы.

Блоки пытаются выбрать более короткий путь между двумя городами в соответствии с информацией о длинах возможных путей посредством накопления и сравнения опыта подавления сигналов возврата. Правило возврата построено таким образом, что после того, как путь и порядок посещения городов определены, ядру амебы запрещено изменять решение. Таким образом, система определяет каждый путь один за другим, избегая неверных (т.е. не соответствующих ограничениям задачи) путей. При этом время поиска правильного пути может быть сокращено за счет увеличения тока и/или уменьшения емкости.

Далее ученые провели сравнение эффективности работы своей системы (электронной амебы) и классического стохастического алгоритма локального поиска 2-opt, который не требует оптимизации параметров.

Качество решения, полученного с помощью 2-opt, становится выше (и в конечном итоге достигает насыщения) по мере того, как его основная операция повторяется большее количество раз. Однако процесс был прерван, когда качество стало равным качеству, полученному с помощью электронной амебы. Таким образом можно было сравнить показатель времени, необходимого для завершения задачи.

Как показано на 4d, время, которое потребовалось 2-opt для решения задачи, увеличивалось квадратично в соответствии со сложностью задачи. В случае электронной амебы наблюдалось линейное увеличение времени, необходимого для решения такой же задачи (4с).

Из этого следует, что электронная амеба может куда эффективнее справляться с задачами за более короткое время, чем классический алгоритм 2-opt. При этом для выполнения данного процесса подойдет обычный компьютер.

Изготовленная с помощью КМОП-устройств электронная амеба (2b) показала отличные результаты в решении задачи с четырьмя городами (5а-5е).


Изображение №5


Таблица №1: данные по TSP и длинам маршрутов.

Поскольку ядро амебы состоит из 16 ветвей, есть возможность создать маршрут для произвольных задач с четырьмя городами, меняя значение сопротивления в IMC.

Графики на 5а-5е показывают, что система нашла кратчайший маршрут для экземпляров A–C и E, где было выполнено 50 испытаний для каждого варианта задачи без изменения значений сопротивления.

Любопытно, что для задачи D система не смогла определить кратчайший маршрут (5d), хотя длина самого короткого маршрута для D равна оной для С. Это может быть связано с рядом неточностей в изготовленной схеме, таких как вариативность порогового напряжения в КМОП инверторе, вариативность напряжения смещения в операционном усилителе и разница в длине проводки в IMC, что может создать предпочтение при выполнении решение. Однако, когда длины маршрутов широко распределены (например, для варианта E), система достигала оптимального решения, преодолевая предпочтение.

Ученые отмечают, что машинам Изинга необходимо затратить значительные усилия на процессы отображения проблем и настройки параметров до поиска решения. Если эта предварительная обработка будет выполнена должным образом, то производительность модели Изинга в сочетании с имитацией квантового отжига будет гораздо выше, чем у электронной амебы, в противном случае она не сможет достичь даже верного решения (соответствующего ограничениям задачи).

Напротив, электронной амебе нет необходимости выполнять сложную предварительную обработку, так как IMC предлагает высокую гибкость отображения проблем с его неограниченной связью между произвольной парой переменных и требует только простых числовых операций для определения параметров.

Более того, если резисторы в IMC заменить на мемристоры или атомарные переключатели, что позволяет перезаписывать динамическое сопротивление, TSP задачи можно обновлять прямо посреди процесса поиска решения. Такой динамически перезаписываемый IMC позволит электронной амебе устойчиво реагировать на внезапные изменения ограничений задачи, вызванные неожиданными отказами, возникающими в постоянно меняющихся практических ситуациях.

Еще одним важным аспектом данной разработки является ее масштабируемость, говорят ученые. Для решения TSP задачи с N городами ядру амебы требуется N² блоков, а для поперечного IMC — 2N² проводов и N⁴ резисторов в точках пересечения проводов. Таким образом, площадь схемы электронной амебы увеличивается примерно на N², что значительно меньше и дешевле, чем у машин Изинга, которым требуется площадь порядка N⁴.

Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых и дополнительные материалы к нему.

Эпилог

В данном труде ученые показали, что для решения произвольной задачи коммивояжера может быть использована разработанная ими электронная амеба. Данное устройство было вдохновлено одноклеточным организмом и его поведением в процессе поиска пищи и избегания опасности. Электронная амеба позволяет за счет простых операций определения сопротивления в IMC быстро начать процесс поиска решения задачи без необходимости в долгих приготовлениях, как это происходит в случае машин Изинга. Сам же процесс поиска решения протекает линейно за счет спонтанной динамики электрического тока в ядре амебы.

Ученые заявляют, что их разработка отлично подходит для приложений, где скорость решения задачи куда важнее качества. К примеру, в случае природного катаклизма либо техногенной катастрофы, когда необходимо предоставить надежные маршруты эвакуации, быстрое решение часто является куда более важным, чем поиск самого оптимального маршрута.

Кроме того электронная амеба может быть использована в случае, когда число городов в задаче превышает сотню. В таком варианте она намного производительнее, чем классический алгоритм стохастического локального поиска. Не менее важен и факт того, что электронная амеба является довольно компактным устройством, габариты которого можно будет в дальнейшем уменьшить.

В будущем ученые намерены продолжить свою работу, сконцентрировавшись на повышении качества найденных амебой решений.

Данный труд показывает не только то, что природа продолжает вдохновлять ученых на самые невероятные исследования, но и то, что аналоговые компьютеры, состоящие из простых и компактных схем, чем по сути и является электронная амеба, отлично подходят для решения реальных задач.

Благодарю за внимание, оставайтесь любопытствующими и хорошей всем рабочей недели, ребята. :)

Немного рекламы

Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).

Dell R730xd в 2 раза дешевле в дата-центре Equinix Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?