F-тест качества спецификации множественной регрессионной модели

Здравствуй, Хабр!

Цель этой статьи — рассказать о роли степеней свободы в статистическом анализе, вывести формулу F-теста для отбора модели при множественной регрессии.

1. Роль степеней свободы (degree of freedom) в статистике

Имея выборочную совокупность, мы можем лишь оценивать числовые характеристики совокупности, параметры выбранной модели. Так не имеет смысла говорить о среднеквадратическом отклонении при наличии лишь одного наблюдения. Представим линейную регрессионную модель в виде:

$y_{i}\text{=}\,\beta_{0}\text{+}\beta_{1}\text{x}\,\text{+}\,\varepsilon_{i} (1)$

Сколько нужно наблюдений, чтобы построить линейную регрессионную модель? В случае двух наблюдений можем получить идеальную модель (рис.1), однако есть в этом недостаток. Причина в том, что сумма квадратов ошибки (MSE) равна нулю и не можем оценить оценить неопределенность коэффициентов $\beta_0,\beta_1$ . Например не можем построить доверительный интервал для коэффициента наклона по формуле:

$\beta_{1}\pm t_{\left(\frac{\alpha}{2},\,n-2\right)}\cdot\frac{{\sqrt[]{MSE}}\text{}}{\sum\limits_{i=1}^{n}\left(x_{i}-\overline{x}\right)^{2}}\,\, (2)$

А значит не можем сказать ничего о целесообразности использования коэффициента $\beta_1$ в данной регрессионной модели. Необходимо по крайней мере 3 точки. А что же, если все три точки могут поместиться на одну линию? Такое может быть. Но при большом количестве наблюдений маловероятна идеальная линейная зависимость между зависимой и независимыми переменными (рис. 1).

Количество степеней свободы - количество значений, используемых при расчете статистической характеристики, которые могут свободно изменяться. С помощью количества степеней свободы оцениваются коэффициенты модели и стандартные ошибки. Так, если имеется n наблюдений и нужно вычислить дисперсию выборки, то имеем n-1 степеней свободы.

$s^{2}=\frac{\sum_{i=1}^{n}\left(y_{i}- \overline{y}\right)^{2}}{df}=\frac{\sum_{i=1}^{n}\left(y_{i}- \overline{y}\right)^{2}}{n-1} (3)$

Мы не знаем среднее генеральной совокупности, поэтому оцениваем его средним значением по выборке. Это стоит нам одну степень свободы.

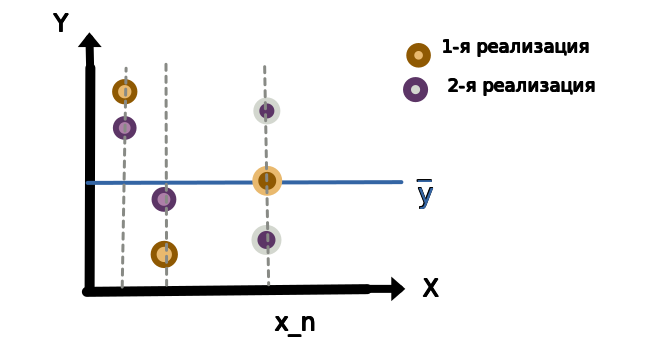
Пусть известны сумма квадратов отклонений $\nu$ , среднее значение $\hat y$ . Возьмем несколько реализаций значений $y_{i},i=\,\overline{1,n-1}$ . Тогда для выполнения равенства

$\sum_{i=1}^{n}\left(y_{i}- \overline{y}\right)^{2}=\nu$ значение y_n должно быть фиксированное.

Пример представлен на рисунке 2.

Рисунок 2 - пояснение к степеням свободы

Представим теперь что имеется 4 выборочных совокупностей (рис.3).

Каждая выборочная совокупность имеет свое среднее значение, определяемое по формуле $\mu_{Y}=\beta_{0}+\beta_{1}x$ . И каждое выборочное среднее может быть оценено $\hat{y}_{i}=\,b_{0}\,+\,b_{1}x_{i}$ . Для оценки мы используем 2 параметра $\beta_0, \beta_1$ , а значит теряем 2 степени свободы (нужно знать 2 точки). То есть количество степеней свобод $df\,=\,n\,-\,2$ Заметим, что при 2 наблюдениях получаем 0 степеней свободы, а значит не можем оценить коэффициенты модели и стандартные ошибки.

Таким образом сумма квадратов ошибок имеет (SSE, SSE - standard error of estimate) вид:

$SSE=MSE=\frac{\sum_{i=1}^{n}\left(y_{i\,}-\hat{y}_{i}\right)^{2}}{n-2} (4)$

Стоит упомянуть, что в знаменателе стоит n-2, а не n-1 в связи с тем, что среднее значение оценивается по формуле $\hat{y}_{i}=\,b_{0}\,+\,b_{1}x_{i}$ . Квадратные корень формулы (4) - ошибка стандартного отклонения.

В общем случае количество степеней свободы для линейной регрессии рассчитывается по формуле:

$df\,=\,n\,-\,k\,-\,1, (5)$

где n - число наблюдений, k - число независимых переменных.

2. Анализ дисперсии, F-тест

При выполнении основных предположений линейной регрессии имеет место формула:

$\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}=\sum_{i=1}^{n}\left(\hat{y_{i}}-\,\bar{y}\right)^{2}\,+\,\sum_{i=1}^{n}\left(y_{i}-\,\hat{y_{i}}\right)^{2}\ , (6)$

где $\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}\,\text{-}\;\text{SSTO}\;\text{(Total}\;\text{sum}\;\text{of}\;\text{squares)}$ ,

$\sum_{i=1}^{n}\left(\hat{y_{i}}-\bar{y}\right)^{2}\,\text{-}\;\text{SSR}\;\text{(Regression}\;\text{Sum}\;\text{of}\;\text{squares)}$ ,

$\sum_{i=1}^{n}\left(y_{i}-\hat{y_{i}}\right)^{2}\,\text{-}\;\text{SSE}\;\text{(Error}\;\text{sum}\;\text{of}\;\text{squares)}$

В случае, если имеем модель по формуле (1), то из предыдущего раздела знаем, что количество степеней свободы у SSTO равно n-1. Количество степеней свободы у SSE равно n-2. Таким образом количество степеней свободы у SSR равно 1. Только в таком случае получаем равенство $\left(n-1\right)\,=\,\left(1\right)\,+\,\left(n-2\right)$ .

Масштабируем SSE и SSR с учетом их степеней свободы:

$MSE\,=\,\frac{\sum_{i=1}^{n}\left(y_{i}-\hat{y_{i}}\right)^{2}}{n-2}=\frac{SSE}{n-2} (7)$ $MSR\,=\,\frac{\sum_{i=1}^{n}\left(\bar{y_{i}}-\hat{y_{i}}\right)^{2}}{1}=\frac{SSR}{1} (8)$

Получены хи-квадрат распределения. F-статистика вычисляется по формуле:

$F\,=\frac{MSR}{MSE} (9)$

Формула (9) используется при проверке нулевой гипотезы $H_{0}:\beta_{1}=0$ при альтернативной гипотезе $H_{1}:\beta_{1}\neq0$ в случае линейной регрессионной модели вида (1).

3. Выбор линейной регрессионной модели

Известно, что с увеличением количества предикторов (независимых переменных в регрессионной модели) исправленный коэффициент детерминации увеличивается. Однако с ростом количества используемых предикторов растет стоимость модели (под стоимостью подразумевается количество данных которые нужно собрать). Однако возникает вопрос: “Какие предикторы разумно использовать в регрессионной модели?”. Критерий Фишера или по-другому F-тест позволяет ответить на данный вопрос.

Шаги:

Определим “полную” модель: $y_{i}^{F}=\left(\beta_{0}+\beta_{1}x_{i1}+...+\beta_{k}x_{ik}\right)\,+\,\varepsilon_{i}$ (10)
Определим “укороченную” модель: $y_{i}^{R}=\left(\alpha_{0}+\alpha_{1}x_{i1}+...+\alpha_{t}x_{it}\right)\,+\,\varepsilon_{i}$ (11)
Вычисляем сумму квадратов ошибок для каждой модели:
$\text{SSE(F)}\;=\,\sum_{i=1}^{n}\left(y_{i}-\widehat{y_{i}^{F}}\right)^{2}$ (12)
$\text{SSE(R)}\;=\,\sum_{i=1}^{n}\left(y_{i}-\widehat{y_{i}^{R}}\right)^{2}$ (13)
Определяем количество степеней свобод $df_{F},\,df_{R}$
Рассчитываем F-статистику:
$F\,=\,\left(\frac{SSE\left(R\right)-SSE\left(F\right)}{df_{R}-df_{F}}\right)\,\div\,\left(\frac{SSE\left(F\right)}{df_{F}}\right)$ (14)
Нулевая гипотеза - “укороченная” модель мало отличается от “полной (удлиненной) модели”. Поэтому выбираем “укороченную” модель. Альтернативная гипотеза - “полная (удлиненная)” модель объясняет значимо большую долю дисперсии в данных по сравнению с “укороченной” моделью.

Коэффициент детерминации из формулы (6):

$R^{2}=\,\frac{SSR}{SSTO}=1-\frac{SSE}{SSTO} (15)$

Из формулы (15) выразим SSE(F):

$\text{SSE(F)}\;\text{=}\;\left(1-R^{2}\right)SSTO (16)$

SSTO одинаково как для “укороченной”, так и для “длинной” модели. Тогда (14) примет вид:

$F\,=\,\left(\frac{SSE\left(R\right)-SSE\left(F\right)}{df_{R}-df_{F}}\right)\,\div\,\left(\frac{\left(1-R_{F}^{2}\right)SSTO}{df_{F}}\right) (14a)$

Поделим числитель и знаменатель (14a) на SSTO, после чего прибавим и вычтем единицу в числителе.

$F\,=\,\left(\frac{\left(-1\,+\,\frac{SSE\left(R\right)}{SSTO}\right)+\left(1-\frac{SSE\left(F\right)}{SSTO}\right)}{df_{R}-df_{F}}\right)\,\div\,\left(\frac{\left(1-R^{2}\right)}{df_{F}}\right) (14б)$

Используя формулу (15) в конечном счете получим F-статистику, выраженную через коэффициенты детерминации.

$F\,=\,\left(\frac{R_{F}^{2}-R_{R}^{2}}{df_{R}-df_{F}}\right)\,\div\,\left(\frac{\left(1-R_{F}^{2}\right)}{df_{\,F}}\right) (14 в)$

3 Проверка значимости линейной регрессии

Данный тест очень важен в регрессионном анализе и по существу является частным случаем проверки ограничений. Рассмотрим ситуацию. У линейной регрессионной модели всего k параметров (Сейчас среди этих k параметров также учитываем $\beta_0$ ).Рассмотрим нулевую гипотеза — об одновременном равенстве нулю всех коэффициентов при предикторах регрессионной модели (то есть всего ограничений k-1). Тогда “короткая модель” имеет вид $y_{i}^{R}=\beta_{0}+\varepsilon_{i}$ . Следовательно $R_{R}^{2}=0, df_{R}=n-1, df_{F}=n-k$ . Используя формулу (14.в), получим

$F\,=\,\left(\frac{R_{F}^{2}}{k-1}\right)\,\div\,\left(\frac{\left(1-R_{F}^{2}\right)}{n-k}\right)\,\sim\,F\left(k-1,\,n-k\right)$

Заключение

Показан смысл числа степеней свободы в статистическом анализе. Выведена формула F-теста в простом случае(9). Представлены шаги выбора лучшей модели. Выведена формула F-критерия Фишера и его запись через коэффициенты детерминации.

Можно посчитать F-статистику самому, а можно передать две обученные модели функции aov, реализующей ANOVA в RStudio. Для автоматического отбора лучшего набора предикторов удобна функция step.

Надеюсь вам было интересно, спасибо за внимание.

При выводе формул очень помогли некоторые главы из курса по статистике STAT 501

Теги:

F-тест
Отбор моделей
Линейная регрессия

Хабы:

Математика
Статистика

Источник: https://habr.com/ru/post/592677/

Вернуться к списку

Интересные статьи

Способы обеспечения качества данных для машинного обучения

Данные — это душа каждой модели машинного обучения. В этой статье мы расскажем о том, почему лучшие команды мира, занимающиеся машинным обучением, тратят больше 80% своего времени на улучшение трениро...

Дюна: ученые смоделировали пустынную планету Арракис, чтобы посмотреть, смогут ли там выжить люди

Кто контролирует спайс — тот контролирует Вселенную. Недавно все (кто успел до локдауна) радовались новой экранизации легендарной «Дюны», в этот раз режиссера Дени Вильнева. Снова разгорелись споры о ...

«Вертушки» до 25 тысяч рублей — три избранные модели

Ранее мы поговорили о проигрывателях, цена на которые «плавает» в районе двадцати тысяч рублей, чуть спускается под эту планку, доходит до пятнадцати тысяч и становится еще более скромной для самых ба...

Заметки Дата Сайентиста: на что обратить внимание при выборе модели машинного обучения — персональный топ-10

Мы снова в эфире и продолжаем цикл заметок Дата Сайентиста и сегодня представляю мой абсолютно субъективный чек-лист по выбору модели машинного обучения. Это топ-10 свойств задач...

Чем полезны 3D-модели сложных производств

Нефтехимические комбинаты это весьма и весьма сложные комплексы зданий. Наш ЗапСибНефтеХим в Тобольске — крупнейший объект за всю историю современной России. 9 831 километр кабеля, 102 000 тонн м...