FermiNet: квантовая физика и химия с азов

В статье, недавно опубликованной в Physical Review Research, мы демонстрируем, как при помощи глубокого обучения упрощается решение фундаментальных квантовомеханических уравнений для реальных систем. При этом решается не только принципиальный научный вопрос, но и открываются перспективы для практического использования полученных результатов в будущем.

Исследователи смогут прототипировать новые материалы и соединения in silico прежде, чем попытаться синтезировать их в лаборатории. Также выложен код из этого исследования; таким образом, команды специалистов по вычислительной физике и химии могут опираться на проделанную работу и применять ее при решении разнообразных проблем. В рамках исследования была разработана новая архитектура нейронной сети, Fermionic Neural Network или FermiNet, которая хорошо подходит для моделирования квантового состояния больших совокупностей электронов – а ведь именно на электронах основаны все химические связи. Сеть FermiNet впервые продемонстрировала, как использовать глубокое обучение для вычисления энергии атомов и молекул с азов. Полученная модель оказалась достаточно точной для практического применения и на момент публикации оригинала статьи (октябрь 2020) оставалась наиболее точным нейросетевым методом, применяемым в отрасли. Предполагается, что связанные с ней методы и инструментарий могут пригодиться при решении фундаментальных проблем в естественных науках. Авторы FermiNet уже применяют ее в работе над сверткой белков, динамикой стеклообразных соединений, квантовой хромодинамикой на решетке и во многих других проектах, помогающих воплотить данные наработки на практике.

Краткая история квантовой механики

Упомянув «квантовую механику», вы, скорее всего, озадачите собеседника этой темой как никакой иной. Сразу вспоминаются такие образы, как кот Шрёдингера, который парадоксально может быть одновременно жив и мертв, а также элементарные частицы, которые одновременно являются и корпускулами, и волнами. В квантовой системе такая частица как электрон не имеет конкретного местоположения, в отличие от ситуации в классической физике. В квантовой физике позиция электрона описывается облаком вероятностей – то есть, размазана по всем тем точкам, в каждой из которых может оказаться электрон. Из-за такого абсурдного состояния вещей Ричард Фейнман счел возможным заявить: «Думаю, я смело могу сказать, что квантовой механики никто не понимает».

Несмотря на всю эту жутковатую странность, суть теории можно выразить всего в нескольких стройных уравнениях. Наиболее знаменитое из них, уравнение Шрёдингера, описывает поведение частиц в квантовых масштабах тем же образом, каким уравнения Ньютона описывают поведение тел в более привычных нам макроскопических масштабах. Тогда как интерпретация этого уравнения любого заставит схватиться за голову, математическая его составляющая гораздо проще для практического использования, благодаря чему и родилось известное профессорское «заткнись и считай», которым они отбивались от неудобных философских вопросов, прилетающих от студентов.

Эти уравнения достаточны, чтобы описать поведение всей привычной нам материи на уровне атомов и ядер. Нелогичная составляющая квантовой механики лежит в основе всевозможных экзотических феноменов: сверхпроводимость, сверхтекучесть, лазер и полупроводники возможны только благодаря квантовым эффектам. Но даже такая скромная штука как ковалентная связь – базовая составляющая всей химии – является результатом квантовых взаимодействий электронов. Когда эти правила были окончательно проработаны в 1920-е, ученые осознали, что впервые создана теория, детально описывающая работу всей химии. В принципе, квантовые уравнения можно было бы просто адаптировать для различных молекул, решать их с учетом энергии системы, а затем определять, какие молекулы будут стабильны, и какие реакции будут происходить спонтанно. Но, когда была предпринята попытка сесть и вычислить решения для этих уравнений, выяснилось, что это осуществимо для простейшего атома (водорода) и практически ни для одного другого. Все остальные расчеты оказались слишком сложны.

Головокружительный оптимизм тех дней красиво сформулировал Поль Дирак:

Итак, базовые физические законы, необходимые для математической теории, которая бы описывала большую часть физики и всю химию, уже известны. Загвоздка в том, что на практике применение этих законов дает слишком сложные уравнения, решить которые нам объективно не под силу. Поэтому представляется желательным разработать приблизительные методы для практического применения квантовой механики.
1929

Многие подхватили призыв Дирака, и вскоре физики взялись за разработку математических методов, которые позволили бы аппроксимировать поведение молекулярных связей и другие химические явления на качественном уровне. Все началось с приблизительного описания поведения электронов – эти сведения изучаются во вводном курсе химии. При таком описании каждый электрон выводится на свою орбиталь, которая позволяет рассчитать вероятность того, что электрон будет обнаружен в конкретной точке в окрестностях атомного ядра. В таком случае форма каждой орбитали зависит от усредненной формы всех других орбиталей. Поскольку в таком описании по модели «самосогласованного поля» считается, что каждый электрон прикреплен всего к одной орбитали, эта картина очень неполно передает реальные свойства электронов. Тем не менее, ее достаточно, чтобы определить общую энергию молекулы с погрешностью всего около 0,5%.



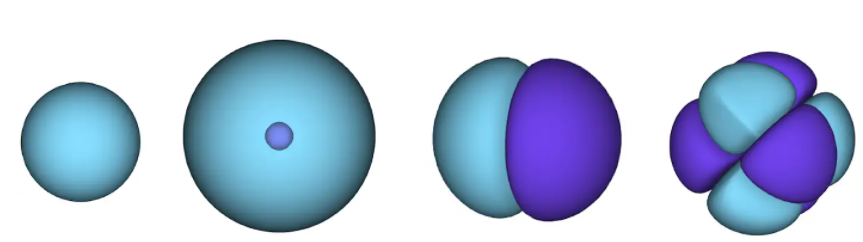
Рисунок 1 – атомные орбитали. поверхность – это область, в которой с высокой вероятностью может находиться электрон. в голубой области волновая функция положительна, а в фиолетовой – отрицательна.

К сожалению, для практикующего химика ошибка в 0,5% слишком велика, чтобы с ней можно было мириться. Энергия молекулярных связей – лишь малая толика общей энергии системы, и верный прогноз того, будет ли молекула стабильна, зачастую может зависеть всего от 0,001% общей энергии системы или примерно от 0,2% остающейся «корреляционной» энергии.

Например, тогда как общая энергия электронов в молекуле бутадиена составляет почти 100 000 килокалорий на моль, энергетическая разница между различными возможными конфигурациями молекулы составляет всего 1 килокалорию на моль. То есть, при необходимости правильно спрогнозировать естественную форму молекулы бутадиена, требуется такой же уровень точности, как при измерении ширины футбольного поля с точностью до миллиметра.

С распространением электронной вычислительной техники вскоре после Второй мировой войны, ученые разработали целую уйму вычислительных методов, которые не сводились к такому описанию по методу самосогласованного поля. Эти методы обозначаются невообразимой кучей аббревиатур, охватывающих весь алфавит, но в каждом из этих методов заключен тот или иной компромисс между точностью и эффективностью. На одном полюсе находятся методы, которые, в сущности, точны, но масштабируются хуже чем по экспоненте с увеличением количества электронов – поэтому не годятся для работы с большинством молекул, кроме самых мелких. На другом полюсе – методы, которые масштабируются линейно, но не слишком точны. Эти вычислительные методы оказали колоссальное влияние на практическую химию – Нобелевская премия по химии за 1998 год была вручена авторам многих из этих алгоритмов.

Фермионные нейронные сети

Несмотря на всю широту существующих вычислительных квантовомеханических инструментов, проблема эффективного представления информации требовала разработать новый метод. Неслучайно в крупнейшие современные квантовохимические расчеты вовлекаются лишь десятки тысяч электронов (речь о самых приблизительных методах), тогда как классические методы химических расчетов, например, молекулярная динамика, позволяют обращаться с миллионами атомов. Состояние классической системы описать не сложно – требуется всего лишь отследить положение и импульс каждой частицы. Представить состояние квантовой системы – гораздо более серьезный вызов. Приходится присвоить вероятностное значение каждой возможной конфигурации позиций электронов. Эта информация кодируется в волновой функции, позволяющей присвоить положительное или отрицательное число каждой конфигурации электронов, а волновая функция в квадрате дает вероятность, с которой система может быть найдена в такой конфигурации. Пространство всех возможных конфигураций колоссально – если бы вы попытались представить его как сетку со 100 точками по каждому измерению, то количество возможных конфигураций электронов для атома кремния было бы больше, чем количество атомов во Вселенной!

Именно в такой ситуации могут пригодиться глубокие нейронные сети. В последние несколько лет были достигнуты огромные успехи в представлении при помощи нейронных сетей сложных вероятностных распределений с высокой размерностью. Теперь известно, как эффективно обучать такие сети с расчетом на их масштабирование. Мы предположили: коль скоро эти сети уже доказали свою прыть при обучении функций с многими измерениями при решении задач из области искусственного интеллекта, может быть, они сгодятся и для представления квантовых волновых функций. Не нас первых посетили такие мысли – другие исследователи, в частности, Джузеппе Карлео и Маттиас Тройер продемонстрировали, как современное глубокое обучение применимо для решения идеализированных квантовых задач. Мы хотели воспользоваться нейронными сетями, чтобы подступиться к более реалистичным проблемам в химии и в физике твердого тела, а это означало, что нам потребуется учесть в наших расчетах электроны.

При работе с электронами есть всего один нюанс. Электроны должны подчиняться принципу запрета Паули, то есть, два электрона не могут одновременно находиться в одном и том же месте. Дело в том, что электроны – это элементарные частицы из числа фермионов, входящих в состав большинства первокирпичиков материи, в частности, протонов, нейтронов, кварков, нейтрино, т.д. Их волновая функция должна быть антисимметричной – если поменять местами два электрона, то волновая функция умножается на -1. Таким образом, существует нулевая вероятность, что два электрона расположатся поверх друг друга, поскольку вероятность этого (и соответствующая волновая функция) равны нулю.

Поэтому потребовалось разработать нейронную сеть нового типа, которая была бы антисимметрична относительно поступающего в нее ввода. Мы назвали ее Fermionic Neural Network или FermiNet. В большинстве квантовохимических методов антисимметрия вводится при помощи функции, именуемой детерминантом. Детерминант – это матрица, обладающая следующим свойством: если поменять местами два ее ряда, то вывод умножается на -1, точно, как волновая функция фермионов. Можно взять набор одноэлектронных функций, рассчитать их для каждого электрона в вашей системе, а затем уложить все результаты в одну матрицу. В таком случае детерминант матрицы будет подлинно антисимметричной волновой функцией. Основное ограничение данного подхода заключается в том, что результирующая функция – именуемая «слэтеровский детерминант» — не слишком широко применима. Волновые функции реальных систем, как правило, гораздо сложнее. Как правило, для исправления этой проблемы берутся большие линейные комбинации слэтеровских детерминантов – иногда миллионы и более – после чего в них вносятся некоторые простые поправки, на основе пар электронов. Даже после этого система может оказаться недостаточно точна для расчета энергий.



Рисунок 2 – слэтеровский детерминант. каждая кривая – это срез, проходящий через одну из орбиталей с рисунка 1. когда электроны 1 и 2 меняются местами, то же происходит и с рядами слэтеровского детерминанта, и волновая функция умножается на -1. так гарантируется соблюдение принципа запрета Паули.

Глубокие нейронные сети зачастую намного превосходят по эффективности линейные комбинации базисных функций при представлении сложных функций. В FermiNet такое превосходство достигается путем внесения каждой из функций в детерминант, функцию всех электронов. Этот метод гораздо мощнее, чем использование одно- и двухэлектронных функций. В FermiNet предусмотрен отдельный информационный поток для каждого электрона. Без учета каких-либо взаимодействий между этими потоками, сеть получилась бы не более выразительной, чем обычный слэтеровский детерминант. Чтобы добиться большего, мы усредняем информацию, собранную от всех потоков на каждом из слоев сети, и передаем эту информацию каждому из потоков на следующий слой. Соответственно, такие потоки обладают подходящими свойствами симметрии, позволяющими создать антисимметричную функцию.

Схожим образом агрегируется информация на каждом из слоев в графовых нейронных сетях. В отличие от слэтеровских детерминантов, сети FermiNet являются универсальными аппроксиматорами функций, как минимум до тех пор, пока слои нейронных сетей остаются достаточно широки. Это означает, что, если нам удастся правильно обучить эти сети, то они смогут выдать практически точное решение уравнение Шрёдингера.



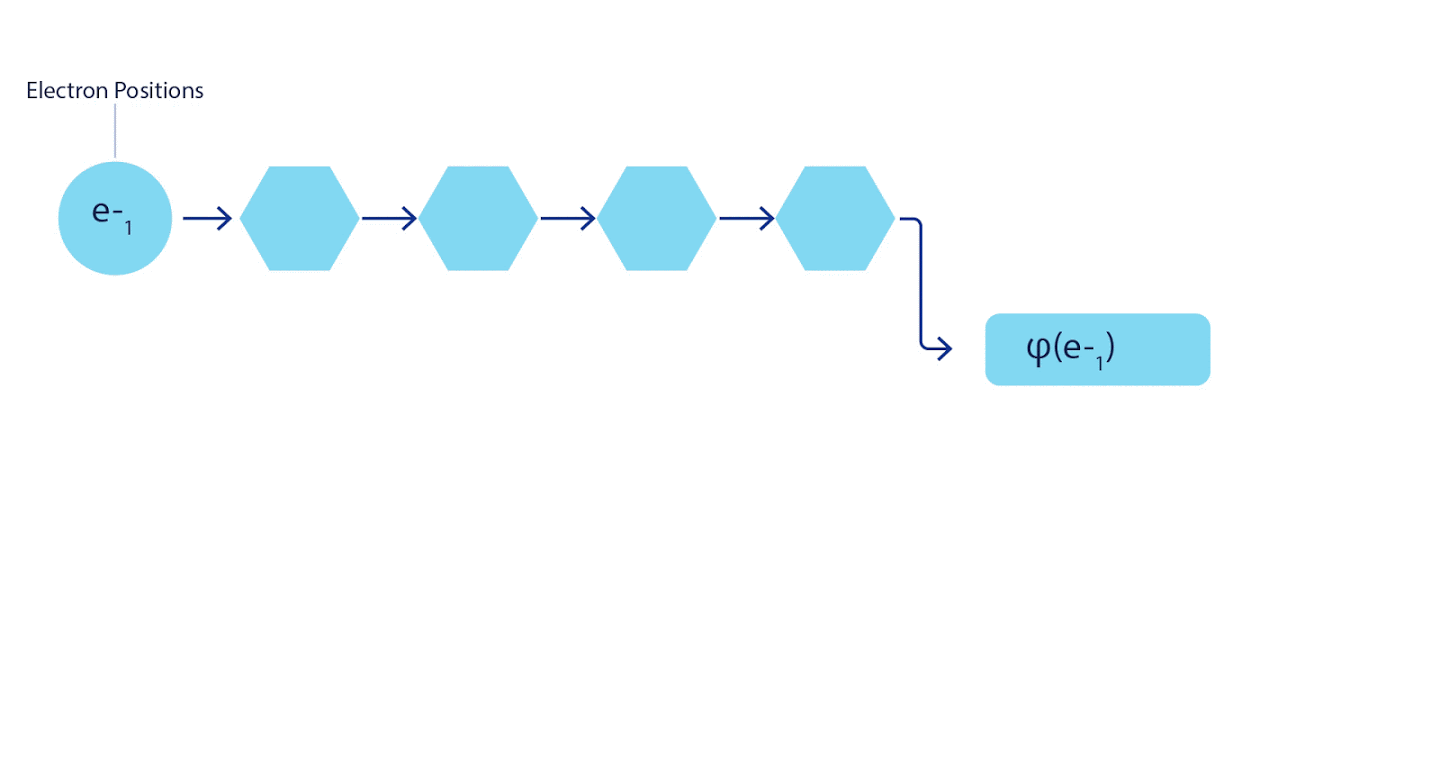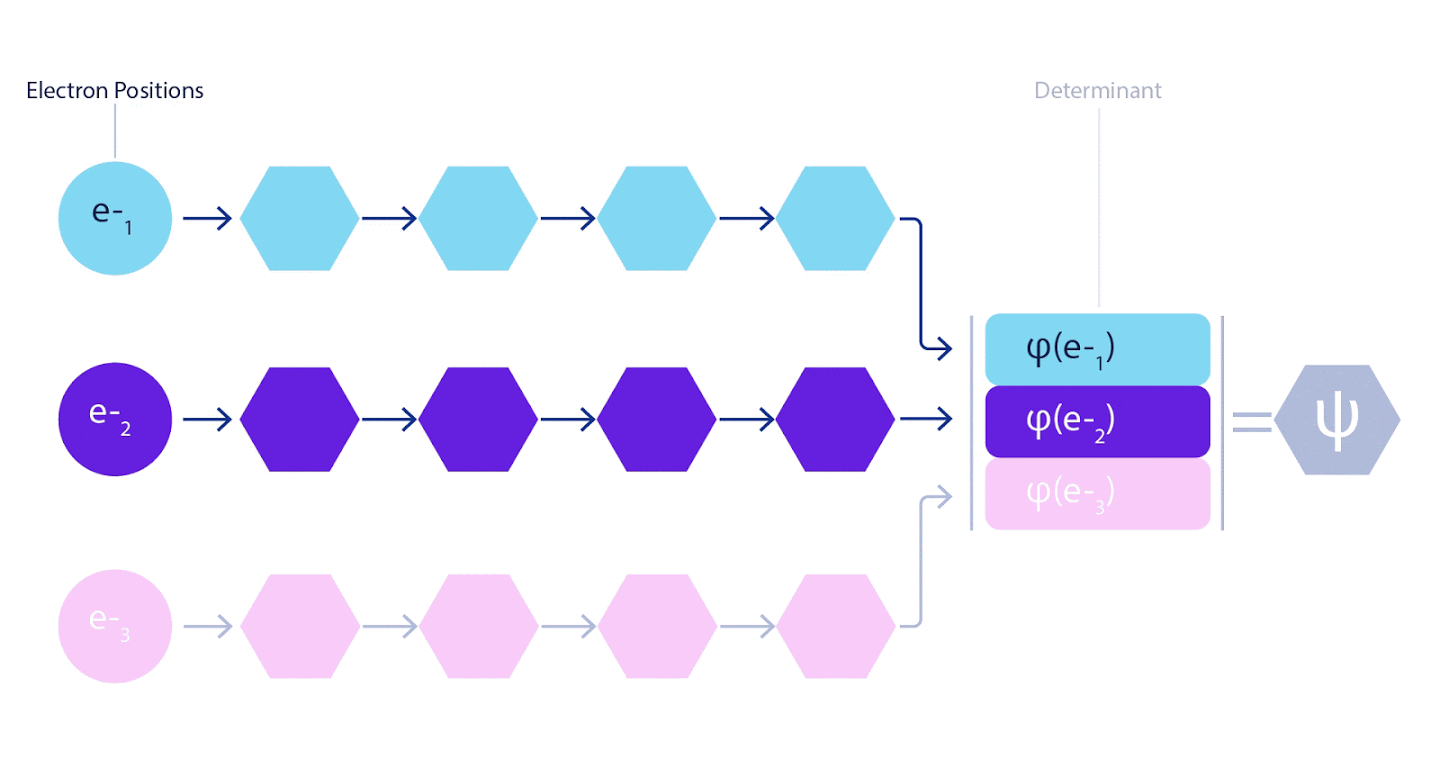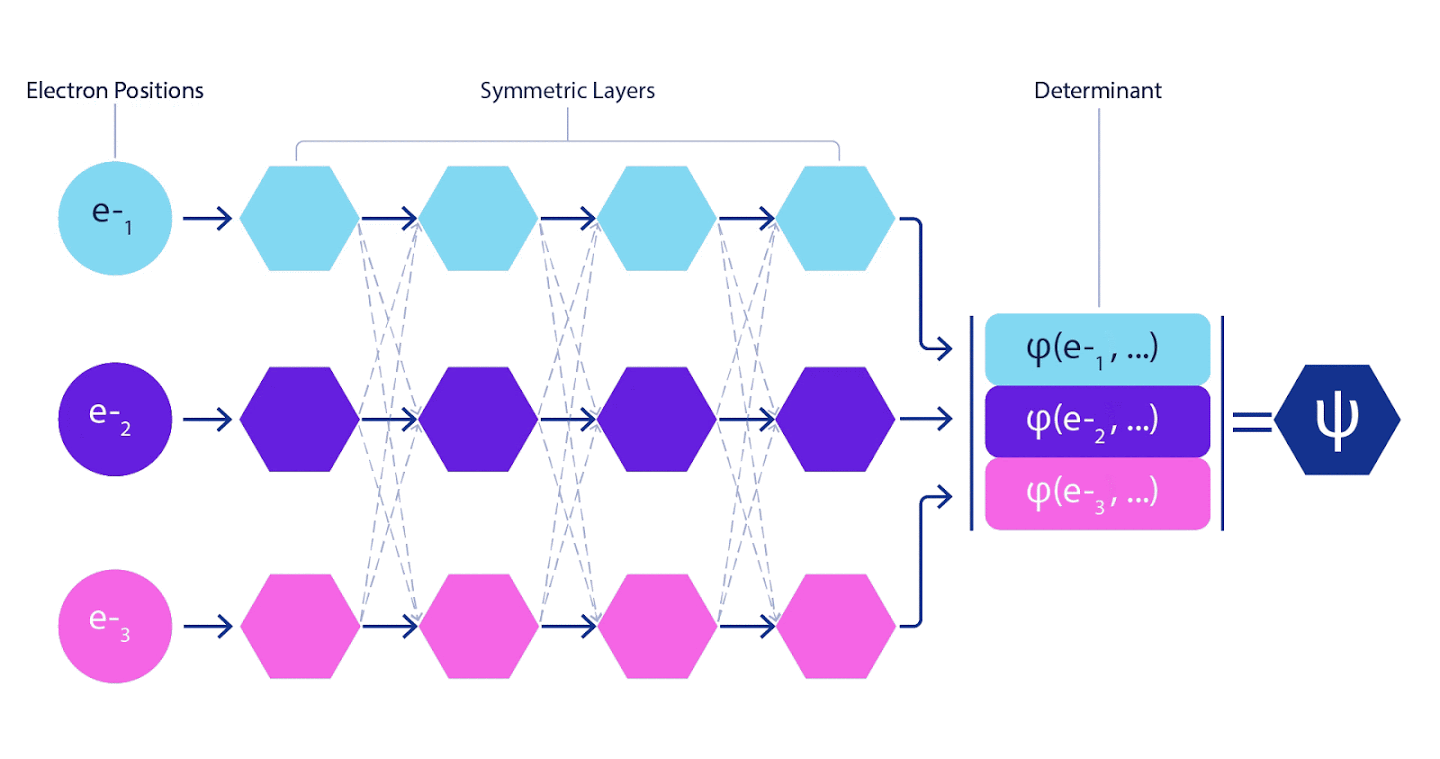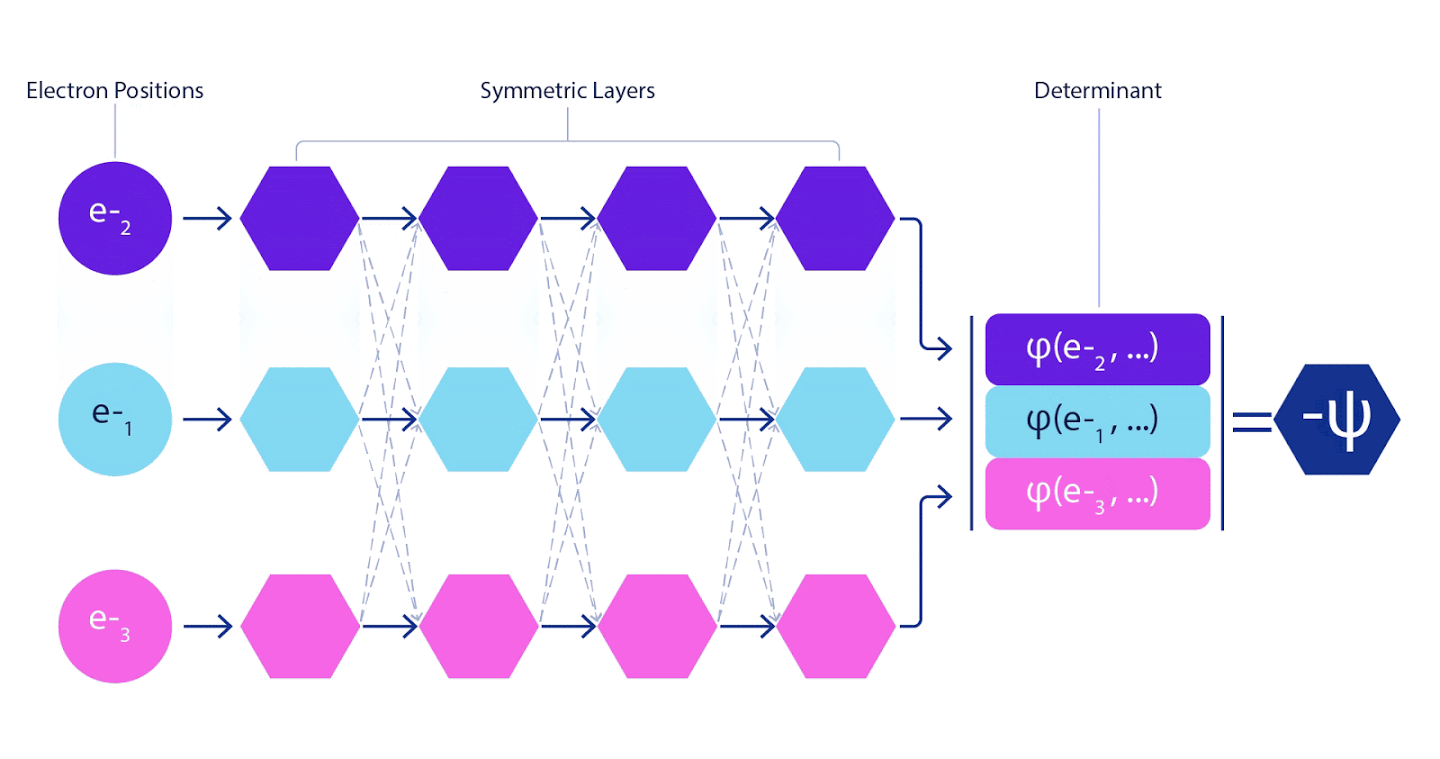
Рисунок 3 – Иллюстрация FermiNet. отдельный поток сети (синий, пурпурный или розовый) функционально очень похож на обычную орбиталь. В FermiNet вводятся симметричные взаимодействия между потоками, что позволяет сделать волновую функцию гораздо более универсальной и выразительной, точно, как обычный слэтеровский детерминант. когда два электрона меняются позициями, это по-прежнему приводит к перестановке двух рядов в детерминанте и к умножению всей волновой функции на -1.

Мы подгоняем сеть FermiNet, минимизируя энергию системы. Чтобы сделать это точно, нам потребовалось бы рассчитать волновую функцию во всех возможных конфигурациях электронов, поэтому нам пришлось бы делать это приблизительно. Поэтому мы берем случайную выборку конфигураций электронов, вычисляем энергию локально при каждом варианте упорядочивания электронов и минимизируем именно эту энергию, а не истинную. Такой метод называется «Монте-Карло», поскольку немного напоминает действия игрока казино, вновь и вновь бросающего кость. Поскольку волновая функция, возведенная в квадрат, дает вероятность наблюдать некоторую конфигурацию частиц в любом месте, наиболее удобно генерировать образцы самой волновой функции – в сущности, имитируя акт наблюдения частиц.

В то время как большинство нейронных сетей обучаются на некоторых внешних данных, в нашем случае нейронная сеть сама генерирует тот ввод, который поступает в нее для обучения. Ситуация немного напоминает вытягивание самого себя за волосы из трясины и означает, что нам не требуется никаких учебных данных кроме позиций тех атомных ядер, вокруг которых пляшут электроны. Базовая идея, известная под названием «вариационный квантовый метод Монте-Карло» (или VMC для краткости) известен в науке с 1960-х и, как правило, считается дешевым, но не очень точным способом расчета энергии системы. Заменив простые волновые функции, основанные на слэтеровских детерминантах, на функции из FermiNet, удалось радикально повысить точность такого подхода на всех рассмотренных нами системах.



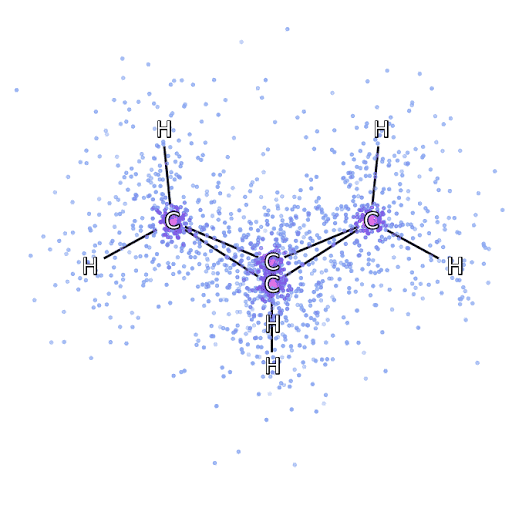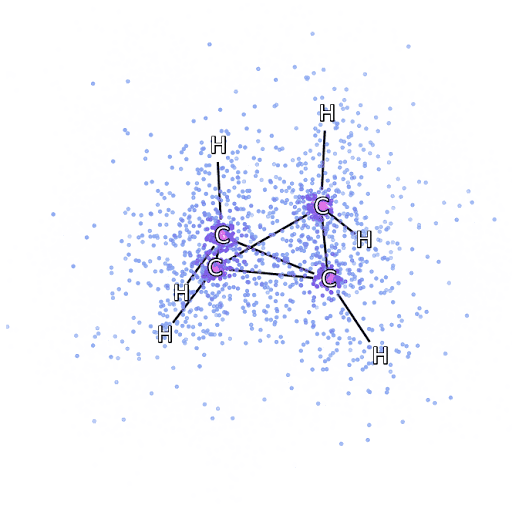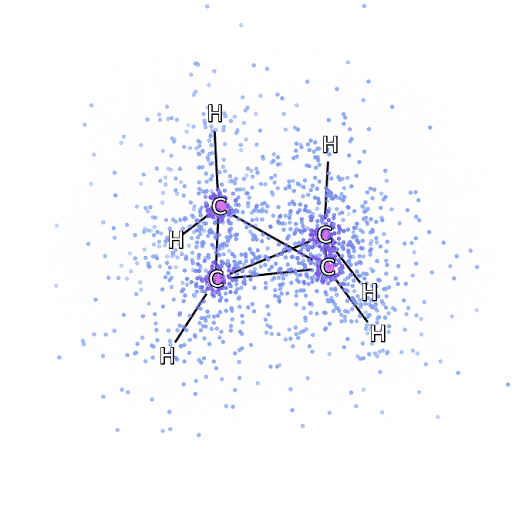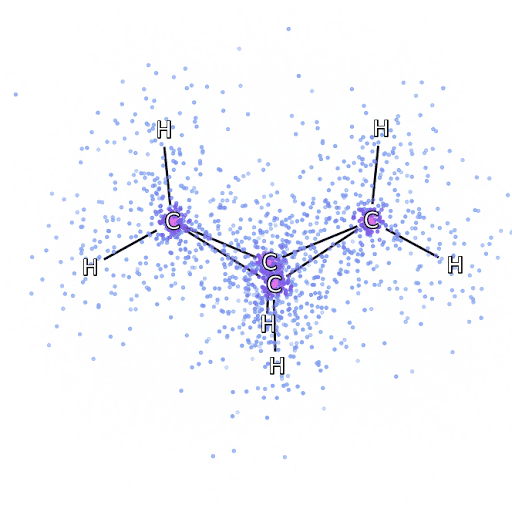
Рисунок 4 – Смоделированные электроны, выбранные из FermiNet, движутся вокруг молекулы бициклобутана.

Чтобы убедиться, что FermiNet действительно является прорывом в своей предметной области, мы начали с исследования простых, хорошо изученных систем, например, атомов из первого ряда периодической таблицы (от водорода до неона). Это небольшие системы — 10 электронов или менее – поэтому они поддаются исследованию при помощи наиболее точными (но усложняющимися по экспоненте) методами. FermiNet намного превосходит сравнимые расчеты VMC, и зачастую позволяет сократить ошибку по сравнению с экспоненциально масштабируемыми расчетами наполовину и более. В более крупных системах методы, усложняющиеся по экспоненте, становятся неприменимы, поэтому в качестве отсчетного мы использовали метод связанных кластеров. Этот метод хорошо работает на молекулах со стабильными конфигурациями, но буксует, когда связи оказываются растянуты или повреждены, а такие факторы критически важны для понимания химических реакций. Притом, что он масштабируется гораздо лучше, чем по экспоненте, тот метод связных кластеров, который был применен в описанном исследовании, всем равно работает как максимум с молекулами средних размеров. Мы применяли FermiNet ко все более крупным молекулам, начиная с гидрида лития и дойдя до бициклобутана – это была самая крупная система, которую мы рассмотрели, в ней 30 электронов. На самых мелких молекулах FermiNet улавливала поразительные 99,8% разницы между энергией связанных кластеров и энергией, получаемой от единственного слэтеровского детерминанта. В случае с бициклобутаном, FermiNet все равно улавливала 97% или более этой корреляционной энергии – огромное достижение для якобы «дешевого, но неточного» подхода.



Рисунок 5 – графическое представление той доли корреляционной энергии, которую FermiNet верно улавливает при работе с молекулами. Пурпурная планка отмечает показатель в 99% корреляционной энергии. Слева направо: гидрид лития, азот, этилен, озон, этанол и бициклобутан.

Тогда как методы связанных кластеров хорошо работают со стабильными молекулами, настоящий «передний край» вычислительной химии связан с пониманием того, как молекулы растягиваются, скручиваются и рвутся. При решении таких задач методы связных кластеров часто сбоят, поэтому приходится сравнивать результат с как можно более многочисленными контрольными образцами, чтобы убедиться в непротиворечивости полученного ответа. В рамках описанного опыта были рассмотрены две контрольные растянутые системы – молекула азота (N₂) и цепочка водорода из 10 атомов (H₁₀). В молекуле азота особенно сложная связь, поскольку от каждого атома в ней участвует по 3 электрона.

Водородная цепочка, в свою очередь, интересна для понимания того, какие свойства электроны проявляют в материалах, например, чтобы спрогнозировать, будет данный материал проводить электричество или нет. В обеих системах метод связных кластеров хорошо работал в состоянии равновесия, но сталкивался со сложностями, когда связи растягивались. Традиционные методы VMC плохо работали во всем диапазоне примеров. Но FermiNet оказался среди самых лучших методов из всех исследованных, независимо от длины связи.

Заключение

Полагаем, FermiNet – это начало больших достижений в области синтеза методов глубокого обучения и вычислительной квантовой химии. Большинство систем, с которыми до сих пор была рассмотрена FermiNet, хорошо изучены и понятны. Но, точно как первые хорошие результаты с применением глубокого обучения в других предметных областях стимулировали всплеск дальнейших исследований и стремительный прогресс, можно надеяться, что то же произойдет и с FermiNet, и появятся идеи для новых, еще более качественных архитектур нейронных сетей. Уже после того, как описанная работа была выложена на arXiv, другие группы поделились своими подходами к применению глубокого обучения для решения задач, в которые вовлечены множества электронов. Кроме того, пока мы только едва копнули вычислительную квантовую физику и планируем применить FermiNet для решения сложных задач в области материаловедения и физики твердого тела.

Научная статья находится здесь, а код можно посмотреть здесь. Авторы благодарят Джима Кинвина, Адама Кайна и Доминика Барлоу за помощь в подготовке рисунков.