Всем привет! Меня зовут Дмитрий Руднев, я frontend-разработчик в компании БКС. Начинал я свой путь с верстки интерфейсов различной сложности и всегда уделял повышенное внимание именно интерфейсу: насколько пользователю будет комфортно с ним взаимодействовать, смог ли я донести до пользователя тот самый интерфейс, каким его задумал дизайнер.
В этой серии статей я хочу поделиться своим опытом применения функциональных практик во frontend-разработке расскажу про плюсы и минусы, которые вы получите как разработчик, используя эти практики. Если тема вам понравится, то мы погрузимся в более «сухие» и сложные уголки функционального мира. Сразу отмечу, что пойдем мы от большего к меньшему, то есть посмотрим на классическое приложение c высоты птичьего полета, а по мере прохождения статей будем спускаться туда, где конкретная практика принесет нам заметную пользу.
Итак, начнем с обработки состояний. Заодно расскажу, причем тут вообще монады и функторы.
При разгадке очередного интерфейса и нахождения точек соприкосновения между UI и аналитикой я стал замечать, что каждый раз, когда разработчик имеет дело с сетью, ему просто необходимо обрабатывать все состояния UI и описывать реакцию на то или иное состояние. А так как каждый из нас стремится к совершенству, то возникает желание под этот способ обработки состояний вывести какой-то паттерн, который максимально прозрачно опишет то, что вообще происходит и что является инициатором той или иной реакции, а как следствие — результатом работы. К счастью, в мире программирование почти всё, о чем вы можете подумать, было кем-то реализовано до вас.
Как в мире разработки, так и в мире дизайна формировались не только паттерны, позволяющие эффективно решить ваши задачи, но и антипаттеры, которых следует избегать всеми силами для того, чтобы плохая практика не процветала, и разработчик или дизайнер всегда имели точку опоры в ситуациях, когда нет конкретного решения.
В нашем случае ситуация, которая возникает у большинства разработчиков, — обработка всех состояний UI-элемента и реакция на них. Проблема тут в том, что UI-элемент может взаимодействовать как с локальным состоянием (без выполнения асинхронных запросов), так и с удаленными ресурсами или хранилищами. Разработчики порой забывают обработать все краевые случаи, что приводит к неконсистентному поведению системы в целом.
Рассмотрим самый простой пример, где у нас есть список элементов, который мы запрашиваем с сервера, и нам нужно корректно отобразить UI в соответствии с результатом запроса. Нас интересует функция
На примере наглядно видно, что за каждое состояние модели данных отвечает своя функция, и каждая функция возвращает предписанный ей фрагмент UI (сообщение, кнопку и прочее). Забегая вперед, скажу, что в примере используется
Вот так элегантно, а главное безопасно мы можем работать с данными и реагировать на них. Это была вводная часть, где я попытался продемонстрировать преимущества функционального подхода в таком, казалось бы простом примере.
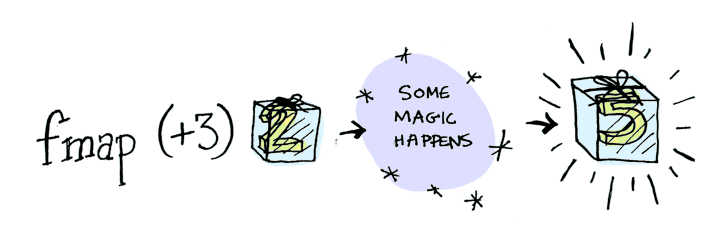
А теперь начнем постепенно погружаться в прикладную теорию категорий и разберем такие понятия как
«По существу, функтор является не более, чем структурой данных, позволяющей применять функции преобразования с целью извлечь значения из оболочки, модифицировать их, а затем поместить их обратно в оболочку.
Заключение значений в оболочку или контейнер является основополагающим проектным шаблоном в функциональном программировании, поскольку оно защищает от прямого доступа к значениям, позволяя безопасно и неизменяемо манипулировать ими в прикладных программах.»
Эту цитату я взял из замечательной книги по рассмотрению методик функционального программирования на JavaScript. Начнем с теоретической составляющей и разберем, что на самом деле являет собой функтор. Для начала нам нужно на самом базовом уровне познакомиться с увлекательным разделом математики под названием теория категорий.
Теория категорий — раздел математики, изучающий свойства отношений между математическими объектами, не зависящие от внутренней структуры объектов. Теория категорий занимает центральное место в современной математике, она также нашла применения в информатике, логике и в теоретической физике.
Категория состоит из объектов и стрелок, которые направлены между ними. Легче всего представить категорию графически:
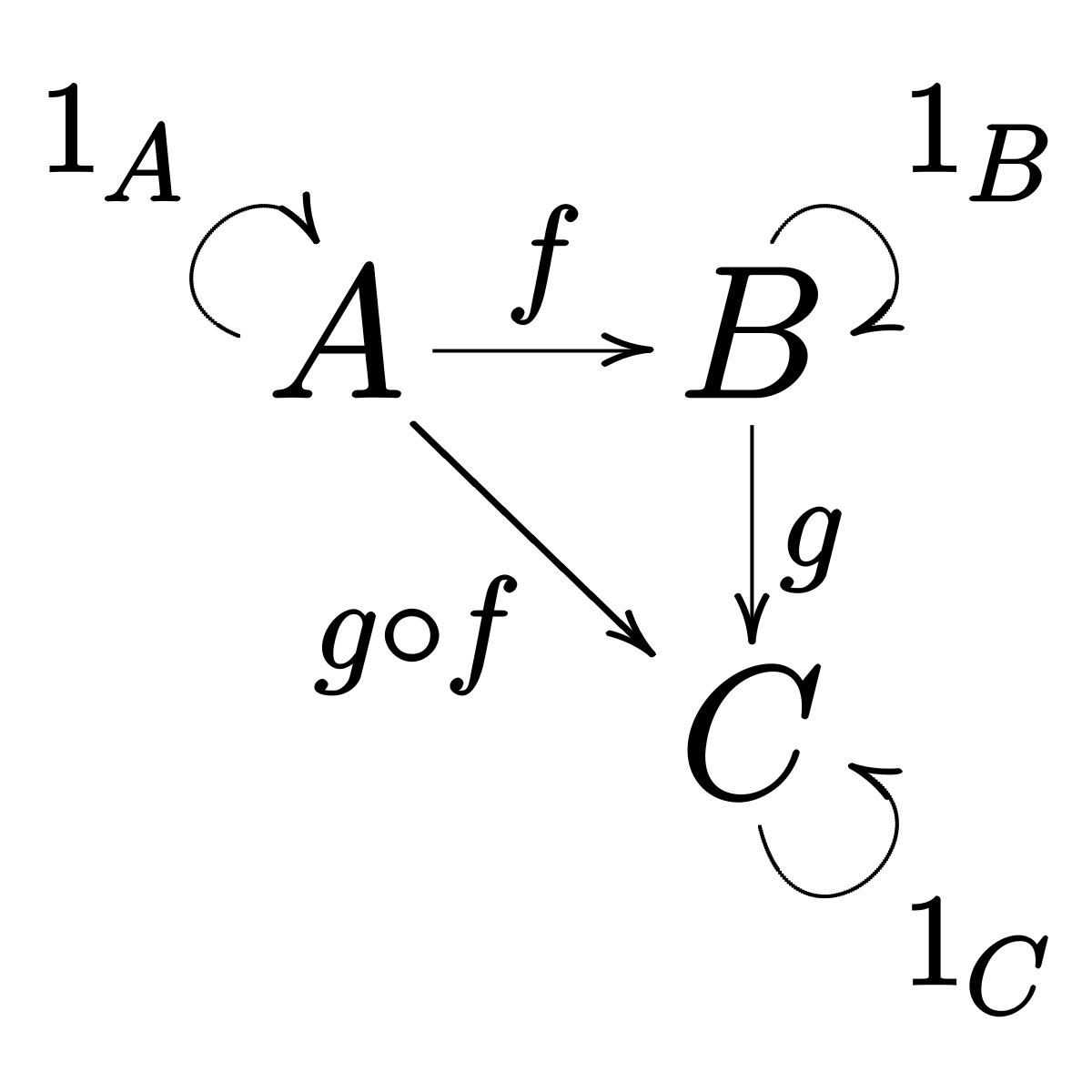
Стрелки компонуются так, что если у вас есть стрелка от объекта А к объекту B и стрелка от объекта B к C, то должна быть и стрелка — их композиция от A к C. Думайте о стрелках как о функциях; ещё их называют морфизмами. У вас есть функция
В математике композиция направлена справа налево. В этом случае помогает, если вы читаете g ◦ f как «g после f».
Есть два очень важных свойства, которым композиция должны удовлетворять в любой категории.
Теперь мы можем рассмотреть, что такое функтор в теории категорий.
Функтор — особый тип отображений между категориями. Его можно понимать как отображение, сохраняющее структуру. Функторы между малыми категориями являются морфизмами в категории малых категорий. Совокупность всех категорий не является категорией в обычном смысле, так как совокупность её объектов не является классом. – Википедия.
Рассмотрим пример реализации функтора для контейнера Maybe, представляющего собой идею «значения, которое может отсутствовать».
Метод
Действительно, если немного по-другому расставить скобки в интерфейсе, мы можем получить такую сигнатуру функции
Определив интерфейс:
мы получим такое определение
Этот простой трюк позволяет думать о функторе как о способе «поднять в контекст контейнера» чистую функцию. Благодаря этому можно безопасным способом работать с данными разного рода: например, успешно обрабатывать цепочки необязательных вложенных значений; преобразовывать списки данных; обрабатывать исключения и многое другое.
Как пояснялось ранее, с помощью функторов можно применять функции к значениям безопасно и неизменяемо. Монады подобны функторам, за исключением того, что они способны делегировать специальную логику в особых случаях. Самому функтору известно лишь, как применять данную функцию и заключать полученный результат обратно в оболочку, а дополнительная логика у него отсутствует.
Монада возникает при создании целого типа данных по принципу извлечения данных по принципу извлечения значений из оболочек и определения правил из вложенности. Подобно функторам, монады являются проектным шаблоном, применяемым для описания вычислений в виде последовательности стадий, где вообще неизвестно обрабатываемое значение, но именно монады дают возможность безопасно и без побочных эффектов управлять потоком данных, когда они применяются в композиции. Монады могут быть направлены на решение самых разных задач. Теоретически монады зависят от системы типов в конкретном языке. В действительности многие считают, что их можно понять лишь в том случае, если имеются явные типы данных.
Для того чтобы лучше понять монады, необходимо усвоить следующие важные понятия.
А вот практические примеры применения данных свойств функтора и других теоретико-категорных конструкций я покажу в будущих статьях.

В этой серии статей я хочу поделиться своим опытом применения функциональных практик во frontend-разработке расскажу про плюсы и минусы, которые вы получите как разработчик, используя эти практики. Если тема вам понравится, то мы погрузимся в более «сухие» и сложные уголки функционального мира. Сразу отмечу, что пойдем мы от большего к меньшему, то есть посмотрим на классическое приложение c высоты птичьего полета, а по мере прохождения статей будем спускаться туда, где конкретная практика принесет нам заметную пользу.
Итак, начнем с обработки состояний. Заодно расскажу, причем тут вообще монады и функторы.
Intro
При разгадке очередного интерфейса и нахождения точек соприкосновения между UI и аналитикой я стал замечать, что каждый раз, когда разработчик имеет дело с сетью, ему просто необходимо обрабатывать все состояния UI и описывать реакцию на то или иное состояние. А так как каждый из нас стремится к совершенству, то возникает желание под этот способ обработки состояний вывести какой-то паттерн, который максимально прозрачно опишет то, что вообще происходит и что является инициатором той или иной реакции, а как следствие — результатом работы. К счастью, в мире программирование почти всё, о чем вы можете подумать, было кем-то реализовано до вас.
Как в мире разработки, так и в мире дизайна формировались не только паттерны, позволяющие эффективно решить ваши задачи, но и антипаттеры, которых следует избегать всеми силами для того, чтобы плохая практика не процветала, и разработчик или дизайнер всегда имели точку опоры в ситуациях, когда нет конкретного решения.
В нашем случае ситуация, которая возникает у большинства разработчиков, — обработка всех состояний UI-элемента и реакция на них. Проблема тут в том, что UI-элемент может взаимодействовать как с локальным состоянием (без выполнения асинхронных запросов), так и с удаленными ресурсами или хранилищами. Разработчики порой забывают обработать все краевые случаи, что приводит к неконсистентному поведению системы в целом.
Все примеры будут содержать примеры кода с использованием библиотеки React и надмножеством языка JavaScript — TypeScript, а также библиотеки для функционального программирования fp-ts.
Рассмотрим самый простой пример, где у нас есть список элементов, который мы запрашиваем с сервера, и нам нужно корректно отобразить UI в соответствии с результатом запроса. Нас интересует функция
render, потому что в ней нам необходимо по ходу выполнения запроса отображать корректное состояние. Полный код примера можно посмотреть по ссылке: simple application. В дальнейшем там будет доступен полный проект, ориентированный на цикл статей, где по ходу мы будем разбирать отдельные его части. const renderInitial = (...) => ...;
const renderPending = (...) => ...;
const renderError = (...) => ... ;
const renderSuccess = (...) => ... ;
return (
{state.subcribers.foldL(
renderInitial,
renderPending,
renderError,
renderSuccess,
)}
);
На примере наглядно видно, что за каждое состояние модели данных отвечает своя функция, и каждая функция возвращает предписанный ей фрагмент UI (сообщение, кнопку и прочее). Забегая вперед, скажу, что в примере используется
RemoteData monad.Вот так элегантно, а главное безопасно мы можем работать с данными и реагировать на них. Это была вводная часть, где я попытался продемонстрировать преимущества функционального подхода в таком, казалось бы простом примере.
Functor и Monad
А теперь начнем постепенно погружаться в прикладную теорию категорий и разберем такие понятия как
Functor и Monad, а также рассмотрим практики по безопасной работе с данными, используя функциональные практики.«По существу, функтор является не более, чем структурой данных, позволяющей применять функции преобразования с целью извлечь значения из оболочки, модифицировать их, а затем поместить их обратно в оболочку.
Заключение значений в оболочку или контейнер является основополагающим проектным шаблоном в функциональном программировании, поскольку оно защищает от прямого доступа к значениям, позволяя безопасно и неизменяемо манипулировать ими в прикладных программах.»
Эту цитату я взял из замечательной книги по рассмотрению методик функционального программирования на JavaScript. Начнем с теоретической составляющей и разберем, что на самом деле являет собой функтор. Для начала нам нужно на самом базовом уровне познакомиться с увлекательным разделом математики под названием теория категорий.
Теория категорий — раздел математики, изучающий свойства отношений между математическими объектами, не зависящие от внутренней структуры объектов. Теория категорий занимает центральное место в современной математике, она также нашла применения в информатике, логике и в теоретической физике.
Категория состоит из объектов и стрелок, которые направлены между ними. Легче всего представить категорию графически:
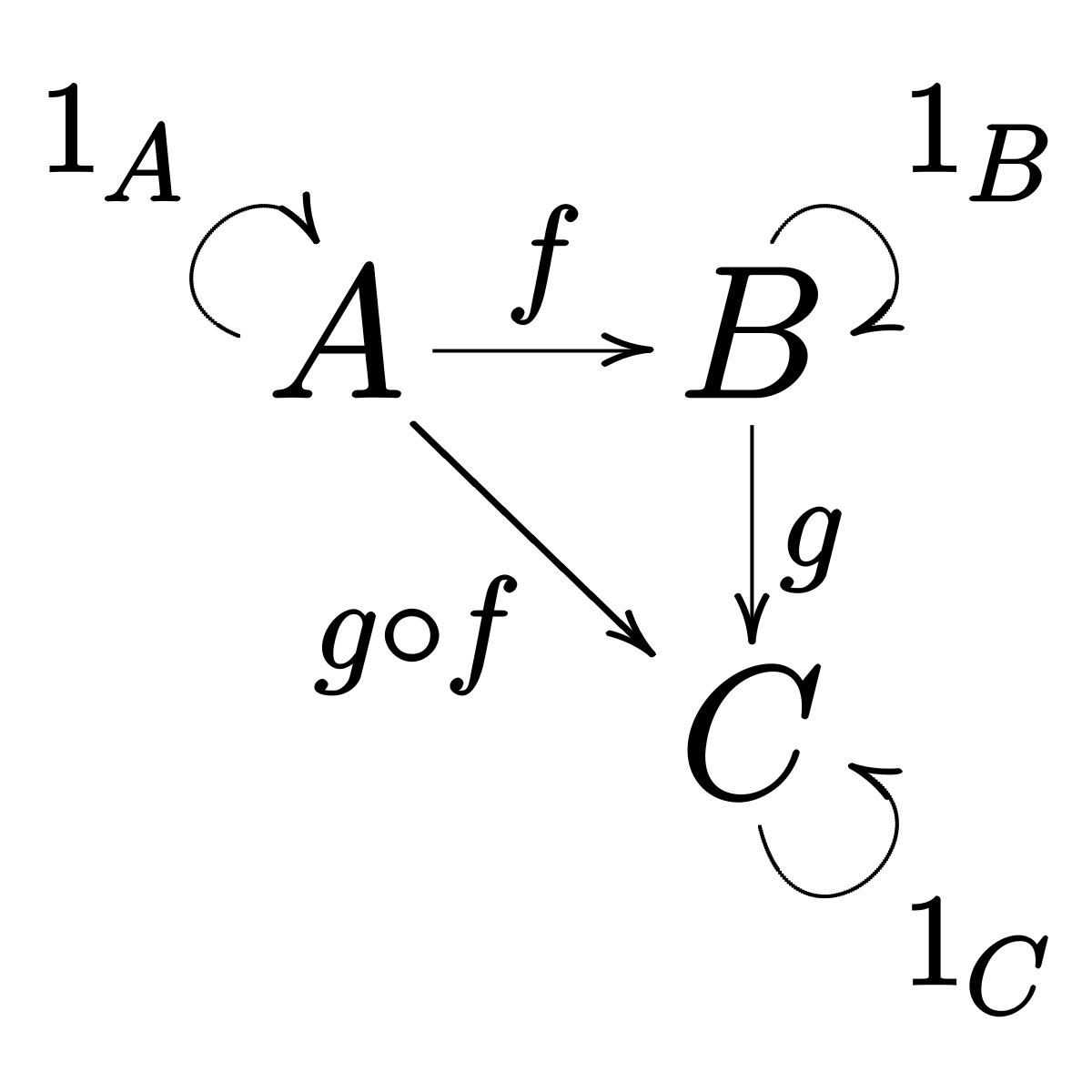
Стрелки компонуются так, что если у вас есть стрелка от объекта А к объекту B и стрелка от объекта B к C, то должна быть и стрелка — их композиция от A к C. Думайте о стрелках как о функциях; ещё их называют морфизмами. У вас есть функция
f , которая принимает в качестве аргумента A, а возвращает B. Ещё есть другая функция g, которая принимает в качестве аргумента B и возвращает C. Вы можете объединить их, передавая результат из f в g. Мы только что описали новую функцию, которая принимает A и возвращает C. В математике такая композиция обозначается небольшим кружком между обозначениями функций: g ◦ f. Обратите внимание на порядок композиции — справа налево. В математике композиция направлена справа налево. В этом случае помогает, если вы читаете g ◦ f как «g после f».
-—объявление функции от A к B
f :: A -> B
-—объявление функции от B к С
g :: B -> C
-—Композиция A к C
g . f
Есть два очень важных свойства, которым композиция должны удовлетворять в любой категории.
- Композиция ассоциативна (ассоциативность — свойство операций, позволяющее восстановить последовательность их выполнения при отсутствии явных указаний на очерёдность при равном приоритете; при этом различается левая ассоциативность, при которой вычисление выражения происходит слева направо, и правая ассоциативность — справа налево. Соответствующие операторы называют левоассоциативными и правоассоциативными. Если у вас есть три морфизма (стрелки), f, g и h, которые могут быть скомпонованы (то есть их типы согласованы друг с другом) вам не нужны скобки чтобы сгруппировать их. Математически это записывается так
h ◦ (g ◦ f) = (h ◦ g) ◦ f = h ◦ g ◦ f - Для каждого объекта A есть стрелка, которая будет единицей композиции. Эта стрелка от объекта к самому себе. Быть единицей композиции — значит, что при композиции единицы с любой стрелкой, которая, либо начинается на A, либо заканчивается на A соответственно, композиция возвращает ту же стрелку. Единичная стрелка объекта A называется IDa (единица на A). В математической нотации, если f идет от A к B, то
f ◦ idA = f
Для работы с функциями единичная стрелка реализована в виде тождественной функции, которая просто возвращает свой аргумент.
Теперь мы можем рассмотреть, что такое функтор в теории категорий.
Функтор — особый тип отображений между категориями. Его можно понимать как отображение, сохраняющее структуру. Функторы между малыми категориями являются морфизмами в категории малых категорий. Совокупность всех категорий не является категорией в обычном смысле, так как совокупность её объектов не является классом. – Википедия.
Рассмотрим пример реализации функтора для контейнера Maybe, представляющего собой идею «значения, которое может отсутствовать».
const compose = <A, B, C>(
f: (a: A) => B,
g: (b: B) => C,
): (a: A) => C => (a: A) => g(f(a));
// Контейнер Maybe:
type Nothing = Readonly<{ tag: 'Nothing' }>;
type Just<A> = Readonly<{ tag: 'Just'; value: A }>;
export type Maybe<A> = Nothing | Just<A>;
const nothing: Nothing = { tag: 'Nothing' };
const just = <A>(value: A): Just<A> => ({ tag: 'Just', value });
// Функтор для контейнера Maybe:
const fmap = <A, B>(f: (a: A) => B) =>
(fa: Maybe<A>): Maybe<B> => {
switch (fa.tag) {
case 'Nothing':
return nothing;
case 'Just':
return just(f(fa.value));
}
};
// Закон 1: fmap id === id
namespace Laws {
console.log(
fmap(id)(just(42)),
id(just(42)),
); // => { tag: 'Just', value: 42 }
// Закон 2: fmap f ◦ fmap g === fmap (f ◦ g)
const f = (a: number): string => `Got ${a}!`;
const g = (s: string): number => s.length;
console.log(
compose(fmap(f), fmap(g))(just(42)),
fmap(compose(f, g))(just(42)),
); // => { tag: 'Just', value: 7 }
}
Метод
fmap можно рассматривать с двух сторон:- Как способ применить чистую функцию к «контейнеризированному» значению;
- Как способ «поднять в контекст контейнера» чистую функцию.
Действительно, если немного по-другому расставить скобки в интерфейсе, мы можем получить такую сигнатуру функции
fmap:const fmap: <A, B>(f: (a: A) => B) => ((ma: Maybe<A>) => Maybe<B>);
Определив интерфейс:
type Function1<Domain, Codomain> = (a: Domain) => Codomain;
мы получим такое определение
fmap:const fmap: <A, B>(f: (a: A) => B) => Function1<Maybe<A>, Maybe<B>>;
Этот простой трюк позволяет думать о функторе как о способе «поднять в контекст контейнера» чистую функцию. Благодаря этому можно безопасным способом работать с данными разного рода: например, успешно обрабатывать цепочки необязательных вложенных значений; преобразовывать списки данных; обрабатывать исключения и многое другое.
Как пояснялось ранее, с помощью функторов можно применять функции к значениям безопасно и неизменяемо. Монады подобны функторам, за исключением того, что они способны делегировать специальную логику в особых случаях. Самому функтору известно лишь, как применять данную функцию и заключать полученный результат обратно в оболочку, а дополнительная логика у него отсутствует.
Монада возникает при создании целого типа данных по принципу извлечения данных по принципу извлечения значений из оболочек и определения правил из вложенности. Подобно функторам, монады являются проектным шаблоном, применяемым для описания вычислений в виде последовательности стадий, где вообще неизвестно обрабатываемое значение, но именно монады дают возможность безопасно и без побочных эффектов управлять потоком данных, когда они применяются в композиции. Монады могут быть направлены на решение самых разных задач. Теоретически монады зависят от системы типов в конкретном языке. В действительности многие считают, что их можно понять лишь в том случае, если имеются явные типы данных.
Для того чтобы лучше понять монады, необходимо усвоить следующие важные понятия.
Монада. Предоставляет абстрактный интерфейс для монадических операций
Монадический тип. Конкретная реализация данного интерфейса
А вот практические примеры применения данных свойств функтора и других теоретико-категорных конструкций я покажу в будущих статьях.