Визуализация многомерных данных очень полезна для выявления их важных закономерностей и свойств. Для этой цели используются алгоритмы снижения размерности. Среди наиболее распространенных алгоритмов можно отметить метод главных компонент (англ. principal component analysis, PCA) и стохастическое вложение соседей с t-распределением (англ. t-distributed Stochastic Neighbor Embedding, t-SNE). Оба этих алгоритма обладают высокой временной сложностью: у PCA, у t-SNE, где — количество объектов. К тому же у t-SNE есть по меньшей мере 3 гиперпараметра, к подбору которых он очень чувствителен. Я хочу вам рассказать о новом алгоритме полигональной системы координат (англ. polygonal coordinate system, PCS). Это алгоритм без гиперпараметров и со сложностью от числа объектов.
Полигональная система координат (PCS) — это способ представить входные вектора размерности на двумерной плоскости. Для этой цели в -мерном пространстве признаков вещественные точки представляются в виде правильных многоугольников с сторонами длины на плоскости, обозначается как . Его также называют межпространством, промежуточной стадией между большой размерностью и двумерной плоскостью. Многоугольники со сторонами 1 называются унитарными и обозначаются как или просто .

Результирующее двумерное пространство задается двумя осями — горизонтальная и вертикальная . Каждая сторона многоугольника представляет собой одну координату изначального -мерного пространства. На рисунке выше представлены два многоугольника для (a) 3-мерного пространства признаков и (b) 6-мерного пространства. На рисунке — это метавектор, то есть задает множество векторов в одном направлении, но различной длины. Он обозначает проекцию -й координаты точки на -ю сторону многоугольника.
Алгоритм PCS состоит из трех шагов:
1) Нормализация данных
2) Проекция данных в межпространство
3) Проекция на плоскость.
Это самый простой шаг и заключается в min-max нормализации признаков:
Эта нормализация нужна, чтобы результирующий многоугольник был унитарным и правильным.
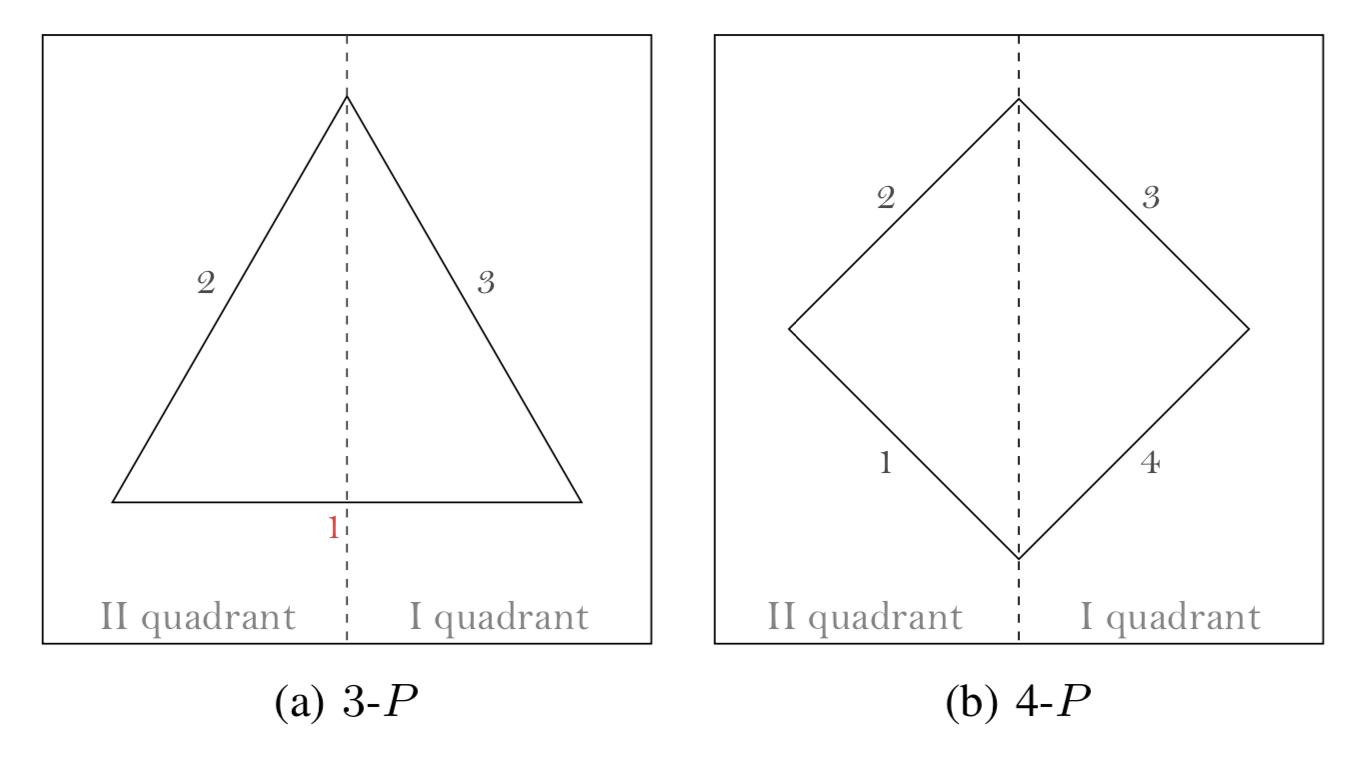
Рассмотрим угол на рисунке выше. — это угол от оси до в положительном направлении. Он равен (a) и (b) . При этом каждый вектор будет образовывать такой угол , отсюда получаем последовательность из углов, считая по часовой стрелке. Первый угол в последовательности будет наибольшим и выражается как функция от внутреннего угла многоугольника как . Так как позиция угла в последовательности важна, то нумерацию сторон многоугольника осуществим по правилу: начинать снизу многоугольника со второго квадранта и двигаться по часовой стрелке:
Тогда последовательность углов определяется так:
Описание алгоритма
Полигональная система координат (PCS) — это способ представить входные вектора размерности на двумерной плоскости. Для этой цели в -мерном пространстве признаков вещественные точки представляются в виде правильных многоугольников с сторонами длины на плоскости, обозначается как . Его также называют межпространством, промежуточной стадией между большой размерностью и двумерной плоскостью. Многоугольники со сторонами 1 называются унитарными и обозначаются как или просто .

Результирующее двумерное пространство задается двумя осями — горизонтальная и вертикальная . Каждая сторона многоугольника представляет собой одну координату изначального -мерного пространства. На рисунке выше представлены два многоугольника для (a) 3-мерного пространства признаков и (b) 6-мерного пространства. На рисунке — это метавектор, то есть задает множество векторов в одном направлении, но различной длины. Он обозначает проекцию -й координаты точки на -ю сторону многоугольника.
Алгоритм PCS состоит из трех шагов:
1) Нормализация данных
2) Проекция данных в межпространство
3) Проекция на плоскость.
Шаг 1. Нормализация данных
Это самый простой шаг и заключается в min-max нормализации признаков:
Эта нормализация нужна, чтобы результирующий многоугольник был унитарным и правильным.
Шаг 2. Проекция данных в межпространство
Рассмотрим угол на рисунке выше. — это угол от оси до в положительном направлении. Он равен (a) и (b) . При этом каждый вектор будет образовывать такой угол , отсюда получаем последовательность из углов, считая по часовой стрелке. Первый угол в последовательности будет наибольшим и выражается как функция от внутреннего угла многоугольника как . Так как позиция угла в последовательности важна, то нумерацию сторон многоугольника осуществим по правилу: начинать снизу многоугольника со второго квадранта и двигаться по часовой стрелке:

Тогда последовательность углов определяется так:




