Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
14го декабря в одном из самых авторитетных общенаучных журналов Nature была опубликована статья с, кажется, сенсационным заголовком: «ИИ-модели Google DeepMind превосходят математиков в решении нерешённых проблем». А в блогпосте дочки гугла и вовсе не постеснялся указать, что это — первые находки Больших Языковых Моделей (LLM) в открытых математических проблемах. Неужели правда? Или кликбейт — и это в Nature? А может мы и вправду достигли техносингулярности, где машины двигают прогресс? Что ж, давайте во всём разбираться!

Всем привет! Статья ниже — подробный разбор достаточно сложного топика, и в некоторых моментах нужно будет сосредоточиться и вдумчиво читать. Я постарался представить все важные аспекты как можно проще, но в то же время не теряя общности и глубины. Перед прочтением рекомендуется ознакомитьcя с принципами работы больших языковых моделей, о чём я уже писал на Хабре (даже вошло в лучшее за 2023й!).
Содержание
Предисловие
Карты, точки, три столпа: настольные игры и наука
Задача об упаковке в контейнеры
Пятиминутка про LLM'ки
Снятся ли LLM'кам обезьяны?
Начинаем генерацию
Сработало ли?
А что дальше? — Вместо заключения
Предисловие
Large Language Models (LLM, или Большие Языковые Модели по-русски) в последний год показали себя в роли полезных ассистентов, а про ChatGPT в наших кругах не говорил только ленивый. Эти нейросети хороши за счёт того, что предоставляют удобный чат-интерфейс к аггрегированной со всего света информации, при этом они способы отвечать не только кусочками текста с сайтов, но и в любом произвольном удобоваримом виде. Они же пишут код в помощь разработчикам, да и в целом помогают решать разного рода проблемы.
За последние месяцы вокруг этих моделей поднялась ещё большая шумиха — регуляции нейронок обсуждают на самых высших уровнях, видя потенциальные угрозы. Совсем недавно Белый Дом, а затем и Европарламент выпустили документы, задающие границы технологии. Однако для многих остаётся загадкой — а чего в общем-то бояться? Как чатботы могут нанести вред? И уж тем более смешными выглядят попытки показать, что в GPT-подобных системах есть «интеллект» (зачастую без возможности дать формальное определение). Многие считают, что ChatGPT лишь воспроизводит информацию, которую прочитал в интернете во время тренировки. Простой «статистический попугай», выкрикивающий фразы (не)впопад. Но могут ли LLM порождать новые знания, которые точно не были известны человечеству заранее?
На этот вопрос ещё сложнее ответить, если учесть, что модели часто «галлюцинируют», то есть на серьёзных щах пишут вещи, которые не имеют смысла или являются неточными. С одной стороны, они не всегда отвечают то же, что ответил бы человек, а с другой — бредят. Но что, если бы мы могли использовать этот «творческий» потенциал во благо, выявляя и развивая лишь лучшие и корректно сгенерированные идеи?
Этим вопросом задаются ведущие исследовательские лаборатории, от OpenAI до DeepMind. Последние и опубликовали статью под названием «Mathematical discoveries from program search with large language models», ставшей основой для этого поста.
И немного забегая вперёд, но чтобы развеять ауру мистики вокруг, давайте сразу проговорим: да, действительно, программа на языке программирования Python, сгенерированная LLM'кой, дала решение, которое не было известно человечеству до этого. Более того, это решение лучше, чем найденные учёными за десятилетия. И это даже не третьесортная проблема — Теренс Тао называл её своим любимым открытым вопросом математики. Теренс — это лауреат Филдсовской премии (аналог Нобелевской, но для математики), а также самый молодой участник, призёр и победитель Международной олимпиады по математике. В общем, Тао падок на драгоценные металлы в медалях, и к его словам можно прислушиваться — так что у нас тут всё серьёзно.

Перед тем, как начать разбирать «научный прорыв» и работу научных систем на основе LLM, хорошо бы понять — а что вообще за проблема перед нами стоит? Есть пара хороших новостей и одна плохая. Хорошие: в опубликованной статье указывается несколько проблем, в которых были совершены открытия; некоторые из них можно объяснить «на пальцах». Плохая: главную научную проблему и её ценность объяснить на пальцах сложно — вы же не думали, что всё так просто? Поэтому вот как мы поступим: сначала кратко и в общих чертах обсудим основную математическую задачу, прорыв в которой и является большим событием, а дальше рассмотрим более доступную (но менее впечатляющую), и уже с этим примером в руках будем разбираться в принципе работы алгоритма.
Карты, точки, три столпа: настольные игры и наука
В центре проблемы лежит малопопулярная игра Сет (или Трикс), по правилам слега напоминающая УНО! Всего в колоде 81 карта, и каждая из них характеризуется четвёркой параметров: тип фигуры на карте, её цвет, количество и текстура (тип закрашивания). Для каждого из параметров может быть 3 варианта. Например, одна, две или три фигуры. Или зеленый-синий-розовый, если речь про цвета. Поэтому карт столько: всего комбинаций 3*3*3*3.
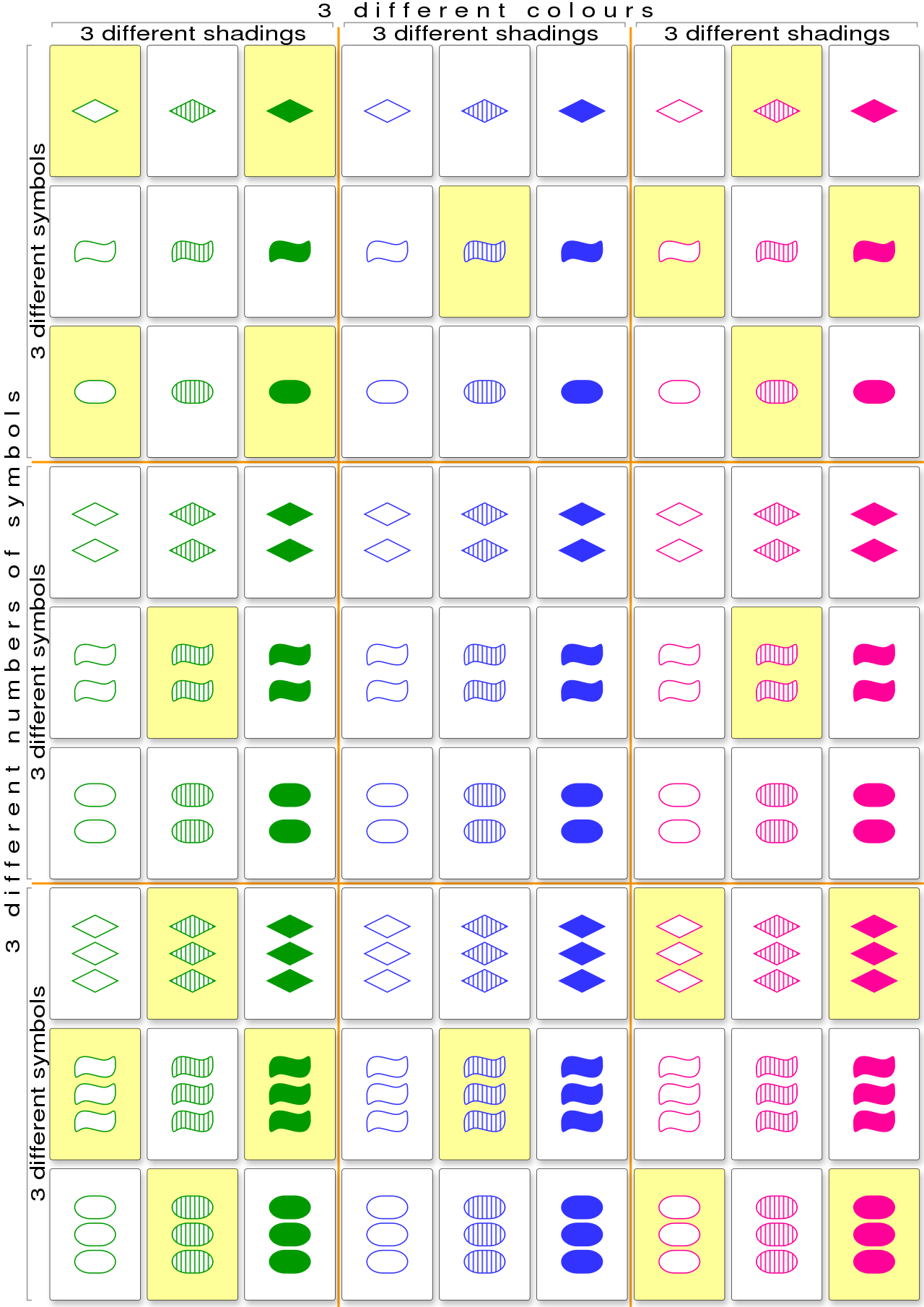
Ключевым в игре является понятие «множества» (собственно, set по-английски, отсюда и название), описывающее набор из трёх карт. Множество можно определить так: для каждого из четырех параметров (это цвет, количество, форма и текстура) все три карты должны отображать этот признак либо как а) все одинаковые, либо б) все разные. Звучит сложно, но при визуализации всё становится проще:
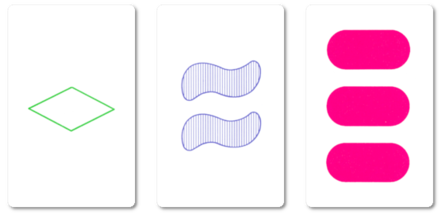
Ведущий постепенно выкладывает карты на стол, и игрок, заметивший сформированное множество, должен выкрикнуть «сет!». После этого он может забрать эти 3 карты себе (ведь в сете всегда 3 карты). Однако может так получиться, что сет долгое время не выпадает — и не потому, что игроки проворонили, а потому, что его действительно просто нет на столе. Тогда по правилам, если в игре оказывается 12 карт, то они убираются со стола; ведущий берёт три карты с верха колоды и выкладывает на пустой стол. Когда вся колода кончается, игра заканчивается, а игрок, набравший больше всего карт на руки, побеждает (не то что в УНО!)
Где-то в этот момент вы должны спросить себя «что за хрень? При чём тут открытия в математике и нейросети?». Дело в том, что математики часто фигнёй маются задаются вопросами, которые могут не иметь видимого смысла, и при этом имеют наглядные игрушечные демонстрации. Однако прелесть математики в том, что даже игры можно свести к формулам, в нашем случае — из теории множеств или афинной геометрии. Можно поставить карты колоды в соответствие точкам четырёхмерного пространства (потому что у нас 4 уникальных признака) над полем из трёх элементов (потому что карты три) . В таком случае сет соответствует трём коллинеарным точкам в этом пространстве — иными словами, трём точкам на одной прямой, и их сумма равна нулю.
Разбор двумерного случая для интересующихся
Если у нас всего два признака (например, цвет и форма объекта на карточке), то можно взять лист бумаги и нарисовать двумерную плоскость. У каждого признака всё еще ровно по три уникальных значения. Смена целочисленных значений по оси Ox может означать разные цвета, а по Oy — формы. Мы говорим про целые числа потому, что задача — дискретная: в её рамках не бывает 0.5 красного цвета или 0.3 треугольника.
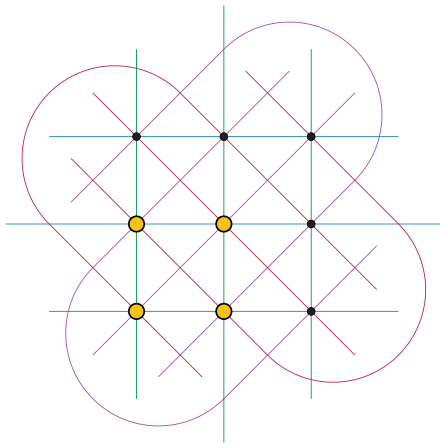
Тогда всего у нас в колоде 9 карт (в сетке 3*3, как и точек на графике выше). Для них можно выбрать лишь 4 точки так, чтобы никакие 3 не лежали на одной прямой. Если бы другая желтая точка была на продолжении одной из прямых (скажем, в верхнем правом углу, чтобы получилась диагональ), то точки бы схлопнулись в одну центральную, и их сумма равнялась нулю (при условии, что центр координат всегда в средней точке).
Теперь, когда все пережившие прошлый абзац почувствовали себя умнее, давайте определим набор карт, среди которых нет сета (или соответствующих им точек), и назовём его «cap set» (русского названия сходу не нашёл, Википедия предлагает «множество колпаков», но без указания источника). Это как раз те 12 карт, которые нужно будет убрать со стола, если все игроки затрудняются найти сет.
А вот почему 12? Почему не 10 или 15? И вообще можно ли посчитать, сколько максимум карт можно выложить на стол так, чтобы не было сета? Поздравляем, если вы задались таким вопросом — вы только что сформулировали задачу The Cap Set Problem. Для нашей игрушечной колоды ответ равняется 20, а число 12, видимо, выбрано потому, что людям очень сложно перебирать все комбинации в голове по ходу игры.

Но эту же задачу можно сформулировать в общей форме. Оказывается, на данный момент не известно формулы, которая по количеству уникальных признаков (вроде цвета или формы фигуры), разделяющих карты, будет вычислять размер cap set. Иными словами ответить на вопрос «сколько карт можно выложить на стол так, чтобы никто не кричал СЕТ!!! как угарелый?» невозможно. У нас есть лишь оценки верхней и нижней границ (формулы, которые указывают, в каких рамках лежит искомое значение), которые постепенно уточняются, а также посчитаны размеры максимально возможного cap set для количества признаков до 6 включительно. Почему не пошли дальше, хотя бы чисто по приколу? Ну, потому что это сложная вычислительная задача, где нужно сделать полный перебор всех комбинаций, число которых стремительно растёт. Пока не найдено решение в общем виде (та самая формула), считается, что без перебора проверить корректность ответа невозможно.
Для 8 признаков нужно будет перебрать всего лишь 3^1600 троек карт, что на порядки больше, чем количество атомов во Вселенной. Да что там, в игре Го, которая считалась невозможной для игры компьютером на уровне человека, длина числа валидных состояний доски — это число с 171 цифрой. А для нашей карточной игры при 8 признаках количество троек карт измеряется числом с 764 цифрами. Страшно?
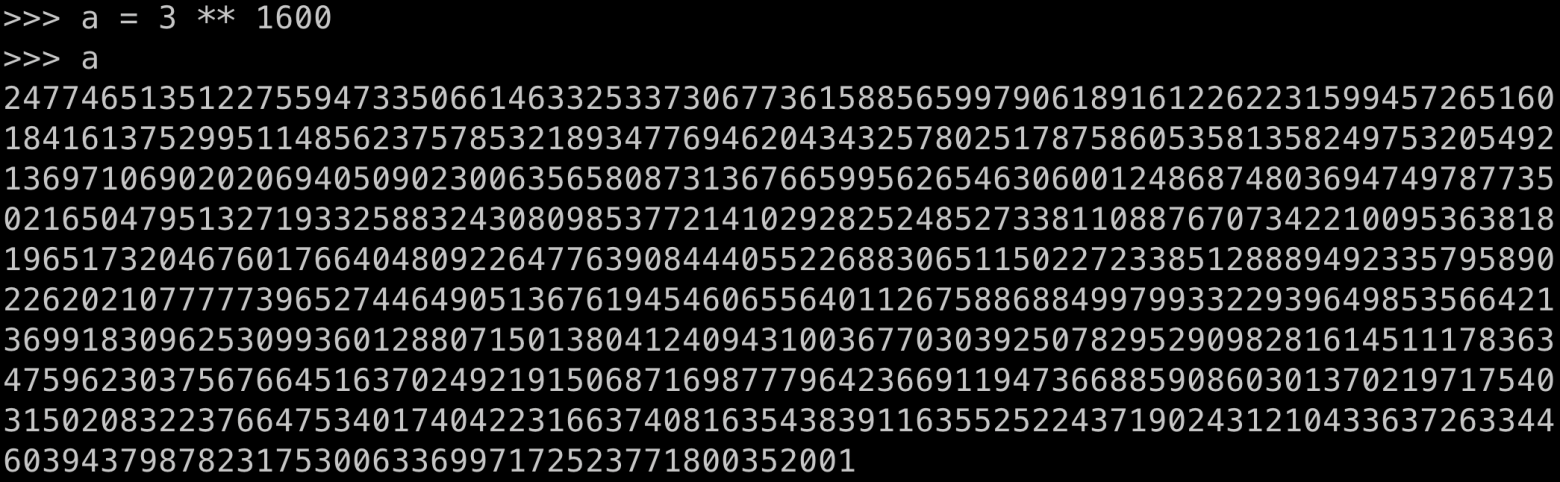
Так вот, именно для этой задачи языковая модель от Google и написала код, который...нет, не находит точное значение или формулу (то есть определяет истинную зависимость). Этот код лишь генерирует такие наборы, для которых очень легко проверить, что все правила соблюдены (то есть получен истинный cap set), и размер этого набора для 8 признаков больше, чем у любого другого, найденного человечеством с момента появления математической задачи.

Насколько мне удалось проверить — метод пока не запатентован, так что торопитесь!
Напомню, хоть всё может показаться игрушечным, какие-то карты, красные ромбики и зеленые овалы — это научная проблема, над которой билось множество исследователей, писались научные работы. А всё потому, что никогда не знаешь наперёд, где пригодится твой результат. Вот даже для этой проблемы, уточнение лишь верхней оценки на количество элементов в cap set немедленно привело к ряду других результатов в комбинаторике, например, приблизило к разгадке задачи о подсолнухе (карточки, подсолнухи, что дальше? Грибы? Их уже хватит...). Это подчеркивает, насколько методы, предложенные DeepMind и описываемые ниже, могут быть полезны в научно-исследовательской работе — пусть даже без видимого для обывателя эффекта.
Далее в тексте я буду по большей части игнорировать описанную выше проблему, так как жонглировать всеми терминами в абстрактной задаче сложно, но не забывайте, что речь идёт про реальные научные открытия. А теперь мы перейдем к...
Задача об упаковке в контейнеры
к описанию более простой задачи, понятной каждому: упаковка в котейнеры. Цель здесь — упаковать набор коробок разного размера в наименьшее количество контейнеров фиксированного размера. Подождите, не закрывайте статью — это реально прикладная задача, честно! И используется не только на складах! С минимальными изменениями решения этой задачи можно применять хоть на реальном производстве при резке материалов, хоть при планировании ресурсов и распределении задач на серверах для уменьшения трат — главное, что у вас есть что распределять и куда.
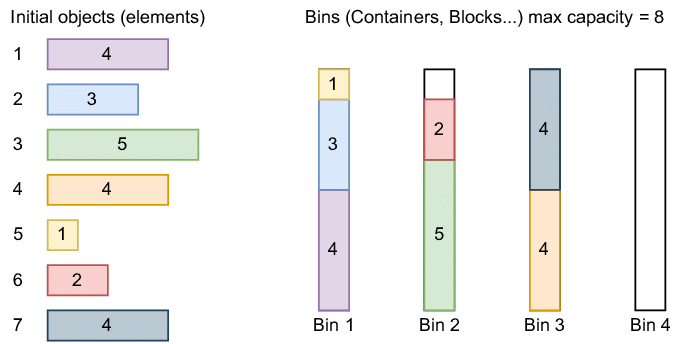
В такой задаче выбрать правильную стратегию заранее очень сложно. Математически доказано, что для гарантированно лучшего результата вам необходимо перебрать все возможные варианты (прямо как в задаче выше, The Cap Set Problem). Поэтому чаще всего люди соглашаются с достаточно хорошей стратегией, которая может и не является лучшей, но лишь слегка ей проигрывает. Зато работает быстро и почти везде!
Такие «наколеночные» стратегии часто называют эвристиками, и они базируются на опыте и экспертизе в рамках конкретной задачи. Придумать хорошую эвристику очень сложно, так как в голове нужно держать множество ситуаций разом.

Но одно дело заниматься распределением ресурсов (или раскладкой по контейнерам), когда вся информация о наполнении есть заранее, а другое — когда то и дело прилетают новые коробки, которые сразу надо «упаковать». Лучший пример тут — это выделение вычислительных ресурсов для задач на кластере, и на масштабах крупнейших корпораций вроде Google или Facebook даже 1-2% выигрыша — это десятки и сотни миллионов долларов экономии в год. Каждую минуту вам прилетают тысячи новых запросов, которые нужно выполнить, и вы можете ливо выделить новый пустой сервер, либо попытаться найти уже загруженный, но не настолько, чтобы новая задача (коробка) «не влезла». Google даже хвастался, что получилось применить нейросети для оптимизации хранилищ, и это экономит 19% пространства на дисках — что опять же приносит выгоду в десятки миллионов.

Формально, задача выглядит так: на каждом шаге нам приходит информация о новой коробке (её размере, для простоты это будет одно число), и мы можем либо взять новый пустой контейнер, чтобы загрузить коробку в него, либо выбрать один из частично заполненных контейнеров и закинуть туда сверху. Когда коробки закончатся — мы считаем, сколько всего контейнеров потребовалось. Логично, что хочется задействовать как можно меньше хранилищ — а для этого нужно достичь наиболее плотной упаковки, с меньшим количеством пустот.
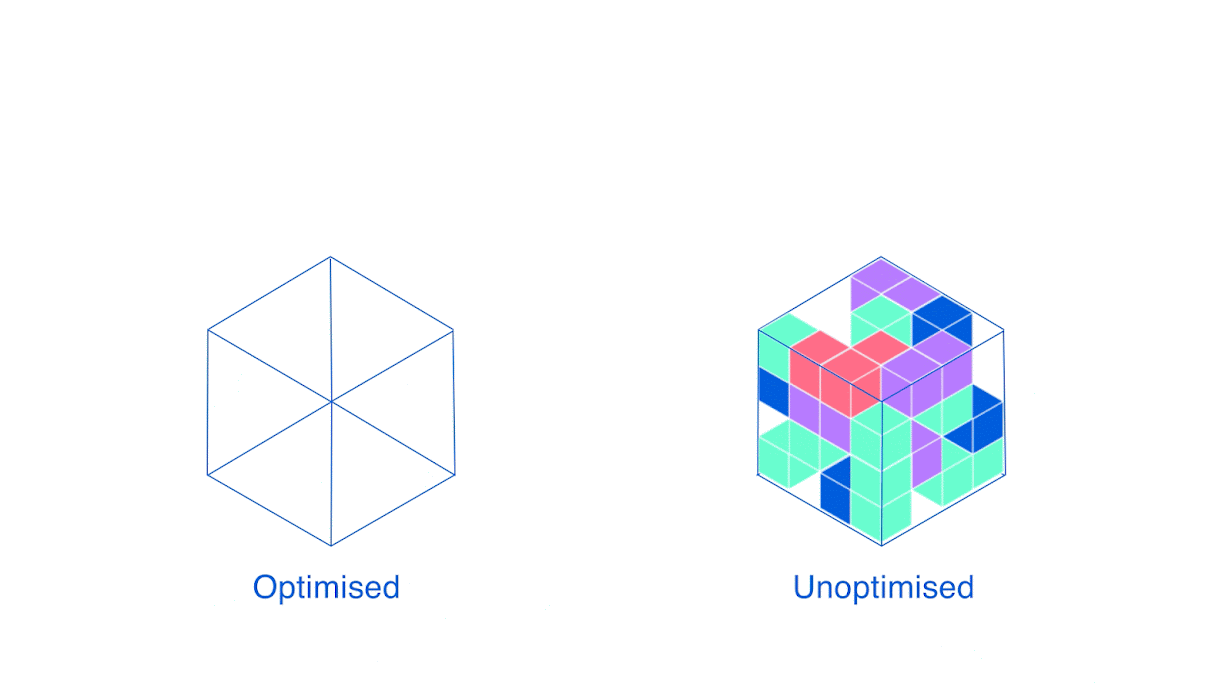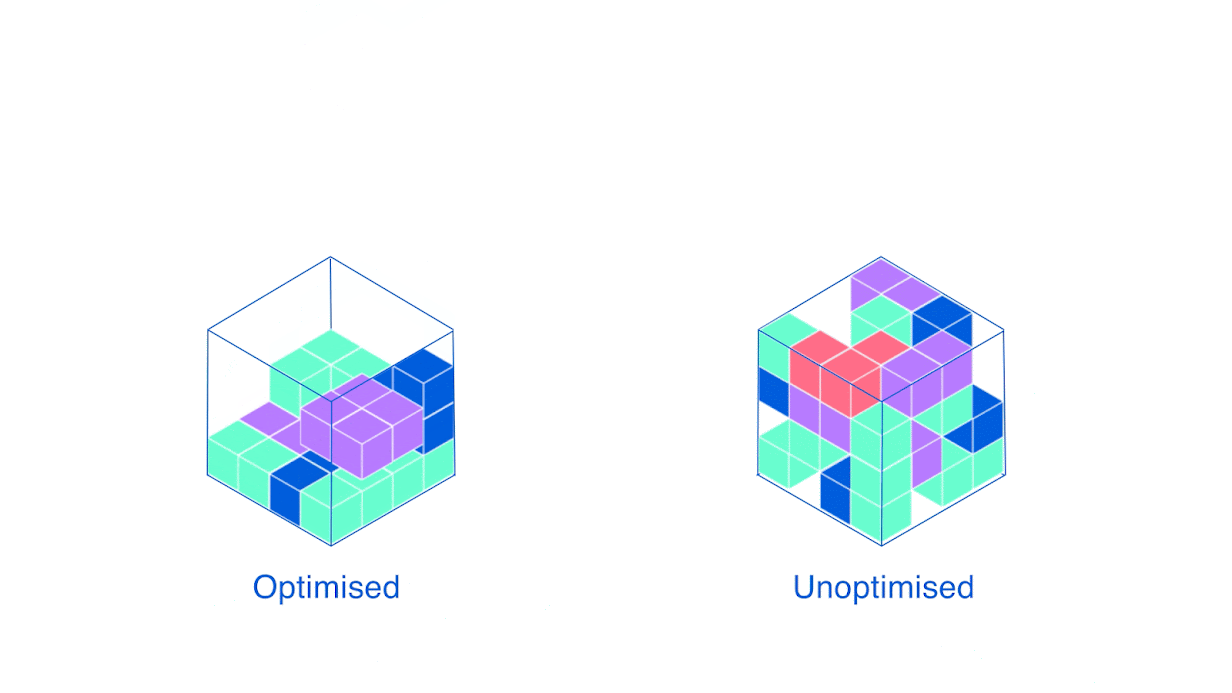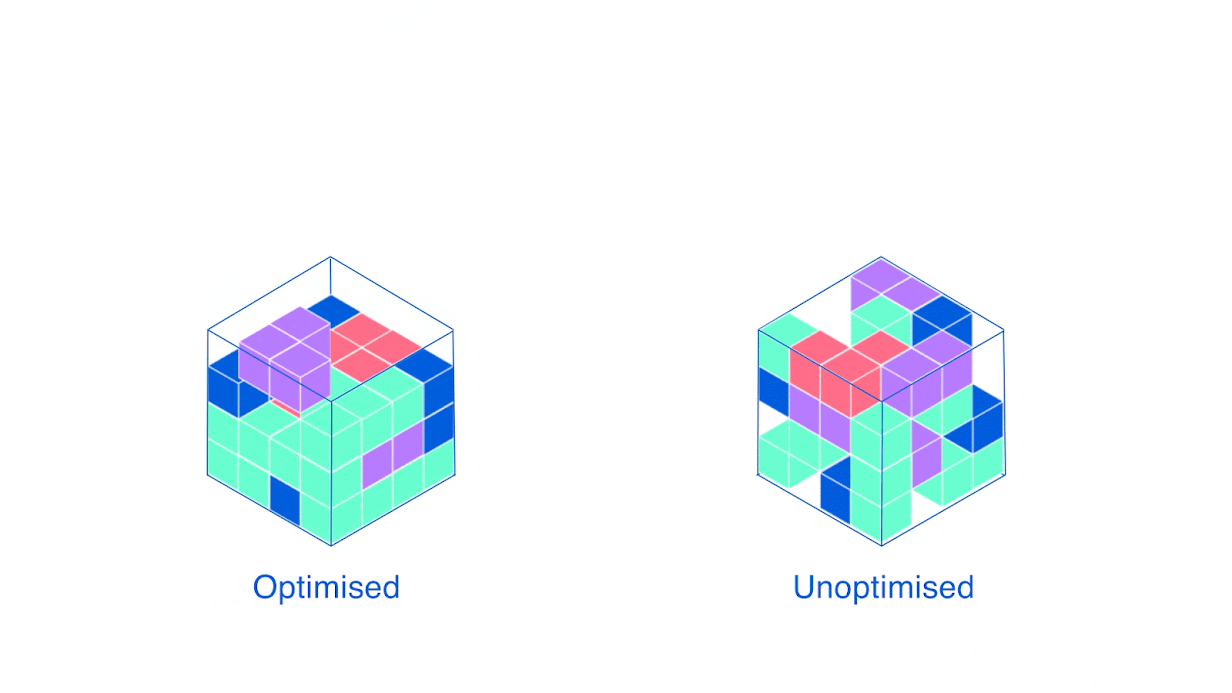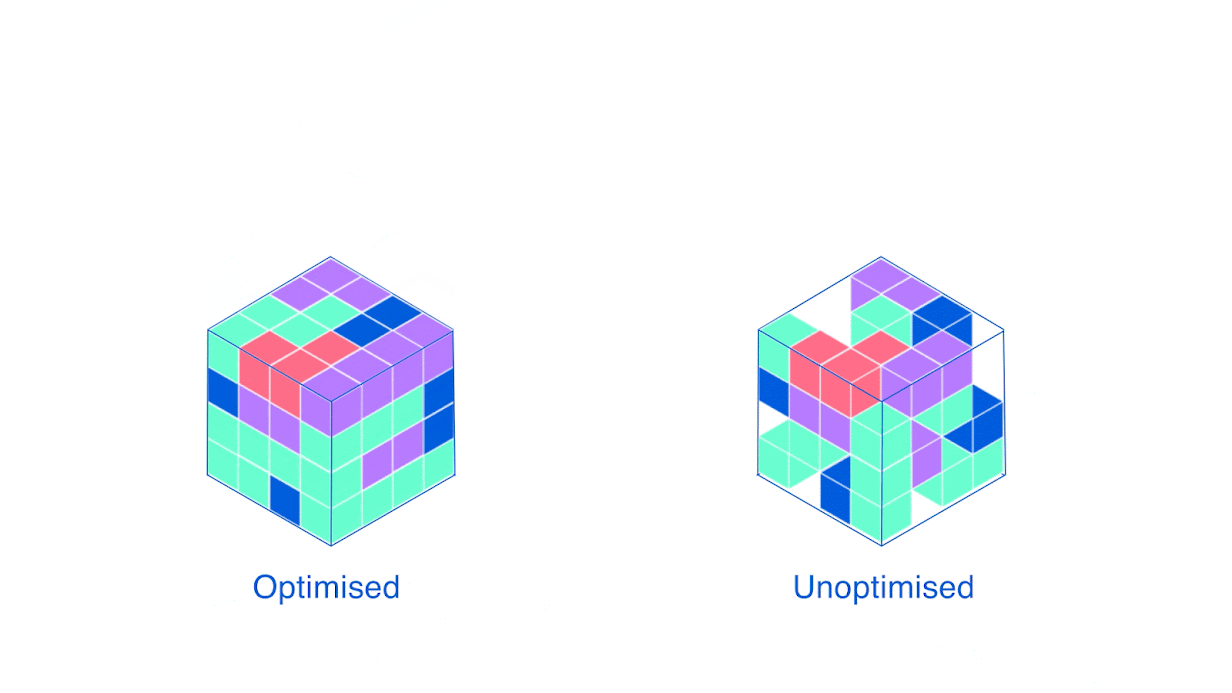
Хорошая новость об эвристиках в том, что их очень легко сформулировать словами — поэтому я вам о них расскажу! Широко распространёнными приёмами для вышеупомянутой задачи являются «первое соответствие» (закидываем коробку в первый с начала контейнер, куда она вмещается) и «наилучшее соответствие» (выбираем тот, где останется меньше всего места). Звучит логично, да и на практике в среднем работает хорошо. Но можно ли лучше, и если да, то как?
Пятиминутка про LLM'ки
Правильно сформулировать проблему — это уже полдела. Давайте же посмотрим на метод, предложенный исследователями DeepMind. В сердце системы лежит LLM, большая языковая модель Codey. Если вы не до конца понимаете принцип работы LLM или хотели бы более глубоко разобраться в процессе обучения — рекомендуем прочитать две предыдущие статьи от меня:
Как работает ChatGPT: объясняем на простом русском эволюцию языковых моделей с T9 до чуда;
GPT-4: Чему научилась новая нейросеть, и почему это немного жутковато.
Вкратце вспомним, что это за зверь. LLM — нейронная сеть, обученная предсказывать следующее слово (или токен, то есть частичку слова) на огромнейшем наборе текстов со всего интернета. Такую сеть можно «промптить» (писать промпт), то есть человеческим языком объяснять, что нужно делать. Также как и кожаным мешкам, ей можно давать примеры — а она на лету уловит, что вы от неё просите. Это не работает идеально для всех задач, и часто модель может запутаться или ошибиться. Поэтому самые известные LLM вроде ChatGPT и называют ассистентами — они не делают всю работу за вас, а лишь пытаются помочь. Чтобы осуществить свою функцию, они учитывают контекст диалога — то есть некоторую часть предшествующей беседы.
Важная архитектурная деталь модели заключается в том, что она — вероятностная. Любой ответ от неё не гарантирован, и при повторном запросе можно получить другой результат. Неправильные части в нём могут стать корректными — и наоборот. Однако любой ответ старается быть приближенным к естественному человеческому (ведь она обучена на наших текстах в интернете), а также следует принципам максимизации полезности и точности.
Снятся ли LLM'кам обезьяны?
Тут можно вспомнить бородатый парадокс с интересным названием: Теорема о бесконечных обезьянах. Она утверждает, что абстрактная обезьяна, ударяя случайным образом по клавиатуре в течение неограниченно долгого времени, рано или поздно напечатает любой наперёд заданный текст — даже «Войну и мир». В некотором смысле обезъяна тоже вероятностная модель, но очень простая: она не учитывает контекст, каждая следующая буква почти наверняка не зависит от предыдущей, а вероятность удара по любой клавише примерно одинаковая. Современные LLM всё же умнее, они порождают текст, зачастую неотличимый от написанного человеком.

Выходит, если в этой истории заменить обезъяну на ChatGPT и запросить текст решения научной проблемы — это сработает? Ну, за бесконечное время — в теории да; жаль, что это непозволительная для нас роскошь. К тому же, важным ограничением обоих подходов (обезьяннего и нейросетевого) является необходимость наличия валидатора. Это такой механизм, который из триллионов написанных текстов сможет выявить правильный. Тогда поочередёно применяя его к каждой странице бессмыслицы в какой-то момент мы сможем выцепить результат.
Если честно, с первого взгляда не звучит как что-то умное — ведь для такого валидатора как будто бы нужен оригинал, с которым будет идти сравнение. Однако в очень широком классе задач процесс валидации зачастую быстрее процесса генерации (или порождения) сущности. Вообще, на этом основана вся криптография, которая позволяет вам спать спокойно и не переживать, что кто-то украдёт все биткоины с крипто-кошелька. Проверить валидность пароля или ключа можно моментально, а вот подбирать его даже на суперкомпьютере нужно тысячелетиями.
Этот принцип верен для разобранных нами задач — можно легко посчитать количество контейнеров, которые требуются для упаковки коробок одной эвристикой и другой. Мы просто запускаём программу на компьютере, ждём пару секунд — и видим результат, который или лучше, или нет. При этом нам не нужно образцовое решение: зачастую достаточно показать результат не хуже, чем текущий лучший. Вспомните задачу с определением наибольшего множества карточек на столе, в котором нет сета (cap set). Если проверка проходит, то мы сразу же знаем размер набора, а затем сравниваем его с предыдущим.
Чтобы эта концепция работала в реальном мире, важно уменьшить количество времени на перебор вариантов с бесконечного до приземлённого. Мы заведомо не генерируем мусор, не связанный с задачей, и к тому же можем использовать историю, анализировать её и корректировать стратегию «печатания». Как было указано выше, в этом прелесть LLM — они внимательны к контексту.
Начинаем генерацию
Осталось понять, что именно генерировать. Давайте в рамках описанных задач мы будем писать Python-код, который воспроизводит решение, а не непосредственно финальный ответ. У этого подхода множество плюсов: во-первых, хорошо написанный код гораздо более понятен человеку, его можно прочитать и разобрать. Во-вторых, код программы обычно куда короче, чем полный ответ (для одной из проблем ответом служили тысячи чисел — а код умещался в 15 строк). В-третьих, код может быть гибким и хорошо обобщаться: есть шанс, что он работает не на одной конкретной проблеме, а на целом множестве, в то время как ответ, он один. Не беспокойтесь, если что-то не ясно — всё будет продемонстрировано ниже.
Вернёмся к проблеме оптимальной упаковки. Наша задача — написать эвристику, которая получает на вход размер текущей коробки (помните, что мы не видим всех коробок за раз, они приходят поочерёдно) и состояние контейнеров — сколько свободного места в них осталось. В данном случае логичным кажется следующий подход: для каждого контейнера оценивается его приоритет, а затем коробка попадает в то хранилище, у которого наивысшая оценка. Здесь не нужно генерировать весь код решения — какую-то часть можно написать вручную, а нейронке делегировать исключительно функцию оценки. Мы как бы «изолируем» маленькую часть логики, которую важно улучшить, не трогая всё остальное. Это позволяет включить в решение некоторое знание, которое имеется у нас, людей, без необходимости модели его переоткрывать. Ну и объем поисков сокращается существенно!

На самой первой итерации модели подаётся простое решение и описание проблемы — и та генерирует несколько как можно более разнообразных решений. Назовём их изначальной популяцией. Провалидируем, что все программы запускаются и выдают ответ в правильном формате — если это не верно, то такое решение удаляется. А после применим ловкий трюк и сформируем промпт (запрос к модели) следующим образом: вот нулевая версия кода, вот первая, напиши вторую.

Поскольку LLM обучена быть полезной и выполнять инструкции, то...самым логичным вариантом продолжения генерации является какая-то программа, которая и решает проблему, и чуть-чуть лучше. Примерно в этот момент обезьяна начинает бить по клавиатуре, и в результате получается новая программа. Мы можем тут же её провалидировать: она либо не работает (и мы её выбрасываем), либо работает хуже исходных (никакого улучшения нет), либо...улучшает результат. Последний случай самый желанный и при этом самый редкий.
Сделайте миллион итераций, каждый раз выбирая одни из самых успешных решений (ведь мы их сразу же оцениваем) — и получите научный прорыв. Единственная проблема, которая может возникнуть на пути к успеху — это однородность генераций: весь код может делать по сути одни и те же операции, не вносить никакой новизны относительно существующей «базы решений», и заходить в тупик. Для борьбы с этим авторы используют островной эволюционный метод: разные группы программ как бы «живут» в отдельных группах (на островах), а раз в несколько часов половину худших островов «смывает». Плохость здесь определяется оценкой самого лучшего решения на острове. После наводнения, острова населяются «выжившими», предпочитая в первую очередь более успешные решения. Колесо Сансары заходит на новый круг.

Более того, внутри островов также есть кластера (назовём их «племенами»), которые автоматически выделяются на основе структур программ (методов, которыми решается задача — используя AST-парсинг). И несмотря на то, что нулевая и первая версии для промпта в LLM всегда выбираются с одного острова, оказывается выгоднее скрещивать племена между собой, чтобы получать более креативные и разнообразные решения.
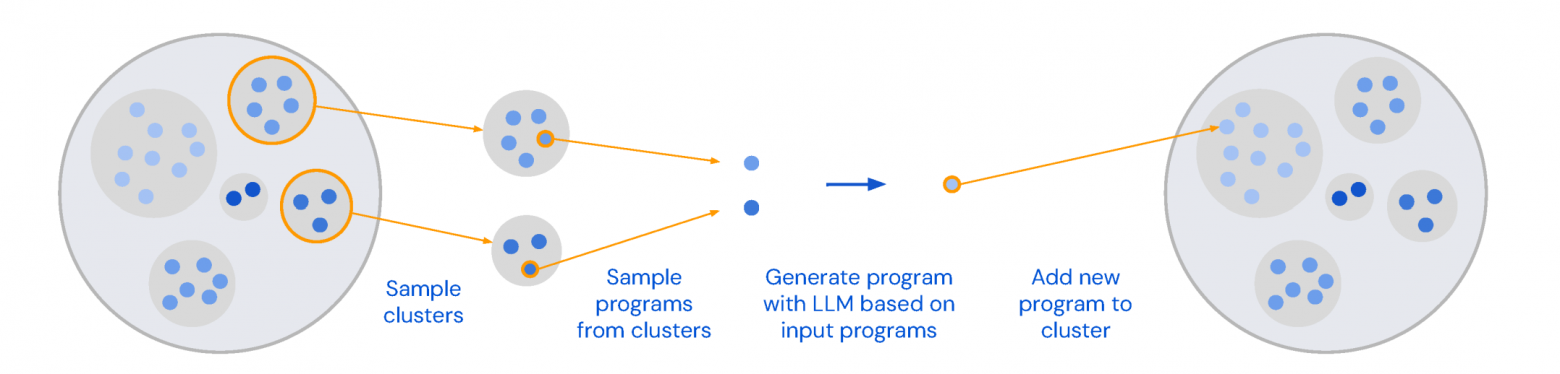
Таким образом, разные группы перспективных решений сосуществуют и могут пересекаться. Это очень похоже на колонии бактерий, которые могут мутировать независимо друг от друга, и иногда смешиваться. По ходу «развития» колонии программ происходит множество изменений (можно окрестить их мутациями), а также слияния идей из разных групп решений — поэтому алгоритм и называется эволюционным: его идеи были подсмотрены у самой природы. Но он не уникален, есть целое семейство алгоритмов, придуманное людьми по схожей аналогии — просто тут решили остановиться на идее островов.
И вот если оставить этот цикл жизни крутиться на пару суток, дать смениться паре миллионов поколений — лучшая из оставшихся программа будет решать исходную задачу лучше мясных учёных (наверное). Но это не точно. Однако именно таким способом были получены ответы, названные «прорывными находками в области математики». Их действительно не существовало, они нигде не были записаны или озвучены любым учёным. Это на 100% новая для человечества полезная информация, новое научное знание. Большая Языковая Модель генерировала-генерировала да выгенерировала. Сравнение результатов работы простой эвристики и найденной нейронкой можно увидеть ниже — в конечном итоге используется на один контейнер меньше, и это победа!
И этот метод, названный FunSearch (Fun не потому что смешно, а потому что Function Search, поиск функции) достаточно универсален, хоть и имеет свои ограничения:
Должна быть доступна легковесная быстрая функция валидации решения (проверяем, что программа имеет смысл);
Эта функция должна быть не бинарной, а численной, чтобы можно было сравнивать решения и оценивать улучшения. В случае задачи упаковки эта функция — количество неиспользуемого свободного места (или количество контейнеров);
Решение можно представить в виде кода или текста (самое слабое ограничение, так как языком можно выразить практически всё).
То есть таким методом без внесения изменений не получится взять и заменить учёных, обрисовывая лишь общую задачу в духе «а вот тебе теорема, реши её»: не выполняются пункты 1 и 2. Нельзя взять два неправильных доказательства, за секунду их проверить и оценить, какое ближе к истине (ведь мы не знаем ответ). Но даже в этих рамках существует большое количество полезных задач, для которых будет экономически целесообразно гонять нейронку миллионы раз.
Сработало ли?
Но вернёмся к коробкам и контейнерам. Несмотря на то, что нейросети считаются чёрными ящиками, которые мы не понимаем, порождённый ими код оказалось легко разобрать и интерпретировать. Была найдена такая эвристика: вместо того, чтобы упаковывать коробки в контейнеры с наименьшей оставшейся вместимостью, решение распределяет их только в том случае, если после этого почти не остаётся пустого места; в противном случае коробка обычно помещается в другой контейнер, чтобы везде осталось побольше пространства. Эта стратегия позволяет избежать небольших зазоров в контейнерах, которые скорее всего ничем бы и не заполнились. Звучит легко, и может быть где-нибудь умный инженер такое и придумал (наверняка в тетрис много наиграл), но вот специалисты из Google приятно удивились.
К тому же, найденная эвристика обобщалась — её применили к таким же задачам со слегка изменёнными условиями (другие пропорции размеров коробок и контейнеров, разное количество коробок), и всё работало как часы. Чем больше коробок приходило на вход, тем ближе решение приходилось к оптимальному (как если бы мы заранее знали все коробки, что нам нужно распихать — напомним, что мы их видим по одной, без заглядывания в будущее, и это усложнение). То есть даже перезапуск FunSearch не понадобился, одна программа (одно решение) применялось для нескольких вариаций одной задачи.
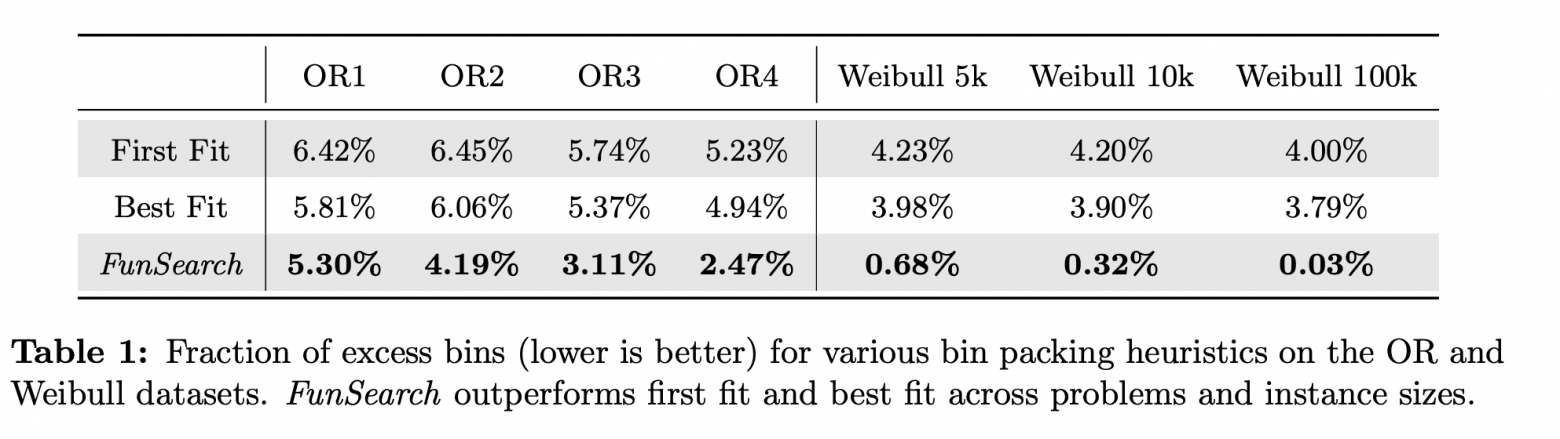
OR1 - OR4 это наборы задач со слегка меняющимися условиями. Несмотря на то, что модель при обучении видела лишь примеры из OR1, на всех остальных условиях решение всё еще лучше популярных эвристик.
И вот эта возможность прочитать решение — это очень важный пункт. Как мы уже написали, в статье помимо двух разобранных задач были и другие. Для одной из них во время анализа лучшего предложенного решения (которое само по себе уже превосходило разработанные человеком) выяснилось, что присутствует некоторая симметрия в сгенерированном ответе. Один из привлечённых учёных придумал, как это можно эксплуатировать, FunSearch получил уточнённые инструкции (с помощью ограничений — помните, что мы управляем тем, что именно оптимизируется), и новое решение оказалось ещё лучше — настолько, что про него написали: «это самое большое уточнение оценки нижней границы за последние 20 лет исследования проблемы».

«Решения, созданные FunSearch, концептуально гораздо богаче, чем просто наборы чисел. Когда я изучаю их, я что-то узнаю» — сказал Джордан Элленберг, привлечённый профессор математики. «Что меня волнует больше всего, так это новые способы взаимодействия человека и машины», — добавил он, «Я не смотрю на это как на замену людям-математикам, это мультипликатор их силы». What a time to be alive!
Но вернёмся с небес на землю и прагматично поговорим про деньги. Сколько вообще стоит запуск такой системы на миллионы генераций? Исследователи из Google проводили эксперименты с не самой большой и даже не самой современной LLM — они использовали Codey, основанную на PaLM 2 (нейросеть от Google предыдущего поколения, вышла весной 2023го; в декабре была представлена улучшенная Gemini). Возьмём за ориентир цену на использование ChatGPT версии 3.5 с ценой генерации $0.001-0.002 за тысячу токенов (~750 слов). По грубой прикидке, если взять с запасом, то в промпте содержится 2 программы на 1500 токенов, и ещё 750 мы получаем на выходе. Цена за 2.5 миллиона итераций составит $7500, и ещё сколько-то нужно потратить на серверы для запуска и оценки генерируемых решений (не больше $500).
Напомню, что эффект от оптимизации некоторых эвристик на масштабе датацентров Google составит десятки миллионов долларов в год, а научный прорыв с продвижением к заветному доказательству и вовсе может стать значимым событием в жизни учёных. Готовы ли вы вбухать 10 тысяч долларов? А сто? Миллион? Готовы ли будут корпорации заплатить 3 миллиарда долларов за рецепт лекарства от рака (если технология позволит находить и такие решения в виде исследовательских статей)? Как скоро нейросеть включат в соавторы работы, которая получит престижную награду вроде Нобелевской премии?
А что дальше? — Вместо заключения
Не поймите неправильно, показанные здесь открытия — не самые крупные в мире математики. Весь мир завтра не перевернётся. Это лишь следующая ступень на длинной лестнице развития технологии. Но мы шагаем всё дальше и дальше, а наши методы становятся более общими. По сути, такая идея перебора и оценки тысяч и тысяч плохих вариантов в попытках найти бриллиант, была давно — с её помощью компьютер обыграл человека в шахматы, она же лежит в основе AlphaGo — системы, сенсационно обыгравшей самого сильного игрока в Го (и тоже разработана DeepMind). Потом эти методы были применены для сжатия видео на YouTube на дополнительные 4% (помните про десятки миллонов долларов?), для оптимизации низкоуровневых процессорных команд (на которые больше 30 лет смотрели лучшие инженеры). Но во всех этих случаях задача была определена очень чётко, и несмотря на общую схожесть методов требовалось значимое количество ручной работы для их адаптации.
Сейчас система FunSearch может «искать» потенциально любую программу для решения задачи с условием упомянутых ограничений. Надеемся, что после прочтения этой статьи стало ясно, что ошибки нейросетей — это не баг, это фича. Ошибки не так страшны, правильный ответ скорее всего рано или поздно найдется — покуда мы можем валидировать и оценивать генерируемый текст. Томас Эдисон провёл несколько тысяч экспериментов в попытках создать нить накала для лампочки. «Я нашёл 2000 неправильных способов — осталось найти лишь один, верный» — говорил он.

Вот, к примеру, система для решения олимпиадных задач по программированию AlphaCode 1 (всё от тех же DeepMind) при генерации одного миллиона решений (и самостоятельной оценкой) справлялась лишь с 24% проблем (серая линия на графике). В её основе как раз лежит модель, аналогичная упомянутой Codey на основе PaLM 2. А синяя линия — качество новой AlphaCode 2 на основе Gemini (самая свежая и лучшая LLM Google). Заметьте, что при генерации всего лишь сотни (вместо миллиона!) решений она достигает того же уровня, а с миллионом попыток и вовсе достигает 46%. Грубо говоря модель стала в 10'000 раз эффективнее. Так что ждём обновления FunSearch с AlphaCode 2 под капотом, и кто знает, чего она там нарешает...

Лучшие умы бьются над тем, чтобы улучшить подход, аналогичный FunSearch — OpenAI вообще планирует создать автономного учёного в течение 4 лет (это правда. За счёт этого они хотят существенно увеличить штат, ведь не будет проблем с наймом — запустил нейронку и всё). У LLM будут развиваться навыки рефлексии, понимания, размышления — что позволит за то же количество попыток (читай денег) достигать ещё лучших результатов. Вообще ускорение научного прогресса — это невероятно важная штука, и даже если AI не войдет в нашу повседневную жизнь, то повлияет на мир вокруг. В заключение предлагаю послушать двухминутный отрывок с видением Сэма Альтмана и Ильи Суцкевера, заправляющих OpenAI (русские субтитры доступны; если таймкод не рабоатет, то смотреть с 16:38).
Мы летим в будущее, господа, и это будущее прекрасно!
Спасибо, что дочитали до конца! Обязательно оставляйте комментарии — постараюсь ответить всем. Лучший способ отблагодарить за статью — и увеличить свою осведомлённость об AI — это подписаться на мой телеграм-канал «Сиолошная». Там я делаю заметки почти каждый день и стараюсь доступным языком объяснить, что вообще происходит.







