Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!

Привет, Хабр!
Новогодние праздники — отличное время, чтобы отдохнуть от IT использовать профессиональные навыки в любимом хобби. Ковыряясь на сайте рейтинга спортивного ЧГК, я обнаружил отличный API, позволяющий получить данные о всех играх всех турниров. Так у меня появилась идея построить граф сообщества знатоков и проверить теорию шести рукопожатий на географически разбросанном и строго оффлайновом коммьюнити. Под катом картинки графов и бесполезная статистика.
Для начала краткий ликбез, что такое спортивное ЧГК.

Уверен, что с телевизионной версией «Что? Где? Когда?» с волчком и письмами телезрительниц читатель знаком. Спортивное ЧГК — это расширение телевизионного формата, позволяющее играть нескольким командам одновременно.
В кафе, доме молодёжи, актовом зале университета собираются несколько команд численностью до шести человек. Ведущий зачитывает вопросы, на размышление даётся по одной минуте. По окончании минуты команда записывает ответ на игровой бланк и поднимает вверх. Специально обученные люди, именуемые ласточками, собирают бумажки. Обычно за игру читается 36 вопросов, разделённые в три тура. Кто больше всех ответил, тот и молодец.
Существует много турниров по ЧГК, есть даже чемпионат Европы и мира, любопытных отсылаю к авторитетнейшему источнику информации. А примеры вопросов можно найти тут.
Получение данных
Будем считать, что игроки знакомы друг с другом, если они сыграли хотя бы раз за одним игровым столом. Благодаря хорошему API скачивание данных о всех турнирах и всех командах не представляет проблем.
Под спойлерами не используется даже Beautiful Soup, только requests. Jupyter notebook со всем исходным кодом будет в конце статьи.
url = 'https://rating.chgk.info/api/tournaments.json/?page={}'
df = pd.DataFrame(columns=['name', 'start'])
for i in range(1, 7):
data = requests.get(url.format(i)).json()
for item in data["items"]:
df.loc[item["idtournament"]] = (item["name"], item["date_start"])
df.to_csv('tournaments.csv')Осталось скачать игровые составы всех турниров и запомнить все знакомства. Первоначально я планировал хранить факты совместной игры в DataFrame, однако скорость добавления новых записей оказалось удручающей. Поэтому заведём set из tuple'ов (id1, id2), где id1, id2 — идентификаторы игроков, знакомых между собой. Заодно избавимся от дубликатов.
df = pd.read_csv('tournaments.csv').set_index('Unnamed: 0')
url = 'https://rating.chgk.info/api/tournaments/{}/recaps.json'
links = set()
for id in df.index:
teams = requests.get(url.format(id)).json()
for team in teams:
t = team["recaps"]
for i in range(len(t)):
for j in range(i + 1, len(t)):
first = int(t[i]["idplayer"])
second = int(t[j]["idplayer"])
if first < second:
links.add((first, second))
else:
links.add((second, first))
# побережём сайт рейтинга
sleep(1)
clear_output(wait=True)
display('Current tournament: ' + str(df.index.get_loc(id) + 1) + '/' + str(len(df)))
display('Links total: ' + str(len(links)))Получение графа и исследование компонент связности
Итак, с подготовкой данных покончено, пора строить граф! Для этого воспользуемся библиотекой networkx, возможностей которой вполне достаточно для нашего кластера.
players = itertools.chain(*links)
G = nx.Graph()
G.add_nodes_from(players)
for t in links:
G.add_edge(*t)
print(nx.info(G))Сейчас в сообществе ЧГК около двухсот тысяч человек, а в среднем знаток за карьеру играл с 12 людьми:
Number of nodes: 198145
Number of edges: 1206076
Average degree: 12.1737Пришло время узнать, сколько компонент связности есть в графе знакомств. В networkx есть замечательная функция connected_components, которая делает как раз то, что нужно:
clusters_l = [len(c) for c in sorted(nx.connected_components(G), key=len, reverse=True)]
print(clusters_l[:20])Почти три четверти игроков состоят в одной компоненте связности, остальные разбиты по очень маленьким подграфам. Всего их более восьми тысяч.
[145922, 153, 124, 74, 72, 56, 50, 47, 42, 40, 39, 39, 38, 38, 37, 36, 36, 36, 36, 35]Даже в логарифмическом масштабе доминирование главной компоненты выглядит внушительно. По оси Х — номер компоненты от большей к меньшей, по оси Y — её размер (ось логарифмическая).

Чем же вызвано такое неравномерное распределение людей по связным компонентам? На мой взгляд, дело в следующем:
- небольшая группа людей первый раз приходит на игру и тем самым образует небольшой кластер на 4-6 человек;
- если в городе уже есть большое коммьюнити, такой кластер очень быстро сольётся с главным — достаточно всего одному человеку сыграть за команду из основного кластера;
- если же в городе ЧГК только появилось, кластер проживёт дольше, т.к. сыграть за команду из основного кластера сложнее.
Процесс напоминает образование дождевых капель в облаках: большая капля притягивает маленькие и быстро растёт.
Прежде чем заняться основном компонентой, давайте посмотрим на компоненты на первом-девятом месте (считаю основную компоненту нулевой). Проверим гипотезу, что люди в этих компонентах из одного города. У знатока нет привязки к городу (что логично в нашем современном мире). Однако можно посмотреть на порт приписки команды, за которую он играл в последний раз
for i in range(1, 10):
_g = list(sorted(nx.connected_components(G), key=len, reverse=True)[i])
s = pd.Series()
p_url = 'https://rating.chgk.info/api/players/{}/tournaments.json'
t_url = 'https://rating.chgk.info/api/teams/{}.json'
for player in _g:
data = requests.get(p_url.format(player)).json()
for item in data:
team_id = data[item]["tournaments"][0]["idteam"]
data = requests.get(t_url.format(team_id)).json()
town = data[0]["town"]
s.at[len(s)] = town
print('Кластер #{}'.format(i))
print(s.value_counts())Итоговая табличка:
| № компоненты связности | Размер | Города |
|---|---|---|
| 1 | 153 | Керчь |
| 2 | 124 | 110 — Усть-Илимск, 12 — Владивосток, 2 — Иркутск |
| 3 | 74 | Тамбов — 72, Люксембург — 2 |
| 4 | 72 | Лесной |
| 5 | 56 | Ейск |
| 6 | 50 | Бишкек |
| 7 | 47 | Горно-Алтайск |
| 8 | 42 | Житомир — 37, Глазов — 5 |
| 9 | 40 | Горно-Алтайск — 31, Москва — 9 |
Да, малые кластеры почти полностью из одного города. Прошу обратить внимание на компоненту из семидесяти двух тамбовчан, которая связана с Люксембургом. На седьмом и девятом месте компоненты из Горно-Алтайска, которые почему-то не связаны между собой. Мне охотно представляется борьба двух ЧГК-ашных кланов, наподобие Монтекки и Капулетти, которые бьются за контроль над городом.
Предположу, что в ближайшем будущем эти компоненты вольются в состав основной, но будут продолжать бороться.
Основная компонента связности
Итак, мы подобрались к основной компоненте. Получим нужный подграф и посмотрим на его статистику:
subgraph_v = list(sorted(nx.connected_components(G), key=len, reverse=True)[0])
subgraph = G.subgraph(subgraph_v)
print(nx.info(subgraph))Среднее число связей получилось больше.
Number of nodes: 145922
Number of edges: 1070504
Average degree: 14.6723А каково максимальное количество связей одного игрока?
for t in sorted(G.degree, key=lambda x: x[1], reverse=True)[:10]:
print('Игрок {} играл с {} игроками'.format(t[0], t[1]))Игрок 42511 играл с 818 игроками
Игрок 15051 играл с 798 игроками
Игрок 29800 играл с 678 игроками
Игрок 23020 играл с 666 игроками
Игрок 16581 играл с 662 игроками
Игрок 5328 играл с 657 игроками
Игрок 29887 играл с 651 игроками
Игрок 15811 играл с 645 игроками
Игрок 30352 играл с 605 игроками
Игрок 1055 играл с 602 игрокамиПризнаться, я немного шокирован полученными цифрами. Если каждый раз играть с новой командой, то понадобится 818/5 ≈ 164 игры, чтобы выйти на первое место. Невероятно.
Первых двух знатоков в этом рейтинге мы запомним и будем использовать их коммуникативные навыки далее.
Давайте оценим, сколько ближайших знакомств у среднего знатока:
_count = 50
values = nx.degree_histogram(subgraph)
plt.figure(figsize=(16, 8), dpi=80)
plt.plot(range(_count),values[:_count],'ro-') # in-degree
plt.xlabel('Число знакомств', fontsize=18)
plt.xticks(range(0,_count, 5))
plt.ylabel('Число игроков', fontsize=18)
plt.title('Число знакомств', fontsize=22)
plt.show()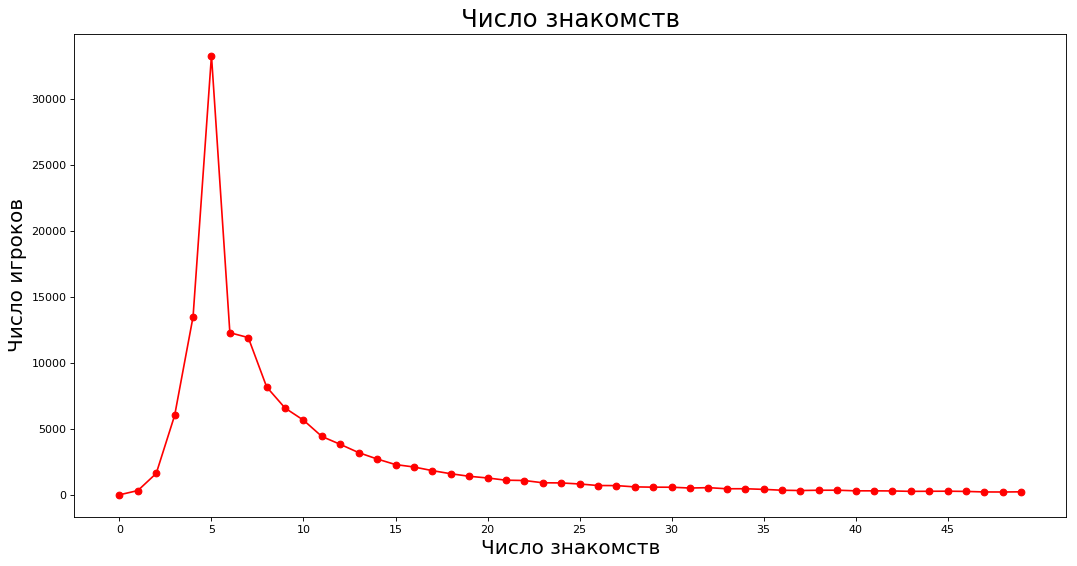
По оси X — число ближайших знакомств, по оси Y — количество знатоков, которое имеет соответствующее число знакомств. Например, по пять знакомств имеют приблизительно 40 000 знатоков.
Отметим, что мода — 5 знакомств (забавно, что за столом может находиться до шести человек). При этом среднее арифметическое числа знакомств — 14.67, а медиана — 7. Дело в том, что господа из рейтинга выше сильно завышают среднее. Если сто человек не играют в ЧГК, а один имеет 800 знакомств, то в среднем они играют в ЧГК.
Расстояния до игроков
Т.к. считать диаметр такого графа немного сложно, поступим проще: возьмём список из нескольких игроков и найдём максимальное из кратчайших расстояний от них до других знатоков. В качестве этих игроков я взял нескольких известных знатоков, себя, случайного игрока и двух знатоков с наибольшим числом знакомств (см. рейтинг выше). Вот что получилось:
famous_players = {9808: 'Александр Друзь',
5195: 'Анатолий Вассерман',
25882: 'Максим Поташев',
29333: 'Михаил Скипский',
118622: 'Михаил Атепаев',
42511: 'Николай Некрылов',
15051: 'Георгий Коколия',
118621: 'Михаил Акулов'}
for key in famous_players:
print('{}: {} - максимальное расстояние от игрока до других'
.format(famous_players[key],
nx.eccentricity(subgraph, v=key)))
Александр Друзь: 12 - максимальное расстояние от игрока до других
Анатолий Вассерман: 12 - максимальное расстояние от игрока до других
Максим Поташев: 12 - максимальное расстояние от игрока до других
Михаил Скипский: 12 - максимальное расстояние от игрока до других
Михаил Атепаев: 13 - максимальное расстояние от игрока до других
Николай Некрылов: 12 - максимальное расстояние от игрока до других
Георгий Коколия: 13 - максимальное расстояние от игрока до других
Михаил Акулов: 13 - максимальное расстояние от игрока до других
Получается, что сильная формулировка теории шести рукопожатий (любые два человека разделены не более чем пятью уровнями общих знакомых) неверна. Диаметр графа, скорее всего, равен 13-14.
А что насчёт более слабой формулировки (любые два человека в среднем разделены не более чем пятью уровнями общих знакомых)?
for key in famous_players:
paths = nx.shortest_path_length(subgraph, source=key).values()
print('{}: {} - среднее расстояние от игрока до других'
.format(famous_players[key],
sum(paths) / len(paths)))
Александр Друзь: 3.941461876893135 - среднее расстояние от игрока до других
Анатолий Вассерман: 3.7971107852140182 - среднее расстояние от игрока до других
Максим Поташев: 3.89353216101753 - среднее расстояние от игрока до других
Михаил Скипский: 3.8634887131481204 - среднее расстояние от игрока до других
Михаил Атепаев: 4.1443373857266215 - среднее расстояние от игрока до других
Николай Некрылов: 3.575478680390894 - среднее расстояние от игрока до других
Георгий Коколия: 3.608674497334192 - среднее расстояние от игрока до других
Михаил Акулов: 4.564102739819904 - среднее расстояние от игрока до других
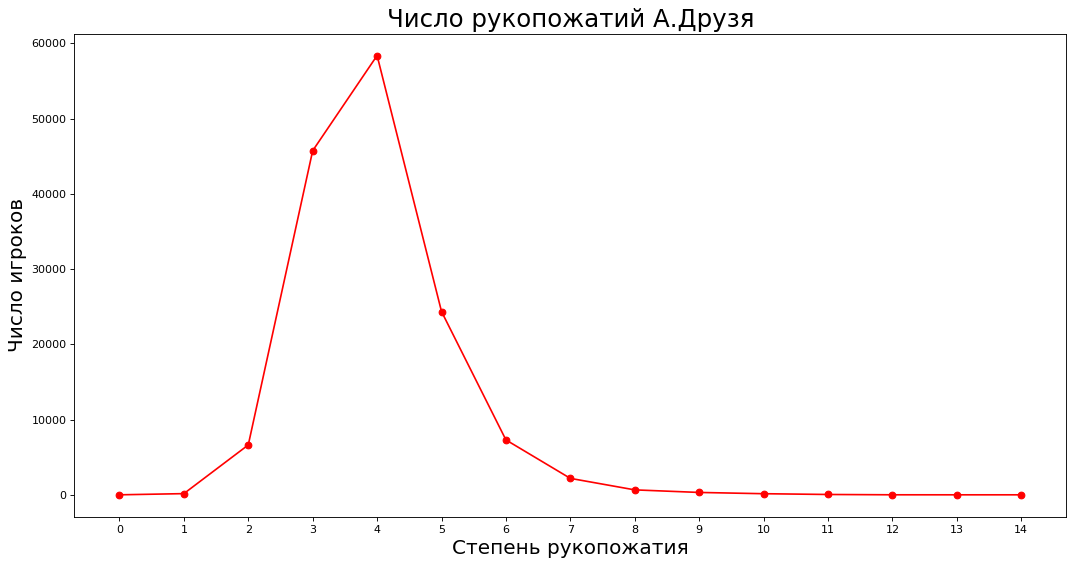
Если ослабить формулировку, то теория выполняется — в среднем между знатоками 4-5 уровней знакомств. Построим график, сколько людей знакомы со случайным знатоком А.Друзём напрямую, через одного, двух и т.д. знатоков.
paths = nx.shortest_path_length(subgraph, source=9808)
neighbours = [0] * 15
for k in paths:
neighbours[paths[k]] += 1
_count = 15
plt.figure(figsize=(16, 8), dpi=80)
plt.plot(range(_count),neighbours[:_count],'ro-') # in-degree
plt.xlabel('Степень рукопожатия', fontsize=18)
plt.xticks(range(_count))
plt.ylabel('Число игроков', fontsize=18)
plt.title('Число рукопожатий А.Друзя', fontsize=22)
plt.show()По оси X степень знакомства с А.Друзём (напрямую, через одного, двух и т.д.), по оси Y — количество знатоков, которые знакомы с А.Друзём таким образом.
Социальные графы
Т.к. строить граф на почти 200 тысяч человек не очень хорошая идея, сделаем проще: построим Керченскую компоненту связности и граф людей, связанных с автором.
Керченская компонента
little_v = list(sorted(nx.connected_components(G), key=len, reverse=True)[1])
little = G.subgraph(little_v)
plt.figure(figsize=(24, 12), dpi=200)
pos = nx.kamada_kawai_layout(little)
nx.draw(little, pos=pos, node_size=100, edge_color='gray',
node_color=[val for (node, val) in little.degree()], cmap=plt.cm.jet)
plt.show()
Видно разделение компоненты на команды. При этом команды связаны между собой с помощью, как правило, одного-двух общительных знатоков. В центре довольно небольшое ядро знатоков, игравших с большим количеством других игроков.
Граф одного человека
Найдём ближайших знакомых одного человека и посмотрим, насколько они связаны между собой. Для упрощения графа не будем добавлять самого человека (он и так со всеми связан)
id = 118622
ego_graph = [n for n in G.neighbors(id)]
#ego_graph.append(id)
ego_graph = G.subgraph(ego_graph)
plt.figure(figsize=(24, 16), dpi=200)
pos = nx.kamada_kawai_layout(ego_graph)
nx.draw(ego_graph, pos=pos, node_size=100, edge_color='gray',
node_color=[val for (node, val) in ego_graph.degree()], cmap=plt.cm.jet)
plt.show()
Граф существенно плотнее, различимо ядро из 10-15 человек, которые хорошо знакомы друг с другом. Размер максимальной клики равен 13.
Заключение
- В спортивном ЧГК познакомиться с человеком значительно труднее, чем в социальной сети, необходимо выйти в оффлайн и сыграть хотя бы один турнир. При этом знатоки разбросаны по всему земному шару. Тем не менее, среднее расстояние между знатоками действительно меньше пяти.
- На сайте рейтинга используется число Снятковского, которое является аналогом числа Эрдёша в мире ЧГК. Сам господин Снятковский занимает третье место в нашем рейтинге самых коммуникабельных знатоков.
- Код из статьи в моём гитхабе.
- За ценные замечания автор выражает благодарность командам "Белый шум" и "КПРФ", Михаилу Акулову, Вере Терентьевой и Firemoon.