Что из себя представляет тестирование и анализ алгоритмов? Давайте разберемся в этом на практике!

Недавно я стал участником дискуссии о том, что значит «тестировать алгоритм», или же что значит «заниматься разработкой тестов для алгоритмов». Увы, я не смог сформулировать для себя убедительного определения. На базовом уровне, скорее всего, вы будете определять основные правила алгоритма, давать ему какие-нибудь данные на вход и получать что-нибудь на выходе. Проверять результаты. Но я считаю, что этим все не исчерпывается, а именно мы можем оценить соответствие алгоритма его цели, соответствие данным, провести оценку альтернатив, адаптировать алгоритм к доступным системам и задачам, заниматься разработкой и проведением экспериментов, изучением и т. д.
Чтобы сформировать лучшее представление обо всем этом, я решил подробно исследовать эту тему. В этой статье я попытаюсь проанализировать и протестировать два алгоритма и посмотреть, куда это меня приведет. Начну я с более классических алгоритмов, в которых входные и выходные данные, и их отношения четко определены. В следующей статье я хочу рассмотреть алгоритмы, основанные на машинном обучении, где определение правильных результатов не столь четкое.
Выбранные алгоритмы
Поскольку моей целью было проанализировать тестирование и анализ алгоритмов, в самую первую очередь мне нужно было выбрать для работы какой-нибудь алгоритм. К моему счастью, Википедия предоставляет обширный список алгоритмов. Я выбрал две классики, бинарный поиск и расстояние редактирования Левенштейна. Сначала я проведу базовый тест и анализ бинарного поиска. Далее последует более широкий анализ Левенштейна.
Вообще я считаю, что тестирование алгоритма не в широком контексте упускает некоторые ключевые моменты из общего процесса. Поэтому я выбрал сферу применения для алгоритма Левенштейна таковой, чтобы придать моему тестированию и анализу некоторый контекст. Этот контекст представляет собой применение для сравнения дистанций редактирования цепочек РНК, а если быть точнее, частей структуры разных штаммов вируса COVID-19.
Бинарный поиск
Для начала — бинарный (двоичный) поиск. Это алгоритм, предназначенный для эффективного поиска элемента в списке с логарифмическим временем выполнения. В своих экспериментах я буду использовать набор данных имен IMDB и реализацию бинарного поиска на Python (позаимствованную из ответов со Stack Overflow).
Понимание алгоритма
При тестировании алгоритма мне для начала нужно понять, с чем я работаю. Чтобы сформировать некоторое базовое восприятие, я начну с рассмотрения бинарного поиска в сравнении с линейным. Линейный (последовательный) поиск — это очень примитивный алгоритм поиска, который просто проходит список по порядку в поисках совпадения. Он послужит основой для сравнения в данном анализе. Чтобы проиллюстрировать разницу и суть алгоритма бинарного поиска, давайте взглянем на фрагмент из 10 имен из набора данных IMDB:
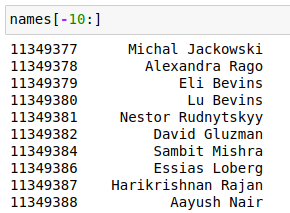
Я выбрал последние 10 имен из набора данных, потому что они выглядели достаточно рандомно. Бинарный поиск требует, чтобы входные данные были отсортированы, поэтому давайте сделаем это. После сортировки и переиндексации этот набор из 10 имен будет выглядеть следующим образом:
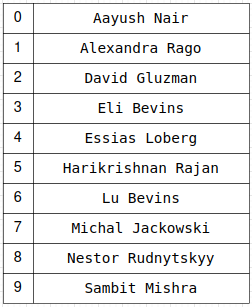
Чтобы лучше понять линейный и бинарный поиск, я сделал иллюстрацию процесса их работы над приведенном выше списком. Оба ищут “Lu Bevins”:
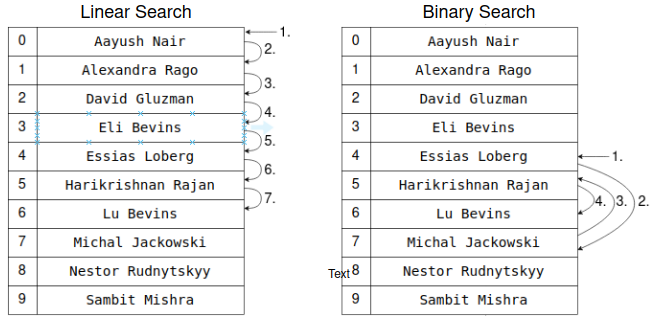
Линейный поиск всегда перебирает весь список с самого начала, пока не найдет совпадение. Список может иметь любой порядок. Бинарный поиск постоянно разбивает список на две части и сравнивает среднее значение с искомым (если оно больше искомого значения, то поиск осуществляется в первой половине, если меньше - то во второй), повторяя это в полученных фрагментах, пока не будет найдено совпадение или пока не закончатся элементы для проверки.
Хоть бинарный поиск — достаточно простой и хорошо известный алгоритм, выше я все-равно постарался показать, как я бы пытался его понять. Я считаю, что конкретные примеры и диаграммы помогают мне лучше вникнуть в суть алгоритма. Наличие доступа к средствам экспертов (в предметной области - StackOverflow и IMDB) для построения и проверки тоже очень помогает. Особенно с менее популярными алгоритмами.
Приведенный выше пример списка из 10 элементов очень мал и не иллюстрирует преимущества бинарного поиска. На больших объемах данных сравнение между линейным и бинарным поиском должно выглядеть следующим образом (ведь сложность логарифмическая):
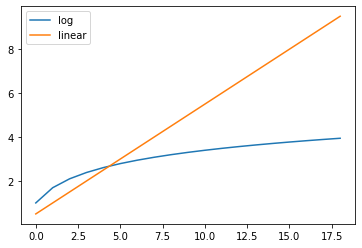
Такие предположения нужно проверять, поэтому дальше именно этим я и займусь.
Проверка вычислительной сложности
Обычно при тестировании и анализе алгоритмов нас очень интересует вычислительная сложность. Когда мы говорим о ней, мы думаем о ресурсах (время выполнения, память и т. д.), которые алгоритм использует в разных масштабах. В рамках этого алгоритма я сфокусируюсь на времени выполнения, хотя аналогичный анализ можно провести и для других ресурсов.
Чтобы изучить масштабируемость бинарного поиска, я нарезал из набора данных IMDB списки длиной от 10 до 1000 имен с шагом в 10 и выполнил как линейный, так и бинарный поиск по случайным элементам в этих списках.
Чтобы получить более статистически достоверные результаты, я провел эксперименты по 100 раз для каждого из этих списков. Для профилирования времени выполнения я использовал свою библиотеку codeprofile. На изображениях ниже показано среднее измеренное время выполнения по 100 запускам каждого из представленных размеров выборки в сравнении с теоретическим ожидаемым временем:
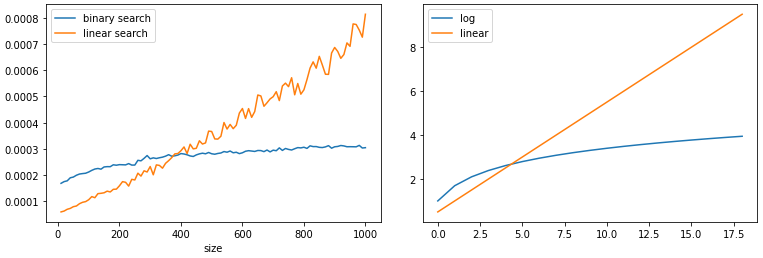
Приведенная выше статистика показывает, что полученные кривые соответствуют ожидаемой логарифмической кривой роста времени выполнения для бинарного поиска и линейному росту для линейного. Так что измерения совпадают с теорией (масштабы на рисунках разные из-за разных параметров, меня просто интересовали формы).
1000 элементов — это все еще очень маленький список для реальных измерений производительности. Выполнение того же эксперимента для выборок с количеством элементов от 10 до 1 миллиона (с 10-кратным шагом) более четко демонстрирует эффективность и преимущества бинарного поиска:
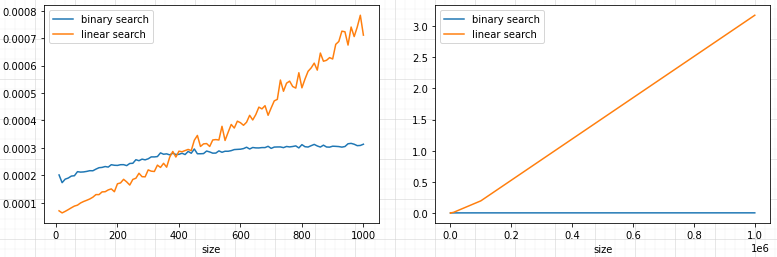
На приведенном выше изображении для списка размером в 1 миллион элементов разница настолько велика, что кривая бинарного поиска по сравнению с линейным поиском выглядит ровной плоской линией в окрестностях нуля. Основываясь на проведенных выше простых экспериментах, я могу сделать вывод, что предположения относительно вычислительной сложности верны.
Линейный и бинарный поиск являются хорошо известными и изученными алгоритмами, и их сложность тоже очень хорошо всем известна. Благодаря этому, они хорошо подходят для демонстрации того, как мы можем оценивать практические значения. Я обнаружил, что оценка практической вычислительной сложности реальных реализаций может преподносить сюрпризы, особенно если брать в расчет самые разные варианты использования пользовательских алгоритмов от третьих лиц.
Тестирование соотношений между входными и выходными данными
Знание вычислительной сложности — это хорошо, но нам также нужна уверенность в том, что реализация работает так, как задумано. Для бинарного поиска базовые тесты поиска выбранных имен, границ, разделения на категории и т. д. являются хорошими примерами. Я называю их тестами базовой гарантии (base assurance tests).
Чтобы масштабировать этот процесс, я использовал тестовый генератор из приведенного выше анализа вычислительной сложности от 10 до 1 миллиона и добавил к нему следующую проверку:
Правда ли, что для каждого найденного элемента линейный и бинарный поиск находят один и тот же индекс?
Я называю это ожидаемым/предполагаемым инвариантом данных/алгоритма. Я ожидал, что два алгоритма дадут одинаковые результаты для одних и тех же входных данных, и добавил это утверждение просто для дополнительной уверенности. Однако это утверждение было ошибочным, потому что индексы, найденные линейным и бинарным поиском, не всегда были одинаковыми даже для одних и тех же входных данных.
После некоторого размышления о работе алгоритмов и том, что могло вызвать эту разницу, я понял, что в наборе данных могут быть повторяющиеся имена. Быстрая проверка показала, что это так (ниже для примера приведены две строки):
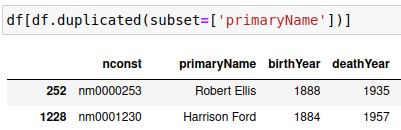
На изображении выше показано, что “Robert Ellis” и “Harrison Ford” имеют дубликаты. Давайте копнем немного глубже и найдем всех обладателей имени “Harrison Ford”:
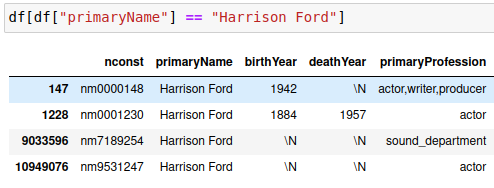
В этом наборе данных есть четыре разных человека с одним и тем же именем “Harrison Ford”. Установив наличие повторяющихся имен, было бы интересно посмотреть на некоторые сводные показатели, чтобы узнать, сколько их:
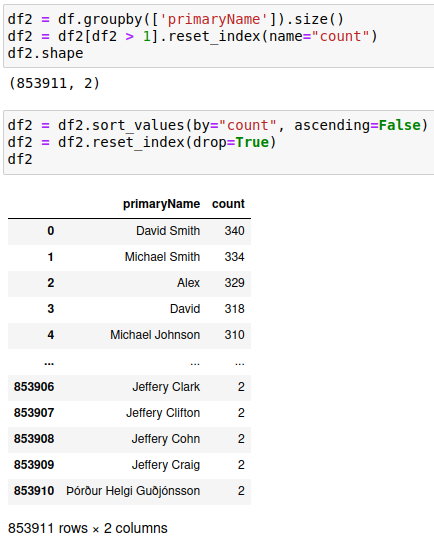
Приведенные выше цифры показывают, что в общей сложности 853911 (количество строк) различных имен имеют дубликаты. Тот, у кого больше всего дубликатов, — “David Smith”, повторяется 340 раз. Что вышеизложенное означает для результатов поиска наших алгоритмов? Из-за того, как работают эти два алгоритма, поиск “David Smith”, скорее всего, приведет к тому, что как линейный, так и бинарный поиск вернет нам разных “David Smith”. Линейный поиск всегда будет возвращать первое соответствие в списке, бинарный поиск может выдать любой результат из списка дубликатов.
Для меня это наглядно демонстрирует, как тестирование и анализ алгоритма помогают лучше понять как сам алгоритм, так и данные, с которыми он работает. И что по-хорошему следует делать предположения (или утверждения) о данных и самом алгоритме и проверять их в процессе тестирования. Наличие четкой цели и систематического подхода вам очень сильно помогут.
Кроме инвариантов в результатах алгоритма, их можно рассматривать и во входных данных. Например, бинарный поиск предполагает сортировку входных данных. Вопрос заключается в том, следует ли ограничить объем тестирования, ожидая, что среда (система в целом) обеспечит это сама, или ожидать, что реализация алгоритма должна брать на себя эту заботу. Я бы назвал это определением области действия алгоритма (algorithm scope) или теста.
На этом все на сегодня. В следующей части мы проанализируем расстояние Левенштейна на фрагментах РНК COVID-19.
Еще в 60-е годы прошлого века было замечено, что скорость разработки ПО падает по мере роста размера проекта. Инструменты разработки не могут изменить тенденции, а лишь замедлить и отсрочить неизбежное. SOLID является одной из практик, которая гарантирует неизменность скорости разработки.
Скоро состоится открытое занятие на тему «SOLID как условие постоянной скорости разработки», на котором мы разберем, почему SOLID принципы являются достаточным условием сохранения скорости разработки, рассмотрим простой и понятный механизм их применения для получения повторно используемого кода. Для всех заинтересованных регистрация доступна по ссылке.