Ищем логику в «американских горках» графика заражений Covid

Рисунок 1

Пики и падения, сжатия и растяжения, волна за волной всплесков и снижений: в течение полутора лет я ежедневно наблюдал за движениями этой кривой. График фиксирует количество новых обнаруженных случаев Covid-19 в США за каждый день с 21 января 2020 по 20 июля 2021 года. Это 547 дней, или ровно 18 месяцев. Бледные тонкие вертикальные полосы на фоне обозначают сырые ежедневные данные; ярко-синей линией обозначены суммарные средние значения за семь дней. (Другими словами, количество случаев за каждый день усредняется с количеством за шесть предыдущих дней.)

Я затрудняюсь объяснить крупномасштабные колебания этого графика. Если бы несколько лет назад меня спросили, как может выглядеть крупная эпидемия, то я бы пробормотал что-нибудь об экспоненциальном росте и угасании, и мог нарисовать примерно такую кривую:

Рисунок 2

Моя воображаемая эпидемия была намного проще реальной! Количество ежедневных заражений увеличивается, а затем снижается. Оно не колеблется, как нервный график фондовой биржи. У него нет сезонных всплесков и падений.

График, отслеживающий истинную частоту заболеваний, не меньше дюжины раз сменяет направление, а также имеет множество мелких изгибов. Большая гора посередине имеет холмы по обеим сторонам, а также альпийские долины между крутыми вершинами. Меня озадачивает вся эта структурная картина. Является ли она чистым шумом — результатом случайных флуктуаций, или же у неё есть какой-то движущий механизм, который мы должны узнать, какой-то переключатель, включающий и отключающий процесс заражения каждые несколько месяцев?

У меня есть несколько вариантов возможных объяснений, но я не осмелюсь утверждать, что какой-то из них верен. Однако я надеюсь убедить вас, что кое-что здесь требует объяснения.

Прежде чем двигаться дальше, я должен рассказать о своих источниках. Файлы данных, с которыми я работаю, курируются The New York Times на основании информации, собранной из отделов здравоохранения штатов и регионов. Сбор данных — это серьёзная работа; в Times проектом занимается более 150 сотрудников. Им нужно проверять отличающиеся друг от друга и постоянно меняющиеся политики предоставляющих отчётность учреждений, а затем разбираться, что делать, если получаемые числа выглядят сомнительно. (В июне у Флориды был день с –40 тысячами новых случаев.) Весь архив с данными, сейчас имеющий объём примерно 2,3 ГБ, свободно доступен на GitHub. Рисунок 1 моей статьи смоделирован по ежедневно обновляемому графику в Times.

Также мне нужно сделать несколько заявлений. Экспериментируя с этим набором данных, я не пытаюсь прогнозировать течение пандемии или даже спрогнозировать прошлое — разработать модель, достаточно точную для воспроизведения подробностей дат и величин, наблюдавшихся на протяжении последних полутора лет. Я совершенно точно не даю никаких рекомендаций по лечению или здравоохранению. Я просто озадаченный человек, ищущий простые механизмы, способные объяснить общую форму кривой заражений и, в частности, паттерн «американских горок», состоящий из повторяющихся «холмов» и «долин».

Пока на США обрушились четыре крупные волны заражений, а пятая волна сейчас начинает напоминать цунами. Хотя волны значительно различаются по высоте, похоже, что они накатывают на нас с определённой регулярностью. Я окинул взглядом Рисунок 1, и у меня сложилось впечатление, что период от пика до пика довольно стабилен и составляет примерно четыре месяца.

Периодические колебания эпидемических заболеваний уже много раз замечались ранее. Классическим примером является корь в Великобритании, еженедельные записи о которой велись с начала 18-го века. В 1917 году Джон Браунли изучил данные по кори при помощи разновидности анализа Фурье под названием «периодограмма». Он выяснил, что самый высокий пик в спектре частот возникал с периодом в 97 недель, вполне соответствуя распространённому наблюдению о том, что болезнь возвращается каждые два года. Но периодограммы Браунли изобиловали множеством более мелких пиков, показывающих, что ритм кори не представляет собой простой и равномерный барабанный бой.

[Особо примечательна работа М.С. Бартлетта, проделанная в 1950-х, которая стала одним из первых примеров компьютерного моделирования в эпидемиологии при помощи компьютера Манчестерского университета.]

Дальнейшие работы с использованием различных методик навели на мысль, что динамика эпидемии кори на самом деле может быть хаотичной и не имеющей долговременного порядка.

Механизм, лежащий в основе этого колебательного паттерна кори, легко понять. Заболевание поражает детей в первые школьные годы, и вирус настолько заразен, что распространяется по всему обществу за несколько недель. Следующая вспышка не может распространиться, пока новая когорта детей не достигнет соответствующего возраста. Для Covid-19 не существует такой возрастной зависимости, а гораздо более короткий период повторяемости даёт понять, что колебаниями может управлять другой механизм. Тем не менее, мне показалось, что стоит попробовать применить методы Фурье к данным на Рисунке 1.

Преобразование Фурье разлагает любую кривую, представляющую функцию от времени, в сумму простых синусоид и косинусоид различных частот. В примерах из учебников алгоритм работает как магия. Возьмём вот такую извилистую кривую:

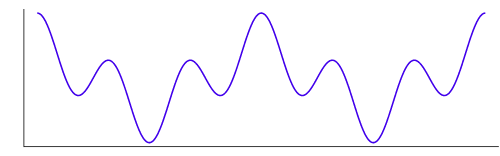
Рисунок 3

Передадим её в алгоритм преобразования Фурье, повернём рубильник и получим вот такой график, демонстрирующий коэффициенты различных частотных составляющих:

Рисунок 4

[Технические подробности: результатом классического преобразования Фурье являются комплексные коэффициенты с вещественной и мнимой частями. Я использую его разновидность под названием «дискретное косинусное преобразование», дающее вещественные коэффициенты. Исходная кривая сгенерирована функцией $\cos(x) + \cos(3x)$ на интервале от $inline$ до $4\pi$ .]

Только два коэффициента существенно отличаются от нуля, они соответствуют волнам, создающим два или шесть полных цикла, на интервале исходной кривой. Эти два коэффициента передают всю информацию, необходимую для воссоздания входной информации. Если начертить кривые, определяемые этими двумя коэффициентами, и поточечно сложить их, то мы получим копию оригинала.

Было бы здорово получить такое сжатое кодирование кривой Covid — пару чисел, объясняющие её рост и падение. Увы, это не так просто. Когда я передал данные Covid в алгоритм Фурье, то получил следующее

Рисунок 5

Более десятка коэффициентов со значительной величиной; некоторые положительны, другие отрицательны; на глаз невозможно увидеть очевидных паттернов. Этот спектр, как и более простой с Рисунка 4, содержит всю информацию, необходимую для воссоздания входящих данных. Я убедился в этом при помощи быстрого вычислительного эксперимента. Но взгляд на кучу коэффициентов не помог мне понять структуру кривой Covid. Преобразованная по Фурье версия ещё сильнее сбивает с толку, чем оригинал.

Из этого упражнения можно сделать вывод, что преобразование Фурье — и в самом деле магия: если вы хотите заставить его работать, вам необходимо освоить тёмные искусства. Я не волшебник по этой части; на самом деле, большинство моих столкновений с анализом Фурье завершалось слезами и психологической травмой. Без сомнения, кто-то более опытный сможет извлечь больше информации из этих чисел. Но сомневаюсь, что каким бы ни было мастерство владения Фурье, оно сможет привести к чёткому и сжатому описанию кривой Covid. Даже имея записи о кори за 200 лет, Браунли не смог выделить чёткий сигнал; имея данные за полтора года Covid, мы вряд ли добьёмся успеха.

Однако мой экскурс в сферу преобразований Фурье не был пустой тратой времени. Применив обратное преобразование Фурье к первым 13 коэффициентам (номера волн с 0 по 6), мы получим следующий набор кривых:

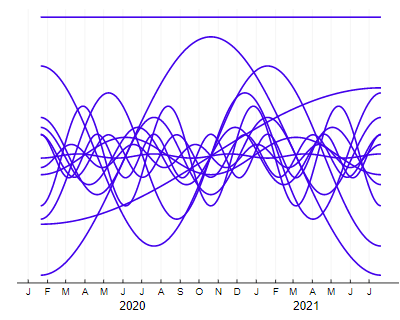
Рисунок 6

Выглядит беспорядочно, но сумма этих 13 синусоид даст нам довольно красивую сглаженную версию кривой Covid. На Рисунке 7 розовая область на фоне отображает данные Times, сглаженные усреднёнными значениями за семь дней. Гораздо более плавная синяя кривая — это форма волны, воссозданная из 13 коэффициентов Фурье.

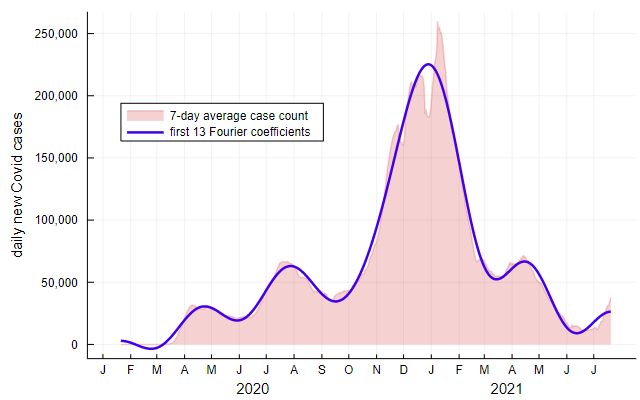
Рисунок 7

Воссозданная кривая повторяет контуры всех крупномасштабных особенностей кривой Covid, а серьёзные погрешности возникают только в конечных точках (которые всегда вызывают проблемы в анализе Фурье). Также кривой Фурье не удалось воссоздать три острых пика на вершине большого всплеска прошлой зимы, но не уверен, является ли это изъяном.

Давайте приглядимся к этим трём пикам. На графике ниже показан увеличенный вид двухмесячного интервала с 20 ноября 2020 года по 20 января 2021 года. Светлые полосы на фоне — это сырые данные по ежедневным новым случаям; тёмно-синяя линия — это усреднённые значения за семь дней, вычисленные Times.

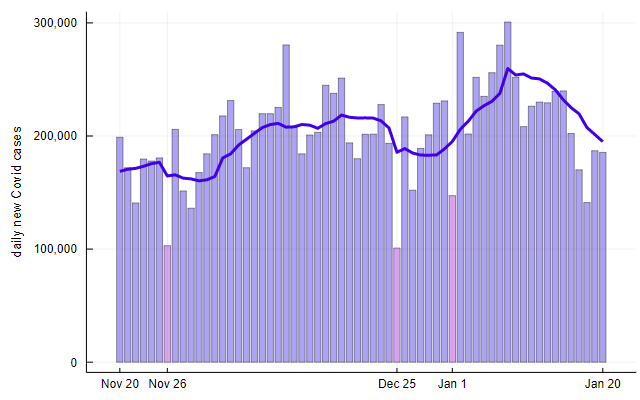
Рисунок 8

Пики и долины в этом виде такие же высокие/низкие как на Рисунке 1; они выглядят менее серьёзными только потому, что горизонтальная ось растянута в девять раз. Меня интересуют не пики, а снижения между ними. (В конце концов, трёх пиков бы не было без разделяющих их двух впадин.) Три точки данных, помеченных розовым цветом — это количество заражений, которое оказалось намного меньше, чем в окружающие дни. Обратим внимание на даты этих событий. 26 ноября — День благодарения в США в 2020 году, 25 декабря — Рождество, а 1 января — Новый год. Похоже, вирус на праздники уходит в отпуск, но на самом деле, разумеется, выходной брали медицинские работники и сотрудники сферы здравоохранения, поэтому многие случаи заражения в эти дни не фиксировались.

Но на этом история не заканчивается. Хотя праздники в этом графике проявились как нижние точки в развитии эпидемии, из-за семейных сборищ, религиозных служб, пиршеств и так далее они с большой вероятностью привели к повышению уровня заражений. (Прошлой осенью я писал о риске Дня благодарения.) Эти «дополнительные» заражения не отображались в статистике ещё несколько дней вместе со случаями, которые не диагностировались и не регистрировались в сами праздники. Поэтому каждый спад кажется глубже, потому что за ним следует всплеск.

В конечном итоге, кажется вероятным, что спады, создавшие тройной пик — это аномалия отчётности, а не отражение истинных изменений в частоте трансмиссии вируса. Следовательно, сглаживающая их кривая может лучше отображать то, что на самом деле происходит с популяцией.

Есть и ещё одно преобразование, сильно отличающееся от анализа Фурье, которое может кое-что ещё рассказать нам о данных. Производная кривой Covid по времени даёт нам частоту изменения скорости заражения — она положительна, когда эпидемия нарастает и отрицательна, когда она спадает. Так как мы работаем с последовательностью дискретных значений, вычисление произвольной тривиально: это просто последовательность разностей между соседними значениями.

Рисунок 9

Производная сырых данных (синяя) выглядит как показания сейсмографа в неспокойный день в Сан-Андреасе [прим. пер.: не в игре Rockstar, а в калифорнийском населённом пункте]. Три крупных праздничных аномалии, в которых количество ежедневных случаев изменяется на 100 тысяч в день, создают значительные выбросы. Более мелкие всплески, распространяющиеся на большей части 18-месячного интервала, вероятно связаны с семидневным циклом сбора данных, который обычно показывает увеличение количества заражений в будни и падение в выходные.

Усреднённое суммарное значение за семь дней призвано подавить этот еженедельный цикл, к тому же оно сглаживает более крупные флуктуации. Получившаяся кривая (красная) не только менее дёрганная, но и имеет гораздо меньшую амплитуду. (Для понятности я в два раза увеличил масштаб по вертикали.)

Наконец, восстановленная кривая, построенная суммированием 13 составляющих Фурье, образует производную кривую (зелёная), колебания которой напоминают волны на воде, даже при растяжении по вертикали в четыре раза.

Точки, в которых производные кривые пересекают ось абсцисс, сменяясь с положительной на отрицательную и наоборот, соответствуют пикам или спадам кривой количества заражений. Каждая точка пересечения с нулём — это момент смены направления тренда эпидемии, когда растущее ежедневное количество заражений начинает спадать, или падающая поворачивает и снова начинает увеличиваться. Синяя кривая сырых данных содержит 255 пересечений с остью, а красная усреднённая — 122 пересечения. Даже меньший показатель подразумевает, что тренд заражения меняется четыре-пять дней, что неправдоподобно; большинство этих перемен знаков возникает вследствие шума в данных.

Плавная зелёная кривая имеет девять пересечений с осью, большинство из которых, похоже, действительно сигнализирует о реальных изменениях в развитии эпидемии. Мне хотелось бы разобраться, что вызывает эти явления.

Вы подхватили вирус. (Сочувствую.) Несколько дней спустя вы заражаете несколько человек, которые спустя аналогичное количество дней заражает ещё больше людей. Таков механизм экспоненциального (или геометрического) роста. С каждым звеном в цепи распространения количество новых случаев умножается на коэффициент $inline$ , который является естественным коэффициентом развития эпидемии — средним количеством случаев, порождённых каждым заражённым человеком. Начавшись с единственного случая во время $inline$ , количество новых заражений в любой последующий момент времени $inline$ будет равно $inline$ . Если $inline$ больше $inline$ , даже совсем ненамного, то количество случаев увеличивается неограниченно; если $inline$ меньше $inline$ , эпидемия спадает.

Средняя задержка между моментом заражения и временем, когда вы сможете заражать других, называется инкубационным периодом. Я обозначу его как T_SP и сделаю его основной единицей измерения событий эпидемии. В случае Covid-19, один T_SP, вероятно, составляет около пяти дней.

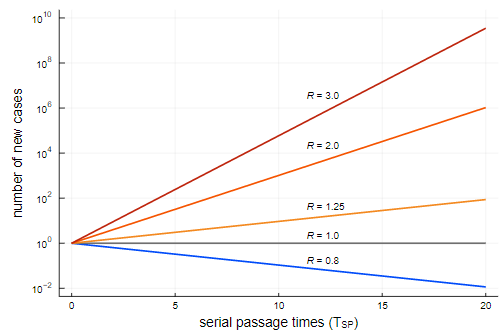
Экспоненциальный рост известен тем, что его нельзя контролировать. Если $inline$ , то количество случаев удваивается с каждой итерацией: $1, 2, 4, 8, 16, 32\dots$ . Оно увеличивается примерно в тысячу раз после 10 T_SP, и в миллион раз спустя 20 T_SP. Скорость роста становится такой крутой, что я не смогу даже отобразить её на графике, если только не в логарифмическом масштабе, где экспоненциальная траектория становится прямой линией.

Рисунок 10

Каково значение $inline$ для вируса SARS-CoV-2? Точно никто не знает. Число трудно замерить, и оно меняется со временем и местом. Ещё одно число, $inline$ , часто считается внутренним свойством самого вируса, показателем того, насколько легко он передаётся от человека к человеку. Центры по контролю и профилактике заболеваний США (Center for Disease Control and Prevention, CDC) предполагают, что $inline$ для SARS-CoV-2, вероятно, находится в интервале от $inline$ до $inline$ , а наиболее вероятно значение $inline$ . Это делает вирус более заразным, чем грипп, но менее заразным, чем корь. Однако CDC также опубликовал отчёт, в котором говорится, что $inline$ «легко недооценивать, неправильно интерпретировать и использовать». Я определённо был сбит с толку большинством прочитанных материалов по этой теме.

Каким бы ни было численное значение $inline$ , если оно больше $inline$ , то оно, вероятно, не может описать весь процесс течения эпидемии. При увеличении $inline$ значение $inline$ будет расти всё с большей скоростью, и не успеешь опомниться, как прогнозируемое число случаев превзойдёт общее население планеты. При $inline$ это абсурдное положение должно возникнуть примерно в $inline$ T_SP, то есть меньше чем за шесть месяцев.

Нам необходима математическая модель со встроенным ограничением роста. Так получилось, что наиболее известная в эпидемиологии модель имеет как раз такой механизм. Представленная почти сто лет назад В. Кермаком и А. Маккендриком из Королевского колледжа врачей в Эдинбурге, сегодня она называется моделью SIR, потому что разделяет человеческую популяцию на три подмножества, называемые «подверженные заболеванию» (susceptible, $\mathcal{S}$ ), «контагиозные» (infective, $\mathcal{I}$ ) и «излечившиеся» (recovered, $\mathcal{R}$ ). Изначально (прежде чем патоген попадает в популяцию) все люди имеют тип $\mathcal{S}$ . Подверженные заболеванию люди, вступившие в контакт с вирусом, становятся контагиозными — способными переносить заболевание на других подверженных заболеванию. Затем, после того, как болезнь каждого контагиозного человека пройдёт своё течение, эти люди переходят в подмножество излечившихся. Получив иммунитет к заболеванию, излечившиеся больше никогда не подвергаются заболеванию.

[В современных описаниях модели SIR обычно говорят, что $\mathcal{R}$ обозначает «устранённые» (removed), подразумевая, что излечение — это не единственный способ завершения заражения. Но сегодня я не хочу мрачных красок. Также обратите внимание на то, что я использую для $\mathcal{S}$ , $\mathcal{I}$ и $\mathcal{R}$ каллиграфический шрифт, чтобы вы не путали скорость роста $inline$ и подмножество излечившихся $\mathcal{R}$ .]

Эпидемия по модели SIR не может расти бесконечно по той же причине, по которой лесной пожар не может гореть, когда все деревья превратились в пепел. В начале эпидемии, когда заражению подвержена вся популяция, количество случаев может расти экспоненциально. Но позже рост замедляется, потому что каждому контагиозному сложнее найти подверженных заболеванию. Кермак и Маккендрик совершили интересное открытие: эпидемия угасает до того, как постигнет всю популяцию. То есть последний контагиозный излечивается до того, как заболеет последний подверженный заражению, оставляя остаточную популяцию $\mathcal{S}$ , никогда не подвергавшуюся болезни.

Сама модель SIR за последние несколько лет стала «вирусной». По ней есть куча туториалов в вебе, а также научные статьи и книги. (Рекомендую к прочтению Epidemic Modelling: An Introduction, by Daryl J. Daley and Joseph Gani. Или попробуйте Mathematical Modelling of Zombies, если ощущаете в себе смелость.) В большинстве случаев использования модели SIR, в том числе и в работе Кермака и Маккендрика, она представлена в виде дифференциальных уравнений. Я же продемонстрирую версию модели с дискретными интервалами времени ( $\Delta t$ , а не $inline$ ), потому что её проще объяснить и потому что она построчно преобразуется в компьютерный код. В представленных ниже уравнениях $\mathcal{S}$ , $\mathcal{I}$ и $\mathcal{R}$ — это вещественные числа в интервале $inline$ , представляющие пропорции некой популяции фиксированного размера.

$\begin{align} \Delta\mathcal{I} & = \beta \mathcal{I}\mathcal{S}\\[0.8ex] \Delta\mathcal{R} & = \gamma \mathcal{I}\\[1.5ex] \mathcal{S}_{t+\Delta t} & = \mathcal{S}_{t} - \Delta\mathcal{I}\\[0.8ex] \mathcal{I}_{t+\Delta t} & = \mathcal{I}_{t} + \Delta\mathcal{I} - \Delta\mathcal{R}\\[0.8ex] \mathcal{R}_{t+\Delta t} & = \mathcal{R}_{t} + \Delta\mathcal{R}\\[0.8ex] \end{align}$

Первое уравнение с $\Delta\mathcal{I}$ в левой части описывает сам процесс заражения — «рекрутирование» новых заражённых из популяции подверженных заражению. Количество новых случаев пропорционально произведению $\mathcal{I}$ и $\mathcal{S}$ , так как единственный способ распространения болезни — соединить того, у кого она есть, и того, кто может ею заразиться. Константа пропорциональности $\beta$ — это базовый параметр модели. Он обозначает частоту (на T_SP), с которой контагиозный человек встречается с другими достаточно близко, чтобы передать вирус.

Второе уравнение с $\Delta\mathcal{R}$ аналогичным образом описывает выздоровление. С точки зрения эпидемиологии вам необязательно полностью приходить в норму, чтобы выздороветь; выздоровление определяется как момент, когда вы больше не можете заражать других людей. Модель просто реализует эту идею, устраняя на каждом временном шаге фиксированную часть контагиозных. Эта доля задаётся параметром $\gamma$ .

После того, как первые два уравнения вычислили количество людей, меняющих своё состояние за конкретный временной интервал, последние три уравнения соответствующим образом обновляют сегменты популяции. Подверженные заражению теряют $\Delta\mathcal{I}$ членов; контагиозные получают $\Delta\mathcal{I}$ и теряют $\Delta\mathcal{R}$ ; излечившиеся получают $\Delta\mathcal{R}$ . На всём протяжении процесса общая популяция $\mathcal{S} + \mathcal{I} + \mathcal{R}$ остаётся постоянной.

В этой версии модели SIR соотношение $\rho = \beta / \gamma$ определяет естественную скорость роста, приближенно аналогичную $inline$ . Чем выше $\beta$ , тем быстрее происходит «рекрутинг» контагиозных; чем ниже $\gamma$ , тем дольше они остаются заразными. Любое из изменений этих параметров меняет скорость роста $\rho$ , однако скорость также зависит от $\mathcal{S}$ и $\mathcal{I}$ .

[В современной литературе скорость $\beta / \gamma$ обычно представляют не просто как аналог $inline$ , а как определение $inline$ . Я отказываюсь следовать этой практике, поскольку $inline$ уже и так имеет слишком много определений. Использовав символ $\rho$ , я повторил прецедент Дэвида Кендалла из статьи 1956 года.]

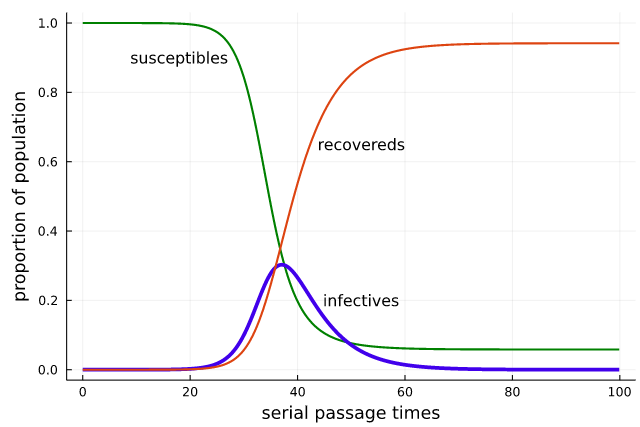
Вот что произойдёт, если привести модель в движение. На этом прогоне я присвоил значения $\beta = 0.6$ и $\gamma = 0.2$ , то есть $\rho = 3.0$ . Также нам нужно указать исходную пропорцию контагиозных; я выбрал $10^{-6}$ или, иными словами, один на миллион. Модель выполнялась в течение 100 T_SP с временным интервалом $\Delta t = 0.1$ T_SP; следовательно, всего было 1000 итераций.

Рисунок 11

Позвольте обратить ваше внимание на некоторые особенности этого графика. В начале кажется, что многие недели ничего не происходит, а затем внезапно из тихих вод возникает огромная синяя волна. Начав с одного случая в популяции миллион человек для достижения одного случая на тысячу нужно 18 T_SP, но всего ещё 12 T_SP, чтобы достичь одного на десяток.

Обратите внимание, что популяция контагиозных достигает пика рядом с местом пересечения подверженных заражению и выздоровевших, то есть где $\mathcal{S} = \mathcal{R}$ . Это соотношение остаётся истинным при широком интервале значений параметров. Это неудивительно, ведь весь процесс эпидемии работает как механизм по превращению подверженных заражению в выздоровевших с кратким переходом через стадию контагиозных. Но как и предсказали Кермак с Маккендриком, преобразование проходит не до завершения. В конце примерно 6% популяции остаётся в категории подверженных заражению, а для их заражения больше не осталось контагиозных. Такое состояние называется коллективным иммунитетом: популяция подверженных заражению настолько мала, что большинство контагиозных излечивается до того, как найдёт, кого заразить. Это конец эпидемии, однако он происходит после того, как заболеет 90 с лишним процентов людей. (Я бы не назвал такую ситуацию победой над вирусом.)

Категорию $\mathcal{I}$ в модели SIR можно взять как замену суммы новых случаев, отслеживаемых в данных Times. Эти две переменные не совсем одинаковы — контагиозные остаются в категории $\mathcal{I}$ , пока не выздоровеют, а новые случаи считаются только в день их фиксации, но они очень похожи и приблизительно пропорциональны одна другой. И это приводит нас к основному выводу, который я хочу сделать о модели SIR: синяя кривая на Рисунке 11 для контагиозных выглядит совершенно непохоже на соответствующую сумму новых случаев на Рисунке 1. В модели SIR количество контагиозных изначально почти равно нулю, резко поднимается до пика, а затем постепенно снижается до нуля, и больше никогда не поднимается. Это одногорбый верблюд. Однако «американские горки» кривой Covid совершенно иные.

Подробная геометрия кривой $\mathcal{I}$ зависит от значений, присвоенных параметрам $\beta$ и $\gamma$ . Изменение этих переменных способно укорачивать или удлинять кривую, увеличивать или уменьшать её амплитуду. Но ни одно сочетание параметров не даст многочисленных взлётов и падений кривой. В этих уравнениях нет колебательных решений.

Модель SIR показалась мне настолько правдоподобной, что она или какой-то её вариант должен быть правильным описанием естественного течения эпидемии. Но это не означает, что она может объяснить происходящее прямо сейчас с Covid-19. Ключевым элементом модели является насыщение: распространение заболевания приостанавливается, когда для заражения остаётся слишком мало подверженных ему. Это не могло вызвать резкое падение случаев Covid в начале января этого года или более ранние снижения, начавшиеся в апреле и июле 2020 года. Во время этих событий мы и близко не были к насыщению, да и сейчас тоже. (Пока я не рассматриваю влияние вакцинации и вернусь к этой теме ниже.)

На Рисунке 11 присутствует драматическая тройная точка, в которой каждая из трёх категорий составляет примерно треть от общей популяции. Если мы спроецируем эту ситуацию на США, то получим (в очень округлённых числах) 100 миллионов активных заражений, ещё 100 выздоровевших людей и третьи сто миллионов, которые пока избежали заражения (но большинство из которых подхватит его в последующие недели). Такие порядки величин несравнимы с нынешними. 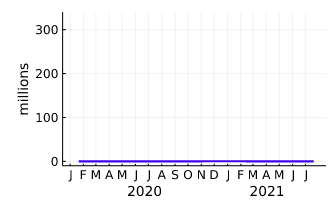Суммарное количество случаев, соединяющее в себе категории $\mathcal{I}$ и $\mathcal{R}$ , приближается к 37 миллионам или 11% от населения США.

Рисунок 12

Даже истинное количество случаев вдвое выше официального, мы пока далеко от критичной тройной точки модели. Судя по перспективам модели SIR, мы всё ещё находимся на ранних стадиях эпидемии, где количество случаев слишком мало, чтобы увидеть их на графике. (Если изменить масштаб Рисунка 1 так, чтобы ось y растянулась на всё население США в 330 миллионов, то вы получите показанный на Рисунке 12 плоский график.)

Если мы всё ещё находимся в начале кривой, в условиях резкого экспоненциального роста, то легко понять резкие ускорения, наблюдавшиеся в худшие моменты эпидемии. Сложно только объяснить повторяющиеся замедления распространения вируса, прерывающие кривую Covid. В модели SIR переломный момент возникает, когда у вируса начинают заканчиваться жертвы, но это единовременное явление, и мы до него ещё не добрались. В чём же причина глубоких впадин на кривой Covid газеты Times?

Среди прочих мыслей, сразу же приходящих в голову, одним из серьёзных претендентов является обратная связь. У всех нас есть доступ к информации в реальном времени о состоянии эпидемии. Мы получаем её от правительственных учреждений, новостных медиа, идиотов из Facebook и при личном общении с семьёй, друзьями и соседями. Думаю, большинство из нас соответственно реагирует на эти сообщения, изменяя наши меры предосторожности согласно с воспринимаемой серьёзностью угрозы. Когда снаружи страшно, мы залегаем на дно и надеваем маски. Когда опасность снижается, можно снова тусоваться! Я с лёгкостью могу представить сценарий, при котором такие многократные перемены в мерах предосторожности приводят к колебаниям в возникновении случаев заболевания.

Если эта гипотеза окажется истинной, то она может служить источником и надежды, и недовольства. Надежды, потому что интервалы снижения заражений дают понять, что наши средства по борьбе с эпидемией достаточно эффективны. Недовольства, потому что рост заражений показывает, что мы не используем эти средства максимально хорошо. Взгляните снова на кривую Covid на Рисунке 1, и в частности на резкое падение после зимнего пика. В начале февраля частота новых случаев упала на 30 тысяч в неделю. На первые три недели месяца скорость уменьшилась вдвое. Что бы мы тогда ни делали, это сработало идеально. Если бы мы просто продолжили двигаться по той же траектории, количество случаев в начале марта снизилось бы до нуля. Вместо этого снижение сначала стало горизонтальным, а затем снова превратилось в подъём.

Ещё один шанс у нас был в июне. На протяжении апреля и мая количество новых случаев стабильно снижалось, с 65 тысяч до 17 тысяч с темпом примерно -800 случаев в день. Если бы мы смогли сохранять эту скорость ещё всего три недели, но в конце июня бы пересекли финишную черту. Но тренд снова изменил направление и сейчас мы снова вернулись к 100 с лишним тысячам случаев в день.

На самом ли деле эти бессмысленные взлёты и падения вызваны влиянием обратной связи? Я не знаю. Особенно не уверен я в части истории с «если» — мысли о том, что если бы мы продержались ещё несколько недель, то вирус был бы уничтожен, или почти уничтожен. Но эту мысль стоит запомнить.

Возможно, мы можем узнать больше, создав петлю обратной связи в модели SIR и посмотрев на динамику колебаний. Отрицательная обратная связь — это всё, что замедляет скорость распространения, когда скорость высока, и усиливает её, когда она низка. Такой механизм противоположности можно добавить в модель несколькими способами. Наверно, самым простым будет порог локдауна: если количество заражённых поднимается выше определённого числа, все уходят в изоляцию; когда уровень $\mathcal{I}$ снова падает ниже порогового значения, все меры предосторожности и ограничения снимаются. Это правило «всё или ничего», благодаря чему его легко реализовать. Нам нужна константа, обозначающая пороговый уровень и новый коэффициент (который я назову $\varphi$ от слова fear, «страх»), которые мы вставим в уравнение $\Delta \mathcal{I}$ :

$\Delta\mathcal{I} = \beta \varphi \mathcal{I} \mathcal{S}$

Коэффициент $\varphi$ равен 1, если значение $\mathcal{I}$ ниже порогового и $inline$ , когда оно поднимается выше. Он прекращает все новые заражения после достижения порога, и начинает их снова, когда скорость заражения падает.

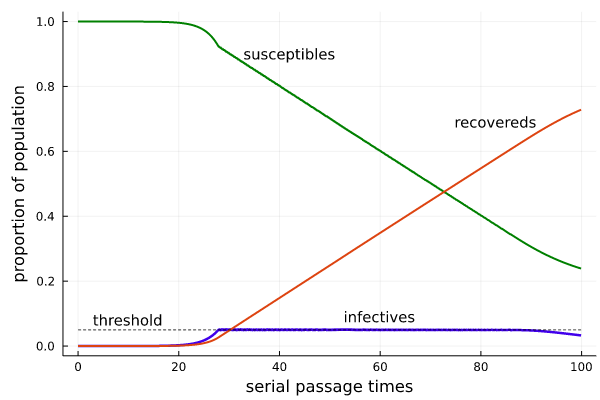
Создаст ли эта схема колебания в кривой $\mathcal{I}$ ? Строго говоря, да, но этого ни за что не скажешь, глядя на график.

Рисунок 13

Петля обратной связи служит в качестве системы контроля, как термостат, отключающий и включающий отопление для поддержания заданной температуры. В данном случае петля обратной связи обеспечивает стабильность контагиозной популяции на пороговом уровне, равном 0,05. При ближайшем рассмотрении оказывается, что $\mathcal{I}$ колеблется рядом с пороговым уровнем, но с таким коротким периодом и крошечной амплитудой, что волны невидимы. Значение колеблется вверх и вниз от 0,049 до 0,051.

Чтобы получить колебания макроуровня, нам недостаточно обратной связи. Показанный выше график SIR взят из модели, сочетающей обратную связь с задержкой между измерением состояния эпидемии и реакцией на эту информацию. Введение подобной задержки — не единственный способ обеспечить колебания модели, но он определённо выглядит реалистично. На самом деле, модель без задержки, при которой общество мгновенно реагирует на любое изменение количества случаев, кажется совершенно нереалистичной.

Рисунок 14

Модель на Рисунке 14 использует те же параметры, $\beta = 0.6$ и $\gamma = 0.2$ , как и в версии с Рисунка 13, а также тот же порог локдауна 0,05. Отличается она только временем совершения событий. Если количество заражённых поднимается выше порога в момент $inline$ , то меры контроля вступают в силу только в $inline$ ; тем временем, заражения продолжают распространятся по популяции. Задержка и выброс вверх на пути вверх соответствуют задержке и выбросу вниз в другой половине цикла, когда локдаун длится в течение трёх T_SP после того, как порог пересечён вниз.

С этими параметрами и настройками модель создаёт четыре цикла с уменьшающейся амплитудой и увеличивающейся длиной волны. (Дальнейшие циклы невозможны, потому что $\mathcal{I}$ остаётся ниже порогового значения.) Эти четыре острых пилообразных пика не очень похожи на колебания кривой Covid. Если мы по-прежнему будем рассматривать гипотезу обратной связи, то нам нужны более сильные доказательства. Но эта модель очень груба, её можно дополнить и усовершенствовать.

На самом деле, я очень хочу верить, что обратная связь может быть основным компонентом колебательной динамики Covid-19. Было бы утешительно осознавать, что наши меры по борьбе с эпидемией имеют столь мощный эффект, и мы обладаем определённой степенью контроля над своей судьбой. Но мне с трудом удаётся сохранять эту веру. Во-первых, я должен заметить, что наши меры противодействия не всегда были правильными. В первую волну эпидемии, когда характеристики вируса были почти неизвестны, людям не рекомендовали пользоваться масками (за исключением медицинского персонала) и много внимания уделялось мытью рук, перчаткам и обеззараживанию поверхностей. Не говоря уже о советах пить отбеливатель. Вероятно, эти меры были не особо эффективны в противодействии вирусу, но волна всё равно спала.

Ещё одним источником сомнений является то, что волноподобные колебания не уникальны для Covid-19.

Рисунок 15

Напротив, они кажутся общей характеристикой эпидемий во многих местах и эпохах. Эпидемия испанки 1918-1919 годов имела по крайней мере три волны. На Рисунке 15, источником которого Википедия называет CDC, показаны смерти от испанки на 1000 человек в Великобритании. Эти подъёмы выглядят ужасно знакомо. Они так похожи на волны Covid, что кажется логичным искать общую их причину. Но если оба паттерна — результаты эффекта обратной связи, то мы должны предположить, что меры по обеспечению здравоохранения, предпринятые век назад, в разгар Первой мировой, работали так же хорошо, как и современные. (Мне хочется думать, что мы всё-таки добились какого-то прогресса.)

Меня беспокоит один аспект модели SIR. В формулировке Кермака и Маккендрика модель считает заражение и выздоровление симметричным зеркальным процессом, каждый из которых описывается экспоненциальной функцией. Экспоненциальное правило для инфекций имеет смысл с точки зрения биологии. Можно получить вирус только от того, кто уже его подхватил, поэтому количество новых заражений пропорционально количеству существующих. Но выздоровление отличается от этой ситуации — оно не заразно. Хотя длительность заболевания может в определённой степени варьироваться, нет никакой причины предполагать, что она зависит от количества других одновременно болеющих людей.

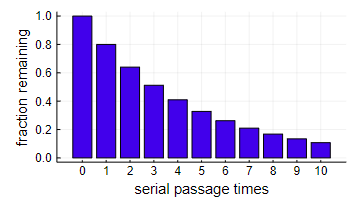
В модели фиксированная доля заражённых $\gamma \mathcal{I}$ выздоравливает через каждый временной интервал.

Рисунок 16

При $\gamma = 0.2$ это правило создаёт экспоненциальное распределение, показанное на рисунке 16. Представим, что какая-то большая группа людей заразилась одновременно, в $inline$ . Во время $inline$ пятая часть заражённых выздоровела, а 80% когорты по-прежнему остались контагиозными. В $inline$ пятая часть оставшихся 80% устраняется из категории контагиозных, оставляя 64%. И так далее. Даже после 10 T_SP больше 10% исходной группы останется контагиозным.

Длинный хвост этого распределения соответствует заболеваниям, сохраняющимся в течение многих недель. Такие случаи существуют, но они очень редки. Согласно данным CDC, большинство пациентов с Covid не имеют обнаруживаемого «способного к размножению вируса» спустя 10 дней после возникновения симптомов. Даже в самых серьёзных случаях, у пациентов с имунной недостаточностью, максимальным пределом являются 20 суток контагиозности.

[Не знаю, кто первым заметил, что экспоненциальное распределение времени выздоровления слишком обобщено, но это точно был не я. В 2001 году Алун Ллойд писал об этой теме в контексте эпидемии кори (Theoretical Population Biology Vol. 60, No. 1, pp. 59–71).]

Эти наблюдения намекают о возможности другой стратегии моделирования выздоровления. Вместо того, чтобы предполагать выздоровление фиксированной доли пациентов через каждый временной интервал, мы можем получить более точную аппроксимацию истины, предположив, что все пациенты выздоравливают (или, по крайней мере, становятся неконтагиозными) спустя фиксированное время болезни.

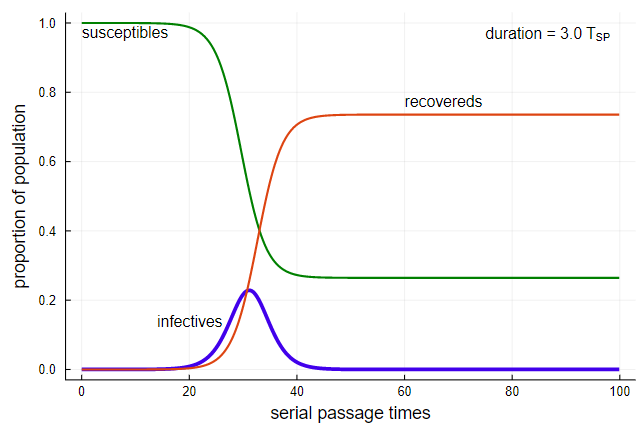
Модифицировать модель, добавив фиксированный период контагиозности, не очень сложно. Мы можем отслеживать заражённых при помощи структуры данных под названием «очередь». Каждая новая группа новых «рекрутированных» заболевших отправляется в конец очереди, а затем с каждым временным интервалом движется на шаг вперёд. Спустя $inline$ шагов (где $inline$ — длительность заболевания) группа достигает начала очереди и присоединяется к компании выздоровевших. Вот что происходит при $inline$ T_SP:

Рисунок 17

В этом примере я выбрал 3 T_SP, потому что это значение близко к медианной длительности в экспоненциальном распределении на Рисунке 11, а поэтому должно напоминать предыдущий результат. И приблизительно так и происходит. Как и на Рисунке 11, пик кривой количества контагиозных находится недалеко от места пересечения подверженных заражению и выздоровевших. Но пик никогда не поднимается так высоко; и по очевидным причинам всегда гораздо быстрее угасает. В результате этого эпидемия завершается с гораздо большим количеством подверженных заражению, которых не коснулась болезнь — больше 25%.

Длительность заболевания в 3 T_SP, или примерно 15 дней, всё равно сильно больше типичной длительности по оценкам CDC. Укоротив очередь до 2 T_SP, то есть примерно до 10 дней, мы ещё сильнее преобразуем результат. Теперь кривые подверженных заражению и выздоровевших никогда не пересекаются, и почти после завершения эпидемии неинфицированной остаётся почти 70% от популяции подверженных заражению.

Рисунок 18

Рисунок 18 чуть ближе к описанию к текущей ситуации с Covid в США, чем другие модели, рассмотренные ранее. Нельзя сказать, что форма кривой напоминает данные, но общая величина или интенсивность эпидемии ближе к наблюдаемым уровням. Из всех представленных выше моделей эта первая достигает естественного предела, не касаясь большинства популяции. Возможно, мы нашли что-то интересное.

С другой стороны, есть пара причин быть осмотрительными. Во-первых, с такими параметрами первоначальный рост эпидемии чрезвычайно медленен; для того, чтобы заражения оказали заметный эффект на популяцию, требуется 40 или 50 T_SP. Это сильно больше шести месяцев. Во-вторых, мы по-прежнему имеем дело с одногорбым верблюдом. Хотя большинство населения осталось незатронутым, эпидемия завершила своё течение и второй волны не будет. Нам по-прежнему не хватает чего-то важного.

Прежде чем завершить с этой темой, я хочу указать на то, что конечное время распространения инфекции обеспечивает нам особую точку управления для контроля распространением заболевания. Размножающиеся в вашем организме вирусы должны найти нового носителя за одну-две недели, иначе они столкнутся с вымиранием. Следовательно, если мы сможем полностью изолировать каждого человека в стране всего на две-три недели, то с эпидемией будет покончено. Разумеется, мы не сможем поместить всех и каждого в одиночное заключение (да это и неприемлемо с точки зрения морали), но мы можем максимально стремиться к этому, активно препятствуя любым видам контактов между людьми. Тестирование, отслеживание и карантины помогут справиться с оставшимися случаями. Я считаю, что очень строгий, но короткий локдаун будет и более эффективным, и менее разрушительным, чем очень вольный и длящийся месяцами. Другие стратегии нацелены на сглаживание кривой, а эта — на разрыв цепи.

Когда Covid появился в конце 2019 года, его вскоре назвали пандемией, и это означало, что он крупнее эпидемии и что он повсюду. Но он не был повсюду одновременно. Вспышки скакали от региона к региону и от страны к стране. Возможно, мы должны рассматривать пандемию не как единое глобальное событие, а как множество более локализованных всплесков.

Предположим, что мелкие кластеры заражений возникают в случайные моменты, длятся в течение своего развития, а потом затихают. Случайным образом множество географически изолированных кластеров может быть активно на протяжении одинакового интервала дат, что даёт большой скачок в суммарном количестве случаев по стране. Случайные флуктуации также могут создавать промежутки распространения затишья, что вызывает падение общенациональной кривой.

Мы можем проверить эту идею на простом вычислительном эксперименте, смоделировав популяцию, разделённую на $inline$ кластеров или сообществ. Для каждого кластера модель SIR генерирует кривую, имеющую пропорцию контагиозных как функцию от времени. Время инициации каждой из таких миниэпидемий выбирается случайно и независимо. Суммирование $inline$ кривых даёт общее количество случаев для страны в целом, тоже как функцию от времени.

Прежде чем смотреть на графики, сгенерированные этим процессом, можете попробовать догадаться, чем закончился эксперимент. В частности, как форма общенациональной кривой меняется при увеличении количества локальных кластеров?

Если есть только один кластер, то национальная кривая, очевидно, будет идентичной траектории болезни в этом одном месте. При двух кластерах есть высокая вероятность того, что они не будут особо совпадать, поэтому национальная кривая, вероятно, будет иметь два горба с глубокой долиной между ними. При $inline$ или $inline$ проблема наложения становится более серьёзной, но суммарная кривая всё равно, скорее всего, будет иметь $inline$ горбов, возможно, с меньшими падениями между ними. Прежде чем я увидел результаты, я сделал предположение о поведении суммы при дальнейшем увеличении $inline$ : я думал, что суммарная кривая всегда будет иметь приблизительно $inline$ пиков, но разность высот между пиками и долинами должна стабильно становиться меньше. Следовательно при больших $inline$ суммарная кривая будет иметь множество мелких всплесков, достаточно маленьких, чтобы общая кривая выглядела как один широкий плоский гамак.

Но хватит о моей интуиции. Вот два примера суммарных кривых, сгенерированных кластерами $inline$ миниэпидемий, одна кривая для $inline$ , вторая для $inline$ . Истории отдельных кластеров показаны тонкими красными линиями; суммы показаны синим. Все кривые отмасштабированы так, чтобы максимальный пик суммарной кривой касался 1,0.

Рисунок 19

Моё предположение о «широком плоском гамаке» со множеством мелких всплесков оказалось совершенно неверным. Количество пиков не увеличивается пропорционально $inline$ . На самом деле, обе суммарные кривые на Рисунке 19 имеют четыре отчётливых пика (может быть, пять в правом примере), хотя количество кривых, влияющих на сумму, в одном случае равно только шести, а в другом — пятидесяти.

[Технические подробности: время инициирования кластеров выбирается случайно и равномерно в интервале от 0 до 80. $\beta$ — это случайная величина, распределённая по нормальному закону со средним значением 0,6 и стандартным отклонением 0,1, обеспечивающая вариативность интенсивности и длительности отдельных субэпидемий. Первоначальный уровень контагиозных составляет 0.001.]

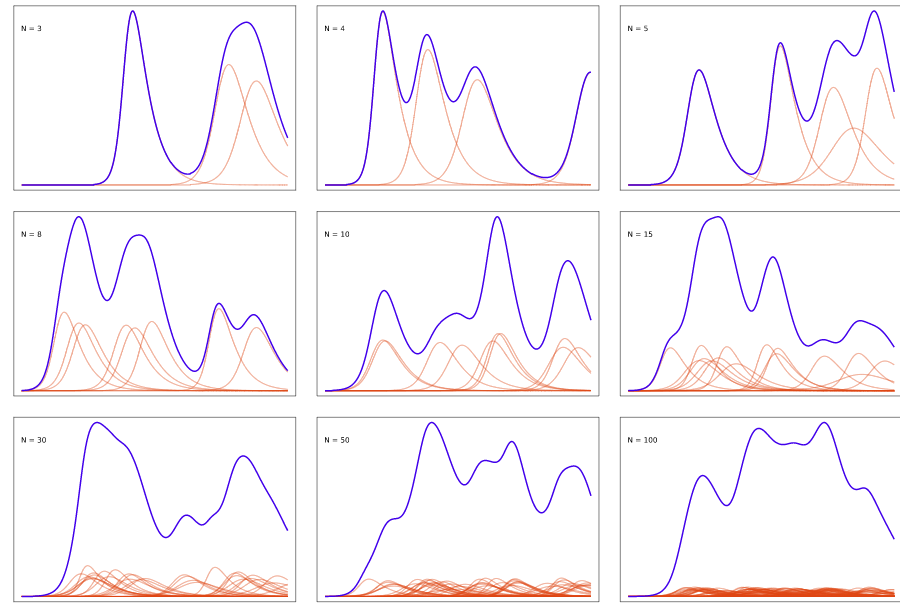
Должен признаться, что два примера с Рисунка 19 были выбраны не случайно. Я выбрал их, потому что они выглядели красиво и иллюстрировали утверждение, которое я хотел сделать, а именно что количество пиков в суммарной кривой остаётся почти постоянным, вне зависимости от значения $inline$ . На Рисунке 20 представлена более репрезентативная выборка, выбранная без намеренного отклонения, но снова демонстрирующая, что количество пиков не зависит от $inline$ , хотя с ростом $inline$ количество разделяющих эти пики долин растёт.

Рисунок 20

Похоже, из этих симуляций можно сделать вывод о том, что почти любая коллекция миниэпидемий со случайным временем возникновения всего за несколько волн комбинируется, образуя макроэпидемию. Количество пиков не всегда равно четырём, но редко намного отдаляется от этого числа. Гистограммы на Рисунке 21 являются численным доказательством этого утверждения. 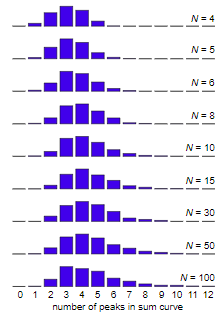В них зафиксировано распределение количества пиков в суммарной кривой для значений $inline$ в интервале от 4 до 100. Каждый работ столбцов отображает 1000 повторений процесса. Во всех случаях пики относятся к $inline$ , $inline$ или $inline$ .

Рисунок 21

Но вопрос в следующем: почему $4 \pm 1$ ? Почему мы продолжаем встречать конкретно эти числа? Если $inline$ , количество суммируемых составляющих, так мало влияет на это свойство суммарной кривой, то что же им управляет? Я долгое время задавался этими вопросами, пока мне не пришла в голову полезная аналогия.

Предположим, что у нас есть группа синусоид, имеющих одинаковую частоту $inline$ , но со случайно выбранными фазами; то есть все волны имеют одинаковую форму, но сдвинуты влево или вправо по оси $inline$ на случайные величины. Как будет выглядеть сумма этих волн? Ответ таков: как ещё одна синусоида с частотой $inline$ . Этот мелкий факт был известен уже много веков (по крайней мере, со времён Эйлера) и его несложно доказать, но он каждый раз немного шокирует меня, когда я с ним сталкиваюсь. Думаю, подобный аргумент может объяснить и поведение суммы кривых SIR, даже хотя эти кривые не синусоидальны. Составляющие кривые SIR имеют период от 20 до 30 T_SP. В прогоне модели, длящемся 100 T_SP, эти кривые можно рассматривать как имеющие частоту от трёх до пяти циклов на период эпидемии. Их сумма должна быть волной с той же частотой — чем-то вроде кривой Covid, с её четырьмя (или четырьмя с половиной) выделяющимися горбами. В поддержку этого утверждения можно сказать, что когда я прогоняю модель в течение 200 T_SP, то получаю суммарную кривую с семью или восемью пиками.

Меня заинтриговала идея о том, что эпидемия может возникать циклическими волнами не потому, что есть что-то особенное в поведении вируса или человека, а из-за математического процесса, напоминающего интерференцию волн. Это очень изящная идея, прикрывающая часть контринтуитивной математики и воздействующая на тему, которая чрезвычайно важна для всех нас. Однако, увы, более внимательное изучение данных Covid даёт нам понять, что природа не разделяет моей гордости от суммирования волн со случайными фазами.

Рисунок 22, тоже созданный на основе данных, извлечённых из архива Times, содержит график 49 кривых, представляющих распределение по времени количества случаев в 48 штатах и округе Колумбия. Я разделил их по регионам, и в каждой группе пометил кривую с наибольшим пиком. Мы уже знаем, что эти кривые вместе дают сумму с четырьмя высокими пиками; с этого и начинается наше расследование. Однако 49 кривых не подтверждают утверждение о том, что эти пики могут создаваться суммированием миниэпидемий со случайным временем возникновения. Колебания 49 кривых не имеют случайного возникновения; между ними есть сильные корреляции. И многие из кривых имеют множественные горбы, которые невозможны, если каждая миниэпидемия должна работать как в модели SIR, выполняемой до её завершения.

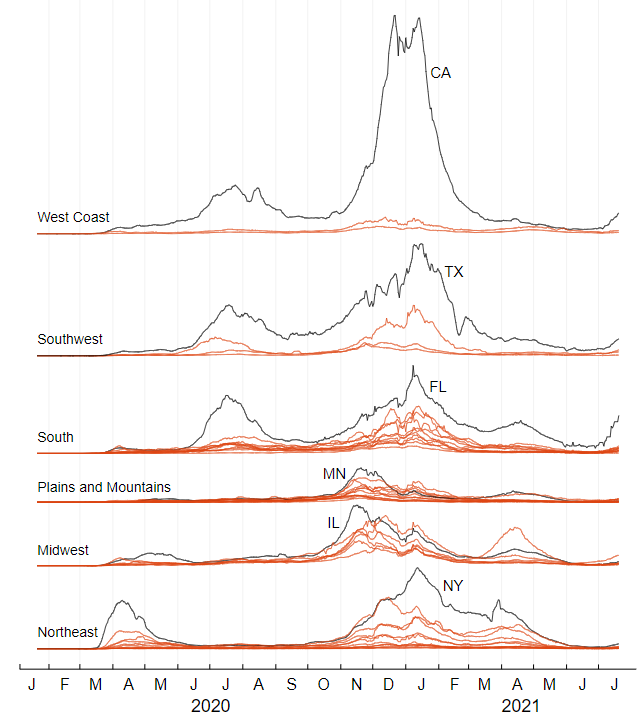
Рисунок 22

Хотя эти кривые разрушают привлекательную для меня гипотезу, в тоже время они раскрывают интересные факты об эпидемии Covid. Я знал, что первая волна была сконцентрирована в Нью-Йорке и окружающих его регионах, но не осознавал, насколько вторая волна лета 2020 года была ограничена южной частью страны, от Флориды до Калифорнии. Летняя волна 2021 года была наиболее сильной во Флориде и вдоль побережья Мексиканского залива. Совпадение? Когда я показал графики своей подруге, она ответила: «Кондиционирование воздуха».

В поисках ответа на Covid я проверил три слегка эксцентричные идеи: вероятность того, что периодический сигнал, как у цикла солнечной активности, регулярно приносит волны заражения; петли обратной связи, создающие динамику йо-йо в количестве случаев; миниэпидемии со случайным временем возникновения, складывающиеся в предсказуемую скорость заражения с небольшими отклонениями. Сейчас все они кажутся стоящими дальнейшего исследования, но ни одна из них не может убедительным образом объяснить данные.

На мой взгляд, на главные вопросы мы не получили ответа. В ноябре 2020 года общее ежедневное количество новых случаев Covid превышало 100 тысяч и росло с пугающей скоростью. Три месяца спустя скорость заражения почти столь же резко упала. Что изменилось между двумя этими датами? Какое действие, или условия, или случайность ослабили импульс нарастающей эпидемии и заставили её отступить? И как всего спустя несколько месяцев после сильного падения количества случаев мы снова поднялись выше 100 тысяч случаев в день и количество продолжает расти. Что снова изменилось и заставило эпидемию вернуться?

На эти вопросы есть пара очевидных ответов. На самом деле, эти ответы уже давно ждут, пока я упомяну их. Первый — это кампания по вакцинации, которая сегодня охватила уже половину населения США. Настоящим чудом стали невероятно быстрая разработка, производство и распространение этих вакцин. В ближайшие месяцы и годы именно они имеют шанс на наше спасение. Но непонятно, действительно ли вакцинация остановила большую волну прошлой зимой. Резкое падение скорости заражения началось в первую неделю января, когда вакцинация в США только начиналась. 9 января (дата, когда началось снижение) только 2% населения получило хотя бы одну дозу. Работа по вакцинации достигла своего пика в апреле, когда распределялось более трёх миллионов доз в день. Однако к тому времени падение количества случаев остановилось и оно снова начало расти. Если вы хотите заявить, что вакцина прекратила большой зимний всплеск, то причинность сложно увязать с хронологией.

С другой стороны, достигнутый сегодня уровень вакцинации должен был оказать мощный эффект на все последующие волны. Устранения из списка подверженных заражению половины населения может быть недостаточно для достижения коллективного иммунитета и уничтожения вируса в популяции, но его должно быть достаточно для превращения нарастающей эпидемии в затухающую.

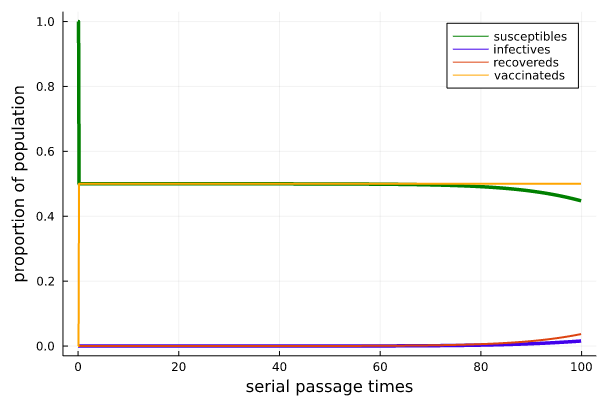
Рисунок 23

Модель SIR на Рисунке 23 имеет те же параметры, что и модель на Рисунке 3 ( $\beta = 0.6$ , $\gamma = 0.2$ ), что даёт нам $\rho = 3.0$ , но в начале симуляции вакцинировано 50% людей. При такой разбавленной популяции подверженных заражению, по сути, в течение почти года ничего не происходит. Эпидемия дремлет, но не совсем уничтожена.

Согласно модели SIR, именно в таком мире мы должны жить сегодня. Вместо этого сегодня количество случаев равно 141365; почти 81556 людей госпитализировано с заражением Covid; и 704 человека умерло. Что за дела? Как такое может происходить?

На этом моменте я должен обратить внимание на ещё один аспект: дельта-штамм, также известный как B.1.617.2. Полдюжины мутаций в белке шипа, прикрепляющегося к рецептору клеточной поверхности человека, предположительно сделали этот новый штамм по крайней мере вдвое заразнее, чем первый штамм.

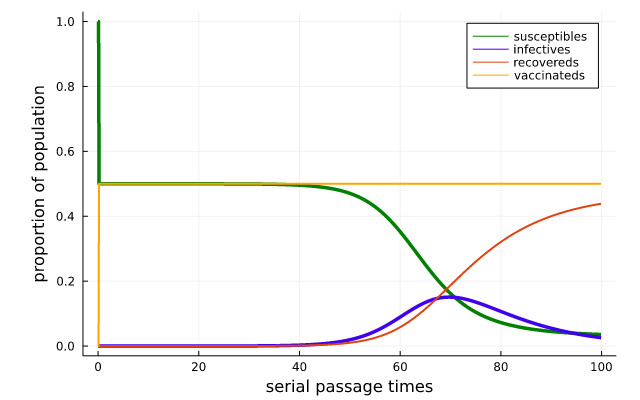
Рисунок 24

На Рисунке 24 контагиозность удвоилась из-за увеличения $\rho$ с 3,0 до 6,0. Этот скачок возродил эпидемию, хотя всё равно возникла довольно долгая задержка перед тем, как вирус широко распространился среди невакцинированной половины населения.

Ситуация может быть намного хуже, чем предсказывает модель. Все рассмотренные здесь мной модели предполагали, что популяция однородна или тщательно перемешана. Если заражённый человек будет распространять вирус, то все люди в стране имеют одинаковую вероятность стать получателями. Это допущение сильно упрощает построение модели, но, разумеется, оно далеко от истины. В повседневной жизни мы чаще всего пересекаемся с похожими на нас людьми — живущими по соседству, в той же возрастной категории, на нашем рабочем месте или в месте учёбы. Эти частые контакты также являются людьми, имеющими подобный с вами статус вакцинации. Если вы не вакцинированы, то не только более уязвимы к вирусу, но и с большей вероятностью встретитесь с его носителями. Этот довольно незначительный эффект позволил обеспечить пандемию среди невакцинированных.

Последние известия приносят ещё более пугающие и неприятные новости, свидетельства того, что даже полностью вакцинированные люди могут иногда распространять вирус. Я жду подтверждения этого, прежде чем начать паниковать. (Но жду я, надев на лицо маску.)

Продемонстрировав то, что я вообще ничего не понимаю в истории эпидемии в США — почему она росла, снижалась, росла и снова падала — я едва ли смогу понять текущий нарастающий тренд. А о будущем я вообще не имею никакого представления. Превысит ли эта новая волна все предыдущие или это последний вздох Covid? Я поверю во что угодно.

Но давайте не будем отчаиваться. Это не зомби-апокалипсис. Выживание человечества не находится под вопросом. Последние 18 месяцев были тяжёлым испытанием, и оно ещё не закончилось, но мы с ним справимся. Возможно, в какой-то момент не такого уж далёкого будущего мы даже поймём, что происходит.

Данные и исходный код

Архив данных The New York Times по случаям заражения Covid-19 и смертям в США доступен в этом репозитории GitHub. Версия, которую я использовал при подготовке этой статьи, клонированная 21 июля 2021 года, называется «commit c3ab8c1beba1f4728d284c7b1e58d7074254aff8». Вы сможете получить доступ к идентичному набору файлов по этой ссылке.

Исходный код моделей SIR и генерации иллюстраций для этой статьи тоже выложен на GitHub. Код написан на языке программирования Julia и организован в ноутбуки Pluto.

Дополнительные источники

Bartlett, M. S. 1956. Deterministic and stochastic models for recurrent epidemics. In Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability, Volume 4: Contributions to Biology and Problems of Health, pp. 81–109. Berkeley: University of California Press.

Bartlett, M. S. 1957. Measles periodicity and community size. Journal of the Royal Statistical Society, Series A (General) 120(1):48–70.

Brownlee, John. 1917. An investigation into the periodicity of measles epidemics in London from 1703 to the present day by the method 0f the periodogram. Philosophical Transactions of the Royal Society of London, Series B, 208:225–250.

Daley, D. J., and J. Gani. 1999. Epidemic Modelling: An Introduction. Cambridge: Cambridge University Press.

Kendall, David G. 1956. Deterministic and stochastic epidemics in closed populations. In Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability, Volume 4: Contributions to Biology and Problems of Health, pp. 149–165. Berkeley: University of California Press.

Kermack, W. O., and A. G. McKendrick. 1927. A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London, Series A 115:700–721.

Lloyd, Alun L. 2001. Realistic distributions of infectious periods in epidemic models: changing patterns of persistence and dynamics. Theoretical Population Biology 60:59–71.

Smith?, Robert (editor). 2014. Mathematical Modelling of Zombies. Ottawa: University of Ottawa Press.

Источник: https://habr.com/ru/post/575596/

Вернуться к списку

Интересные статьи

Вакцины COVID, их сравнение и принципы действия

Вакцин много, данных о них тоже, а что же лучше для конкретного человека ? Тема на нова, поэтому статья более аналитическая, нежели научно-популярная. Какие вакцины бываю...

# Вышел релиз GitLab 13.4 с хранилищем HashiCorp для переменных CI и Kubernetes Agent

Вышел релиз 13.4 с хранилищем HashiCorp для переменных CI, Kubernetes Agent и центром безопасности, а также переключаемыми фичами в Starter В GitLab мы всегда думаем о том, как пом...

Работа с объектным S3-хранилищем Mail.ru Cloud Solutions как с файловой системой

Waste Pickers by GabrielBStiernstrom С объектными хранилищами чаще всего работают через API. Но если очень хочется, можно сложить туда файлы и работать с ними в объектном хранилище...

На пути к построению графика

Добрый день, дорогой читатель! Эта статья возникла благодаря попытке взглянуть на операционный мониторинг со стороны аналитики. Она будет вам полезна, если: что-то из следующего списка хорош...

Алиса в стране Битрикс

Приветствую вас (лично вас, а не всех кто это читает)! Сегодня мы: Создадим приложение (навык) Алисы с использованием нового (октябрь 2019) сервиса Yandex Cloud Functions. Настроим н...