Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
На Хабре существует немало статей, посвящённых повышению производительности программ за счёт параллельных вычислений и использования векторных команд. Я решил дополнить этот список и рассказать о том, как можно оптимально задействовать все ресурсы процессора клиентской стороны веб-приложения.
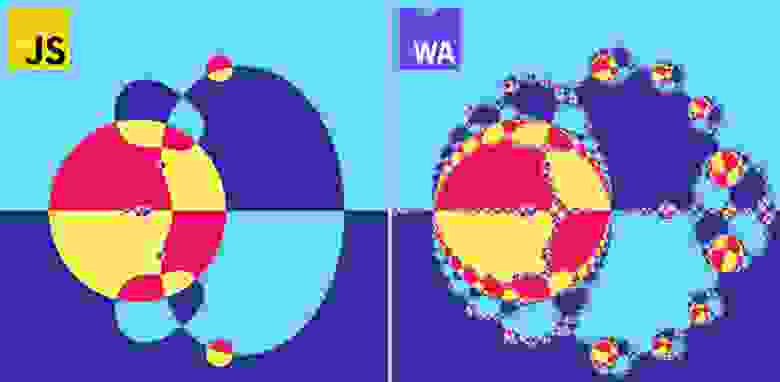
В этой части мы поговорим о том, как, используя Rust в связке с WebAssembly, можно ускорить тяжёлые вычисления на примере программы для рендеринга фрактала Ньютона. В следующей части будет подробно рассказано о векторных командах и мультипоточных вычислениях в браузере.
Прирост производительности при использовании всех техник оптимизации по сравнению с реализацией на чистом JS может составлять ~1000%: от 8–9 до 100–110 фпс. Это можно проверить на интерактивном онлайн-демо, позволяющем также поиграться с числом потоков, способом вычислений и формой фрактала.
Содержание:
- Немного про фрактал Ньютона
- Введение в WebAssembly на Rust
- Скалярная реализация фрактала Ньютона в Rust–wasm
- Сравнение скорости с реализацией в JS
- Вывод
Немного про фрактал Ньютона
Нарисовать именно его, а не какого-нибудь Мандельброта, и создать программу, задействующую для этого все ресурсы процессора, меня вдохновило видео 3blue1brown, а также его интерактивная демка фрактала (которая, впрочем, использует видеокарту для вычислений).
Фрактал Ньютона получается путём применения метода Ньютона к комплексному многочлену. Если вкратце, то метод Ньютона гласит, что чтобы найти корень функции
То есть мы можем взять любую точку
Обычно, когда говорят о комплексных числах, переменная функции обозначается символом
где
Таким образом, при разном числе итераций метода Ньютона у нас получатся следующие изображения многочлена, у которого корни расположены в вершинах равнобедренного треугольника:

Если вообще не выполнять метод Ньютона, то мы получим диаграмму Вороного
В дальнейшем мы будем пользоваться следующей упрощённой формулой метода Ньютона, пригодной только для этого случая:
Здесь:
Математическое объяснение того, почему так можно сделать
Как уже сказано ранее, наш многочлен задан в следующем виде:
По формуле метода Ньютона нам нужно найти производную от нашего многочлена, но в лоб сделать это для бесконечного произведения не получится. Поэтому воспользуемся небольшим трюком: прологарифмируем нашу функцию
нам нужно найти производную от нашего многочлена, но в лоб сделать это для бесконечного произведения не получится. Поэтому воспользуемся небольшим трюком: прологарифмируем нашу функцию
Теперь возьмём производную по , помня, что
, помня, что  :
:
И мы получили перевёрнутое искомое выражение :
:
Следовательно:
По формуле метода Ньютона
Теперь возьмём производную по
И мы получили перевёрнутое искомое выражение
Следовательно:
Введение в WebAssembly на Rust
WebAssembly — это низкоуровневый ассемблерный язык, поддерживаемый всеми современными браузерами. Главными его преимуществами являются около нативная скорость и кроссплатформенность. С его помощью можно создавать очень быстрые веб-приложения. Мы реализуем на нём функции для выполнения тяжёлых математических вычислений, а вызывать их будем через JS, где также расположим управление UI'ем.
К счастью, нам не придётся писать ассемблерный код, так как многие современные языки программирования умеют компилироваться в wasm и даже поддерживают его SIMD команды. Я выбрал Rust, поскольку он обладает подробной документацией и удобными инструментами для компилирования в wasm.
▍ Предварительная установка
Нам, само собой, потребуется установить Rust. Делается это при помощи менеджера версий rustup; ссылка на скачивание.
Также потребуется установить инструмент wasm-pack; ссылка на скачивание. Он компилирует код на Rust в WebAssembly, а также автоматически создаёт связующий слой кода на JS, который упрощает работу с функциями из wasm.
Проверить корректность установки можно с помощью консольных команд:
rustc -V и wasm-pack -V. Должны вывестись версии установленных программ.▍ Вызов wasm из JS
Попытаемся сначала скомпилировать в wasm что-то простое, например, функцию, складывающую два числа.
Создадим новый проект с помощью менеджера пакетов
cargo (который был автоматически установлен вместе с Rust) следующей консольной командой:cargo new project_nameВ директории появится папка с нашим проектом. В ней находятся 2 файла:
src/main.rs и Cargo.toml. В main.rs находится входная точка программы — функция main, выполняемая при запуске. Cargo.toml содержит всю информацию о вашем пакете: название, тип, подключённые библиотеки, параметры для компилятора и т.д. (обо всех доступных настроек можно почитать тут). Изменим в нём тип нашего проекта и подключим дополнительные пакеты, необходимые для компилирования кода под wasm:[package]
name = "project_name"
version = "0.1.0"
edition = "2021"
# Тип пакета - библиотека
[lib]
crate-type = ["cdylib"]
# Список подключённых библиотек.
# Они автоматически скачиваются\обновляются при сборке проекта.
# Никаких отдельных команд для их установки не требуется.
[dependencies]
wasm-bindgen = "0.2.63"
# wasm-bindgen - это библиотека, с помощью
# которой мы помечаем специальными аттрибутами
# те части кода, которые должны быть доступны из JS
# "0.2.63" - требуемая версия этого пакета.У каждой библиотеки входной точкой является файл
src/lib.rs, поэтому нам нужно переименовать main.rs в lib.rs.Теперь давайте создадим функцию для сложения двух чисел
sum в lib.rs:// Подключаем всё содержимое пространства имён "prelude" пакета "wasm_bindgen":
use wasm_bindgen::prelude::*;
// Аттрибут #[wasm_bindgen] используется, чтобы показать компилятору,
// что мы хотим экспортировать из wasm или импортировать из JS.
// В данном случае экспортируется функция sum, принимающая два целых числа
// и возвращающая третье число — сумму двух первых. Также, чтобы функцию
// можно было экспортировать из wasm, нужно указать префикс pub - public.
#[wasm_bindgen]
pub fn sum(a: i32, b: i32) -> i32 {
return a + b;
}В общем случае компилирование выполняется командой
wasm-pack build, но мы будем использовать её с дополнительным параметром: wasm-pack build --target web. После её выполнения в директории проекта появляется папка pkg со скомпилированном .wasm файлом, а также несколько .js и .ts файлов связующего слоя для удобного использования нашего wasm модуля.Флаг
--target управляет видом связующих JS файлов (сборки). Параметр web заставляет компилятор сделать связующий слой в виде ECMAScript модуля, позволяя импортировать wasm функции как будто из JS модуля. Полный список возможных сборок изложен тут. Мы же остановимся на web, поскольку этот способ позволяет использовать wasm без каких-либо сборщиков (webpack, nodejs и т.д.).Замечание: команда wasm-pack build может выдавать ошибку, если при пересборке не была ударена старая папка pkg.
Создадим папку www в корне проекта, а в ней index.html. Напишем в нём простой скрипт, который будет инициализировать wasm модуль и вызывать функцию сложения:
<body>
<script type="module">
// Импортируем функцию инициализации и суммирования
import init, {sum} from '../pkg/project_name.js';
async function run() {
// Инициализируем wasm модуль. Передаём путь до исходника
await init('../pkg/project_name_bg.wasm');
// Считаем и выводим в консоль сумму
let result = sum(19, 23);
console.log('result:', result);
}
run();
</script>
</body>Если вы откроете эту страничку через локальный сервер, то увидите в консоли «sum: 42». Локальный сервер нужен потому, что CORS не позволит загрузить исходный wasm файл при открытии html файла в браузере.
Скалярная реализация фрактала Ньютона в Rust–wasm
Рисование фрактала — это процесс заполнения буфера изображения. Нам нужно пробежаться по каждому пикселю, применить к нему несколько раз метод Ньютона, а потом покрасить выбранный пиксель в цвет ближайшего корня. Как обычно, начнём с простого: с реализации метода Ньютона в Rust.
Корни и точки являются комплексными числами, которые не входят в стандартные типы Rust. Чтобы не реализовывать их самим (а это подразумевает реализацию ещё нескольких математических формул), воспользуемся пакетом "num-complex". Для этого просто допишем название и версию этого пакета в разделе
[dependencies] нашего Cargo.toml:...
[dependencies]
wasm-bindgen = "0.2.63"
num-complex = "0.4.0"Теперь мы можем использовать этот пакет в нашем коде.
Нам нужна функция, которая получала бы список корней и текущую точку, а затем применяла к ней метод Ньютона и возвращала новую точку. К этому моменту наверняка большинство из читателей уже забыло, какая там была формула, поэтому я напомню:
Формула метода Ньютона
Реализуем её в новом файле
newton_method.rs в папке src:use num_complex::Complex32;
pub fn newton_method(z: Complex32, roots: &Vec<Complex32>) -> Complex32 {
let mut sum = Complex32 { re: 0.0, im: 0.0 };
for root in roots.iter() {
sum += 1.0 / (z - root);
}
return z - 1.0 / sum;
}Чтобы включить этот файл в библиотеку, нужно в главном файле (lib.rs) пометить его как модуль:
use wasm_bindgen::prelude::*;
pub mod newton_method;
...Теперь напишем функцию, которая будет выполнять этот метод N раз и возвращать id ближайшего корня:
pub fn get_root_id(mut z: Complex32, roots: &Vec<Complex32>, iterations_count: usize) -> usize {
// Выполняем метод Ньютона iterations_count раз
for _ in 0..iterations_count {
z = newton_method(z, roots);
}
// Находим ближайший к полученной точке корень
let mut min_dst = f32::MAX;
let mut min_dst_root_id: usize = 0;
for (i, root) in roots.iter().enumerate() {
let diff = z - root;
let dst = diff.norm_sqr();
if dst < min_dst {
min_dst = dst;
min_dst_root_id = i;
}
}
return min_dst_root_id;
}Однако если попробовать пометить эту функцию атрибутом
#[wasm_bindgen], то мы получим ошибку, говорящую, что для типа Complex32 не реализовано несколько ключевых для wasm_bindgen типажей (трейтов). Дело в том, что wasm_bindgen умеет работать только с базовыми типами, а для всех остальных нужно самим реализовывать методы для их конвертации в JS объекты. Эта проблема ведёт нас к следующему вопросу: как хранить и передавать объекты?▍ Хранение данных в wasm
Каждый инициализированный модуль WebAssembly обладает своей линейной памятью, выделенной внутри общей памяти JS приложения. Модули wasm имеют доступ только к своей памяти и не могут напрямую обращаться к памяти родительского процесса. При этом из JS можно получить доступ к любому участку памяти wasm. Если некий тип описан в wasm, то при создании его экземпляров они всегда будут помещаться в память wasm, а в JS обладать по умолчанию только одним полем — указателем на место этого объекта в памяти wasm.
Поэтому у нас есть два варианта организации хранения объектов: создавать объекты в JS и передавать их в качестве аргументов в наши wasm функции, или создавать объекты в wasm и писать дополнительный код, чтобы иметь возможность менять их из JS.
Мы пойдём по первому пути, так как, на мой взгляд, он уместен, когда речь идёт о простых и небольших объектах, чья десериализация при передаче в wasm не займёт много времени.
Замечание: я иногда буду использовать синтаксис TypeScript'а, чтобы было проще сопоставлять объекты в нетипизированном JS и типизированном Rust. У людей, знакомых с JS, но не знакомых с TS, не должно возникнуть никаких проблем.
Корень состоит из двух чисел: реальная и мнимая части комплексного числа. Цвет состоит из 4 байт: по одному на RGB каналы и ещё 1 на альфа-канал.
Создадим в JS массив для хранения корней и их цветов:
let roots: {re: number, im: number}[] = [
{re: 1, im: 1},
{re: 24, im: 42},
...
];
let rootsColors: [number, number, number, number][] = [
[R1, G1, B1, A1],
[R2, G2, B2, A2],
...
];Давайте для начала попробуем просто вывести в консоль значения и цвет корней. Объекты, описанные в JS, неизвестны в нашем wasm модуле. Они помечаются в Rust как
JsValue. Этот тип предоставляет пакет wasm_bindgen.#[wasm_bindgen]
pub fn log_roots(roots: JsValue, roots_colors: JsValue) {
// ...
}Простым путём получить какую-то информацию из JsValue нельзя — нужно сначала десериализовать его в типизированный объект. Наиболее просто сделать это, используя пакет serde. Это мощный инструмент, который умеет сериализовывать и десериализовывать объекты в практически любой формат данных (JSON, CBOR, YAML и т.д.), но нас сейчас волнует только его интеграция с wasm_bindgen. Она позволяет автоматически конвертировать JsValue в объекты, состоящие из примитивных типов. Для подключения нужно обновить наш Cargo.toml и пометить у wasm_bindgen, что нам нужна его свойство интеграции с serde:
...
[dependencies]
serde = "1.0.136"
wasm-bindgen = { version = "0.2.63", features = ["serde-serialize"] }
num-complex = "0.4.0"Используется она следующим образом:
#[wasm_bindgen]
pub fn serialization_example(integer: JsValue, string: JsValue, three_floats: JsValue) {
// Мы используем функцию into_serde, которая пытается конвертировать
// переданный объект integer в i32. Ключевое слово тут - пытается, поэтому
// функция возвращает тип Result, который может содержать, как и ошибку,
// так и удачно конвертированное значение. Пока что мы просто попробуем
// достать это значение с помощью функции unwrap, а если произойдёт
// ошибка, то программа вылетит.
let a: i32 = integer.into_serde().unwrap();
let b: String = string.into_serde().unwrap();
let c: [f32; 3] = three_floats.into_serde().unwrap();
// ...
}Пересобрав проект, можно проверить работу этой функции:
import {serialization_example} from '../pkg/project_name.js';
serialization_example(20, "cake", [2, 3.5, 1]);Если хоть один из аргументов будет не соответствовать ожидаемому десериализатором типу, то программа выдаст ошибку во время конвертации:
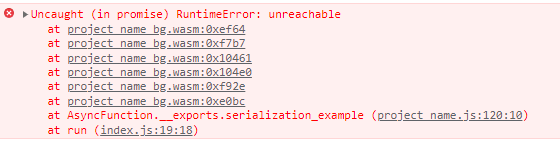
Вернёмся к нашей функции для логирования корней и попробуем сделать то же самое:
#[wasm_bindgen]
pub fn log_roots(roots: JsValue, roots_colors: JsValue) {
let roots_serialized: Vec<Complex32> = roots.into_serde().unwrap();
let roots_colors_serialized: Vec<[u8; 4]> = roots_colors.into_serde().unwrap();
}… и мы получим ошибку:
the trait bound `Complexf32: serde::de::Deserialize<'_>` is not satisfiedОна возникает из-за того, что serde не знает, как работать с типом Complex32 из библиотеки num-complex. В данный момент мы никак не можем решить эту проблему, так как в Rust нельзя расширять и изменять структуры, предоставляемые внешними пакетами. Поэтому напишем свою промежуточную структуру, в которую будем конвертировать JsValue, а потом конвертировать её в Complex32 пакета num-complex. Также, чтобы serde понимал, как работать с нашей структурой, нужно использовать макрос
#[derive(...)]. Это крайне удобный макрос, который автоматически выводит реализацию простых методов для классов, таких как вывод объекта в консоль, копирование, клонирование и т.д. Он вынесен в отдельную feature у serde и для его включения нужно немного изменить декларацию в Cargo.toml:serde = { version = "1.0.136", features = ["derive"] }Напишем свою структуру MyComplex32, пригодную для serde и конвертируемую в Complex32:
use serde::Deserialize;
// Автоматический вывод методов десериализации MyComplex
#[derive(Deserialize)]
struct MyComplex32 {
re: f32,
im: f32,
}
// Реализуем типаж Into, позволяющий конвертировать MyComplex32 в Complex32
impl Into<Complex32> for MyComplex32 {
fn into(self) -> Complex32 {
return Complex32 {
re: self.re,
im: self.im,
};
}
}Выведем в консоль браузера полученные данные. Для этого нужно подключить пакет web_sys. Это большой набор всех возможных web API, предназначенных для взаимодействия с браузером. Из-за своей масштабности каждый самостоятельный элемент web API выделен в отдельный feature. Нам пока что нужна только консоль, подключим её в нашем Cargo.toml:
web-sys = { version = "0.3.4", features = ["console"] }Теперь у нас есть доступ к функциям
web_sys::console::log(), которые выводят в консоль… снова объекты JsValue? Придётся опять подключать 100500 пакетов для выполнения сериализации? И да и нет. Проще всего выводить в веб-консоль форматированные строки, которые совсем несложно сериализировать:use web_sys::console as web_console;
// Реализуем типаж Debug, необходимый для форматирования нашей структуры в строку
#[derive(Debug)]
#[derive(Deserialize)]
struct MyComplex
...
#[wasm_bindgen]
pub fn log_roots(roots: JsValue, roots_colors: JsValue) {
let roots_serialized: Vec<MyComplex32> = roots.into_serde().unwrap();
let roots_colors_serialized: Vec<[u8; 4]> = roots_colors.into_serde().unwrap();
// Используем встроенный в Rust макрос format!, который умеет красиво форматировать строки
let msg = format!("roots: {:?}\nroots colors: {:?}", roots_serialized, roots_colors_serialized);
web_console::log_1(&msg.into());
}Если вызвать эту функцию из JS:
import {log_roots} from '../pkg/project_name.js';
let roots = [ {re: 1, im: 1}, {re: 24, im: 42} ];
let rootsColors = [ [1, 2, 3, 255], [5, 7, 11, 255] ];
log_roots(roots, rootsColors);То в консоли мы увидим следующее:

▍ Трансформация точек
Прежде чем мы займёмся заполнением буфера изображения, нам нужно решить ещё одну сугубо математическую задачку. Пиксели на картинке имеют целые координаты, лежащие в диапазоне от 0 до какой-то константы, обозначающей ширину или высоту. Точки на математическом графике фрактала, в свою очередь, могут лежать в совершенно любом промежутке. А так как мы бы хотели, чтобы фрактал можно было двигать и масштабировать, требуется написать функцию, которая бы трансформировала координаты из пространства изображения в пространство фрактала.
Для начала создадим объект, в котором будем хранить настройки размеров наших пространств. Создадим отдельный файл
geometry.rs:use wasm_bindgen::prelude::*;
#[wasm_bindgen]
pub struct PlotScale {
pub width: f32,
pub height: f32,
pub x_offset: f32,
pub y_offset: f32,
pub x_display_range: f32,
pub y_display_range: f32,
}
#[wasm_bindgen]
impl PlotScale {
// Конструктор, который в JS можно использовать через оператор new
#[wasm_bindgen(constructor)]
pub fn new(
width: f32,
height: f32,
x_offset: f32,
y_offset: f32,
x_value_range: f32,
y_value_range: f32,
) -> PlotScale {
return PlotScale { width, height, x_offset, y_offset, x_value_range, y_value_range };
}
}И не забудем подключить его в lib.rs:
pub mod geometry;
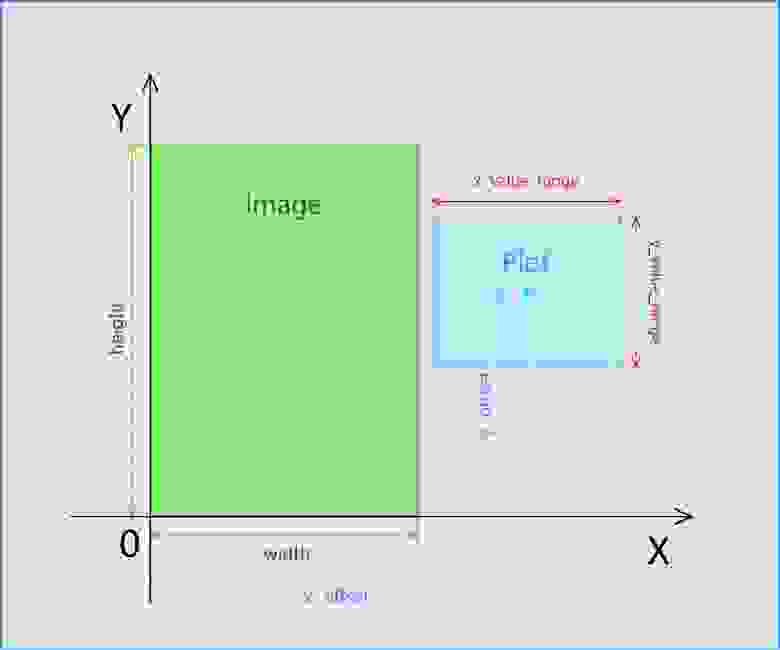
pub mod newton_method;Параметры width и height — это ширина и высота изображения.
x_offset и y_offset — смещение начала координат графика фрактала.
x_value_range и y_value_range — область допустимых значений графика фрактала.
Схематически параметры выглядят так:
Не буду нагружать статью ещё больше математикой, а сразу приведу готовые формулы для трансформации координат точек из одного пространства в другое и обратно:
// Из изображения в график
pub fn transform_point_to_plot_scale(x: f32, y: f32, plot_scale: &PlotScale) -> (f32, f32) {
(
plot_scale.x_offset + x * plot_scale.x_value_range / plot_scale.width,
plot_scale.y_offset + y * plot_scale.y_value_range / plot_scale.height,
)
}
// Из графика в изображение
pub fn transform_point_to_canvas_scale(x: f32, y: f32, plot_scale: &PlotScale) -> (f32, f32) {
(
((x - plot_scale.x_offset) * plot_scale.width / plot_scale.x_value_range),
((y - plot_scale.y_offset) * plot_scale.height / plot_scale.y_value_range),
)
}▍ Заполнение буфера изображения
Самый быстрый способ заполнить буфер изображения — это создать его прямо в памяти wasm и там же заполнить, а потом вернуть в JS указатель на него. Как уже сказано ранее, js имеет свободный доступ ко всей памяти wasm модуля, поэтому мы сможем легко создать ImageData на основе этого буфера.
Предупреждение! Дальше пойдёт небезопасный код с ручным выделением и удалением памяти.
Сначала напишем небольшой менеджер памяти
memory_management.rs (и подключим его в lib.rs). Он будет уметь создавать буфер для хранения массива u32, удалять его, а также давать доступ к памяти wasm модуля:use std::alloc::{alloc, dealloc, Layout};
use wasm_bindgen::prelude::*;
// Возвращение указателя на память wasm модуля
#[wasm_bindgen]
pub fn get_wasm_memory() -> JsValue {
wasm_bindgen::memory()
}
// Создание буфера в памяти wasm модуля
#[wasm_bindgen]
pub fn create_u32_buffer(size: usize) -> Option<u32> {
// log!("Creating buffer with {} u32 items", size);
let layout = match Layout::array::<u32>(size) {
Ok(v) => v,
Err(e) => {
log!(
"Error creating layout for u32 array of {} items: {:?}",
size,
&e
);
return None;
}
};
let buffer_ptr = unsafe { alloc(layout) } as *mut u32;
Some(buffer_ptr as u32)
}
// Освобождение памяти в wasm модуле
#[wasm_bindgen]
pub fn free_u32_buffer(size: usize, buffer_ptr: *mut u32) {
match Layout::array::<u32>(size) {
Ok(layout) => unsafe {
dealloc(buffer_ptr as *mut u8, layout);
},
Err(e) => {
log!(
"MEMORY LEAK: Error creating dealloc layout for array of {} items: {:?}",
size,
&e
);
}
};
}Теперь напишем функцию для генерации фрактала:
#[wasm_bindgen]
pub fn generate_fractal_image(
roots: JsValue,
roots_colors: JsValue,
plot_scale: &PlotScale,
iterations_count: usize,
) -> u32 {
let roots: Vec<Complex32> = roots
.into_serde::<Vec<MyComplex32>>() // Конвертируем в массив MyComplex32
.unwrap()
.into_iter()
.map(|z| z.into()) // Конвертируем MyComplex32 в Complex32
.collect();
let roots_colors: Vec<[u8; 4]> = roots_colors.into_serde().unwrap();
let &PlotScale { width, height, .. } = plot_scale;
let (width, height) = (width as usize, height as usize);
let length = width * height;
// Выделяем неуправляемую память для хранения значений пикселей
let image_data = create_u32_buffer(length) as *mut [u8; 4];
for i in 0..length {
// Вычленяем двумерные координаты из одномерного обхода
let x = i % width;
let y = i / width;
let (re, im) = transform_point_to_plot_scale(x as f32, y as f32, &plot_scale);
let z = Complex32 { re, im };
let root_id = get_root_id(z, &roots, iterations_count);
unsafe {
// Заполняем буфер изображения по указателю
// Кол-во цветов должно обязательно совпадать с кол-вом корней!
*image_data.add(i) = roots_colors[root_id];
}
}
// Возвращаем ссылку на созданный буфер
return image_data;
}Попробуем отобразить треугольный фрактал, как в гифке в начале статьи, при 5 итерациях на canvas:
import init, { get_wasm_memory, generate_fractal_image, PlotScale } from '../pkg/project_name.js';
const WIDTH = 500;
const HEIGHT = 500;
const LENGTH = WIDTH * HEIGHT;
async function run() {
await init('../pkg/project_name_bg.wasm');
// Линейная память wasm модуля
let memory = get_wasm_memory();
// Параметры отображения фрактала
let plotScale = new PlotScale(WIDTH, HEIGHT, -2, -2, 4, 4);
let canvas = document.getElementById("canvas1");
canvas.width = WIDTH;
canvas.height = HEIGHT;
let canvasCtx = canvas.getContext("2d");
const SQRT_3_DIV_2 = Math.sqrt(3) / 2;
let roots = [
{ re: 0, im: 1 },
{ re: SQRT_3_DIV_2, im: -0.5 },
{ re: -SQRT_3_DIV_2, im: -0.5 },
];
let rootsColors = [
[77, 59, 150, 255],
[110, 190, 109, 255],
[223, 106, 85, 255],
];
// Создаём и заполняем буфер изображения
let ptr = generate_fractal_image(roots, rootsColors, plotScale, 5);
// Создаём на его основе массив байт из памяти wasm
// Так как изначально у нас был массив uint32, а мы
// создаём массив uint8, необходимо увеличить длину в 4 раза
let imageBuffer = new Uint8ClampedArray(memory.buffer, ptr, 4 * LENGTH);
let imageData = new ImageData(imageBuffer, WIDTH, HEIGHT);
canvasCtx.putImageData(imageData, 0, 0);
}
run();В случае успеха должна появиться такая картинка:

Видна какая-то аномалия в районе второго и третьего корня: области покрашены в цвет первого! Если попробовать увеличить кол-во шагов, то они разрастутся.
Увеличенные области


Природа этих аномалий достаточно проста: точки, находящиеся внутри них, слишком быстро достигают корней при использовании метода Ньютона, из-за чего расстояние до корней становится равным нулю. А дальше в коде мы пытаемся поделить точку на нулевое расстояние, из-за чего вылезают NaN. Они «отменяют» все последующие математические операции, включая поиск ближайшего корня. Поэтому функция поиска корня всегда возвращает номер корня по умолчанию, который у нас равен 0
let mut min_dst_root_id: usize = 0;, а вместе с ним мы получаем синий цвет. Это легко можно проверить, заменив id корня по умолчанию на 1 или 2 — тогда мы получим зелёные и красные аномальные области соответственно.Чтобы исправить этот баг, нам нужно ввести минимальное расстояние между точкой и корнем, при достижении которого цикл будет прерываться:
const MIN_DIFF: f32 = 0.001;
pub fn newton_method(z: Complex32, roots: &Vec<Complex32>) -> Complex32 {
let mut sum = Complex32 { re: 0.0, im: 0.0 };
for root in roots.iter() {
let diff = z - root;
if diff.norm_sqr().sqrt() < MIN_DIFF {
return z;
}
sum += 1.0 / diff;
}
return z - 1.0 / sum;
}В результате аномальные области исчезнут:

Осталась одна небольшая загвоздка: память с каждым вызовом загрязняется. Если вы попробуете порисовать фрактал много раз и при этом будете выводить значение указателя на буфер, то увидите, что оно с каждой отрисовкой растёт:
И при продолжительном рисовании у вас рано или поздно закончится память, с чем вас радостно поздравит такая ошибка:

Чтобы этого не происходило, нужно чистить буфер после каждой отрисовки:
import init, { generate_fractal_image, free_u32_buffer} from '../pkg/project_name.js';
let ptr = generate_fractal_image(roots, rootsColors, plotScale, 5);
let imageBuffer = new Uint8ClampedArray(memory.buffer, ptr, 4 * LENGTH);
let imageData = new ImageData(imageBuffer, WIDTH, HEIGHT);
canvasCtx.putImageData(imageData, 0, 0);
// Чистка памяти
free_u32_buffer(ptr, LENGTH);▍ Оптимизация
Наш алгоритм можно немного улучшить. Во-первых, можно упростить математические вычисления в функции
newton_method, появившиеся при добавлении проверки на минимальное расстояние. Сейчас она выглядит так:let diff = z - root;
if diff.norm_sqr().sqrt() < MIN_DIFF {
return z;
}
sum += 1.0 / diff;Мы использовали для проверки расстояния между точками знакомую всем со школы формулу:
Убираем вызов метода sqrt():
if diff.norm_sqr() < MIN_DIFF {
return z;
}Также, если изучить формулы деления комплексных чисел, можно заметить ещё одну оптимизацию:
let mut diff = z - root;
// square_norm = x^2 + y^2
let square_norm = diff.norm_sqr();
if square_norm < MIN_DIFF {
return z;
}
diff.re /= square_norm;
diff.im /= -square_norm;
sum += diff;Она вовлекает в себя немного математики, поэтому я вынес объяснение в спойлер:
Деление комплексных чисел
Как известно, комплексные числа записываются в виде  , где i =
, где i =  — мнимая единица. Деление одного комплексного числа на другое выполняется следующим образом:
— мнимая единица. Деление одного комплексного числа на другое выполняется следующим образом:
В нашем случае мы просто инвертируем числа, поэтому . Подставим и получим:
. Подставим и получим:
А — это norm_sqr. Поэтому, чтобы инвертировать комплексное число, надо посчитать его норму, поделить реальную часть на неё, а мнимую — на её отрицательное значение:
— это norm_sqr. Поэтому, чтобы инвертировать комплексное число, надо посчитать его норму, поделить реальную часть на неё, а мнимую — на её отрицательное значение:
В нашем случае мы просто инвертируем числа, поэтому
А
let square_norm = diff.norm_sqr();
diff.re /= square_norm;
diff.im /= -square_norm;Во-вторых, в функции
newton_method мы возвращаем саму точку, если она оказалась в критической близости к одному из корней. Но, если точка оказалась близка к какому-то корню, значит, эту точку нужно покрасить в цвет этого корня. Соответственно, мы можем сразу же возвращать номер корня. Для этого удалим функцию newton_method и перенесём её в get_root_id:pub fn get_root_id(mut z: Complex32, roots: &Vec<Complex32>, iterations_count: usize) -> usize {
for _ in 0..iterations_count {
// Тело удалённой функции newton_method
let mut sum = Complex32 { re: 0.0, im: 0.0 };
for (i, root) in roots.iter().enumerate() {
let mut diff = z - root;
let square_norm = diff.norm_sqr();
if square_norm < MIN_DIFF {
// Возвращаем номер текущего корня,
// если точка оказалась рядом с ним
return z;
}
diff.re /= square_norm;
diff.im /= -square_norm;
sum += diff;
}
z -= 1.0 / sum;
}
let mut min_dst = f32::MAX;
let mut min_dst_root_id: usize = 0;
for (i, root) in roots.iter().enumerate() {
let diff = z - root;
let dst = diff.norm_sqr();
if dst < min_dst {
min_dst = dst;
min_dst_root_id = i;
}
}
return min_dst_root_id;
}Прирост производительности на моём компьютере от этих двух оптимизаций составил около 80%: при рендере того же самого «треугольного» фрактала разрешением 800х800 px с 30-ю итерациями FPS поднялся с 8.5 до 15.4.
Сравнение скорости с реализацией в JS
Моя первоначальная реализация фрактала Ньютона в JS представляла собой, по сути, трансляцию кода из Rust, поэтому она была неоптимизрована, и в первоначальном демо у wasm можно было наблюдать ускорение в 16 раз по сравнению с JS. К счастью, на реддите мне помогли оптимизировать JS реализацию, и в итоге у меня получился следующий код:
Оптимизированная реализация рендеринга фрактала в JS (TS)
type Complex = {
re: number;
im: number;
};
function calculateSquareNorm(x: number, y: number) {
return x * x + y * y;
}
function getRootId(roots: Complex[], z: Complex, iterationsCount: number) {
let i = 0;
for (let iter = 0; iter < iterationsCount; iter++) {
let sumReal = 0;
let sumImag = 0;
i = 0;
for (const root of roots) {
let diffReal = z.re - root.re;
let diffImag = z.im - root.im;
const squareNorm = calculateSquareNorm(diffReal, diffImag);
if (squareNorm < 0.001) {
return i;
}
diffReal /= squareNorm;
diffImag /= -squareNorm;
sumReal += diffReal;
sumImag += diffImag;
i++;
}
const squareNorm = calculateSquareNorm(sumReal, sumImag);
sumReal /= squareNorm;
sumImag /= -squareNorm;
z.re -= sumReal;
z.im -= sumImag;
}
let minDistance = Infinity;
let closestRootId = 0;
i = 0;
for (const root of roots) {
let diffReal = z.re - root.re;
let diffImag = z.im - root.im;
let distanceSquared = calculateSquareNorm(diffReal, diffImag);
if (distanceSquared < minDistance) {
minDistance = distanceSquared;
closestRootId = i;
}
i++;
}
return closestRootId;
}
function transformPointToPlotScale(x: number, y: number, plotScale: PlotScale) {
return [
plotScale.x_offset + x * plotScale.x_value_range / plotScale.width,
plotScale.y_offset + y * plotScale.y_value_range / plotScale.height
];
}
function fillPixelsJavascript(buffer: ArrayBuffer, roots: Complex[], rootsColors: [number, number, number, number][], plotScale: PlotScale, iterationsCount: number, ) {
let width = Math.round(plotScale.width);
let height = Math.round(plotScale.height);
let length = width * height;
let flatColors = new Uint8Array(rootsColors.flat());
let colorPacks = new Uint32Array(flatColors.buffer);
let u32BufferView = new Uint32Array(buffer, 0);
for (let i = 0; i < length; i++) {
let [xp, yp] = transformPointToPlotScale(i % width, i / width, plotScale);
u32BufferView[i] = colorPacks[
getRootId(roots, { re: xp, im: yp }, iterationsCount)
];
}
}С ним результаты получились довольно интересными: в Chrome этот код работает намного быстрее, чем в Firefox, в среднем в 2–3 раза.
Я сравнил производительность JS и wasm при отрисовке фрактала размером 800x800 px с 20-ю итерациями в обоих браузерах. Результаты в таблице ниже:
| Браузер | JS, FPS | wasm, FPS | Прирост скорости |
| Chrome | 11.8 | 15.4 | +30% |
| Firefox | 4.2 | 15.4 | +264% |
Как видим, движок Chrome очень хорошо оптимизирует код на JS и выполняет его с достаточно близкой к нативной скорости. Для кого-то её может быть достаточно, но такая реализация по-прежнему не задействует все ресурсы процессора. В следующей части вы сможете увидеть, что использование SIMD в wasm позволяет увеличить скорость в ~3 раза в Chrome и ~7.5 раз в Firefox. Но стоит учитывать, что JS оперирует 64-битными числами с плавающей точкой, в то время как в Rust мы использовали 32-битные. В принципе, если просто поменять разрядность чисел в Rust, то скорость не изменится, однако SIMD реализация будет в 2 раза медленнее, так как станет в 2 раза меньше свободных регистров для чисел.
Вывод
В целом, если вы хотите заниматься исключительно оптимизацией алгоритма, невзирая на программные ограничения и специфику JS, стоит рассмотреть вариант переноса ресурсозатратных вычислений в wasm. Это позволит добиться консистентности в скорости работы приложения во всех современных движках браузеров, а также даст небольшой, но приятный прирост скорости. Самое сложное тут, пожалуй, настроить все необходимые для компилирования в wasm инструменты и изучить какой-нибудь пригодный для wasm высокоуровневый язык программирования.
Конец первой части. Ссылка на исходный код онлайн-демо. Дальше мы будем добиваться ещё большей производительности с помощью SIMD и мультипоточности.