Алгоритм Левенберга-Марквардта прост. Алгоритм Левенберга-Марквардта эффективен.
А еще о нем говорят, что он где-то посередине между градиентным спуском и методом Ньютона, что бы это ни значило. Ну, с методом Ньютона и его связью с градиентным спуском вроде как разобрались. Но что имеют в виду когда произносят эту глубокомысленную фразу? Попробуем слегка подразобраться.
В своих статьях товарищ Левенберг [Levenberg, K. A Method for the Solution of Certain Problems in Last Squares. Quart. Appl. Math. 1944. Vol. 2. P. 164—168.], а после него гражданин Марквардт [Marquardt, Donald (1963). «An Algorithm for Least-Squares Estimation of Nonlinear Parameters». SIAM Journal on Applied Mathematics. 11 (2): 431–441.] рассмотрели задачу наименьших квадратов, которая выглядит так:
 ,
,
которую можно записать проще в векторной форме
 .
.
А можно еще проще, полностью забив на наименьшие квадраты. Это никак не повлияет на повествование.
Итак, рассматривается задача
 .
.
Такая задача возникает настолько часто, что важность нахождения эффективного метода ее решения сложно переоценить. Но мы начнем с другого. В предыдущей статье было показано, что широко известный метод градиентного спуска, и не только он, может быть получен из следующих соображений. Допустим, что мы пришли в некоторую точку , в которой минимизируемая функция имеет значение
, в которой минимизируемая функция имеет значение  . Определим в этой точке вспомогательную функцию
. Определим в этой точке вспомогательную функцию 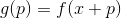 , а также некоторую ее модель
, а также некоторую ее модель 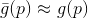 . Для данной модели мы ставим вспомогательную задачу
. Для данной модели мы ставим вспомогательную задачу

где – некоторое наперед заданное множество допустимых значений, выбираемое так, чтобы задача имела простое решение и при этом функция
– некоторое наперед заданное множество допустимых значений, выбираемое так, чтобы задача имела простое решение и при этом функция 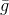 достаточно точно аппроксимировала
достаточно точно аппроксимировала  на
на  . Такую схему называют методом доверительного региона, а множество
. Такую схему называют методом доверительного региона, а множество  , на котором минимизируется значение модельной функции — доверительным регионом этой функции. Для градиентного спуска мы брали
, на котором минимизируется значение модельной функции — доверительным регионом этой функции. Для градиентного спуска мы брали  , для метода Ньютона
, для метода Ньютона  , а в качестве модели для
, а в качестве модели для  выступала линейная часть разложения в ряд Тейлора
выступала линейная часть разложения в ряд Тейлора 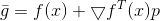 .
.
Посмотрим, что будет, если усложнить модель, взяв
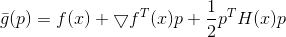 .
.
Минимизируем эту модельную функцию на эллиптическом доверительном регионе (множитель добавлен для удобства вычислений). Применив метод множителей Лагранжа, получим задачу
(множитель добавлен для удобства вычислений). Применив метод множителей Лагранжа, получим задачу
 ,
,
решение которой удовлетворяет равенству

или

Здесь, в отличие от того, что мы видели раньше при использовании линейной модели, направление p оказывается зависимым не только от метрики , но и от выбора размера доверительного региона
, но и от выбора размера доверительного региона  , а значит методика линейного поиска неприменима (по крайней мере обоснованно). Также оказывается проблемным определить в явном виде величину
, а значит методика линейного поиска неприменима (по крайней мере обоснованно). Также оказывается проблемным определить в явном виде величину  , соответствующую величине
, соответствующую величине  . Однако вполне очевидно, что при увеличении
. Однако вполне очевидно, что при увеличении  длина
длина  будет уменьшаться. Если при этом мы еще наложим условие
будет уменьшаться. Если при этом мы еще наложим условие 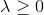 , то длина шага будет не больше, чем та, которую дал бы метод Ньютона (всамделешный, без модификаций и условий).
, то длина шага будет не больше, чем та, которую дал бы метод Ньютона (всамделешный, без модификаций и условий).
Таким образом, мы можем вместо того, чтобы для заданного искать подходящее значение
искать подходящее значение  , поступить с точностью до наоборот: найти такое
, поступить с точностью до наоборот: найти такое 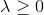 , при котором выполняется условие
, при котором выполняется условие  . Это своего рода замена почившему в данном случае линейному поиску. Марквардт предложил следующую простую процедуру:
. Это своего рода замена почившему в данном случае линейному поиску. Марквардт предложил следующую простую процедуру:
Здесь и
и  – константы, являющиеся параметрами метода. Умножение на
– константы, являющиеся параметрами метода. Умножение на  соответствует расширению доверительного региона, а умножение на
соответствует расширению доверительного региона, а умножение на  – его сужению.
– его сужению.
Указанная методика может быть применена к любой целевой функции. Заметьте, здесь уже не требуется положительная определенность гессиана в отличие от рассмотренного ранее случая, когда метод Ньютона представлялся частным случаем метода последовательного спуска. Не требуется даже его невырожденность, что в ряде случаев очень важно. Однако в этом случае увеличивается цена поиска направления, поскольку каждое изменение приводит к необходимости решать линейную систему для определения
приводит к необходимости решать линейную систему для определения  .
.
Посмотрим что будет, если применить данный подход к задаче о наименьших квадратах.
Градиент функции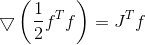 , ее гессиан
, ее гессиан 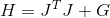 , где
, где  . Подставляем и получаем следующую систему, определяющую направление поиска
. Подставляем и получаем следующую систему, определяющую направление поиска
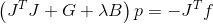 .
.
Вполне приемлемо, но вычислять вторые производные вектор-функции может быть довольно накладно. Марквардт для обхода этой проблемы предложил использовать не саму функцию , а ее линейную аппросимацию
, а ее линейную аппросимацию 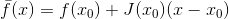 , при которой матрица
, при которой матрица  обращается в ноль. Если теперь в качестве
обращается в ноль. Если теперь в качестве  взять единичную матрицу
взять единичную матрицу 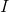 , то получим стандартную форму метода Левенберга-Марквардта для решения задачи наименьших квадратов:
, то получим стандартную форму метода Левенберга-Марквардта для решения задачи наименьших квадратов:
 .
.
Для данного способа определения направления спуска Марквардтом же была доказана теорема о том, что при устремлении к бесконечности направление
к бесконечности направление  стремится к антиградиенту. Строгое доказательство заинтересованный читатель сможет найти в базовой статье, но надеюсь, что само это утверждение стало достаточно очевидным из логики построения метода. Оно в определенной мере оправдывает вездесущую отсылку к тому, что при увеличении лямбды (которую по непонятной мне причине часто называют параметром регуляризации) мы получаем градиентный спуск. На самом деле ничего подобного — мы получили бы его только в пределе, в том самом, где длина шага стремится к нулю. Намного важнее то, что при достаточно большом значении лямбды направление, которое мы получаем, будет являться направлением спуска, а значит мы получаем глобальную сходимость метода. А вот вторая часть утверждения, что при устремлении лямбды к нулю мы получаем метод Ньютона, со всей очевидностью верна, но только если принять вместо
стремится к антиградиенту. Строгое доказательство заинтересованный читатель сможет найти в базовой статье, но надеюсь, что само это утверждение стало достаточно очевидным из логики построения метода. Оно в определенной мере оправдывает вездесущую отсылку к тому, что при увеличении лямбды (которую по непонятной мне причине часто называют параметром регуляризации) мы получаем градиентный спуск. На самом деле ничего подобного — мы получили бы его только в пределе, в том самом, где длина шага стремится к нулю. Намного важнее то, что при достаточно большом значении лямбды направление, которое мы получаем, будет являться направлением спуска, а значит мы получаем глобальную сходимость метода. А вот вторая часть утверждения, что при устремлении лямбды к нулю мы получаем метод Ньютона, со всей очевидностью верна, но только если принять вместо  ее линейную аппроксимацию
ее линейную аппроксимацию 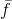 .
.
Казалось бы, всё. Минимизируем норму вектор-функции в эллиптической метрике – используем Левенберга-Марквардта. Имеем дело с функцией общего вида и имеем возможность вычислить матрицу вторых производных – велкам использовать метод доверительного региона общего вида. Но есть же извращенцы…
Иногда методом Левенберга-Марквардта для минимизации функции называют выражение вот такого вида:
называют выражение вот такого вида:
 .
.
Вроде все то же самое, но здесь – матрица вторых! производных функции
– матрица вторых! производных функции  . Формально это имеет право на существование, но является извращением. И вот почему. Тот же Марквардт в своей статье предложил метод решения системы уравнений
. Формально это имеет право на существование, но является извращением. И вот почему. Тот же Марквардт в своей статье предложил метод решения системы уравнений  путем минимизации функции
путем минимизации функции  описанным методом. Если в качестве
описанным методом. Если в качестве 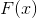 взять градиент целевой функции, то действительно получим приведенное выражение. А извращение это потому, что
взять градиент целевой функции, то действительно получим приведенное выражение. А извращение это потому, что
решается задача минимизации, порождаемая системой нелинейных уравнений, порождаемых задачей минимизации.
Даблстрайк. Такое выражение, как минимум, не лучше первого уравнения сферического доверительного региона, а вообще намного хуже как с точки зрения производительности (лишние операции по умножению, а в нормальных реализациях — факторизации), так и с точки зрения устойчивости метода (умножение матрицы на себя ухудшает ее обусловленность). Здесь иногда возражают, что гарантированно положительно определена, но в данном случае это не имеет никакого значения. Давайте посмотрим на метод Левенберга-Марквардта с позиций метода последовательного спуска. В этом случае мы, получается, хотим в качестве метрики использовать матрицу
гарантированно положительно определена, но в данном случае это не имеет никакого значения. Давайте посмотрим на метод Левенберга-Марквардта с позиций метода последовательного спуска. В этом случае мы, получается, хотим в качестве метрики использовать матрицу 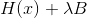 , и чтобы она могла выступать в этом качестве, значение
, и чтобы она могла выступать в этом качестве, значение  должно обеспечивать ее положительную определенность. Учитывая, что
должно обеспечивать ее положительную определенность. Учитывая, что  положительно определена, нужное значение
положительно определена, нужное значение  всегда может быть найдено — а значит никакой необходимости требовать от
всегда может быть найдено — а значит никакой необходимости требовать от  положительной определенности не наблюдается.
положительной определенности не наблюдается.
В качестве матрицы не обязательно брать единичную, но для квадратичной модели целевой функции указать адекватный доверительный регион уже не так просто, как для линейной модели. Если брать эллиптический регион, индуцированный гессианом, то метод вырождается в метод Ньютона (ну, почти)
не обязательно брать единичную, но для квадратичной модели целевой функции указать адекватный доверительный регион уже не так просто, как для линейной модели. Если брать эллиптический регион, индуцированный гессианом, то метод вырождается в метод Ньютона (ну, почти)
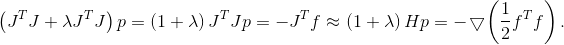
Если, конечно, матрица Гессе положительно определена. Если нет — то как и раньше можно в качестве метрики использовать исправленный гессиан, либо некоторую матрицу, к нему в каком-либо смысле близкую. Встречается также рекомендация использовать в качестве метрики матрицу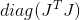 , которая по построению гарантированно является положительно определенной. К сожалению, мне не известно хоть сколь-нибудь строгого обоснования данного выбора, но в качестве эмпирической рекомендации он упоминается довольно часто.
, которая по построению гарантированно является положительно определенной. К сожалению, мне не известно хоть сколь-нибудь строгого обоснования данного выбора, но в качестве эмпирической рекомендации он упоминается довольно часто.
В качестве иллюстрации давайте посмотрим, как ведет себя метод на все той же функции Розенброка, причем мы будем рассматривать ее в двух ипостасях — как простую функцию, записанную в форме
 ,
,
и как задачу наименьших квадратов
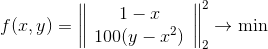

Так ведет себя метод со сферическим доверительным регионом.
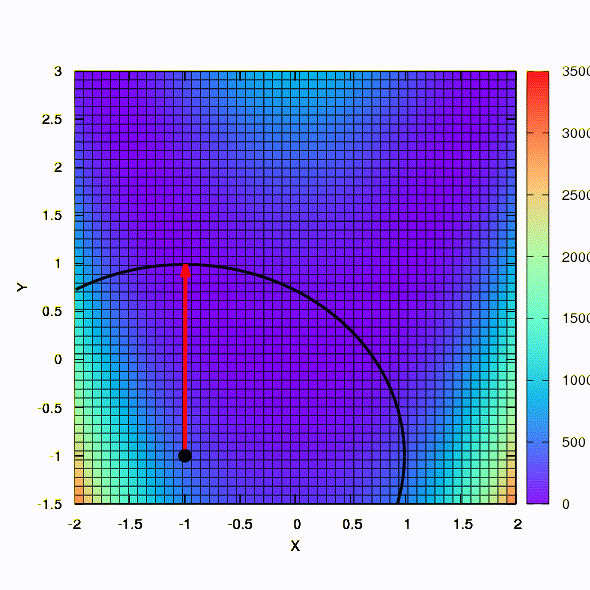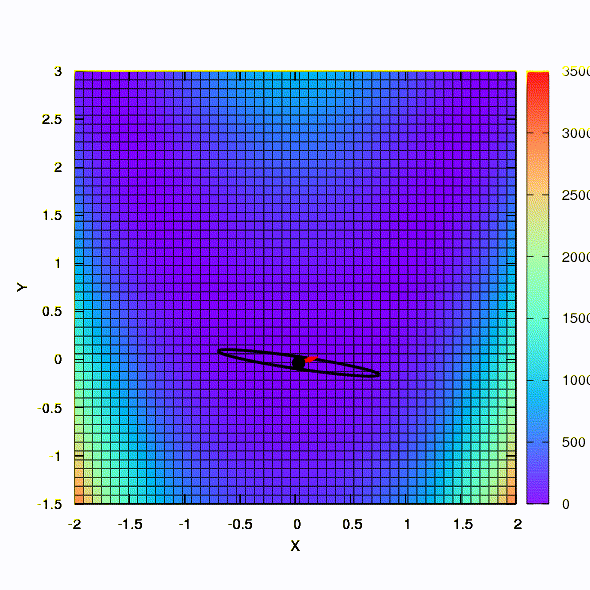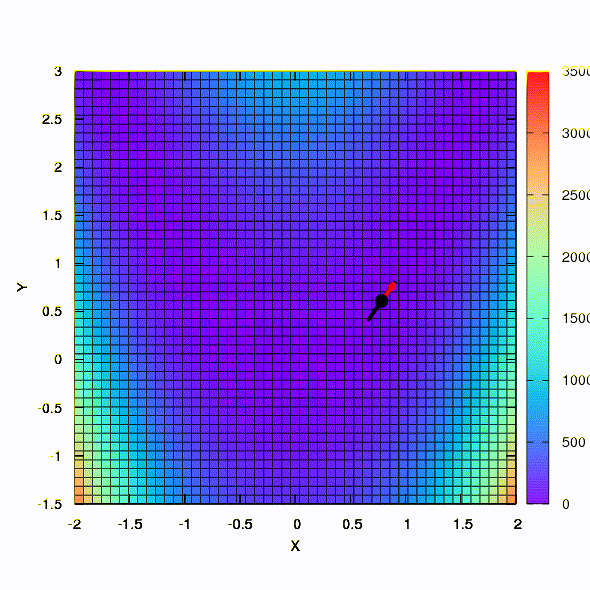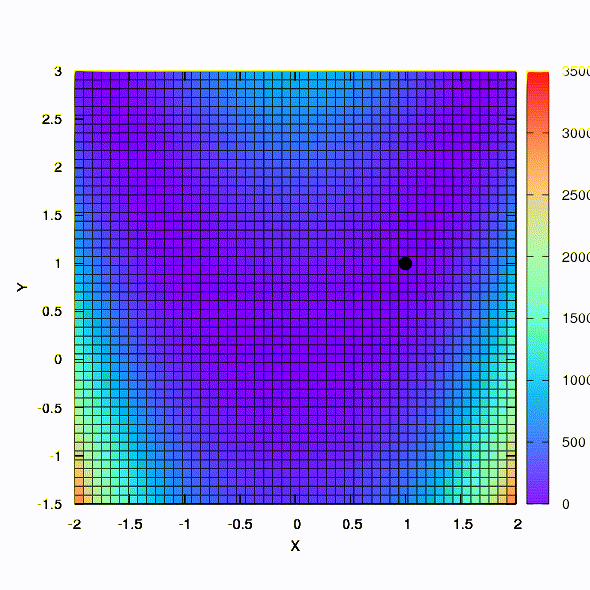
Так тот же метод ведет себя в том случае, если форма доверительного региона задается матрицей, построенной по правилу Давидона-Флетчера-Пауэла. Влияние на сходимость имеется, но куда скромнее, чем в аналогичном случае при использовании линейной модели целевой функции.
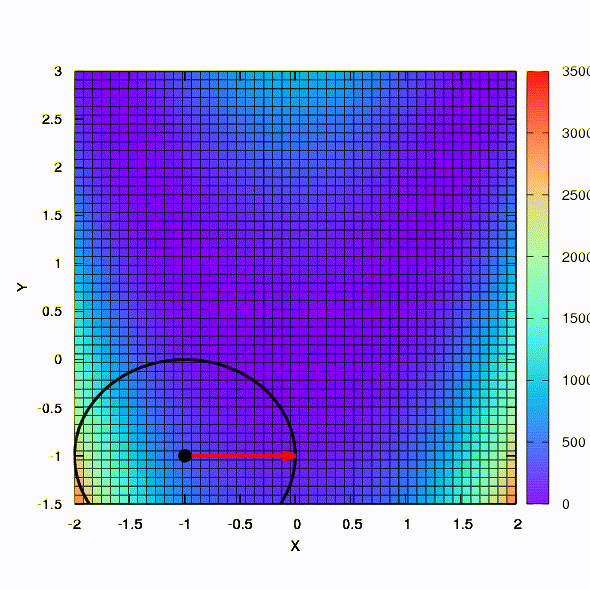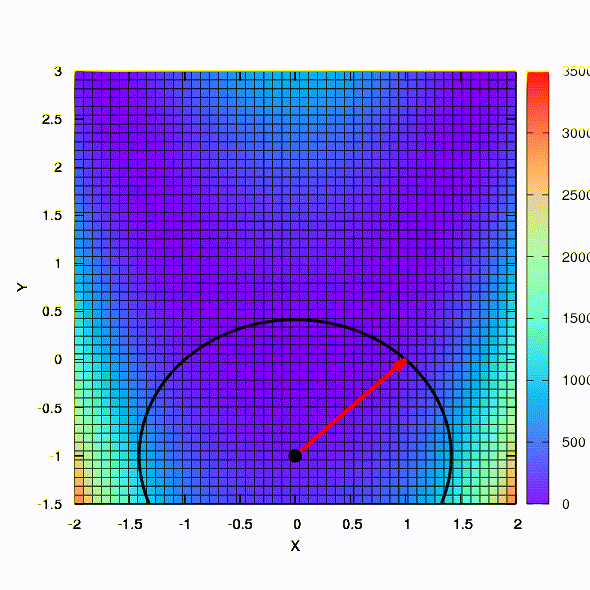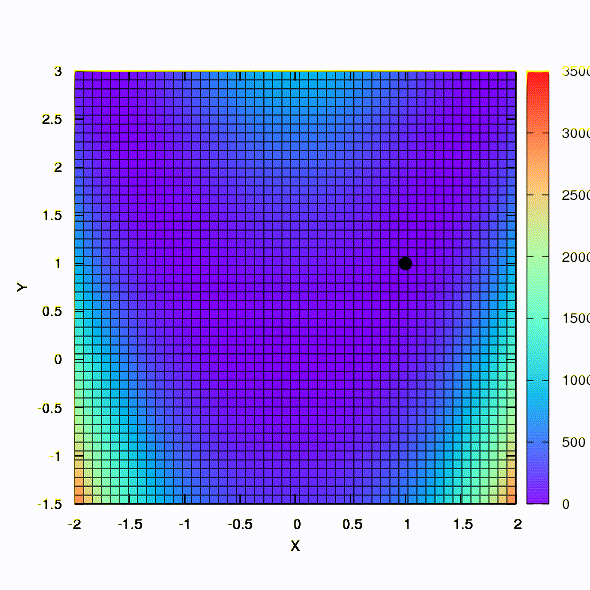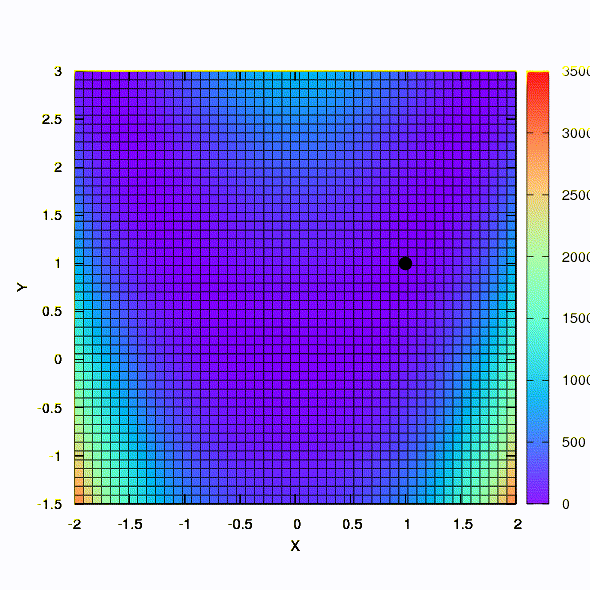
А это уже поведение метода, примененного к задаче наименьших квадратов. Сходится за 5 итераций. Только пожалуйста, не делайте из этого вывода, что вторая формулировка для функций такого вида всегда лучше первой. Это не так, просто в этом конкретном случае случае так вышло.
Метод Левенберга-Марквардта является, на сколько мне известно, первым методом, основанным на идее доверительного региона. Он весьма неплохо показал себя на практике при решении задачи наименьших квадратов. Сходится метод в большинстве случаев (виденных мной) довольно быстро (о том, хорошо это или плохо я говорил в предыдущей статье). Однако при минимизации функций общего вида выбирать сферу в качестве доверительного региона — вряд ли наилучший из возможных вариантов. Кроме того, существенным недостатком метода (в его базовой формулировке, которая здесь и была описана) является то, что размер доверительного региона задается неявно. Недостаток проявляется в том, что зная значение мы, конечно, можем в текущей точке посчитать
мы, конечно, можем в текущей точке посчитать  просто вычислив длину шага
просто вычислив длину шага  . Однако когда мы перейдем в новую точку, этому же значению
. Однако когда мы перейдем в новую точку, этому же значению  будет уже соответствовать совсем другая величина доверительного региона. Таким образом, мы лишаемся возможности определения “характерной для задачи” величины доверительного региона и вынуждены в каждой новой точке определять его размер по-новому. Это может быть существенным, когда для сходимости требуется достаточно большое количество итераций, а вычисление значения функции обходится недешево. Подобные проблемы решаются в более продвинутых методах, основанных на идее доверительного региона.
будет уже соответствовать совсем другая величина доверительного региона. Таким образом, мы лишаемся возможности определения “характерной для задачи” величины доверительного региона и вынуждены в каждой новой точке определять его размер по-новому. Это может быть существенным, когда для сходимости требуется достаточно большое количество итераций, а вычисление значения функции обходится недешево. Подобные проблемы решаются в более продвинутых методах, основанных на идее доверительного региона.
Но это уже совсем другая история.
Благодаря ценным комментариям Dark_Daiver я решил, что следует дополнить вышеизложенное следующим замечанием. Разумеется, к методу Левенберга-Марквардта можно прийти иным, чисто эмпирическим путем. А именно, вернемся к описанной в предыдущей статье схеме метода последовательного спуска и снова зададимся вопросом построения адекватной метрики для линейной модели целевой функции.
Допустим, что матрица Гессе в текущей точке поискового пространства не является положительно определенной и не может служить метрикой (причем проверить, так ли это мы не имеем ни возможности, ни желания). Обозначим за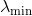 ее наименьшее собственное значение. Тогда мы можем скорректировать гессиан, просто сместив все его собственные значения на величину
ее наименьшее собственное значение. Тогда мы можем скорректировать гессиан, просто сместив все его собственные значения на величину 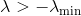 . Для этого достаточно прибавить к гессиану матрицу
. Для этого достаточно прибавить к гессиану матрицу 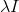 . Тогда уравнение, определяющее направление спуска, примет вид
. Тогда уравнение, определяющее направление спуска, примет вид
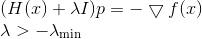
Если у нас есть хорошая оценка снизу для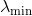 , то дальше мы можем делать все то, что делалось в методах последовательного спуска. Однако если мы такой оценки не имеем, то приняв во внимание, что при увеличении
, то дальше мы можем делать все то, что делалось в методах последовательного спуска. Однако если мы такой оценки не имеем, то приняв во внимание, что при увеличении  длина p будет уменьшаться, можно уверенно говорить о том, что найдется такое достаточно большое
длина p будет уменьшаться, можно уверенно говорить о том, что найдется такое достаточно большое  , что одновременно
, что одновременно  положительно определена и
положительно определена и  .
.
Почему такой вывод метода я считаю не слишком удачным. Во-первых, совершенно не очевидно, что построенная таким образом метрика является годной для практического применения. В ней, конечно, используется информация о вторых производных, но совершенно ни от куда не следует, что смещение собственных значений на заданную величину не сделают ее негодной. Как было отмечено коллегой в комментариях, представляется очевидным, что добавление масштабированной единичной матрицы к матрице Гессе приводит к тому, что эллиптический доверительный регион будет стремиться к сферическому и тут снова (как кажется) должны выползти проблемы застревания в каньоне и прочие прелести градиентного спуска и близких к нему методов. Но на практике такого не происходит. Мне, во всяком случае, примеров, иллюстрирующих подобное поведение наблюдать не доводилось. В таком случае возникает вопрос: а, собственно, почему?
Но такого вопроса не возникает, если смотреть на данный метод не как на частный случай методов спуска, а как на метод доверительного региона с квадратичной моделью целевой функции, поскольку ответ очевиден: при увеличении лямбды мы всего лишь сжимаем сферу — доверительный регион для нашей модели. Информация о кривизне никуда не уходит и ничем не размывается — мы всего лишь должны подобрать размер региона, в котором квадратичная модель адекватно описывает целевую функцию. Отсюда же следует, что вряд ли стоит ожидать существенного эффекта от изменения метрики, то есть формы доверительного региона, поскольку вся имеющаяся у нас информация о целевой функции и так учтена в ее модели.
Ну и во-вторых, важно при рассмотрении метода понять основную идею, приведшую Марквардта к данному методу, а именно — идею доверительного региона. Ведь в конечном счете только понимание подноготной численного метода позволит понять почему он работает и, что важнее, почему он может не работать.
А еще о нем говорят, что он где-то посередине между градиентным спуском и методом Ньютона, что бы это ни значило. Ну, с методом Ньютона и его связью с градиентным спуском вроде как разобрались. Но что имеют в виду когда произносят эту глубокомысленную фразу? Попробуем слегка подразобраться.
В своих статьях товарищ Левенберг [Levenberg, K. A Method for the Solution of Certain Problems in Last Squares. Quart. Appl. Math. 1944. Vol. 2. P. 164—168.], а после него гражданин Марквардт [Marquardt, Donald (1963). «An Algorithm for Least-Squares Estimation of Nonlinear Parameters». SIAM Journal on Applied Mathematics. 11 (2): 431–441.] рассмотрели задачу наименьших квадратов, которая выглядит так:
 ,
, которую можно записать проще в векторной форме
 .
. А можно еще проще, полностью забив на наименьшие квадраты. Это никак не повлияет на повествование.
Итак, рассматривается задача
 .
.Такая задача возникает настолько часто, что важность нахождения эффективного метода ее решения сложно переоценить. Но мы начнем с другого. В предыдущей статье было показано, что широко известный метод градиентного спуска, и не только он, может быть получен из следующих соображений. Допустим, что мы пришли в некоторую точку
 , в которой минимизируемая функция имеет значение
, в которой минимизируемая функция имеет значение  . Определим в этой точке вспомогательную функцию
. Определим в этой точке вспомогательную функцию 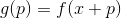 , а также некоторую ее модель
, а также некоторую ее модель 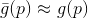 . Для данной модели мы ставим вспомогательную задачу
. Для данной модели мы ставим вспомогательную задачу 
где
 – некоторое наперед заданное множество допустимых значений, выбираемое так, чтобы задача имела простое решение и при этом функция
– некоторое наперед заданное множество допустимых значений, выбираемое так, чтобы задача имела простое решение и при этом функция 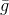 достаточно точно аппроксимировала
достаточно точно аппроксимировала  на
на  . Такую схему называют методом доверительного региона, а множество
. Такую схему называют методом доверительного региона, а множество  , на котором минимизируется значение модельной функции — доверительным регионом этой функции. Для градиентного спуска мы брали
, на котором минимизируется значение модельной функции — доверительным регионом этой функции. Для градиентного спуска мы брали  , для метода Ньютона
, для метода Ньютона  , а в качестве модели для
, а в качестве модели для  выступала линейная часть разложения в ряд Тейлора
выступала линейная часть разложения в ряд Тейлора 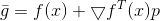 .
. Посмотрим, что будет, если усложнить модель, взяв
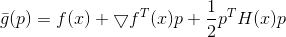 .
.Минимизируем эту модельную функцию на эллиптическом доверительном регионе
 (множитель добавлен для удобства вычислений). Применив метод множителей Лагранжа, получим задачу
(множитель добавлен для удобства вычислений). Применив метод множителей Лагранжа, получим задачу ,
,решение которой удовлетворяет равенству

или

Здесь, в отличие от того, что мы видели раньше при использовании линейной модели, направление p оказывается зависимым не только от метрики
 , но и от выбора размера доверительного региона
, но и от выбора размера доверительного региона  , а значит методика линейного поиска неприменима (по крайней мере обоснованно). Также оказывается проблемным определить в явном виде величину
, а значит методика линейного поиска неприменима (по крайней мере обоснованно). Также оказывается проблемным определить в явном виде величину  , соответствующую величине
, соответствующую величине  . Однако вполне очевидно, что при увеличении
. Однако вполне очевидно, что при увеличении  длина
длина  будет уменьшаться. Если при этом мы еще наложим условие
будет уменьшаться. Если при этом мы еще наложим условие 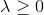 , то длина шага будет не больше, чем та, которую дал бы метод Ньютона (всамделешный, без модификаций и условий).
, то длина шага будет не больше, чем та, которую дал бы метод Ньютона (всамделешный, без модификаций и условий). Таким образом, мы можем вместо того, чтобы для заданного
 искать подходящее значение
искать подходящее значение  , поступить с точностью до наоборот: найти такое
, поступить с точностью до наоборот: найти такое 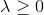 , при котором выполняется условие
, при котором выполняется условие  . Это своего рода замена почившему в данном случае линейному поиску. Марквардт предложил следующую простую процедуру:
. Это своего рода замена почившему в данном случае линейному поиску. Марквардт предложил следующую простую процедуру: - если для некотрого значения
 условие
условие 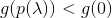 выполнено, то повторять
выполнено, то повторять  до тех пор, пока
до тех пор, пока 
- если же
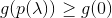 , то принять
, то принять 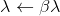 и повторить.
и повторить.
Здесь
 и
и  – константы, являющиеся параметрами метода. Умножение на
– константы, являющиеся параметрами метода. Умножение на  соответствует расширению доверительного региона, а умножение на
соответствует расширению доверительного региона, а умножение на  – его сужению.
– его сужению. Указанная методика может быть применена к любой целевой функции. Заметьте, здесь уже не требуется положительная определенность гессиана в отличие от рассмотренного ранее случая, когда метод Ньютона представлялся частным случаем метода последовательного спуска. Не требуется даже его невырожденность, что в ряде случаев очень важно. Однако в этом случае увеличивается цена поиска направления, поскольку каждое изменение
 приводит к необходимости решать линейную систему для определения
приводит к необходимости решать линейную систему для определения  .
.Посмотрим что будет, если применить данный подход к задаче о наименьших квадратах.
Градиент функции
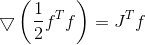 , ее гессиан
, ее гессиан 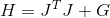 , где
, где  . Подставляем и получаем следующую систему, определяющую направление поиска
. Подставляем и получаем следующую систему, определяющую направление поиска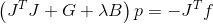 .
.Вполне приемлемо, но вычислять вторые производные вектор-функции может быть довольно накладно. Марквардт для обхода этой проблемы предложил использовать не саму функцию
 , а ее линейную аппросимацию
, а ее линейную аппросимацию 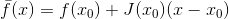 , при которой матрица
, при которой матрица  обращается в ноль. Если теперь в качестве
обращается в ноль. Если теперь в качестве  взять единичную матрицу
взять единичную матрицу 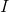 , то получим стандартную форму метода Левенберга-Марквардта для решения задачи наименьших квадратов:
, то получим стандартную форму метода Левенберга-Марквардта для решения задачи наименьших квадратов: .
.Для данного способа определения направления спуска Марквардтом же была доказана теорема о том, что при устремлении
 к бесконечности направление
к бесконечности направление  стремится к антиградиенту. Строгое доказательство заинтересованный читатель сможет найти в базовой статье, но надеюсь, что само это утверждение стало достаточно очевидным из логики построения метода. Оно в определенной мере оправдывает вездесущую отсылку к тому, что при увеличении лямбды (которую по непонятной мне причине часто называют параметром регуляризации) мы получаем градиентный спуск. На самом деле ничего подобного — мы получили бы его только в пределе, в том самом, где длина шага стремится к нулю. Намного важнее то, что при достаточно большом значении лямбды направление, которое мы получаем, будет являться направлением спуска, а значит мы получаем глобальную сходимость метода. А вот вторая часть утверждения, что при устремлении лямбды к нулю мы получаем метод Ньютона, со всей очевидностью верна, но только если принять вместо
стремится к антиградиенту. Строгое доказательство заинтересованный читатель сможет найти в базовой статье, но надеюсь, что само это утверждение стало достаточно очевидным из логики построения метода. Оно в определенной мере оправдывает вездесущую отсылку к тому, что при увеличении лямбды (которую по непонятной мне причине часто называют параметром регуляризации) мы получаем градиентный спуск. На самом деле ничего подобного — мы получили бы его только в пределе, в том самом, где длина шага стремится к нулю. Намного важнее то, что при достаточно большом значении лямбды направление, которое мы получаем, будет являться направлением спуска, а значит мы получаем глобальную сходимость метода. А вот вторая часть утверждения, что при устремлении лямбды к нулю мы получаем метод Ньютона, со всей очевидностью верна, но только если принять вместо  ее линейную аппроксимацию
ее линейную аппроксимацию 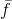 .
.Казалось бы, всё. Минимизируем норму вектор-функции в эллиптической метрике – используем Левенберга-Марквардта. Имеем дело с функцией общего вида и имеем возможность вычислить матрицу вторых производных – велкам использовать метод доверительного региона общего вида. Но есть же извращенцы…
Иногда методом Левенберга-Марквардта для минимизации функции
 называют выражение вот такого вида:
называют выражение вот такого вида: .
. Вроде все то же самое, но здесь
 – матрица вторых! производных функции
– матрица вторых! производных функции  . Формально это имеет право на существование, но является извращением. И вот почему. Тот же Марквардт в своей статье предложил метод решения системы уравнений
. Формально это имеет право на существование, но является извращением. И вот почему. Тот же Марквардт в своей статье предложил метод решения системы уравнений  путем минимизации функции
путем минимизации функции  описанным методом. Если в качестве
описанным методом. Если в качестве 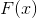 взять градиент целевой функции, то действительно получим приведенное выражение. А извращение это потому, что
взять градиент целевой функции, то действительно получим приведенное выражение. А извращение это потому, что решается задача минимизации, порождаемая системой нелинейных уравнений, порождаемых задачей минимизации.
Даблстрайк. Такое выражение, как минимум, не лучше первого уравнения сферического доверительного региона, а вообще намного хуже как с точки зрения производительности (лишние операции по умножению, а в нормальных реализациях — факторизации), так и с точки зрения устойчивости метода (умножение матрицы на себя ухудшает ее обусловленность). Здесь иногда возражают, что
 гарантированно положительно определена, но в данном случае это не имеет никакого значения. Давайте посмотрим на метод Левенберга-Марквардта с позиций метода последовательного спуска. В этом случае мы, получается, хотим в качестве метрики использовать матрицу
гарантированно положительно определена, но в данном случае это не имеет никакого значения. Давайте посмотрим на метод Левенберга-Марквардта с позиций метода последовательного спуска. В этом случае мы, получается, хотим в качестве метрики использовать матрицу 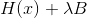 , и чтобы она могла выступать в этом качестве, значение
, и чтобы она могла выступать в этом качестве, значение  должно обеспечивать ее положительную определенность. Учитывая, что
должно обеспечивать ее положительную определенность. Учитывая, что  положительно определена, нужное значение
положительно определена, нужное значение  всегда может быть найдено — а значит никакой необходимости требовать от
всегда может быть найдено — а значит никакой необходимости требовать от  положительной определенности не наблюдается.
положительной определенности не наблюдается. В качестве матрицы
 не обязательно брать единичную, но для квадратичной модели целевой функции указать адекватный доверительный регион уже не так просто, как для линейной модели. Если брать эллиптический регион, индуцированный гессианом, то метод вырождается в метод Ньютона (ну, почти)
не обязательно брать единичную, но для квадратичной модели целевой функции указать адекватный доверительный регион уже не так просто, как для линейной модели. Если брать эллиптический регион, индуцированный гессианом, то метод вырождается в метод Ньютона (ну, почти)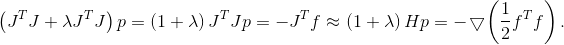
Если, конечно, матрица Гессе положительно определена. Если нет — то как и раньше можно в качестве метрики использовать исправленный гессиан, либо некоторую матрицу, к нему в каком-либо смысле близкую. Встречается также рекомендация использовать в качестве метрики матрицу
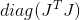 , которая по построению гарантированно является положительно определенной. К сожалению, мне не известно хоть сколь-нибудь строгого обоснования данного выбора, но в качестве эмпирической рекомендации он упоминается довольно часто.
, которая по построению гарантированно является положительно определенной. К сожалению, мне не известно хоть сколь-нибудь строгого обоснования данного выбора, но в качестве эмпирической рекомендации он упоминается довольно часто.В качестве иллюстрации давайте посмотрим, как ведет себя метод на все той же функции Розенброка, причем мы будем рассматривать ее в двух ипостасях — как простую функцию, записанную в форме
 ,
, и как задачу наименьших квадратов
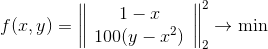

Так ведет себя метод со сферическим доверительным регионом.

Так тот же метод ведет себя в том случае, если форма доверительного региона задается матрицей, построенной по правилу Давидона-Флетчера-Пауэла. Влияние на сходимость имеется, но куда скромнее, чем в аналогичном случае при использовании линейной модели целевой функции.

А это уже поведение метода, примененного к задаче наименьших квадратов. Сходится за 5 итераций. Только пожалуйста, не делайте из этого вывода, что вторая формулировка для функций такого вида всегда лучше первой. Это не так, просто в этом конкретном случае случае так вышло.
Заключение
Метод Левенберга-Марквардта является, на сколько мне известно, первым методом, основанным на идее доверительного региона. Он весьма неплохо показал себя на практике при решении задачи наименьших квадратов. Сходится метод в большинстве случаев (виденных мной) довольно быстро (о том, хорошо это или плохо я говорил в предыдущей статье). Однако при минимизации функций общего вида выбирать сферу в качестве доверительного региона — вряд ли наилучший из возможных вариантов. Кроме того, существенным недостатком метода (в его базовой формулировке, которая здесь и была описана) является то, что размер доверительного региона задается неявно. Недостаток проявляется в том, что зная значение
 мы, конечно, можем в текущей точке посчитать
мы, конечно, можем в текущей точке посчитать  просто вычислив длину шага
просто вычислив длину шага  . Однако когда мы перейдем в новую точку, этому же значению
. Однако когда мы перейдем в новую точку, этому же значению  будет уже соответствовать совсем другая величина доверительного региона. Таким образом, мы лишаемся возможности определения “характерной для задачи” величины доверительного региона и вынуждены в каждой новой точке определять его размер по-новому. Это может быть существенным, когда для сходимости требуется достаточно большое количество итераций, а вычисление значения функции обходится недешево. Подобные проблемы решаются в более продвинутых методах, основанных на идее доверительного региона.
будет уже соответствовать совсем другая величина доверительного региона. Таким образом, мы лишаемся возможности определения “характерной для задачи” величины доверительного региона и вынуждены в каждой новой точке определять его размер по-новому. Это может быть существенным, когда для сходимости требуется достаточно большое количество итераций, а вычисление значения функции обходится недешево. Подобные проблемы решаются в более продвинутых методах, основанных на идее доверительного региона.Но это уже совсем другая история.
Дополнение
Благодаря ценным комментариям Dark_Daiver я решил, что следует дополнить вышеизложенное следующим замечанием. Разумеется, к методу Левенберга-Марквардта можно прийти иным, чисто эмпирическим путем. А именно, вернемся к описанной в предыдущей статье схеме метода последовательного спуска и снова зададимся вопросом построения адекватной метрики для линейной модели целевой функции.
Допустим, что матрица Гессе в текущей точке поискового пространства не является положительно определенной и не может служить метрикой (причем проверить, так ли это мы не имеем ни возможности, ни желания). Обозначим за
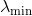 ее наименьшее собственное значение. Тогда мы можем скорректировать гессиан, просто сместив все его собственные значения на величину
ее наименьшее собственное значение. Тогда мы можем скорректировать гессиан, просто сместив все его собственные значения на величину 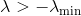 . Для этого достаточно прибавить к гессиану матрицу
. Для этого достаточно прибавить к гессиану матрицу 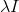 . Тогда уравнение, определяющее направление спуска, примет вид
. Тогда уравнение, определяющее направление спуска, примет вид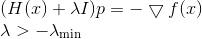
Если у нас есть хорошая оценка снизу для
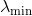 , то дальше мы можем делать все то, что делалось в методах последовательного спуска. Однако если мы такой оценки не имеем, то приняв во внимание, что при увеличении
, то дальше мы можем делать все то, что делалось в методах последовательного спуска. Однако если мы такой оценки не имеем, то приняв во внимание, что при увеличении  длина p будет уменьшаться, можно уверенно говорить о том, что найдется такое достаточно большое
длина p будет уменьшаться, можно уверенно говорить о том, что найдется такое достаточно большое  , что одновременно
, что одновременно  положительно определена и
положительно определена и  .
.Почему такой вывод метода я считаю не слишком удачным. Во-первых, совершенно не очевидно, что построенная таким образом метрика является годной для практического применения. В ней, конечно, используется информация о вторых производных, но совершенно ни от куда не следует, что смещение собственных значений на заданную величину не сделают ее негодной. Как было отмечено коллегой в комментариях, представляется очевидным, что добавление масштабированной единичной матрицы к матрице Гессе приводит к тому, что эллиптический доверительный регион будет стремиться к сферическому и тут снова (как кажется) должны выползти проблемы застревания в каньоне и прочие прелести градиентного спуска и близких к нему методов. Но на практике такого не происходит. Мне, во всяком случае, примеров, иллюстрирующих подобное поведение наблюдать не доводилось. В таком случае возникает вопрос: а, собственно, почему?
Но такого вопроса не возникает, если смотреть на данный метод не как на частный случай методов спуска, а как на метод доверительного региона с квадратичной моделью целевой функции, поскольку ответ очевиден: при увеличении лямбды мы всего лишь сжимаем сферу — доверительный регион для нашей модели. Информация о кривизне никуда не уходит и ничем не размывается — мы всего лишь должны подобрать размер региона, в котором квадратичная модель адекватно описывает целевую функцию. Отсюда же следует, что вряд ли стоит ожидать существенного эффекта от изменения метрики, то есть формы доверительного региона, поскольку вся имеющаяся у нас информация о целевой функции и так учтена в ее модели.
Ну и во-вторых, важно при рассмотрении метода понять основную идею, приведшую Марквардта к данному методу, а именно — идею доверительного региона. Ведь в конечном счете только понимание подноготной численного метода позволит понять почему он работает и, что важнее, почему он может не работать.