Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
Лучший способ объяснить школьникам и самому себе, что такое фазовое (конфигурационное) пространство.
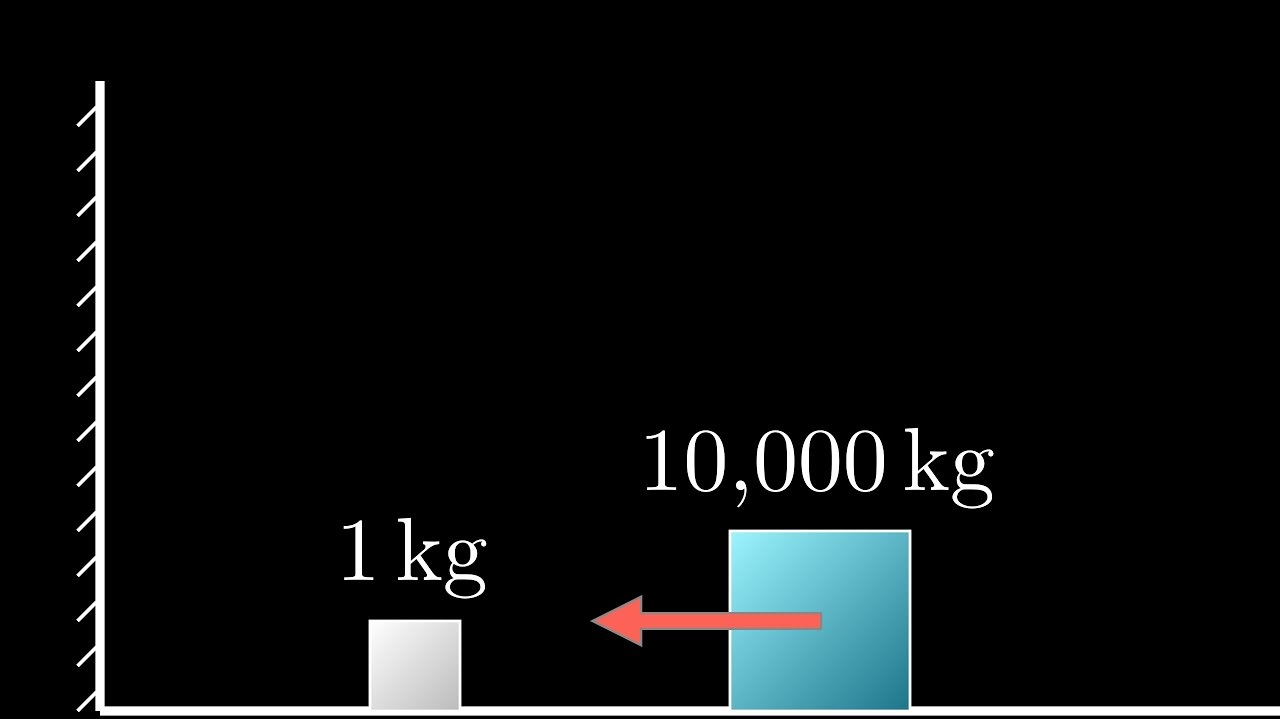
Дано: Два блока массой 1 кг и 100 (10 000, 1 000 000,… 100x) кг. Трение в системе отсутствует, удары абсолютно упругие (потерь энергии нет). Более массивный блок ударяет менее массивный и тот отскакивает от него а потом от стенки.
Вопрос: Сколько столкновений совершит маленький блок, пока система не придет в состояние, когда столкновения невозможны?
Ответ невероятен:
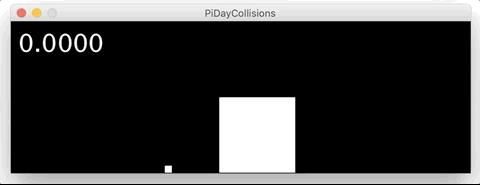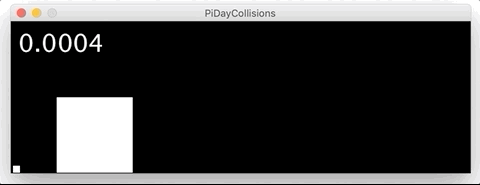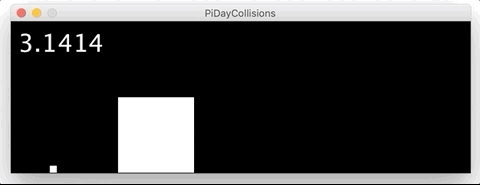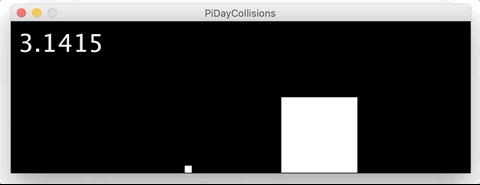
В очередной раз поражаюсь изящности объяснений от 3Blue1Brown.
В случае когда массы раны, мы насчитаем 3 столкновения:

Если разница масс в 100 раз, то количество столкновений 31:
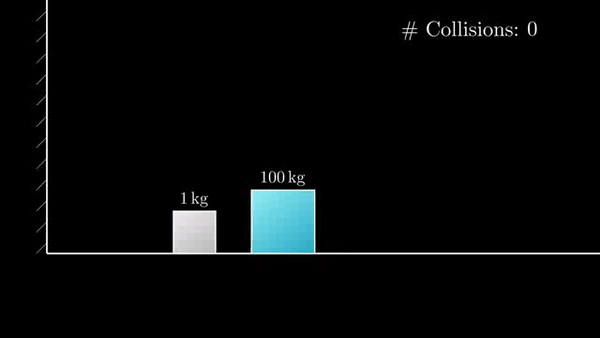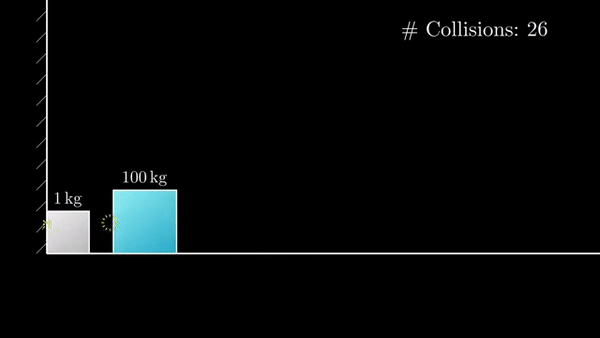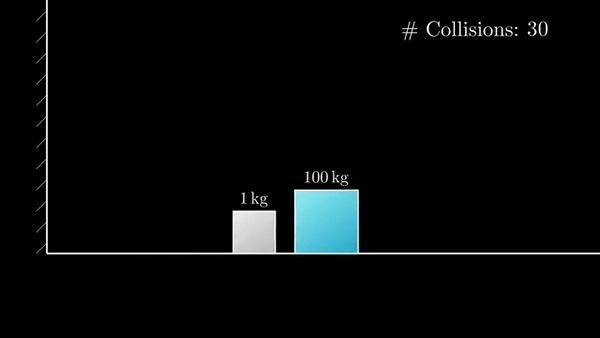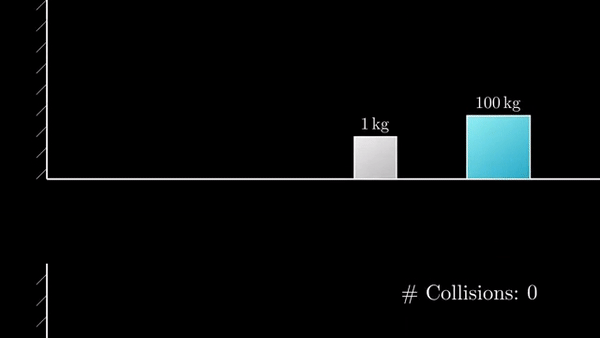
Если разница масс в 10 000 раз, то столкновений будет 314:
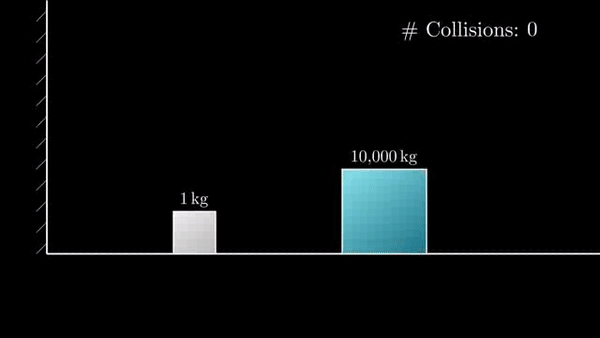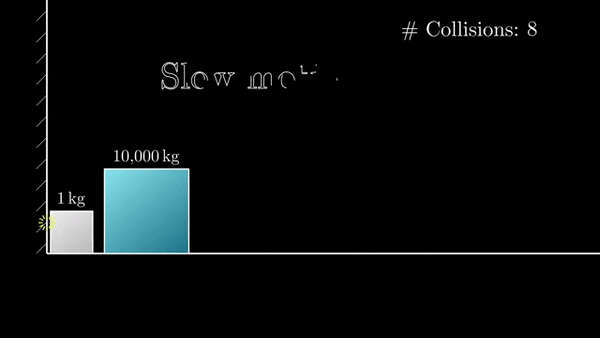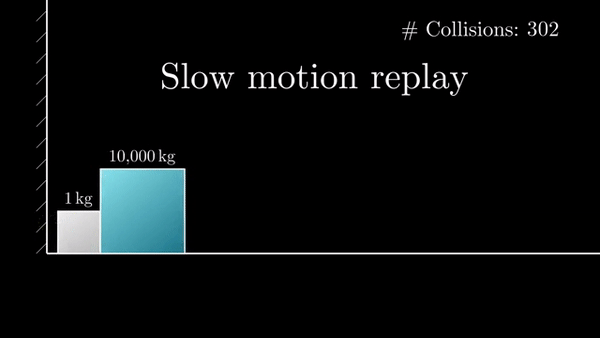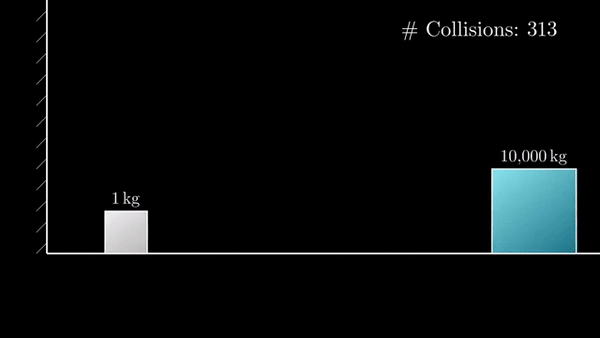
+ еще один удар об стенку
Если разница в 1 000 000 раз, то столкновений 3141:

Если разница в 100 000 000 раз, то столкновений 31415:
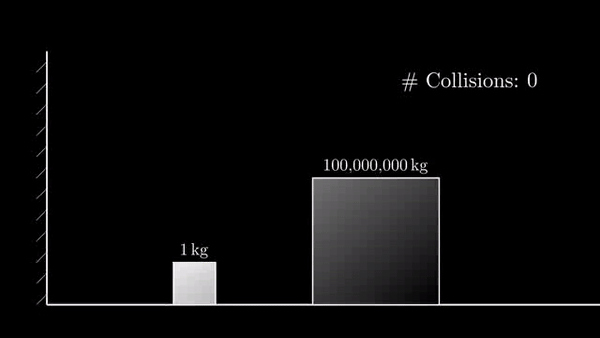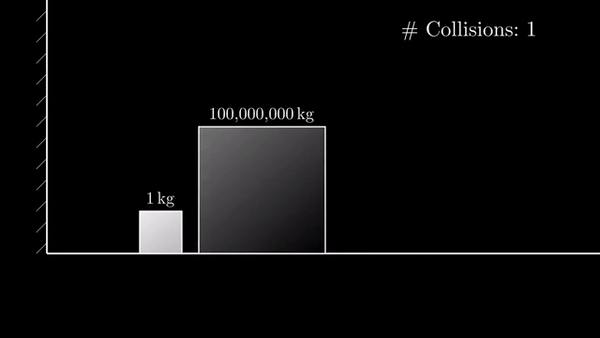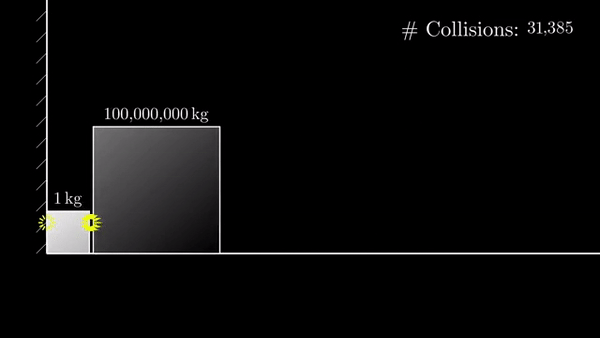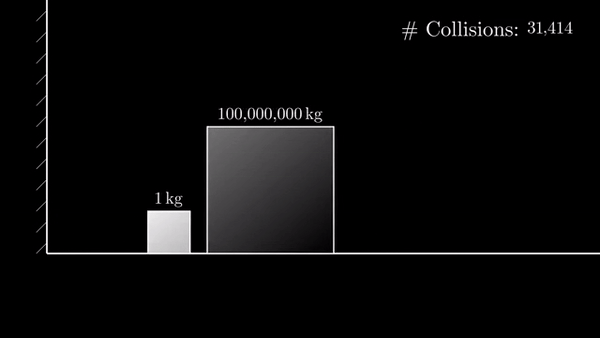
Если разница в 10 000 000 000 раз, то столкновений 314159:
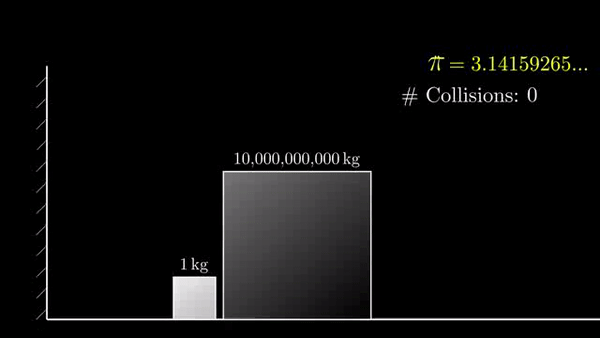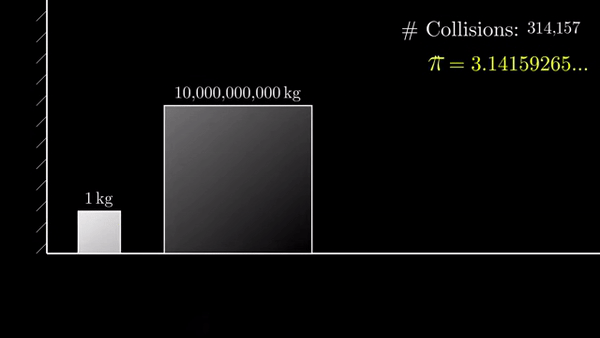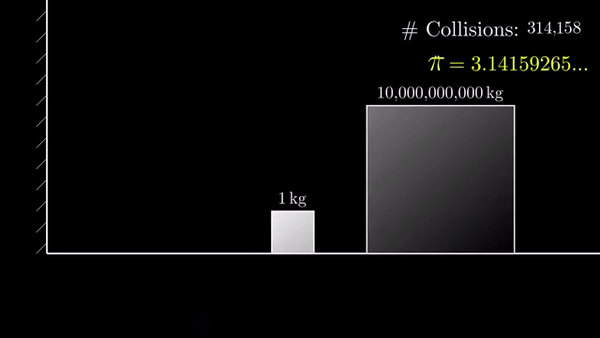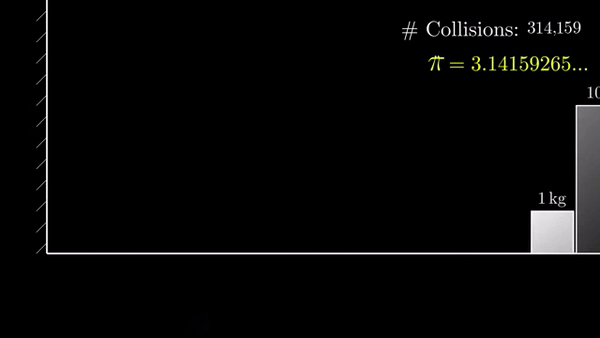
Эта закономерность была открыта Грегори Гальперином в 1995 и опубликована в 2003 году:

PLAYING POOL WITH ℼ (2003)
Данный метод позволяет построить «физическую» машину вычисления числа ℼ с точностью до n-ного знака. Разница масс должна составлять 100(n-1) раз.
С реализацией, конечно, есть нюансы, ну да ладно. Зато красивая идея.
Throwing ℼ at a wall (2006)

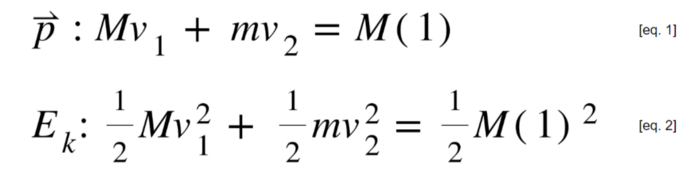
Механическая система описывается двумя законами сохранения: энергии и импульса.
Фазовое пространство для энергии системы представляет собой эллипс, но его можно откалибровать корнем из разницы масс:
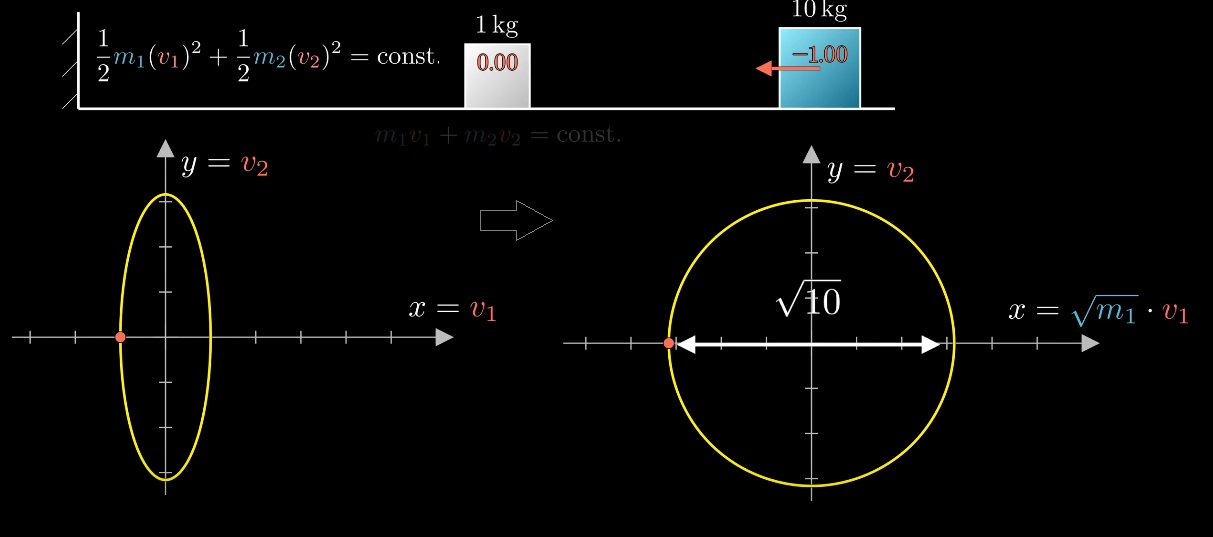
Радиус окружности показывает энергию в системе — она всегда постоянная.
При столкновении двух блоков происходит перераспределение импульса и энергии:
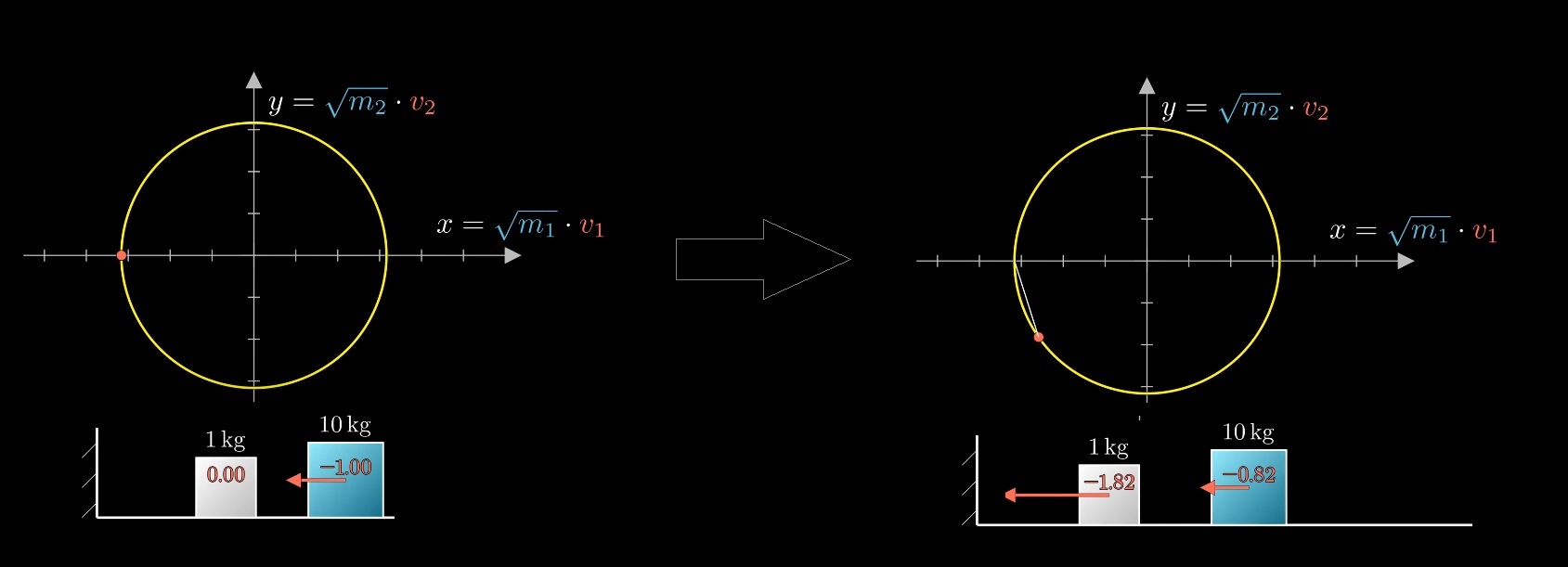
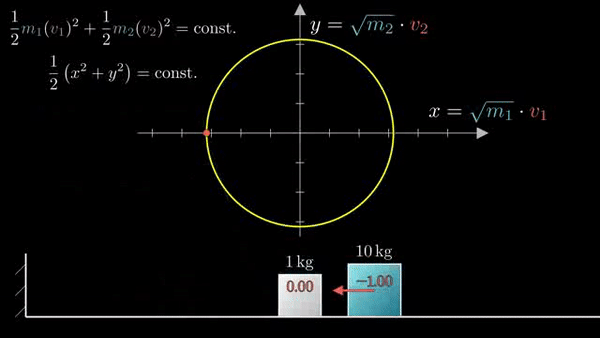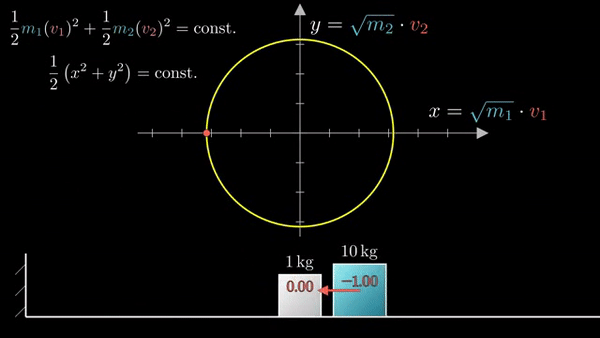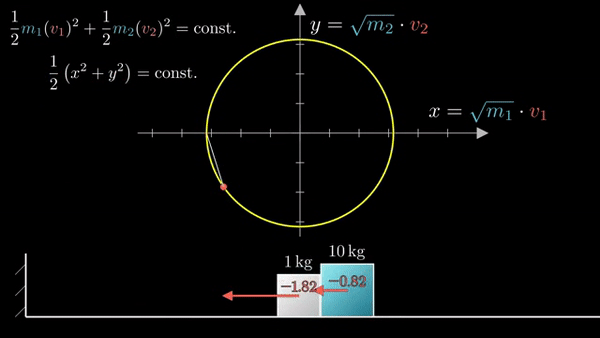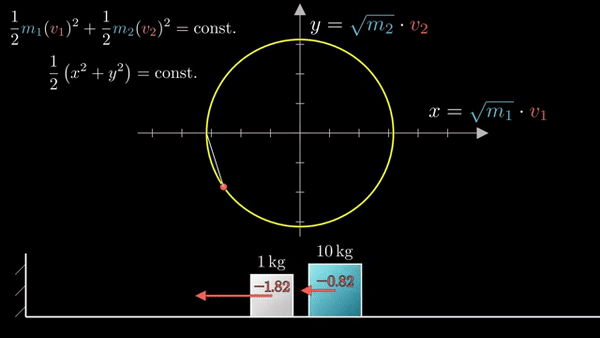
Закон сохранения моментов задает угол наклона:
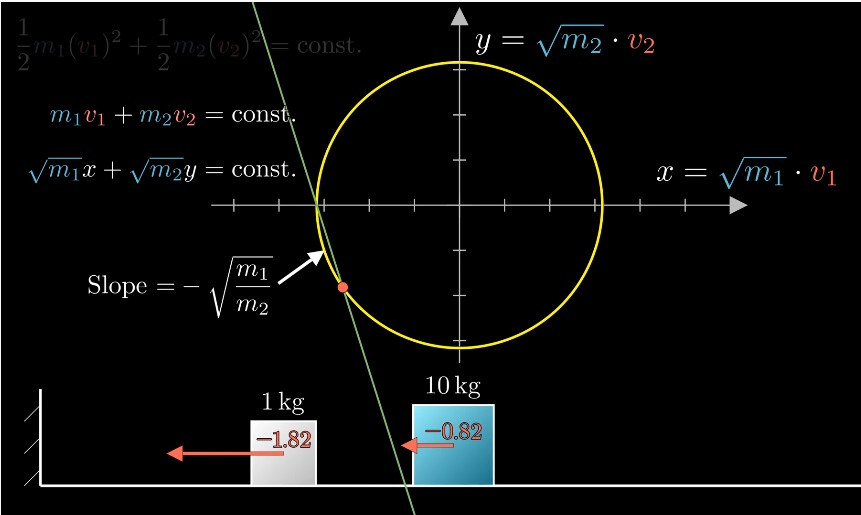
При ударе об стену (объект бесконечной массы) скорость блока меняется на противоположную:

Следующее соударение блоков:
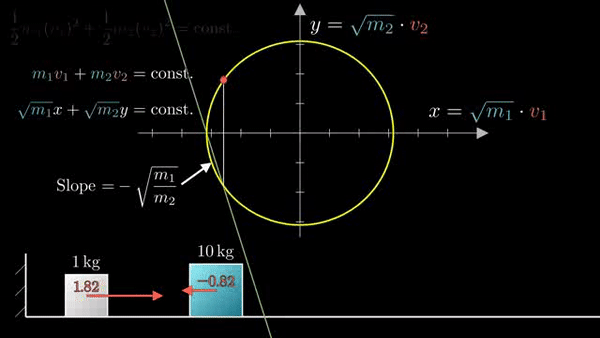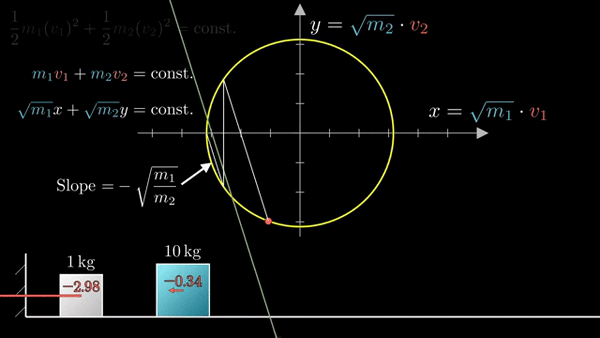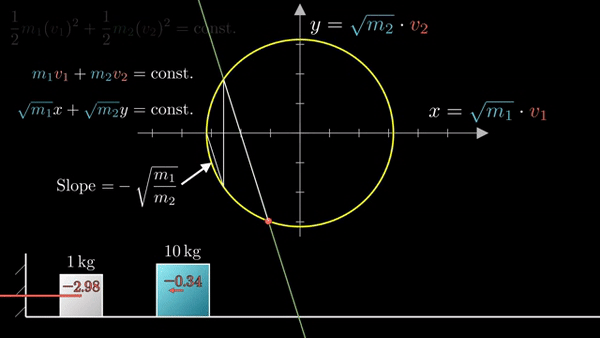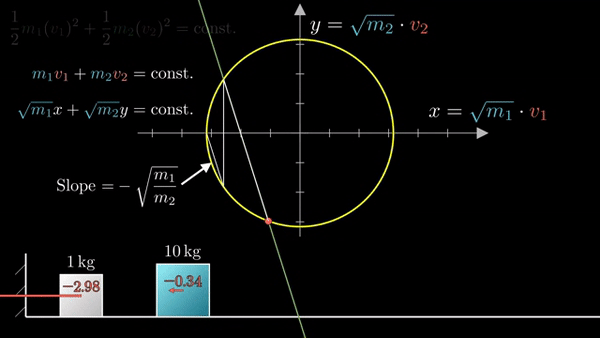
Последующие столкновения:
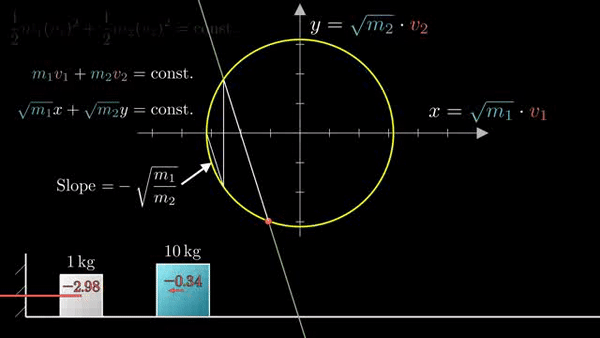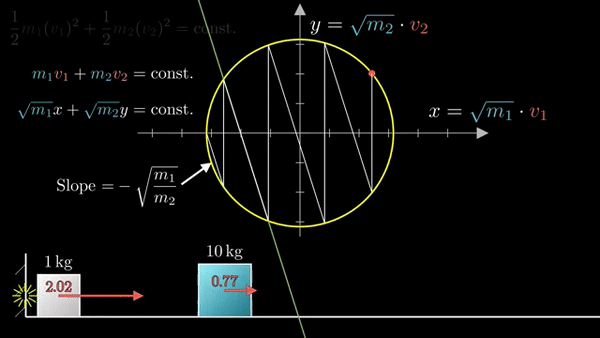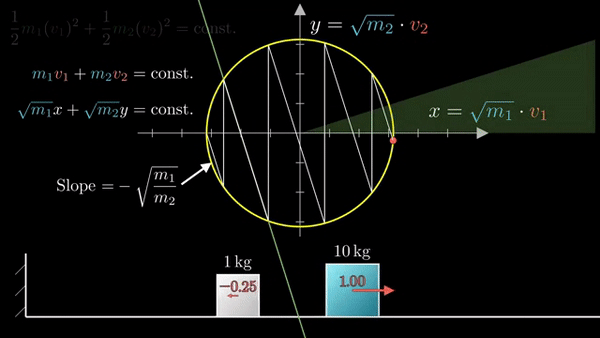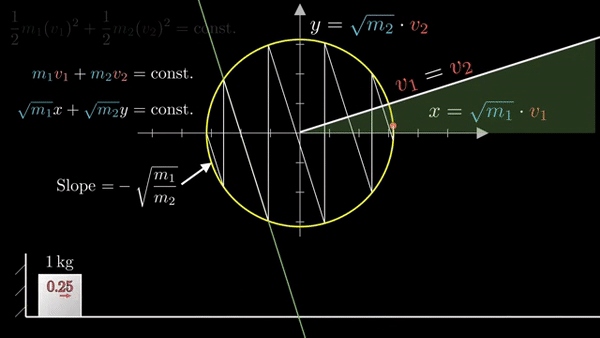
Фазовая диаграмма удобна тем, что наглядно кодирует состояние системы:
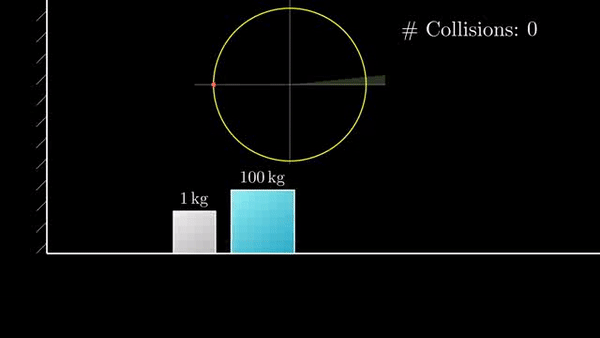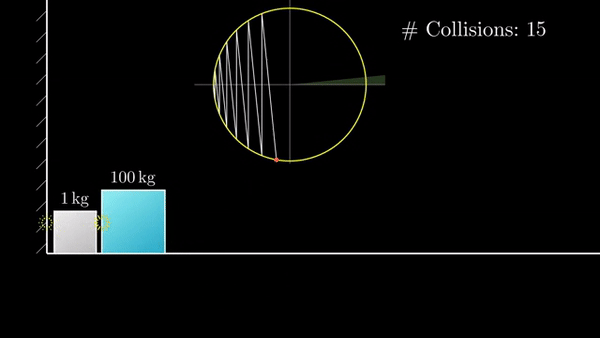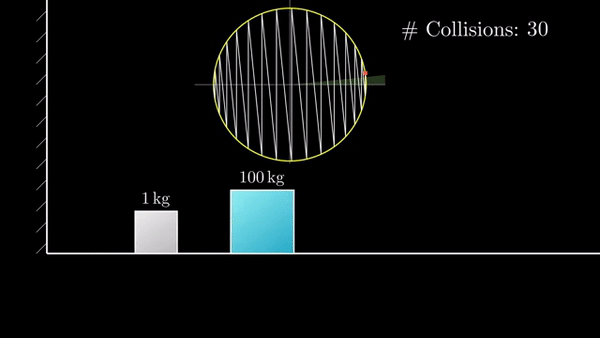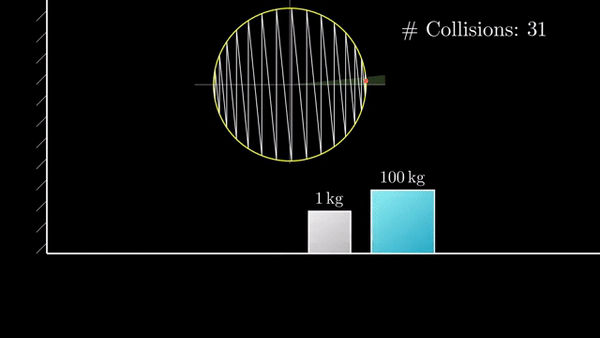
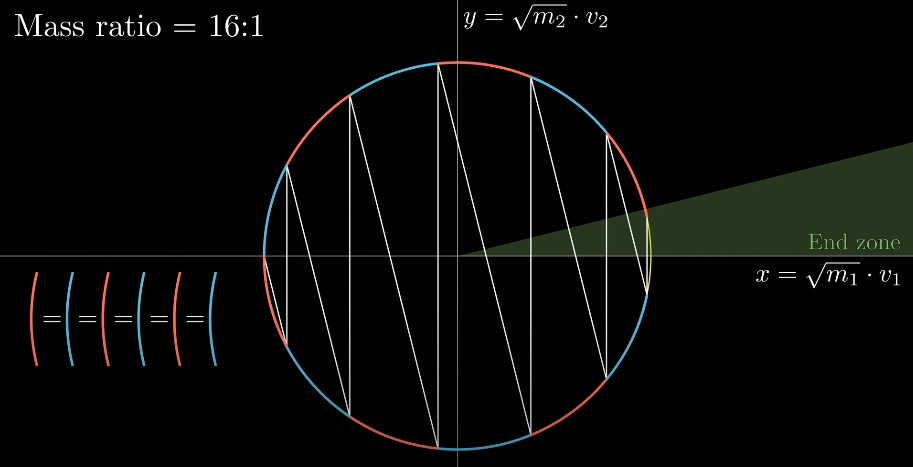
Если присмотреться, можно заметить, что «столкновения» делят окружность на равные дуги. По теореме о вписанном угле. Встает вопрос, сколько дуг получится на окружности?
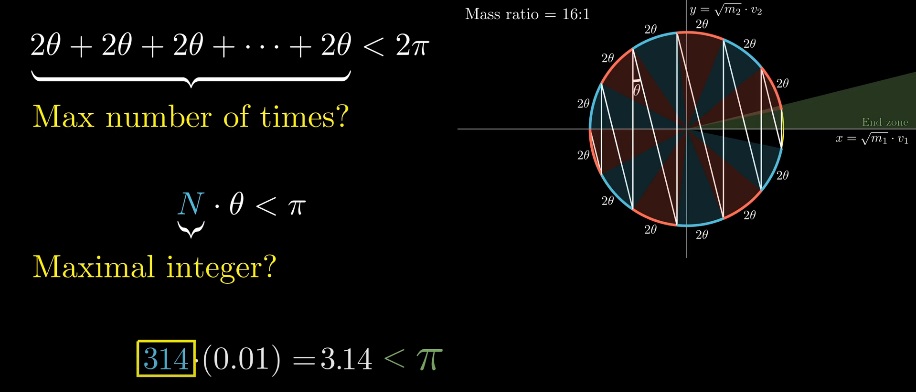
Всего длина окружности 2ℼ, а длина дуги определяется половиной угла, который равен соотношению корней из масс блоков (чем больше разница — тем меньше угол). Порядок разницы масс будет определять «точность» ℼ: 3, 31, 314

Дано: Два блока массой 1 кг и 100 (10 000, 1 000 000,… 100x) кг. Трение в системе отсутствует, удары абсолютно упругие (потерь энергии нет). Более массивный блок ударяет менее массивный и тот отскакивает от него а потом от стенки.
Вопрос: Сколько столкновений совершит маленький блок, пока система не придет в состояние, когда столкновения невозможны?
Ответ невероятен:

В очередной раз поражаюсь изящности объяснений от 3Blue1Brown.
В случае когда массы раны, мы насчитаем 3 столкновения:

Если разница масс в 100 раз, то количество столкновений 31:
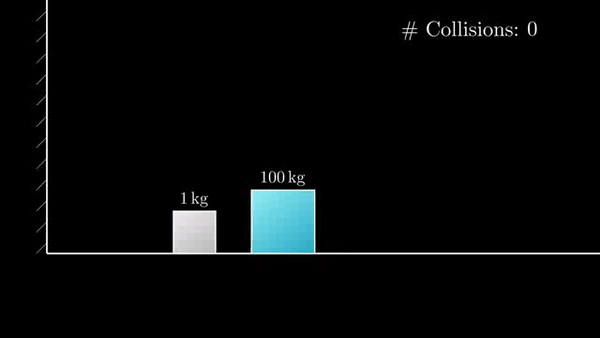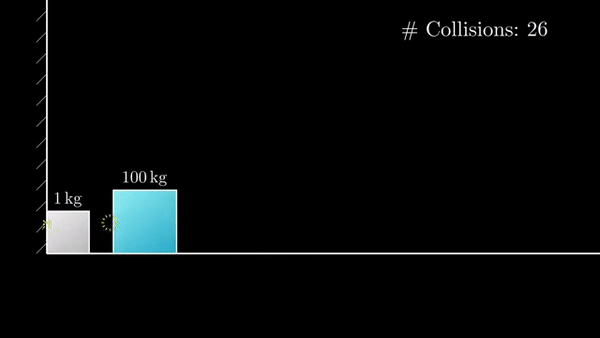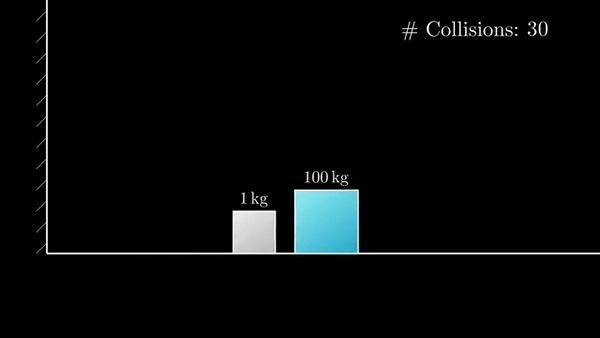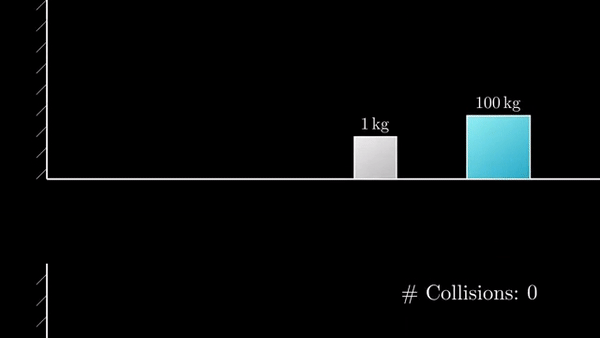
Если разница масс в 10 000 раз, то столкновений будет 314:
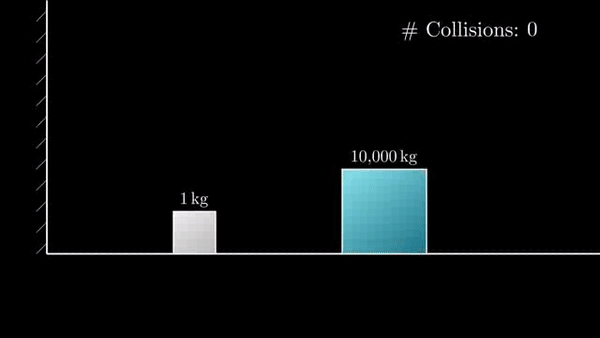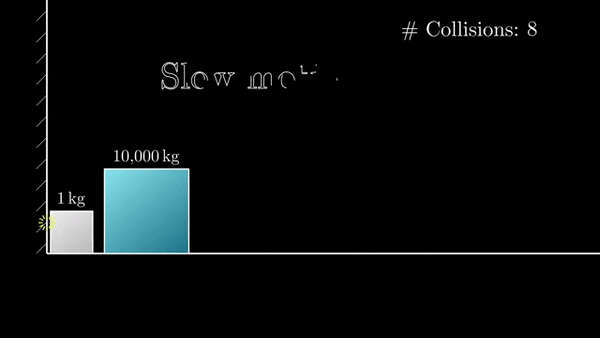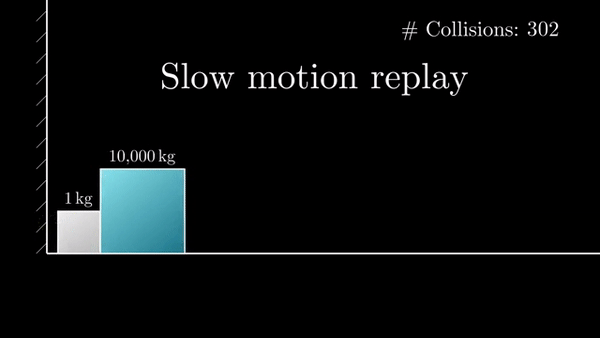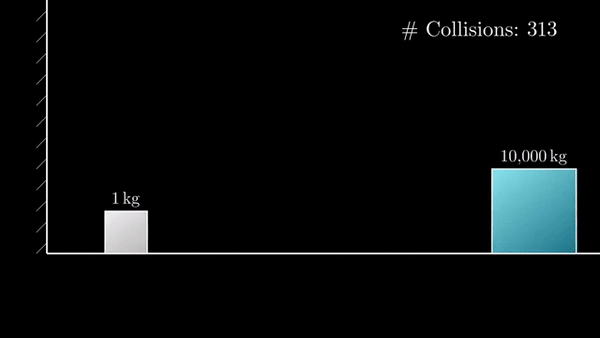
+ еще один удар об стенку
Если разница в 1 000 000 раз, то столкновений 3141:

Если разница в 100 000 000 раз, то столкновений 31415:
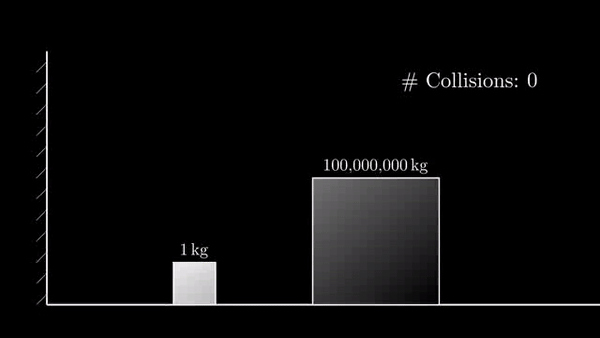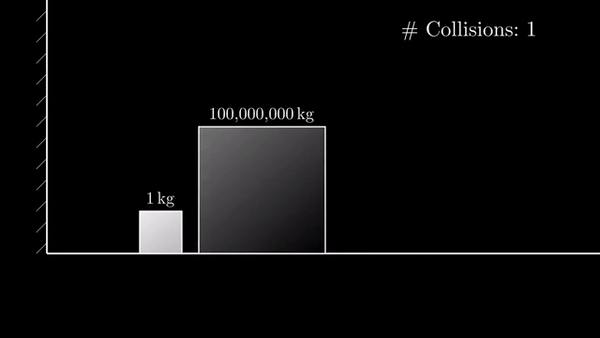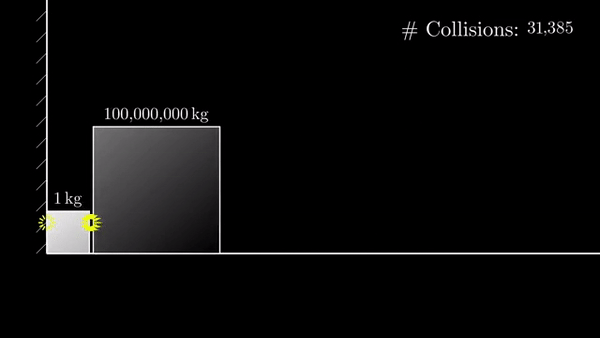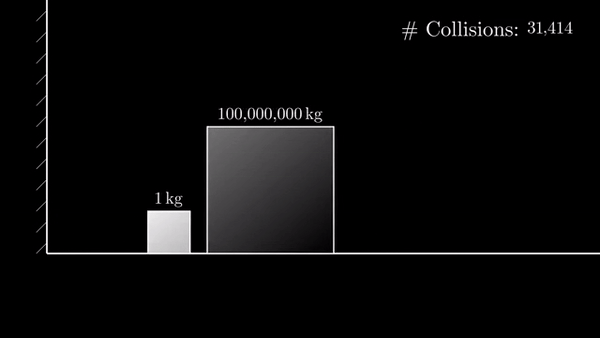
Если разница в 10 000 000 000 раз, то столкновений 314159:

Эта закономерность была открыта Грегори Гальперином в 1995 и опубликована в 2003 году:

PLAYING POOL WITH ℼ (2003)
Данный метод позволяет построить «физическую» машину вычисления числа ℼ с точностью до n-ного знака. Разница масс должна составлять 100(n-1) раз.
С реализацией, конечно, есть нюансы, ну да ладно. Зато красивая идея.
Throwing ℼ at a wall (2006)
Фазовое/конфигурационное пространство

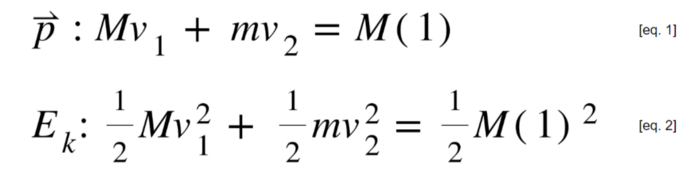
Механическая система описывается двумя законами сохранения: энергии и импульса.
Фазовое пространство для энергии системы представляет собой эллипс, но его можно откалибровать корнем из разницы масс:

Радиус окружности показывает энергию в системе — она всегда постоянная.
При столкновении двух блоков происходит перераспределение импульса и энергии:


Закон сохранения моментов задает угол наклона:

При ударе об стену (объект бесконечной массы) скорость блока меняется на противоположную:

Следующее соударение блоков:

Последующие столкновения:

Фазовая диаграмма удобна тем, что наглядно кодирует состояние системы:


Если присмотреться, можно заметить, что «столкновения» делят окружность на равные дуги. По теореме о вписанном угле. Встает вопрос, сколько дуг получится на окружности?
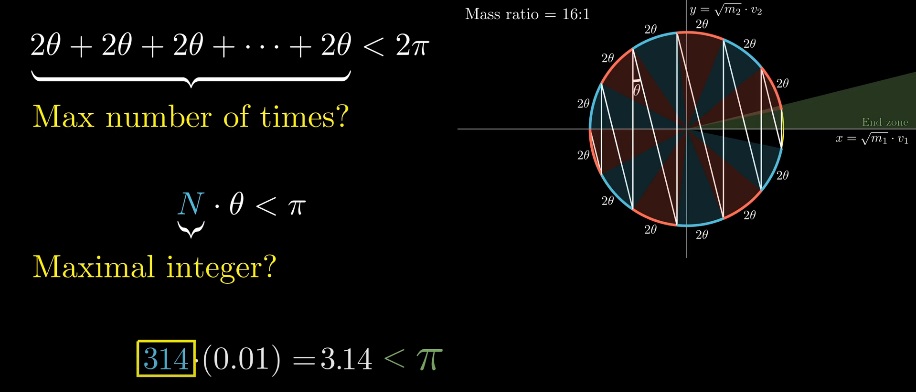
Всего длина окружности 2ℼ, а длина дуги определяется половиной угла, который равен соотношению корней из масс блоков (чем больше разница — тем меньше угол). Порядок разницы масс будет определять «точность» ℼ: 3, 31, 314
Источники
- The Pi Machine: The most unexpected answer to a counting puzzle
- PLAYING POOL WITH ℼ (2003)
- Throwing ℼ at a wall (2006)






