Представьте, что вам нужно сгенерировать равномерно распределённое случайное число от 1 до 10. То есть целое число от 1 до 10 включительно, с равной вероятностью (10%) появления каждого. Но, скажем, без доступа к монетам, компьютерам, радиоактивному материалу или другим подобным источникам (псевдо) случайных чисел. У вас есть только комната с людьми.
Предположим, что в этой комнате чуть более 8500 студентов.
Самое простое — попросить кого-нибудь: «Эй, выбери случайное число от одного до десяти!». Человек отвечает: «Семь!». Отлично! Теперь у вас есть число. Однако вы начинаете задаваться вопросом, является ли оно равномерно распределённым?
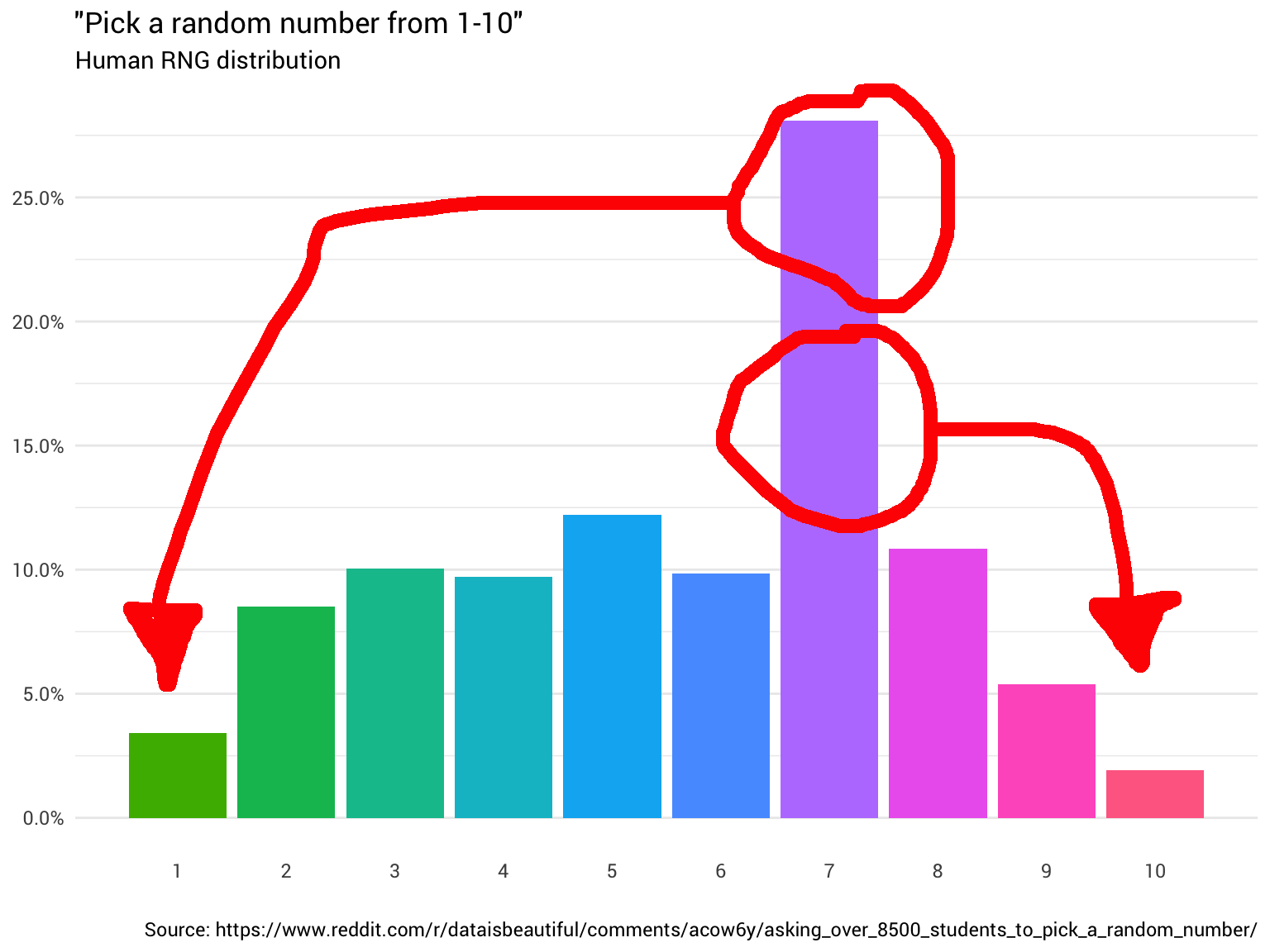
Поэтому вы решили спросить ещё несколько человек. Вы продолжаете их спрашивать и считать их ответы, округляя дробные числа и игнорируя тех, кто думает, что диапазон от 1 до 10 включает 0. В конце концов вы начинаете видеть, что распределение вообще не равномерное:

Данные с Reddit
Вы хлопаете себя по лбу. Ну конечно, оно не будет случайным. В конце концов, нельзя доверять людям.
Вот бы найти какую-то функцию, которая преобразует распределение «человеческого ГСЧ» в равномерное распределение…
Интуиция тут относительно проста. Нужно всего лишь взять массу распределения оттуда, где она выше 10%, и переместить туда, где она меньше 10%. Так, чтобы все столбцы на графике были одного уровня:
По идее, такая функция должна существовать. Фактически, должно быть много различных функций (для перестановки). В крайнем случае, можно «разрезать» каждый столбец на бесконечно малые блоки и построить распределение любой формы (как кирпичики Lego).
Конечно, такой экстремальный пример немного громоздок. В идеале мы хотим сохранить как можно больше исходного распределения (т. е. сделать как можно меньше измельчений и перемещений).
Ну, наше объяснение выше звучит очень похоже на линейное программирование. Из Википедии:
Линейное программирование (LP, также именуется линейной оптимизацией) — метод достижения наилучшего результата… в математической модели, требования которой представлены линейными отношениями… Стандартная форма представляет собой обычную и наиболее интуитивную форму описания задачи линейного программирования. Она состоит из трёх частей:
Аналогично можно сформулировать и проблему перераспределения.
У нас есть набор переменных , каждая из которых кодирует долю вероятности, перераспределённую от целого числа (от 1 до 10) к целому числу (от 1 до 10). Поэтому, если , то нам нужно перенести 20% ответов от семёрки к единице.
Мы хотим ограничить эти переменные таким образом, чтобы все перераспределённые вероятности суммировались в 10%. Другими словами, для каждого от 1 до 10:
Можем представить эти ограничения в виде списка массивов в R. Позже свяжем их в матрицу.
Мы также должны убедиться, что сохраняется вся масса вероятностей из исходного распределения. Так что для каждого в диапазоне от 1 до 10:
Как уже говорилось, мы хотим максимизировать сохранение исходного распределения. Это наша цель (objective):
Затем передаём проблему солверу, например, пакету
Возвращается следующее перераспределение:
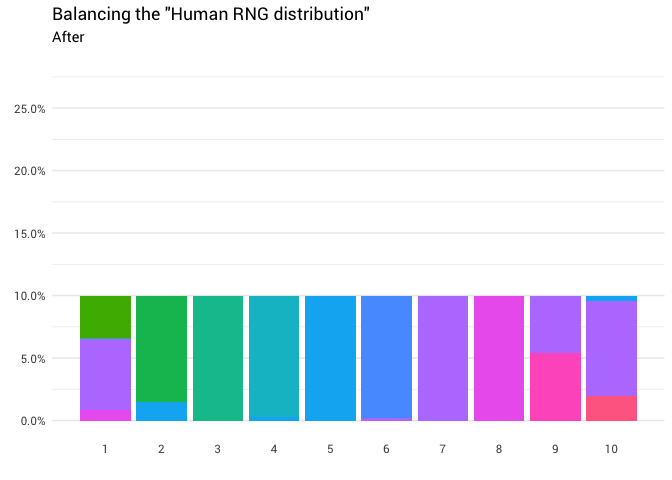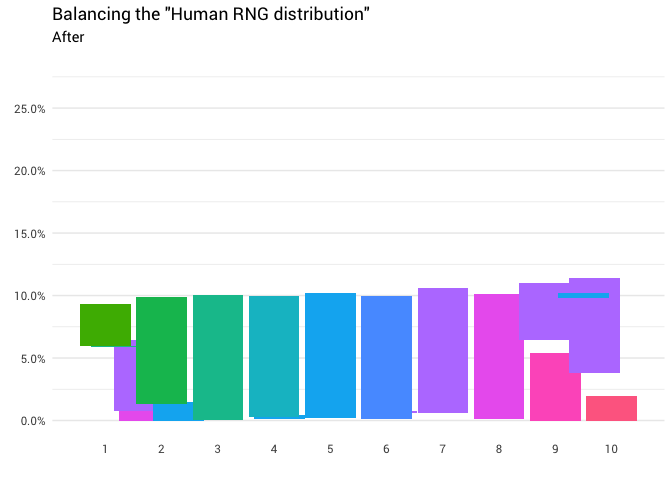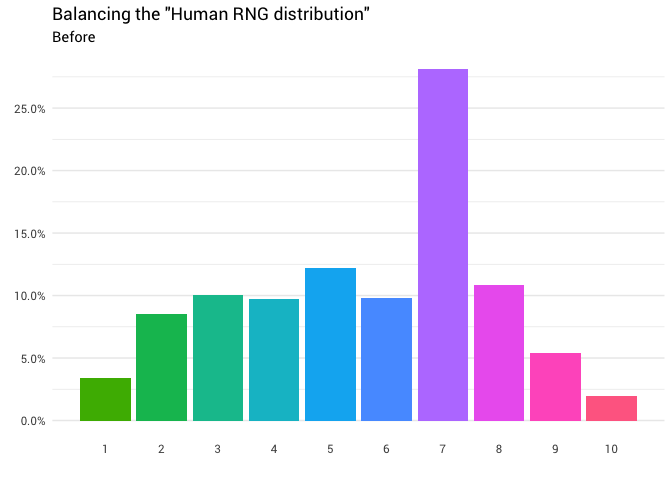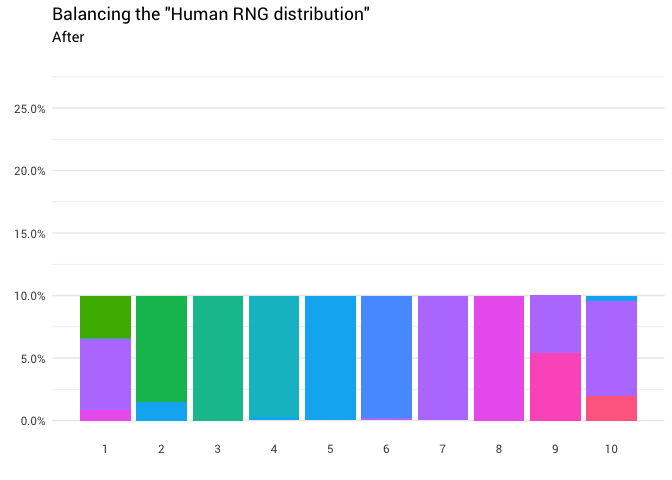
Отлично! Теперь у нас есть функция перераспределения. Давайте поближе посмотрим, как именно движется масса:

Эта диаграмма говорит, что примерно в 8% случаев, когда кто-то называет восемь в качестве случайного числа, вам нужно воспринимать ответ как единицу. В остальных 92% случаев он остаётся восьмёркой.
Было бы довольно просто решить задачу, если бы у нас был доступ к генератору равномерно распределённых случайных чисел (от 0 до 1). Но у нас только комната, полная людей. К счастью, если вы готовы примириться с несколькими небольшими неточностями, то из людей можно сделать довольно хороший ГСЧ, не спрашивая более двух раз.
Возвращаясь к нашему исходному распределению, у нас есть следующие вероятности для каждого числа, которые можно использовать для повторного назначения любой вероятности, если необходимо.
Например, когда кто-то даёт нам восемь в качестве случайного числа, нужно определить, должна ли эта восьмёрка стать единицей или нет (вероятность 8%). Если мы спросим другого человека о случайном числе, то с вероятностью 8,5% он ответит «два». Так что если это второе число равно 2, мы знаем, что должны вернуть 1 как равномерно распределённое случайное число.
Распространив эту логику на все числа, получаем следующий алгоритм:
Предположим, что в этой комнате чуть более 8500 студентов.
Самое простое — попросить кого-нибудь: «Эй, выбери случайное число от одного до десяти!». Человек отвечает: «Семь!». Отлично! Теперь у вас есть число. Однако вы начинаете задаваться вопросом, является ли оно равномерно распределённым?
Поэтому вы решили спросить ещё несколько человек. Вы продолжаете их спрашивать и считать их ответы, округляя дробные числа и игнорируя тех, кто думает, что диапазон от 1 до 10 включает 0. В конце концов вы начинаете видеть, что распределение вообще не равномерное:
library(tidyverse)
probabilities <-
read_csv("https://git.io/fjoZ2") %>%
count(outcome = round(pick_a_random_number_from_1_10)) %>%
filter(!is.na(outcome),
outcome != 0) %>%
mutate(p = n / sum(n))
probabilities %>%
ggplot(aes(x = outcome, y = p)) +
geom_col(aes(fill = as.factor(outcome))) +
scale_x_continuous(breaks = 1:10) +
scale_y_continuous(labels = scales::percent_format(),
breaks = seq(0, 1, 0.05)) +
scale_fill_discrete(h = c(120, 360)) +
theme_minimal(base_family = "Roboto") +
theme(legend.position = "none",
panel.grid.major.x = element_blank(),
panel.grid.minor.x = element_blank()) +
labs(title = '"Pick a random number from 1-10"',
subtitle = "Human RNG distribution",
x = "",
y = NULL,
caption = "Source: https://www.reddit.com/r/dataisbeautiful/comments/acow6y/asking_over_8500_students_to_pick_a_random_number/")
Данные с Reddit
Вы хлопаете себя по лбу. Ну конечно, оно не будет случайным. В конце концов, нельзя доверять людям.
Итак, что делать?
Вот бы найти какую-то функцию, которая преобразует распределение «человеческого ГСЧ» в равномерное распределение…
Интуиция тут относительно проста. Нужно всего лишь взять массу распределения оттуда, где она выше 10%, и переместить туда, где она меньше 10%. Так, чтобы все столбцы на графике были одного уровня:

По идее, такая функция должна существовать. Фактически, должно быть много различных функций (для перестановки). В крайнем случае, можно «разрезать» каждый столбец на бесконечно малые блоки и построить распределение любой формы (как кирпичики Lego).
Конечно, такой экстремальный пример немного громоздок. В идеале мы хотим сохранить как можно больше исходного распределения (т. е. сделать как можно меньше измельчений и перемещений).
Как найти такую функцию?
Ну, наше объяснение выше звучит очень похоже на линейное программирование. Из Википедии:
Линейное программирование (LP, также именуется линейной оптимизацией) — метод достижения наилучшего результата… в математической модели, требования которой представлены линейными отношениями… Стандартная форма представляет собой обычную и наиболее интуитивную форму описания задачи линейного программирования. Она состоит из трёх частей:
- Линейная функция, которую необходимо максимизировать
- Проблемные ограничения следующей формы
- Неотрицательные переменные
Аналогично можно сформулировать и проблему перераспределения.
Представление проблемы
У нас есть набор переменных , каждая из которых кодирует долю вероятности, перераспределённую от целого числа (от 1 до 10) к целому числу (от 1 до 10). Поэтому, если , то нам нужно перенести 20% ответов от семёрки к единице.
variables <-
crossing(from = probabilities$outcome,
to = probabilities$outcome) %>%
mutate(name = glue::glue("x({from},{to})"),
ix = row_number())
variables## # A tibble: 100 x 4 ## from to name ix ## <dbl> <dbl> <glue> <int> ## 1 1 1 x(1,1) 1 ## 2 1 2 x(1,2) 2 ## 3 1 3 x(1,3) 3 ## 4 1 4 x(1,4) 4 ## 5 1 5 x(1,5) 5 ## 6 1 6 x(1,6) 6 ## 7 1 7 x(1,7) 7 ## 8 1 8 x(1,8) 8 ## 9 1 9 x(1,9) 9 ## 10 1 10 x(1,10) 10 ## # … with 90 more rows
Мы хотим ограничить эти переменные таким образом, чтобы все перераспределённые вероятности суммировались в 10%. Другими словами, для каждого от 1 до 10:
Можем представить эти ограничения в виде списка массивов в R. Позже свяжем их в матрицу.
fill_array <- function(indices,
weights,
dimensions = c(1, max(variables$ix))) {
init <- array(0, dim = dimensions)
if (length(weights) == 1) {
weights <- rep_len(1, length(indices))
}
reduce2(indices, weights, function(a, i, v) {
a[1, i] <- v
a
}, .init = init)
}
constrain_uniform_output <-
probabilities %>%
pmap(function(outcome, p, ...) {
x <-
variables %>%
filter(to == outcome) %>%
left_join(probabilities, by = c("from" = "outcome"))
fill_array(x$ix, x$p)
})Мы также должны убедиться, что сохраняется вся масса вероятностей из исходного распределения. Так что для каждого в диапазоне от 1 до 10:
one_hot <- partial(fill_array, weights = 1)
constrain_original_conserved <-
probabilities %>%
pmap(function(outcome, p, ...) {
variables %>%
filter(from == outcome) %>%
pull(ix) %>%
one_hot()
})Как уже говорилось, мы хотим максимизировать сохранение исходного распределения. Это наша цель (objective):
maximise_original_distribution_reuse <-
probabilities %>%
pmap(function(outcome, p, ...) {
variables %>%
filter(from == outcome,
to == outcome) %>%
pull(ix) %>%
one_hot()
})
objective <- do.call(rbind, maximise_original_distribution_reuse) %>% colSums()Затем передаём проблему солверу, например, пакету
lpSolve в R, объединив созданные ограничения в одну матрицу:# Make results reproducible...
set.seed(23756434)
solved <- lpSolve::lp(
direction = "max",
objective.in = objective,
const.mat = do.call(rbind, c(constrain_original_conserved, constrain_uniform_output)),
const.dir = c(rep_len("==", length(constrain_original_conserved)),
rep_len("==", length(constrain_uniform_output))),
const.rhs = c(rep_len(1, length(constrain_original_conserved)),
rep_len(1 / nrow(probabilities), length(constrain_uniform_output)))
)
balanced_probabilities <-
variables %>%
mutate(p = solved$solution) %>%
left_join(probabilities,
by = c("from" = "outcome"),
suffix = c("_redistributed", "_original"))Возвращается следующее перераспределение:
library(gganimate)
redistribute_anim <-
bind_rows(balanced_probabilities %>%
mutate(key = from,
state = "Before"),
balanced_probabilities %>%
mutate(key = to,
state = "After")) %>%
ggplot(aes(x = key, y = p_redistributed * p_original)) +
geom_col(aes(fill = as.factor(from)),
position = position_stack()) +
scale_x_continuous(breaks = 1:10) +
scale_y_continuous(labels = scales::percent_format(),
breaks = seq(0, 1, 0.05)) +
scale_fill_discrete(h = c(120, 360)) +
theme_minimal(base_family = "Roboto") +
theme(legend.position = "none",
panel.grid.major.x = element_blank(),
panel.grid.minor.x = element_blank()) +
labs(title = 'Balancing the "Human RNG distribution"',
subtitle = "{closest_state}",
x = "",
y = NULL) +
transition_states(
state,
transition_length = 4,
state_length = 3
) +
ease_aes('cubic-in-out')
animate(
redistribute_anim,
start_pause = 8,
end_pause = 8
)
Отлично! Теперь у нас есть функция перераспределения. Давайте поближе посмотрим, как именно движется масса:
balanced_probabilities %>%
ggplot(aes(x = from, y = to)) +
geom_tile(aes(alpha = p_redistributed, fill = as.factor(from))) +
geom_text(aes(label = ifelse(p_redistributed == 0, "", scales::percent(p_redistributed, 2)))) +
scale_alpha_continuous(limits = c(0, 1), range = c(0, 1)) +
scale_fill_discrete(h = c(120, 360)) +
scale_x_continuous(breaks = 1:10) +
scale_y_continuous(breaks = 1:10) +
theme_minimal(base_family = "Roboto") +
theme(panel.grid.minor = element_blank(),
panel.grid.major = element_line(linetype = "dotted"),
legend.position = "none") +
labs(title = "Probability mass redistribution",
x = "Original number",
y = "Redistributed number")
Эта диаграмма говорит, что примерно в 8% случаев, когда кто-то называет восемь в качестве случайного числа, вам нужно воспринимать ответ как единицу. В остальных 92% случаев он остаётся восьмёркой.
Было бы довольно просто решить задачу, если бы у нас был доступ к генератору равномерно распределённых случайных чисел (от 0 до 1). Но у нас только комната, полная людей. К счастью, если вы готовы примириться с несколькими небольшими неточностями, то из людей можно сделать довольно хороший ГСЧ, не спрашивая более двух раз.
Возвращаясь к нашему исходному распределению, у нас есть следующие вероятности для каждого числа, которые можно использовать для повторного назначения любой вероятности, если необходимо.
probabilities %>%
transmute(number = outcome,
probability = scales::percent(p))## # A tibble: 10 x 2 ## number probability ## <dbl> <chr> ## 1 1 3.4% ## 2 2 8.5% ## 3 3 10.0% ## 4 4 9.7% ## 5 5 12.2% ## 6 6 9.8% ## 7 7 28.1% ## 8 8 10.9% ## 9 9 5.4% ## 10 10 1.9%
Например, когда кто-то даёт нам восемь в качестве случайного числа, нужно определить, должна ли эта восьмёрка стать единицей или нет (вероятность 8%). Если мы спросим другого человека о случайном числе, то с вероятностью 8,5% он ответит «два». Так что если это второе число равно 2, мы знаем, что должны вернуть 1 как равномерно распределённое случайное число.
Распространив эту логику на все числа, получаем следующий алгоритм:
По этому алгоритму вы можете использовать группу людей для получения чего-то близкого к генератору равномерно распределённых случайных чисел от 1 до 10!
- Спросить у человека случайное число, .
- или :
- Ваше случайное число
- Если :
- Спросить у другого человека случайное число ()
- Если (12.2%):
- Ваше случайное число 2
- Если (1.9%):
- Ваше случайное число 4
- В противном случае, ваше случайное число 5
- Если :
- Спросить у другого человека случайное число ()
- Если или (20.7%):
- Ваше случайное число 1
- Если или (16.2%):
- Ваше случайное число 9
- Если (28.1%):
- Ваше случайное число 10
- В противном случае, ваше случайное число 7
- Если :
- Спросить у другого человека случайное число ()
- Если (8.5%):
- Ваше случайное число 1
- В противном случае, ваше случайное число 8





