Какой следующий член…? — Ищем формулу для n-го члена последовательности, производящие функции и Z-преобразование

Скачать файл с кодом и данные можно в оригинале поста в моем блоге

В языке Wolfram Language есть четыре совершенно потрясающие функции: FindSequenceFunction, RSolve, DifferenceRootReduce и FindFormula. В этой статье мы обсудим их возможности и поговорим о функциях, тесно с ними связанных — для поиска параметров линейной рекурсии FindLinearRecurrence (коэффициентов линейного рекуррентного уравнения), производящих функциях GeneratingFunction и Z-преобразовании ZTransform.

Первая функция — FindSequenceFunction — по последовательности чисел ищет выражение для её n-го члена не требуя вообще ничего более.

Hold @ FindSequenceFunction[{1, 1, 2, 3, 5, 8, 13}, n]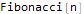

FindSequenceFunction[
{-2, 4Sqrt[Pi],
-16, 16Sqrt[Pi],
-128/3, 32Sqrt[Pi],
-1024/15, 128Sqrt[Pi]/3,
-8192/105, 128Sqrt[Pi]/3},
n]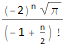

Вторая функция — RSolve — решает рекуррентные уравнения самых разных типов. Элементы могут иметь вид $$, $$, $$, где f имеет вид: n+A (арифметические разностные уравнения), B*n — геометрические или q-разностные уравнения), B*n+a (арифметико-геометрические функциональные разностные уравнения), B*n^d (степеные геометрические функциональные разностные уравнения), (A*n+B)/(C*n+D) (линейные дробные функциональные разностные уравнения).

RSolve[
	{
		a[n + 3]==2 * a[n],
		a[1]==α,
		a[2]==β,
		a[3]==γ
	},
	a, n
]

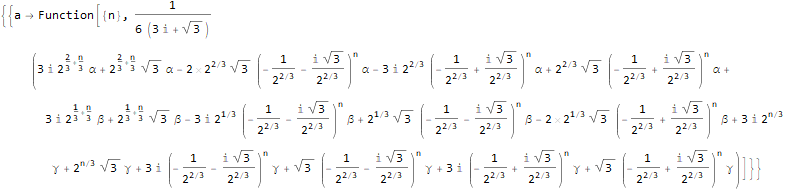
RSolve[
	{
		v[n]==(2 * Pi * v[n - 2]) / n,
		v[2]==Pi,
		v[3]==(4 * Pi) / 3
	},
	v @ n, n
]

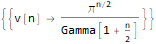
Третья функция — DifferenceRootReduce — ищет рекуррентное соотношение для последовательности чисел, n-й член которой имеет заданный вид.

DifferenceRootReduce[-2 * n * Pi * Factorial[(n * 2) - 1],
	n
]

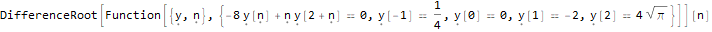
RSolve[
	{
		(-8 * y[n]) + n * y[2 + n]==0,
		y[-1]==1/4,
		y[0]==0,
		y[1]==-2,
		y[2]==4Sqrt[Pi]
	},
	y, n
]

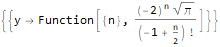
Эта функция может много чего ещё, скажем, проверять тождества относительно последовательностей, к примеру:

DifferenceRootReduce[Fibonacci[2 * n]==Fibonacci[n] * LucasL[n], n]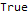

Здесь LucasL — последовательность чисел Люка (это, по сути, последовательность Фибоначчи, только первые члены не 1, 1, а 1, 3.

Hold @ DifferenceRootReduce @ LucasL @ n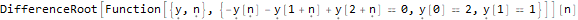

DifferenceRootReduce[LucasL[n]==Fibonacci[n - 1] + Fibonacci[n + 1]]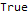

Как найти рекуррентную формулу для последовательности?

Метод поиска общего члена последовательности часто основан на том, что нужно подобрать рекуррентное уравнение.

Работать это может примерно так: пусть мы ищем n-й член последовательности в виде $$. Пусть у нас есть первые члены последовательности:

sequence = {1, 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860, 33461}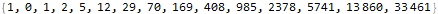

Попробуем найти выражение для n-го члена в виде $$:

seauenseEq1 = MovingMap[
	Function[
		Dot[Part[#, 1;;1], {a @ 1}]==Part[#, -1]
	],
	sequence, 1
]

Hold @ Solve @ seauenseEq1

Как видно, решений нет.

Попробуем искать теперь в виде $$:

seauenseEq2 = MovingMap[
	Function[
		Dot[Part[#, 1;;2], {a @ 1, a @ 2}]==Part[#, -1]
	],
	sequence, 2
]

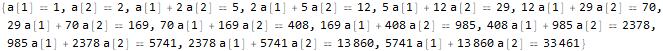
Hold @ Solve @ seauenseEq2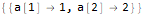

Как видим, получилось. Значит, n-й член имеет вид: $$.

На самом деле есть встроенная функция FindLinearRecurrence, которая позволяет найти линейную рекурсию, подобно тому, как мы это только что сделали:

Hold @ FindLinearRecurrence @ sequence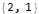

Используя функцию LinearRecurrence можно продлить последовательность:

LinearRecurrence[{2, 1}, sequence[[1;;2]], 50]

Или объединить все в одну строчку, построив функцию, которая: продлит последовательность, выдаст разностное уравнение и найдет общую формулу для n-го члена:

sequenseExtension[list_, n_] := Module[
	{lr, eq},
	lr = FindLinearRecurrence @ list;
	eq = Flatten[
		{
			a[k]==Total[
					Table[
						a[k + -i] * Part[lr, i],
						{i, 1, Length @ lr}
					]
				],
			Table[a[i], list[[i]]], {i, 1, Length @ lr}]
		}
	];
	<|
		"Уравнение" -> eq,
		"Формула" -> FullSimplify[a[k] /. Part[RSolve[eq, a, k], 1]],
		"Продление" -> LinearRecurrence[lr, Part[list, Span[1, Length[lr]]], n]
	|>
];

Hold @ sequenseExtension[{1, 1, 2, 3, 5}, 20]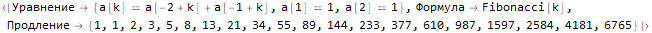

Hold @ sequenseExtension[{1, 2, 2, 1, 1, 2, 2, 1}, 20]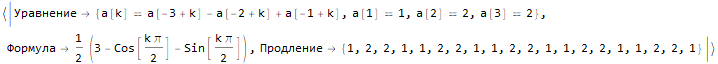

Hold @ sequenseExtension[
{1, 0, -1, 0, 2, 0, -2, 0, 3, 0, -3, 0, 4, 0, -4},
25
]

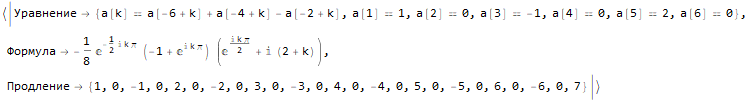
Как найти формулу для n-го члена последовательности?

Z-преобразование

Z-преобразование состоит в вычислении ряда вида $$ от дискретной функции $$. Это преобразование позволяет свести рекуррентное уравнение для задания последовательности к уравнению относительно образа функции $$, что аналогично преобразованию Лапласа, которое сводит дифференциальные уравнения к алгебраическим.

Вот как это работает:

Grid[
	Transpose[
		Function[
			{
				#,
				Map[TraditionalForm, Map[FullSimplify, ZTransform[#, n, z]]]
			}
		][
			{
				f[n - 2],
				f[n - 1],
				f @ n,
				f[n + 1],
				f[n + 2]
			}
		]
	],
	Background -> White, Dividers -> All
]

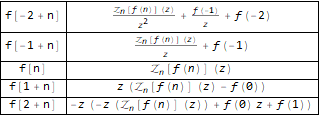
Посмотрим на примере, скажем, возьмем хорошо известную последовательность Фибоначчи:

fibonacciEq = f[n]==f[n - 1] + f[n - 2];

initialConditions = {f[1] -> 1, f[2] -> 1};

Ясно, что её стоит переписать в виде, как показано ниже, чтобы не появлялись конструкции типа $$ после применения Z-преобразования.

fibonacciEq = f[n + 2]==f[n + 1] + f[n];

initialConditions = {f[0] -> 1, f[1] -> 1};

Осуществим Z-преобразование:

fibonacciEqZTransformed = ReplaceAll[fibonacciEq, pattern:f[__] :> ZTransform[pattern, n, z]]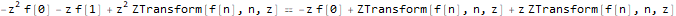

Решим уравнение относительно образа функции f — ZTransform[f[n],n,z]:

fZTransformed = ReplaceAll[
	ZTransform[f @ n, n, z],
	Part[Solve[fibonacciEqZTransformed, ZTransform[f @ n, n, z]], 1]
]

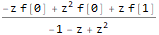
Выполним обратное Z-преобразование, подставив одновременно начальные условия (заменим n на n-1 в финальном выражении, чтобы наша последовательность имела правильную индексацию (с первого, а не нулевого члена):

ReplaceAll[InverseZTransform[fZTransformed /. initialConditions, z, n],
	n -> (n - 1)
]

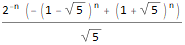
Естестевенно это можно автоматизировать, создав свой аналог RSolve:

myRSolve[eq_, initials_, f_, n_] := Module[
	{z, initialsInner, eqZTransformed, fZTransformed},
	initialsInner = ReplaceAll[initials, f[x_] :> f[x - 1]];
	eqZTransformed = ReplaceAll[eq, pattern:f[__] :> ZTransform[pattern, n, z]];
	fZTransformed = ReplaceAll[ZTransform[f @ n, n, z],
		Part[Solve[eqZTransformed, ZTransform[f @ n, n, z]], 1]
	];
	FullSimplify[
		InverseZTransform[fZTransformed /. initialsInner, z, n] /. n -> (n - 1)
	]
];

myRSolve[
	{
		f[n + 2]==(2 * f[n + 1]) + -(5 * f[n])
	},
	{f[1] -> 20, f[2] -> 0},
	f, n
]

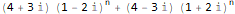
RSolve[
	{
		f[n + 2]==(2 * f[n + 1]) + -(5 * f[n]),
		f[1]==20,
		f[2]==0
	},
	f, n
]

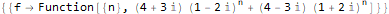
Но, конечно, RSolve содержит намного больше возможностей для решения самых разных дискретных уравнений, на которых мы не будем останавливаться подробнее:

RSolve[a[n]==(n * a[n]) + n, a, n],
RSolve[
	{
		a[n + 1]==(2 * a[n]) + (3 * a[n]) + 4,
		a[0]==0
	},
	a, n
],
RSolve[
	y[n + 1 * 3]==(2 * y[n + 1 * 6]) + n * 2,
	y, n
]

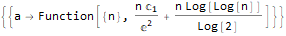
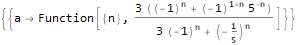
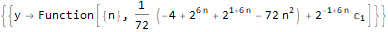
Производящие функции

Производящая функция последовательности $$ это такая функция $$, разложение которой в ряд Тейлора (или, более широко, Лорана) имеет вид — $$. Другими словами, коэффициенты при степенях x в разложении функции в ряд задают нашу последовательность.

Скажем, функция $$ является производящей функцией последовательности 1, 1, 1, 1, ...:

Series[1 / (1 + -x), {x, 0, 10}]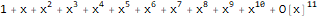

А функция $$ является производящей функцией последовательности Фибоначчи 1, 1, 2, 3, 5, 8, 13, ...:

Series[(1 * 1) + (-x) + -(x * 2),
	{x, 0, 10}
]

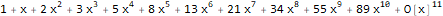
Ещё есть разновидность производящей функции — экспоненциальная производящая функция, которая для последовательности $$ имеет вид — $$.

Скажем, для последовательностей 1, 1, 1, 1… и 1, 1, 2, 3, 5, 8, 13,… экспоненциальные производящие функции таковы — $$ и $$:

ReplaceAll[Normal[Series[E ^ x, {x, 0, 10}]],
	Power[x, n_] :> ((x ^ n) * Factorial[n])
]

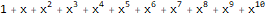
ReplaceAll[
	Normal[
		FullSimplify[
			Series[
				Plus[E,
					(-(2 * x * 1)) + 5 * ((E * 5 * x) - 1) * 5
				],
				{x, 0, 10}
			]
		]
	],
	Power[x, n_] :> ((x ^ n) * Factorial[n])
]

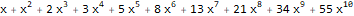
Производящую функцию в Wolfram Language можно найти двумя функциями — GeneratingFunction и FindGeneratingFunction (экспоненциальную с помощью ExponentialGeneratingFunction):

GeneratingFunction[-(m * Factorial[n]), {n, m}, {x, y}]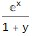

TraditionalForm[
	FullSimplify[
		ExponentialGeneratingFunction[-(n * Factorial[n - 1] * Factorial[2 * n]), n, x]
	]
]

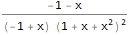
Есть много методов поиска общего члена последовательности с помощью производящих функций. Не будем подробно останавливаться на этом, скажем, только что неплохая теория есть на сайте genfunc.ru.

Один из методов похож на Z-преобразование:

generatingFEq = ReplaceAll[
	f[n + 2]==f[n + 1] + f[n],
	pattern:f[__] :> GeneratingFunction[pattern, n, z]
],
generatingF = ReplaceAll[
	GeneratingFunction[f @ n, n, z],
	Part[Solve[generatingFEq, GeneratingFunction[f @ n, n, z]], 1]
],
nthTerm = SeriesCoefficient[generatingF, {z, 0, n}],
FullSimplify[
	ReplaceAll[ReplaceAll[nthTerm, {f[0] -> 1, f[1] -> 1}],
		n -> (n - 1)
	],
	GreaterEqual[n, 1]
]

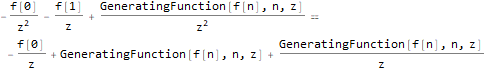
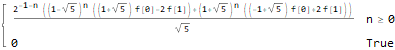
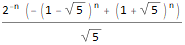
OEIS — Онлайн-энциклопедия целочисленных последовательностей и интеграция с Wolfram Language

В интернете доступна совершенно потрясающая коллекция числовых последовательностей — OEIS (On-Line Encyclopedia of Integer Sequences). Она была создана Нилом Слоуном во время его исследовательской деятельности в AT&T Labs. В OEIS хранится информация о целочисленных последовательностях, представляющих интерес как для любителей, так и для специалистов в математике, комбинаторике, теории чисел, теории игр, физике, химии, биологии, информатике. На данный момент там собрано 329085 последовательностей. Запись в OEIS включает в себя первые элементы последовательности, ключевые слова, математическое описание, фамилии авторов, ссылки на литературу; присутствует возможность построения графика или проигрывания музыкального представления последовательности. Поиск в базе данных может осуществляться по ключевым словам и по подпоследовательности.

Недавно появилась интеграция с этой базой внутри Wolfram Language (при использовании важно понимать, что это разработка пользователей — с недавного времени можно выгружать свой код в репозиторий Wolfram Function Repository). Достаточно просто указать номер интересующей вас последовательности или список номеров.

OEISSequenceData = ResourceFunction @ "OEISSequenceData";

OEISSequence = ResourceFunction @ "OEISSequence";

ResourceFunction[«OEISSequence»] — просто выдает первые члены последовательности:

Hold @ OEISSequence @ "A666"

ResourceFunction[«OEISSequenceData»] — выдает датасет с полной информацией из базы:

sequenceData[666] = OEISSequenceData[666, "Dataset"]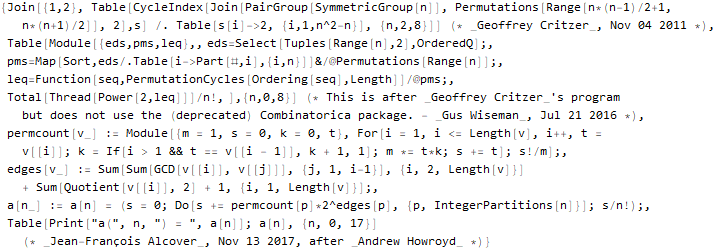

Скажем, можно «вытащить» код на языке Wolfram Language:

Hold @ Normal @ sequenceData[666]["CodeWolframLanguageStrings"]

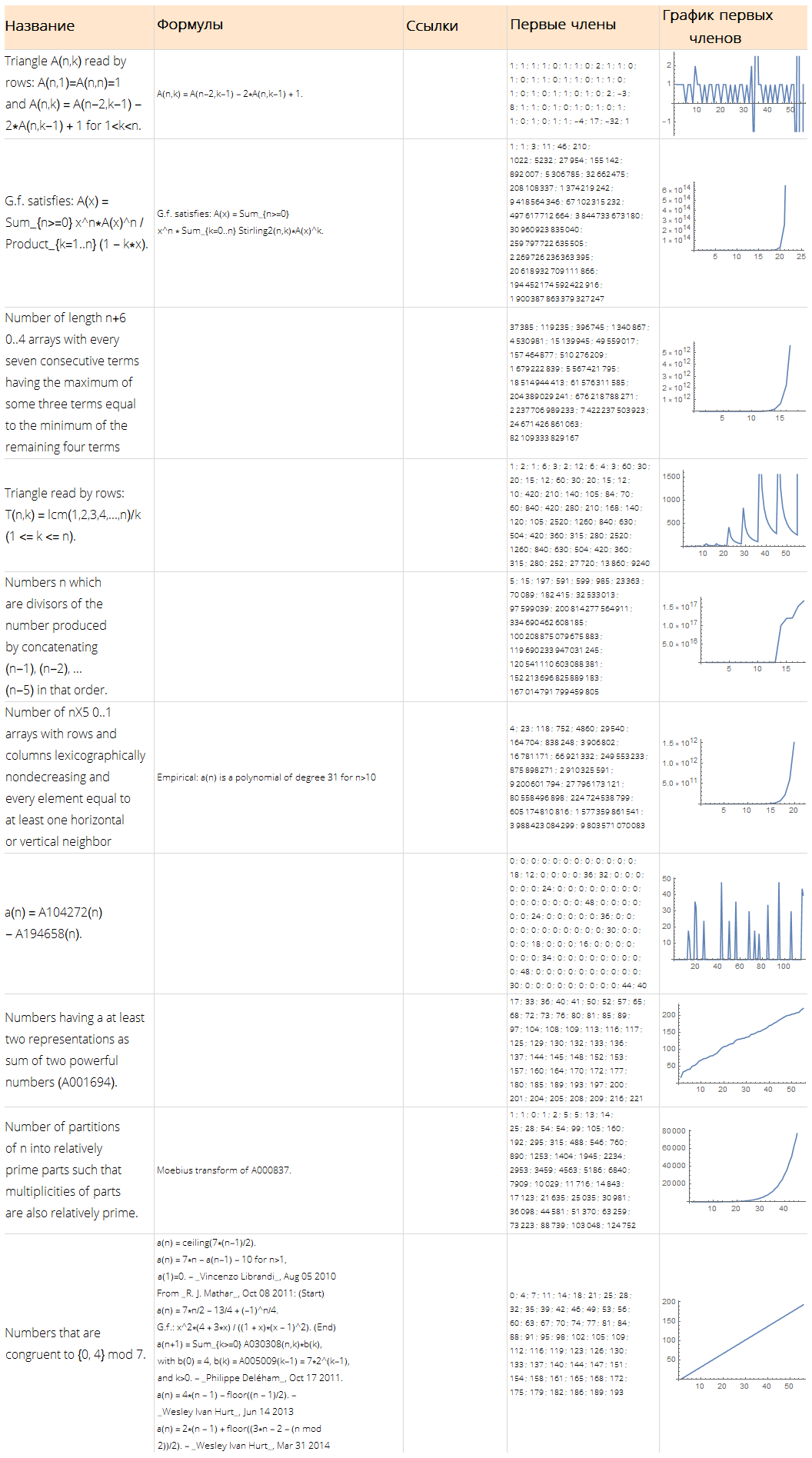
Или набор случайно выбранных последовательностей с интересующей по ним информацией:

randomSequences = Dataset @ Map[
	Normal,
	OEISSequenceData[RandomInteger[{1, 300000}, 10], "Dataset"]
];

Function[
	Framed[#, FrameStyle -> None, FrameMargins -> 5, Background -> White]
][
	Grid[
		Join[
			{
				Map[Style[#, Bold, 18]&,
					{"Название", "Формулы", "Ссылки", "Первые члены", "График первых членов"}
				]
			},
			Map[
				Function[
					Map[
						Function[
							TextCell[#, LineIndent -> 0, FontSize -> 12, FontFamily -> "Open Sans Light"]
						],
						{
							Style[Part[#, 1], 16],
							Row[Part[#, 4], "\n"],
							Row[Part[#, 3], "\n"],
							Style[Row[Part[#, 2], "; "], 10],
							ListLinePlot[Part[#, 2], ImageSize -> Full]
						}
					]
				],
				Values @ Normal @ randomSequences[All, {"Name", "Sequence", "References", "Formulae"}]
			]
		],
		Dividers -> {{None, {LightGray}, None}, {None, {LightGray}, None}},
		ItemStyle -> Directive[FontSize -> 12, FontFamily -> "Open Sans Light"],
		ItemSize -> {{15, 25, 10, 15, 15}, Automatic},
		Alignment -> {Left, Center},
		Background -> {None, {LightOrange, White}}
	]
]

Поиск потенциально возможной формулы

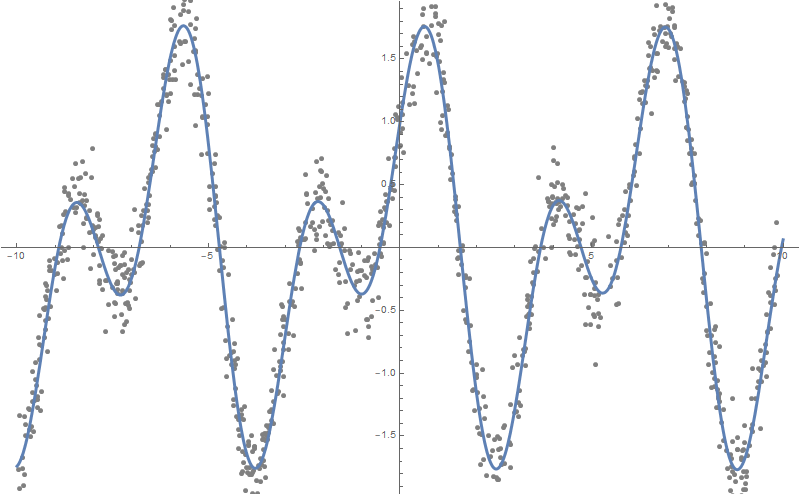
Наконец, хотелось бы отметить функцию FindFormula, которая по заданному набору чисел строит формулу, которая их может описать. Примем зависимостей подобрать можно много и из разных классов функций.

data = Table[
  {
    x,
    Sin[2 * x] + Cos[x] + RandomVariate[NormalDistribution[0, 0.2]]
  },
  {x, RandomReal[{-10, 10}, 1000]}
];

ListPlot[data, Background -> White, ImageSize -> 600]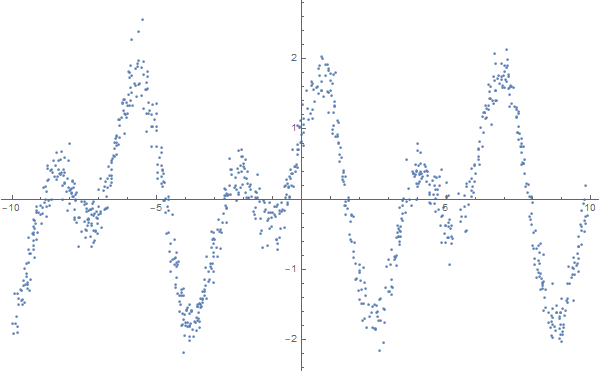

formulas = FindFormula[data, x]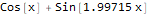

Как видно, Wolfram Language подобрал функцию, очень близкую к той, на основе которой были построены «зашумленные» данные, а именно — Sin[2x]+Cos[x]:

Plot[formulas,
	{x, -10, 10},
	PlotStyle -> AbsoluteThickness[3],
	Prolog -> {AbsolutePointSize[5], Gray, Point @ data},
	Background -> White, ImageSize -> 800, PlotLegends -> "Expressions"
]

Можно построить и большее количество зависимостей, скажем, 10:

formulas = FindFormula[data, x, 10]

Plot[formulas,
	{x, -10, 10},
	PlotStyle -> AbsoluteThickness[3],
	Prolog -> {AbsolutePointSize[5], LightGray, Point @ data},
	Background -> White, ImageSize -> 800, PlotLegends -> "Expressions"
]

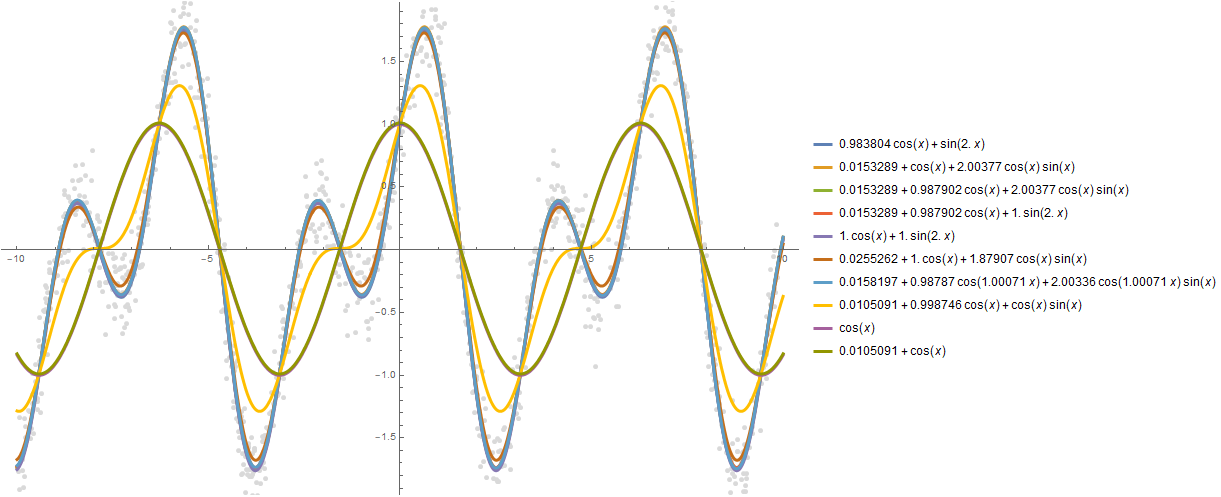
Стоит отметить, что есть функция, аналогичная по функционалу, которая ищет вероятностное распределение — FindDistribution.

Для сотрудничества — пишите личное сообщение на Хабре или в мою группу ВКонтакте.
Канал YouTube — вебинары и обучающие ролики.
Регистрация на новые курсы. Готовый онлайн курс.