Книга «Классические задачи Computer Science на языке Java»

Привет, Хаброжители! Cтолкнулись с «неразрешимой» проблемой при разработке программного обеспечения? Скорее всего, кто-то уже справился с этой задачей, и вы можете не ломать голову. Дэвид Копец собрал наиболее полезные готовые решения, принципы и алгоритмы. «Классические задачи Computer Science на языке Java» — это мастер-класс по программированию, содержащий 55 практических примеров, затрагивающих самые актуальные темы: базовые алгоритмы, ограничения, искусственный интеллект и многое другое.

В этой книге:

— Рекурсия, мемоизация и битовые манипуляции.
— Поисковые, графовые и генетические алгоритмы.
— Проблемы ограничений.
— Кластеризация методом k-среднего, нейронные сети и состязательный поиск.

Состязательный поиск

Идеальная информационная игра для двух игроков с нулевой суммой и точной информацией — это игра, в которой оба соперника имеют всю доступную им информацию о состоянии игры и все, что является преимуществом для одного, становится потерей преимущества для другого. К таким играм относятся крестики-нолики, Connect Four, шашки и шахматы. В этой главе вы узнаете, как создать сильного искусственного соперника, способного играть в такие игры. В сущности, обсуждаемые методы в сочетании с современными вычислительными возможностями позволяют создавать искусственных соперников, которые прекрасно играют в простые игры этого класса и способны играть в сложные игры, выходящие за пределы возможностей любого соперника-человека.

8.1. Основные компоненты настольной игры

Как и при рассмотрении большинства более сложных задач в предыдущих главах, постараемся сделать решение как можно более обобщенным. В случае состязательного поиска это означает, что наши алгоритмы поиска не должны зависеть от игры. Начнем с определения нескольких простых базовых классов, которые выявляют состояние, необходимое алгоритмам поиска. Затем создадим подклассы базовых классов для конкретных игр (крестики-нолики и Connect Four) и введем эти подклассы в алгоритмы поиска, чтобы они могли «играть» в эти игры. Вот базовые классы (листинг 8.1).

Листинг 8.1. Piece.java

package chapter8;

public interface Piece {
     Piece opposite();
}

Совет
Поскольку в крестиках-ноликах и игре Connect Four существует только один вид фигур, класс Piece в этой главе может использоваться как индикатор хода. В более сложных играх, таких как шахматы, где есть разные виды фигур, ходы могут обозначаться целым числом или логическим значением. В качестве альтернативы можно применять для обозначения хода атрибут color более сложного типа Piece.

Piece — это базовый класс для фигуры на доске в игре. Его другая роль — индикатор хода. Именно для этого необходимо свойство opposite. Нам нужно знать, чей ход следует за текущим ходом (листинг 8.2).

Листинг 8.2. Board.java

package chapter8;

import java.util.List;

public interface Board<Move> {

     Piece getTurn();

     Board<Move> move(Move location);

     List<Move> getLegalMoves();

     boolean isWin();

     default boolean isDraw() {
         return !isWin() && getLegalMoves().isEmpty();
     }

     double evaluate(Piece player);
}

Класс Board является фактическим хранилищем состояния. Для любой конкретной игры, которую будут выполнять алгоритмы поиска, они должны уметь ответить на следующие вопросы.

• Чей сейчас ход?

• Какие ходы можно сделать из текущей позиции согласно правилам?

• Выиграна ли сейчас игра?

• Сыграна ли игра вничью?

Последний вопрос, касающийся ничьих, на самом деле комбинация двух предыдущих вопросов для многих игр. Если игра не выиграна, но возможных ходов нет, то это ничья. Вот почему в классе Board сразу можно создать конкретную реализацию метода isDraw(). Кроме того, есть еще несколько действий, которые необходимо реализовать.

• Сделать ход, чтобы перейти из текущей в новую позицию.

• Оценить позицию, чтобы увидеть, какой игрок имеет преимущество.

Каждый метод и свойство класса Board являются реализацией одного из предыдущих вопросов или действий. На языке игры класс Board можно было бы назвать Position, но мы используем это имя для чего-то более конкретного в каждом из подклассов.

Класс Board имеет общий тип Move. Тип Move представляет собой ход в игре. Это может быть просто целое число. В таких играх, как крестики-нолики и Connect Four, целое число представляет ход, указывая клетку или столбец, где должна быть размещена фигура. В более сложных играх для описания хода может потребоваться большее число, чем целое число. Move позволяет классу Board представлять более широкий спектр игр.

8.2. Крестики-нолики

Крестики-нолики — простая игра, но ее можно взять для иллюстрации того же минимаксного алгоритма, который применяется в сложных стратегических играх, таких как Connect Four, шашки и шахматы. Мы построим искусственный интеллект, который прекрасно играет в крестики-нолики с помощью минимаксного алгоритма.

Примечание
В этом разделе предполагается, что вы знакомы с игрой в крестики-нолики и ее стандартными правилами. Если нет, то, чуть-чуть поискав в интернете, вы найдете их.

8.2.1. Управление состоянием игры в крестики-нолики

Давайте разработаем несколько структур, позволяющих отслеживать состояние игры в крестики-нолики по мере ее развития.

Прежде всего нужен способ представления каждой клетки на игровом поле. Будем использовать перечисление TTTPiece — подкласс класса Piece. Клетка в игре в крестики-нолики может иметь значение X, 0 или быть пустой (в перечислении такие обозначаются E) (листинг 8.3).

Листинг 8.3. TTTPiece.java

package chapter8;

public enum TTTPiece implements Piece {
     X, O, E; // E — пустая клетка

     @Override
      public TTTPiece opposite() {
          switch (this) {
          case X:
              return TTTPiece.O;
          case O:
              return TTTPiece.X;
          default: // E, пустая клетка
              return TTTPiece.E;
          }
    }

    @Override
     public String toString() {
          switch (this) {
          case X:
             return "X";
          case O:
             return "O";
          default: // E, пустая клетка
             return " ";
          }
     }
}

В классе TTTPiece имеется свойство opposite, которое возвращает другой экземпляр TTTPiece. Это будет полезно для передачи хода от одного игрока к другому после того, как очередной ход игры завершен. Для представления ходов используем обычное целое число, соответствующее клетке на поле, где был поставлен крестик или нолик. Как вы помните, Move был определен в классе Board. Укажем, что Move при определении TTTPiece — целое число.

В игре в крестики-нолики существует девять позиций, образующих три ряда по три столбца. Для простоты эти девять позиций можно представить в виде одномерного списка. То, какие клетки получат какие номера (другими словами, индексы в массиве), не имеет значения, но мы будем придерживаться схемы, показанной на рис. 8.1.



Главным хранилищем состояния игры будет класс TTTBoard. Он отслеживает два элемента состояния: позицию, представленную вышеупомянутым одномерным списком, и игрока, который сейчас делает ход (листинг 8.4).

Листинг 8.4. TTTBoard.java

package chapter8;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class TTTBoard implements Board<Integer> {
    private static final int NUM_SQUARES = 9;
    private TTTPiece[] position;
    private TTTPiece turn;

    public TTTBoard(TTTPiece[] position, TTTPiece turn) {
         this.position = position;
         this.turn = turn;
    }

    public TTTBoard() {
         // по умолчанию в начале игры поле пустое
         position = new TTTPiece[NUM_SQUARES];
         Arrays.fill(position, TTTPiece.E);
        // Первый игрок ставит X
        turn = TTTPiece.X;
     }

     @Override
      public Piece getTurn() {
               return turn;
}

Исходное состояние поля — такое, при котором еще не сделано ни одного хода (пустое поле). Конструктор без параметров для TTTBoard инициализирует такую позицию, при которой первый игрок готовится поставить X (обычный первый ход в игре). getTurn() указывает, чья очередь находится в текущей позиции, X или O.

TTTBoard — это по соглашению неизменяемая структура данных: структуры TTTBoard не должны изменяться. Вместо этого каждый раз, когда необходимо сделать ход, будет генерироваться новая структура TTTBoard, позиция которой изменена с учетом хода. Впоследствии это пригодится в алгоритме поиска. При ветвлении поиска мы не сможем случайно изменить положение на поле, начиная с которого все еще анализируются потенциально возможные ходы (листинг 8.5).

Листинг 8.5. TTTBoard.java (продолжение)

@Override
public TTTBoard move(Integer location) {
          TTTPiece[] tempPosition = Arrays.copyOf(position, position.length);
          tempPosition[location] = turn;
          return new TTTBoard(tempPosition, turn.opposite());
}

Допустимым ходом в игре является любая пустая клетка. getLegalMoves() ищет любые пустые клетки на поле и возвращает их список (листинг 8.6).

Листинг 8.6. TTTBoard.java (продолжение)

@Override
public List<Integer> getLegalMoves() {
         ArrayList<Integer> legalMoves = new ArrayList<>();
         for (int i = 0; i < NUM_SQUARES; i++) {
            // пустые клетки — допустимые ходы
            if (position[i] == TTTPiece.E) {
                   legalMoves.add(i);
            }
      }
      return legalMoves;
}

Существует множество способов просмотреть строки, столбцы и диагонали на поле игры, чтобы проверить, завершилась ли она победой. В показанной далее реализации метода isWin()вместе с его вспомогательным методом checkPos() это сделано посредством жестко закодированной конструкции из &&, || и ==, которая кажется бесконечной (листинг 8.7). Это не самый красивый код, но он простой и выполняет свою работу.

Листинг 8.7. TTTBoard.java (продолжение)

@Override
public boolean isWin() {
      // проверяем три строки, три столбца и две диагонали
      return
      checkPos(0, 1, 2) || checkPos(3, 4, 5) || checkPos(6, 7, 8)
      || checkPos(0, 3, 6) || checkPos(1, 4, 7) || checkPos(2, 5, 8)
      || checkPos(0, 4, 8) || checkPos(2, 4, 6);
}
private boolean checkPos(int p0, int p1, int p2) {
     return position[p0] == position[p1] && position[p0] ==
     position[p2] && position[p0] != TTTPiece.E;
}

Если все клетки строки, столбца или диагонали не пустые и содержат одинаковые элементы, то игра выиграна.

Игра закончена вничью, если она не выиграна и не осталось допустимых ходов (это свойство уже описано в методе isDraw() класса Board). Наконец, нам нужен способ оценки конкретной позиции и структурного вывода состояния поля (листинг 8.8).

Листинг 8.8. TTTBoard.java (продолжение)

@Override
public double evaluate(Piece player) {
     if (isWin() && turn == player) {
          return -1;
     } else if (isWin() && turn != player) {
          return 1;
     } else {
          return 0.0;
     }
}

@Override
public String toString() {
      StringBuilder sb = new StringBuilder();
      for (int row = 0; row < 3; row++) {
          for (int col = 0; col < 3; col++) {
               sb.append(position[row * 3 + col].toString());
               if (col != 2) {
                    sb.append("|");
               }
           }
           sb.append(System.lineSeparator());
           if (row != 2) {
                sb.append("-----");
                sb.append(System.lineSeparator());
            }
        }
        return sb.toString();
    }
}

В большинстве игр приходится вычислять позицию приблизительно, поскольку мы не можем пройти игру до самого конца, чтобы точно определить, кто выиграет или проиграет в зависимости от того, какие ходы будут сделаны. Но в крестиках-ноликах довольно малое пространство поиска, так что мы можем пройти его от любой позиции до конца игры. Следовательно, метод evaluate() может просто возвращать некое число, если игрок выиграл, меньшее число — в случае ничьей и совсем малое — в случае проигрыша.

8.2.2. Минимакс

Минимакс — это классический алгоритм для поиска наилучшего хода в играх с двумя игроками, нулевой суммой и отличной информацией, таких как крестики-нолики, шашки или шахматы. Этот алгоритм был расширен и модифицирован для других типов игр. Минимакс обычно реализуется с использованием рекурсивной функции, в которой каждый игрок обозначается как максимизирующий или минимизирующий.

Максимизирующий игрок стремится найти ход, который приведет к максимальному выигрышу. Однако он должен учитывать ходы минимизирующего игрока. После каждой попытки максимизирующего игрока максимизировать выигрыш рекурсивно вызывается минимакс, чтобы найти ответ противника, который минимизирует максимизирующий выигрыш игрока. Это продолжается в обоих направлениях (максимизация, минимизация, максимизация и т. д.), пока не будет достигнут базовый случай рекурсивной функции. Базовый случай — это конечная позиция (выигрыш или ничья) либо достижение максимальной глубины поиска.

Минимакс вычисляет стартовую позицию для максимизирующего игрока. Для метода evaluate() класса TTTBoard, если наилучшая возможная игра обеих сторон приведет к выигрышу максимизирующего игрока, возвращается 1 балл. Если наилучшая возможная игра приведет к проигрышу, то возвращается –1. Наконец, если наилучшая игра — это ничья, то возвращается 0.

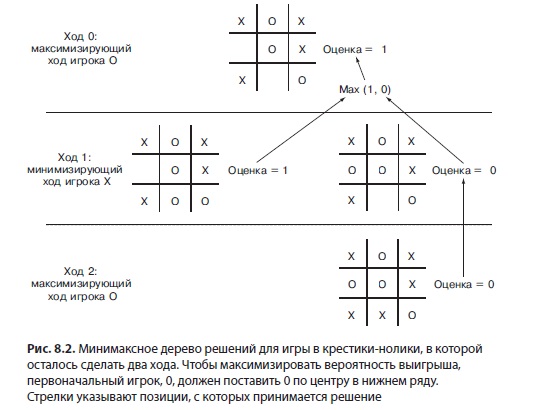
Эти числа возвращаются при достижении базового случая. Затем они передаются через все рекурсивные вызовы, которые привели к базовому случаю. Чтобы максимизировать каждый рекурсивный вызов, вверх по рекурсии передаются наилучшие вычисленные ходы. Чтобы минимизировать каждый рекурсивный вызов, передаются худшие вычисленные ходы. Таким образом строится дерево решений. На рис. 8.2 показано такое дерево, которое упрощает передачу данных вверх по рекурсивным вызовам для игры, в которой осталось сделать два хода.

В играх, имеющих слишком глубокое пространство поиска, таких как шашки и шахматы, чтобы достичь конечной позиции, минимакс останавливается после достижения определенной глубины (выполнения заданного количества ходов поиска, иногда называемого ply). Затем включается функция оценки, использующая эвристику для оценки состояния игры. Чем лучше выглядит игра для первого игрока, тем выше присуждаемая ей оценка. Мы вернемся к этой концепции, когда будем обсуждать игру Connect Four, которая имеет гораздо большее пространство поиска, чем крестики-нолики.

В листинге 8.9 представлена полная реализация функции minimax().

Листинг 8.9. Minimax.java

package chapter8;

public class Minimax {
      // Находим наилучший из возможных результатов для первого игрока
      public static <Move> double minimax(Board<Move> board,
        Boolean maximizing, Piece originalPlayer, int maxDepth) {
         // Базовый случай — достигнута финальная
         // позиция или максимальная глубина поиска
         if (board.isWin() || board.isDraw() || maxDepth == 0) {
            return board.evaluate(originalPlayer);
        }
         // Рекурсивный случай — максимизируйте свою выгоду или
         // минимизируйте выгоду противника
         if (maximizing) {
            double bestEval = Double.NEGATIVE_INFINITY; // результат выше
            for (Move move : board.getLegalMoves()) {
                double result = minimax(board.move(move), false,
                  originalPlayer, maxDepth — 1);
                bestEval = Math.max(result, bestEval);
             }
             return bestEval;
        } else { // минимизация
           double worstEval = Double.POSITIVE_INFINITY; // результат ниже
           for (Move move : board.getLegalMoves()) {
                double result = minimax(board.move(move), true,
                   originalPlayer, maxDepth — 1);
                worstEval = Math.min(result, worstEval);
          }
          return worstEval;
      }
}

При каждом рекурсивном вызове нужно отслеживать позицию на поле независимо от того, максимизируем мы ее или минимизируем и для кого пытаемся оценить позицию (originalPlayer).

Первые несколько строк функции minimax() касаются базового случая — заключительной позиции (выигрыш, проигрыш или ничья) или максимально достижимой глубины. Остальная часть функции обрабатывает рекурсивные случаи.

Один из рекурсивных случаев — это максимизация. В этой ситуации мы ищем ход, который даст максимально возможную оценку. Второй рекурсивный случай — минимизация: ищем ход, который приведет к наименьшей возможной оценке. Как бы то ни было, эти два случая чередуются, пока не будет достигнута финальная позиция или максимальная глубина поиска (базовый случай).

К сожалению, мы не можем использовать нашу реализацию minimax(), чтобы найти наилучший ход для данной позиции, так как функция возвращает оценку — значение с плавающей запятой. Оно не сообщает, какой лучший первый ход привел к данной оценке.

Вместо этого создадим вспомогательную функцию findBestMove(), которая перебирает вызовы minimax() для каждого допустимого хода из данной позиции и позволяет найти ход, который имел бы максимальную оценку. Функцию findBestMove() можно представить как первый максимизирующий вызов minimax(), но с отслеживанием начальных ходов (листинг 8.10).

Листинг 8.10. Minimax.java (продолжение)

// Найти наилучший возможный ход из текущей
// позиции, просматривая maxDepth ходов вперед
public static <Move> Move findBestMove(Board<Move> board, int maxDepth) {
     double bestEval = Double.NEGATIVE_INFINITY;
     Move bestMove = null; // Наверняка не примет значение null
     for (Move move : board.getLegalMoves()) {
        double result = minimax(board.move(move), false,
          board.getTurn(), maxDepth);
      if (result > bestEval) {
          bestEval = result;
          bestMove = move;
      }
   }
   return bestMove;
  }
}

Теперь у нас есть все необходимое, чтобы найти наилучший возможный ход для любой позиции при игре в крестики-нолики.

Более подробно с книгой можно ознакомиться на сайте издательства
» Оглавление
» Отрывок

Для Хаброжителей скидка 25% по купону — Java

По факту оплаты бумажной версии книги на e-mail высылается электронная книга.