 Привет, Хаброжители!
Привет, Хаброжители!Фундаментальные математические дисциплины, необходимые для понимания машинного обучения, — это линейная алгебра, аналитическая геометрия, векторный анализ, оптимизация, теория вероятностей и статистика. Традиционно все эти темы размазаны по различным курсам, поэтому студентам, изучающим data science или computer science, а также профессионалам в МО, сложно выстроить знания в единую концепцию.
Эта книга самодостаточна: читатель знакомится с базовыми математическими концепциями, а затем переходит к четырем основным методам МО: линейной регрессии, методу главных компонент, гауссову моделированию и методу опорных векторов.
Тем, кто только начинает изучать математику, такой подход поможет развить интуицию и получить практический опыт в применении математических знаний, а для читателей с базовым математическим образованием книга послужит отправной точкой для более продвинутого знакомства с машинным обучением.
Какова целевая аудитория книги?
Поскольку машинное обучение распространяется в обществе все шире, мы считаем, что каждый должен иметь хотя бы некоторое представление о его базовых принципах. Эта книга выдержана в академическом математическом стиле, что позволяет нам в точности описывать концепции, на которых основано МО. Читателям, не знакомым с таким, казалось бы, сухим стилем, мы рекомендуем проявить выдержку и держать в уме цель каждой рассматриваемой темы. По всему тексту рассыпаны наши комментарии и ремарки. Мы надеемся, что они послужат полезными маячками и помогут сориентироваться в общей картине.
Предполагается, что читатель обладает математическими знаниями, обычно преподаваемыми на уроках математики и физики в старших классах. Например, читатель должен иметь представление о производных и интегралах, а также о геометрических двумерных и трехмерных векторах. Отталкиваясь от данного уровня, мы обобщаем эти концепции. Следовательно, к целевой аудитории данной книги относятся студенты университетов, учащиеся вечерних курсов, слушатели онлайн-курсов по машинному обучению.
Проводя аналогию с музыкой, можно сказать, что человек может взаимодействовать с МО тремя способами:
Заинтересованный слушатель. Демократизация МО, связанная с предоставлением программного обеспечения с открытым исходным кодом для решения задач из этой области, с появлением онлайн-курсов и облачных инструментов, позволяет пользователю не вдаваться в специфику работы пайплайнов МО. Пользователь может сосредоточиться на извлечении полезной информации из данных, оперируя готовыми инструментами. Поэтому МО может пригодиться экспертам из разных предметных областей, не слишком подкованным в его технической составляющей. Ситуация подобна прослушиванию музыки: пользователь может выбирать и различать те или иные типы МО и извлекать из них что-то ценное для себя. Более опытных пользователей можно сравнить с музыкальными критиками, умеющими задавать важные вопросы о применении МО, касающиеся, например, этики, непредвзятости и неприкосновенности частной жизни индивида. Мы надеемся, что эта книга заложит основы, которые помогут задуматься о сертификации и управлении рисками при использовании систем МО и позволит экспертам из разных предметных областей, опираясь на профессиональный опыт, создавать качественные системы машинного обучения с учетом своей специализации.
Опытный исполнитель. Умелые специалисты, использующие машинное обучение на практике, могут подключать различные инструменты и библиотеки в аналитический пайплайн. Типичный практик такого рода — это дата-сайентист или инженер, понимающий интерфейсы МО, примеры их использования и умеющий выдавать великолепные прогнозы, опираясь на данные. Его можно сравнить с исполнителем-виртуозом: напрактиковавшись, такой музыкант оживляет инструмент, и его с удовольствием слушают. Воспользовавшись представленной здесь математикой как букварем, практик сможет понять пользу и ограничения любимого метода, а также расширить и обобщить существующие алгоритмы МО. Надеемся, что эта книга даст такому специалисту стимул придерживаться более строгой и последовательной разработки методов машинного обучения.
Начинающий композитор. По мере того как машинное обучение проникает в новые предметные области, разработчикам МО приходится изобретать новые методы и расширять существующие алгоритмы. Зачастую такой работой занимаются исследователи, которым необходимо понимать математический базис МО и вскрывать взаимосвязи между различными задачами. Эта работа напоминает творчество композитора, который, руководствуясь структурой и правилами теории музыки, создает новые удивительные пьесы. Надеемся, что эта книга послужит высокоуровневым обзором других технических книг для тех читателей, которые хотят заниматься МО, как композиторы — музыкой. Общество весьма нуждается в новых исследователях, способных предлагать и рассматривать новаторские подходы, позволяющие подступиться ко многим задачам, связанным с извлечением полезной информации из данных.
Предполагается, что читатель обладает математическими знаниями, обычно преподаваемыми на уроках математики и физики в старших классах. Например, читатель должен иметь представление о производных и интегралах, а также о геометрических двумерных и трехмерных векторах. Отталкиваясь от данного уровня, мы обобщаем эти концепции. Следовательно, к целевой аудитории данной книги относятся студенты университетов, учащиеся вечерних курсов, слушатели онлайн-курсов по машинному обучению.
Проводя аналогию с музыкой, можно сказать, что человек может взаимодействовать с МО тремя способами:
Заинтересованный слушатель. Демократизация МО, связанная с предоставлением программного обеспечения с открытым исходным кодом для решения задач из этой области, с появлением онлайн-курсов и облачных инструментов, позволяет пользователю не вдаваться в специфику работы пайплайнов МО. Пользователь может сосредоточиться на извлечении полезной информации из данных, оперируя готовыми инструментами. Поэтому МО может пригодиться экспертам из разных предметных областей, не слишком подкованным в его технической составляющей. Ситуация подобна прослушиванию музыки: пользователь может выбирать и различать те или иные типы МО и извлекать из них что-то ценное для себя. Более опытных пользователей можно сравнить с музыкальными критиками, умеющими задавать важные вопросы о применении МО, касающиеся, например, этики, непредвзятости и неприкосновенности частной жизни индивида. Мы надеемся, что эта книга заложит основы, которые помогут задуматься о сертификации и управлении рисками при использовании систем МО и позволит экспертам из разных предметных областей, опираясь на профессиональный опыт, создавать качественные системы машинного обучения с учетом своей специализации.
Опытный исполнитель. Умелые специалисты, использующие машинное обучение на практике, могут подключать различные инструменты и библиотеки в аналитический пайплайн. Типичный практик такого рода — это дата-сайентист или инженер, понимающий интерфейсы МО, примеры их использования и умеющий выдавать великолепные прогнозы, опираясь на данные. Его можно сравнить с исполнителем-виртуозом: напрактиковавшись, такой музыкант оживляет инструмент, и его с удовольствием слушают. Воспользовавшись представленной здесь математикой как букварем, практик сможет понять пользу и ограничения любимого метода, а также расширить и обобщить существующие алгоритмы МО. Надеемся, что эта книга даст такому специалисту стимул придерживаться более строгой и последовательной разработки методов машинного обучения.
Начинающий композитор. По мере того как машинное обучение проникает в новые предметные области, разработчикам МО приходится изобретать новые методы и расширять существующие алгоритмы. Зачастую такой работой занимаются исследователи, которым необходимо понимать математический базис МО и вскрывать взаимосвязи между различными задачами. Эта работа напоминает творчество композитора, который, руководствуясь структурой и правилами теории музыки, создает новые удивительные пьесы. Надеемся, что эта книга послужит высокоуровневым обзором других технических книг для тех читателей, которые хотят заниматься МО, как композиторы — музыкой. Общество весьма нуждается в новых исследователях, способных предлагать и рассматривать новаторские подходы, позволяющие подступиться ко многим задачам, связанным с извлечением полезной информации из данных.
Аналитическая геометрия
В главе 2 мы изучали векторы, векторные пространства и линейные отображения в общем, но абстрактном виде. В данной главе добавим к этим понятиям геометрическую интерпретацию и интуицию. В частности, рассмотрим геометрические векторы, научимся вычислять их длины, расстояния и углы между двумя векторами. Чтобы можно было это делать, определим на векторном пространстве внутреннее произведение, которое придает ему геометрические свойства. Внутренние произведения и соответствующие им нормы и метрики заключают в себе интуитивные представления о подобии и расстояниях, которыми мы воспользуемся в главе 12 при разработке машины опорных векторов. Затем нам понадобятся понятия длины вектора и угла между векторами, чтобы разобраться с ортогональными проекциями, которые будут в центре обсуждения анализа главных компонент в главе 10, а также регрессии и оценки максимального правдоподобия в главе 9. На рис. 3.1 показано, как связаны концепции из этой главы друг с другом и с материалом из других глав книги.
3.1. НОРМЫ
Рассуждая о геометрических векторах, то есть о направленных отрезках, начинающихся в начале координат, мы интуитивно понимаем, что длина вектора — это расстояние от начала координат до «конца» этого отрезка. Далее мы будем обсуждать феномен длины вектора, пользуясь понятием нормы.
Определение 3.1 (норма). Норма векторного пространства V — это функция
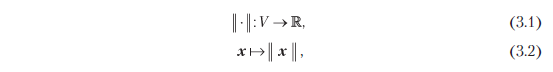
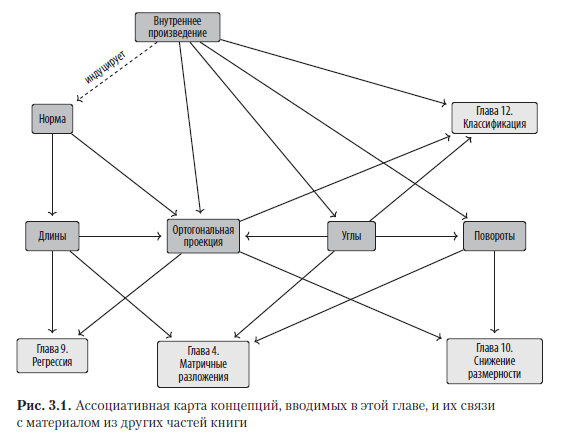
где каждому вектору x присваивается значение длины || x || ∈ R, такое что для всех λ ∈ R и x, y ∈ V соблюдается следующее:
- Абсолютная однородность: || λx || = |λ| || x ||.
- Неравенство треугольника: || x + y|| ≤ || x || + || y ||.
- Положительная определенность: || x || ≥ 0 и || x || = 0 x = 0.

В геометрических терминах неравенство треугольника постулирует, что для любого треугольника сумма длин любых двух его сторон должна быть более или равна длине третьей стороны; см. рис. 3.2 в качестве иллюстрации. Определение 3.1 дано в терминах общего векторного пространства V (раздел 2.4), но в этой книге рассматривается только конечномерное векторное пространство Rn. Помните, что для вектора x ∈ Rn элементы вектора обозначаются с использованием нижнего индекса, то есть xi — это i-й элемент вектора x.

ПРИМЕЧАНИЕ
По умолчанию в этой книге используется евклидова норма (3.4), если не указано иное.
3.2. ВНУТРЕННИЕ ПРОИЗВЕДЕНИЯ
При помощи внутренних произведений (внутренним называется произведение одного вектора на другой) удобно ввести интуитивно понятные геометрические концепции, в частности длину вектора и угол или расстояние между двумя векторами. Главное назначение внутренних произведений — определять, ортогональны ли векторы друг другу.
3.2.1. Скалярное произведение
Возможно, вам уже известно об особом типе внутреннего произведения, скалярном произведении Rn, которое записывается как
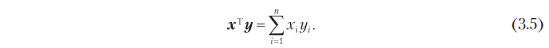
Такой частный случай внутреннего произведения мы будем называть в этой книге скалярным. Но концепция внутренних произведений более общая, и внутренние произведения обладают специфическими свойствами, о которых мы сейчас расскажем.
3.2.2. Общие внутренние произведения
Вспомните линейное отображение из раздела 2.7, где было показано, как можно переупорядочить отображение при сложении и умножении на скаляр. Билинейное отображение Ω — это отображение с двумя аргументами, и в каждом аргументе оно линейно, то есть при рассмотрении векторного пространства V для всех x, y, z ∈ V, λ, ψ ∈ R верно, что
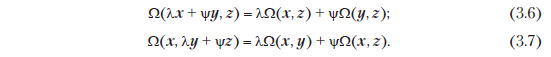
Здесь в (3.6) утверждается, что Ω линейно в первом аргументе, а в (3.7) утверждается, что Ω линейно во втором аргументе (см. также (2.87)).
Определение 3.2. Пусть V — векторное пространство, а Ω: V × V → R билинейное отображение, которое принимает два вектора и отображает их на вещественное число. Тогда
- Ω называется симметричным, если Ω(x, y) = Ω(y, x) для всех x, y ∈ V, то есть порядок следования аргументов не важен.
- Ω называется положительно определенным, если
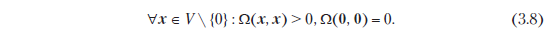
Определение 3.3. Пусть V — векторное пространство, а Ω: V × V → R билинейное отображение, которое принимает два вектора и отображает их на вещественное число. Тогда:
- Положительно определенное, симметричное билинейное отображение Ω: V × V → R называется внутренним произведением V. Как правило, пишут <x, y>, а не Ω(x, y).
- Пара (V, <·, ·>) называется предгильбертовым пространством или (вещественным) векторным пространством с внутренним произведением. Если воспользоваться скалярным произведением, определенным в (3.5), то (V, <, ·>) называется евклидовым векторным пространством.
Такие пространства в этой книге будут называться предгильбертовыми пространствами.

3.2.3. Симметричные положительно определенные матрицы
Симметричные положительно определенные матрицы играют важную роль в машинном обучении. Они определяются при помощи внутреннего произведения. В разделе 4.3 мы вернемся к симметричным положительно определенным матрицам в контексте разложения матриц. Идея симметричных положительно полуопределенных матриц играет ключевую роль при определении ядер (раздел 12.4).
Рассмотрим n-мерное векторное пространство V с внутренним произведением <·, ·>: V × V → R (см. определение 3.3) и упорядоченным базисом B = (b1, ..., bn) от V. Как вы помните из раздела 2.6.1, любые векторы x, y ∈ V можно записать как линейную комбинацию базисных векторов, такую что
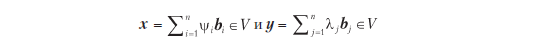
для подходящих ψiλj ∈ R. Поскольку внутреннее произведение билинейно, для всех x, y ∈ V верно, что
Поскольку внутреннее произведение билинейно, для всех x, y ∈ V верно, что
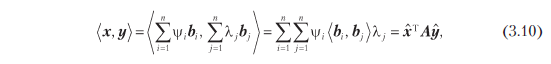
где
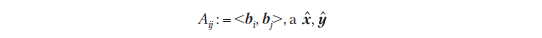
— это координаты x и y относительно базиса B. Это подразумевает, что внутреннее произведение <·, ·> уникально определяется через A.
Симметрия внутреннего произведения также означает, что A симметрично. Кроме того, положительная определенность внутреннего произведения подразумевает, что
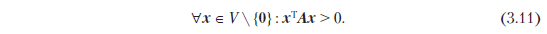
Определение 3.4 (симметричная, положительно определенная матрица). Симметричная матрица A ∈ Rn × n, удовлетворяющая (3.11), называется симметричной, положительно определенной или просто положительно определенной. Если для (3.11) верно только ≥, то A называется симметричной, положительно полуопределенной.

Если A ∈ Rn × n симметрична, положительно определенна, то
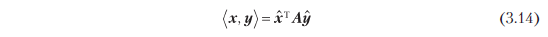
определяет внутреннее произведение относительно упорядоченного базиса B, где и — координатные представления x, y ∈ V относительно B.
Теорема 3.5. Для вещественнозначного, конечномерного векторного пространства V и упорядоченного базиса B от V верно, что <·, ·>: V × V → R является внутренним произведением тогда и только тогда, если существует симметричная, положительно определенная матрица A ∈ Rn × n с
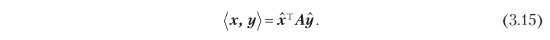
Следующие свойства соблюдаются, если A ∈ Rn × n является симметричной и положительно определенной:
- Нулевое пространство (ядро) A состоит лишь из 0, поскольку xT Ax > 0 для всех x ≠ 0. Это подразумевает, что Ax ≠ 0 и x ≠ 0.
- Диагональные элементы aii от A положительны, поскольку aii = eiT Aei > 0, где ei это i-й вектор стандартного базиса в Rn.
3.3. ДЛИНЫ И РАССТОЯНИЯ
В разделе 3.1 мы уже обсуждали нормы, которыми можно пользоваться для вычисления длины вектора. Внутренние произведения и нормы тесно связаны в том смысле, что любое внутреннее произведение вводит норму
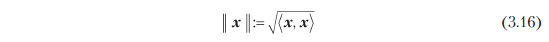
естественным образом, так что длины векторов можно вычислять при помощи внутреннего произведения. Но не всякая норма вводится внутренним произведением. Манхэттенская норма (3.3) — такая, у которой нет соответствующего внутреннего произведения. В дальнейшем мы сосредоточимся на нормах, вводимых внутренними произведениями, и познакомимся с геометрическими концепциями, в частности с длинами, расстояниями и углами.
ПРИМЕЧАНИЕ
Для векторного пространства внутреннего произведения (V,<·, ·>) индуцированная норма || · || удовлетворяет неравенству Коши — Шварца
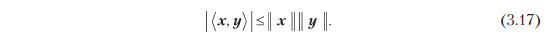

Определение 3.6 (расстояние и метрика). Рассмотрим пространство внутреннего произведения (V,<·, ·>). Тогда
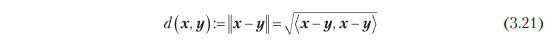
называется расстоянием между x и y для x, y ∈ V. Если использовать скалярное произведение как внутреннее, то это расстояние называется евклидовым расстоянием. Отображение
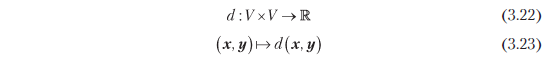
называется метрикой.
ПРИМЕЧАНИЕ
Подобно длине вектора, расстояние между векторами не требует внутреннего произведения; достаточно нормы. Если у вас есть норма, индуцированная внутренним произведением, то расстояние может отличаться в зависимости от выбранного внутреннего произведения.
Метрика d удовлетворяет следующим условиям:
1. d является положительно определенной, то есть d(x, y) ≥ 0 для всех x, y ∈ V и d(x, y) = 0 x = y.
2. d симметрично, то есть d(x, y) = d(y, x) для всех x, y ∈ V.
3. Неравенство треугольников: d(x, z) ≤ d(x, y) для всех x, y, z ∈ V.
ПРИМЕЧАНИЕ
На первый взгляд, списки свойств внутренних произведений и метрик выглядят очень похоже. Однако если сравнить определение 3.3 с определением 3.6, то можно заменить, что <x, y> и d(x, y) действуют в противоположных направлениях. Очень схожие x и y будут давать большое значение для внутреннего произведения и малое значение для метрики.
3.4. УГЛЫ И ОРТОГОНАЛЬНОСТЬ
Внутренние произведения позволяют не только определять длины векторов и расстояние между двумя векторами, но и схватывают геометрию векторного пространства, определяя угол ω между двумя векторами. Мы воспользуемся неравенством Коши — Шварца (3.17) для определения углов ω в пространствах внутренних произведений между двумя векторами x, y, и это определение совпадает с интуитивным пониманием R2 и R3. Предположим, что x ≠ 0, y ≠ 0. Тогда
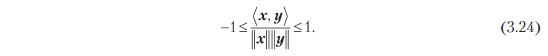
Следовательно, существует уникальный ω ∈ [0, π], показанный на рис. 3.4, с

Число ω — это угол между векторами x и y. Интуитивно понятно, что угол между двумя векторами позволяет судить, насколько схоже они ориентированы. Например, воспользовавшись скалярным произведением, найдем, что угол между x и y = 4x (то есть y — это x с некоторым множителем) равен 0.

Определение 3.7 (ортогональность). Два вектора x и y ортогональны тогда и только тогда, когда <x, y> = 0, и мы пишем x _|_ y. Если к тому же || x || = 1 = || y ||, то есть векторы являются единичными, то x и y ортонормированны.
Из этого определения следует, что 0-вектор ортогонален любому вектору в векторном пространстве.
ПРИМЕЧАНИЕ
Ортогональность — это обобщение концепции перпендикулярности, применимой к билинейным формам, которые не обязательно дают скалярное произведение. В нашем контексте с геометрической точки зрения можно считать, что ортогональные векторы расположены под прямым углом относительно конкретного внутреннего произведения.

Определение 3.8 (ортогональная матрица). Квадратная матрица A ∈ Rn × n является ортогональной матрицей тогда и только тогда, когда ее столбцы ортонормированны, так что
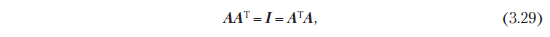
что подразумевает
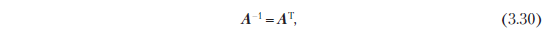
то есть обратная матрица получается простым транспонированием матрицы.
Преобразования ортогональных матриц представляют особенный случай, поскольку длина вектора x не меняется, если преобразовывать его с применением ортогональной матрицы A. Для скалярного произведения получаем
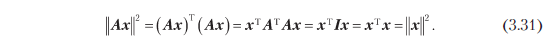
Более того, угол между любыми двумя векторами x, y, измеренный по их внутреннему произведению, также не изменится, если преобразовать оба эти вектора с применением ортогональной матрицы A. Взяв скалярное произведение в качестве внутреннего, получим, что угол образов Ax и Ay дается как
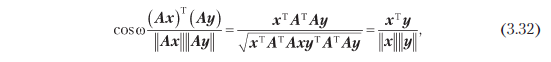
то есть в точности равен углу между x и y. Это означает, что у ортогональных матриц A, где AT = A–1, сохраняются как углы, так и расстояния. Оказывается, что ортогональные матрицы определяют преобразования, являющиеся поворотами (с возможностью переворота). В разделе 3.9 мы подробнее поговорим о поворотах.
Более подробно с книгой можно ознакомиться на сайте издательства:
» Оглавление
» Отрывок
По факту оплаты бумажной версии книги на e-mail высылается электронная книга.
Для Хаброжителей скидка 25% по купону — Математика






