В данной статье мы рассмотрим понятие моноид и узнаем, как он может помочь нам при сортировке данных.
Интересующихся функциональным программированием на Kotlin также приглашаю заглянуть на мой youtube-канал, где я разбираю разные интересные моменты из Kotlin FP.

Моноид — простая, но удивительно мощная концепция, которая определяется как множество с бинарной операцией. Всё, что требуется от операции — ассоциативность и наличие специального нейтрального элемента.
Например, натуральные числа с операцией сложения и элементом “ноль” образуют моноид.
Ассоциативность — это свойство, при котором результат последовательного применения операций не зависит от расстановки скобок:
Другими словами, при сложении чисел мы можем опустить скобки.
Нейтральный элемент — ноль, поскольку:
Многие примитивные типы являются моноидом.
Например:
Натуральные числа с операцией умножения и нейтральным элементом “1”
Строки с операцией конкатенации (склеивания) и нейтральным элементом “” (пустой строкой)
Возьмем функцию, у которой принимаемый тип равен возвращаемому:
Эта функция с операцией композиции является моноидом.
Прежде чем рассматривать моноид, предлагаю вспомнить, что такое композиция функций.
Допустим, у нас есть две функции.
Первая принимает аргумент A и возвращает значения типа B:
Вторая принимает аргумент B и возвращает значения типа С:
Из этих двух функций мы можем создать третью, которая принимает аргумент A
и возвращает значения типа С:
Это преобразование и есть композиция функций.
Реализация композиции функций:
Ассоциативность композиции довольно очевидна:
Нейтральным элементом для операции композиции будет являться функция identity:
То есть такая функция, которая возвращает значение, принятое на входе.
Доказательство того, что identity является нейтральным элементом так же очевидно:
Теперь вновь вернемся к функции
Так как композиция подобных функций является бинарной операцией,
а композиция ассоциативна и имеет нейтральный элемент, то функция
(A) -> A является моноидом.
Далее рассмотрим функцию:
где B — это моноид (т.е. область значения функции является моноидом).
Такая функция с бинарной операцией
будет также являться моноидом.
Для примера рассмотрим функцию:
Ранее мы рассмотрели, что множество значений типа Int с бинарной операцией сложения — это моноид.
А для функции (A) -> Int мы можем написать бинарную операцию:
Ассоциативность которой прослеживается из Int и нейтральным элементом является функция, возвращающая нейтральный элемент для Int, то есть:
Функции моноиды нам пригодятся на практике, к которой мы сейчас перейдем.
Создадим интерфейс моноида:
Он содержит две функции:
Создадим enum-класс, который содержит в себе значения, соответствующие типу отношений между объектами (больше, меньше, либо равно):
Допустим, у нас имеется класс пользователя User с полями name и age.
Перед нами стоит задача сравнить двух пользователей user1 и user2.
Мы можем сравнить имена пользователей и получить значение Order, показывающее тип отношений между ними.
Также мы можем сравнить возраст пользователей и получить соответствующее значение Order.
В обычной ситуации сначала мы сравниваем имена пользователей.
Если они не равны, возвращаем результат сравнения имен.
Если же имена равны, то возвращаем результат сравнения возрастов:
Как мы видим, данная операция является бинарной. Из значений Order, которые мы получили при сравнении имен пользователей, а затем их возрастов, мы получаем итоговое значение Order, показывающее отношение объектов класса User.
Order с такой бинарной операцией является моноидом.
Ассоциативность в данном случае хорошо прослеживается:
Так как не важен порядок скобок, наибольший приоритет будет иметь order, стоящий в операции левее остальных.
И нейтральный элемент EQ, который соответствует правилу:
Следующим шагом рассмотрим функцию:
Она также является моноидом, так как область значения этой функции — моноид.
Реализация:
В Kotlin мы можем сравнивать основные типы (String, Int, Float, ...), потому что они наследуются от интерфейса Comparable. Из этого следует, что мы можем написать функцию получения Order для основных типов Kotlin:
Также мы сможем получать наш ComparatorMonoid из функции, возвращающей значение типа Comparable:
Теперь научим списки работать с ComparatorMonoid:
В итоге мы получили следующее:
Теперь давайте воспользуемся этим.
Создадим класс User и необходимый для него класс Address:
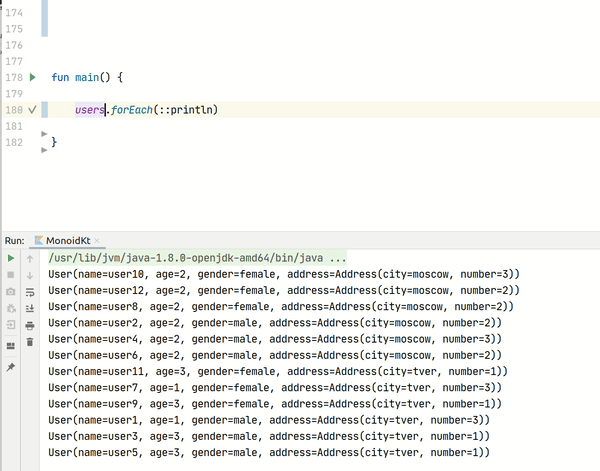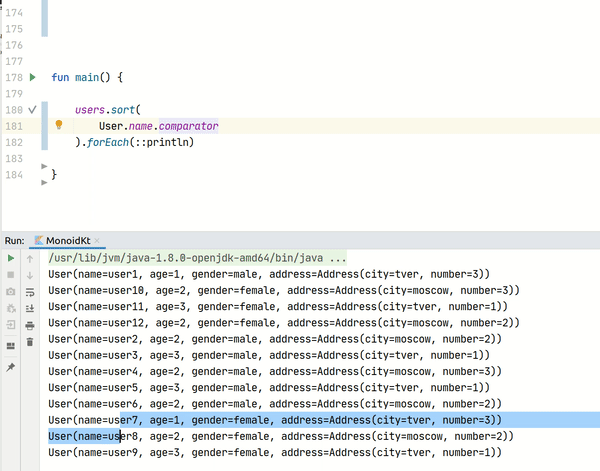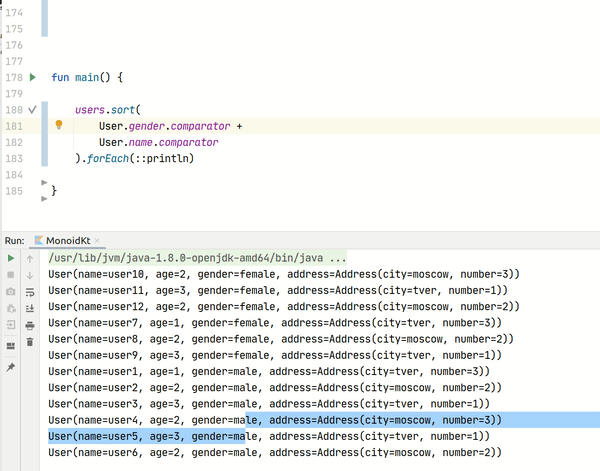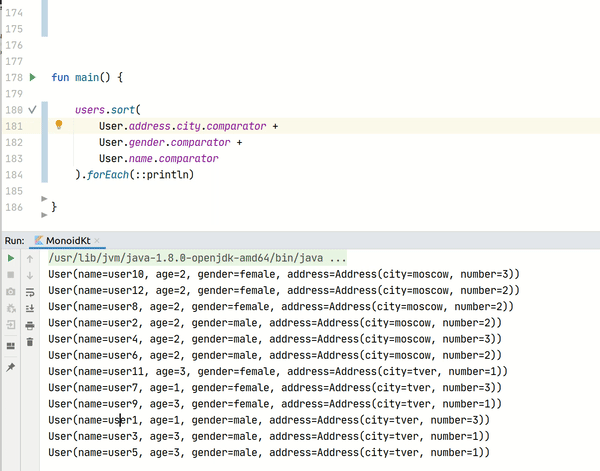
Создадим тестовые данные:
Теперь мы можем сортировать этот список по любым полям и в любой последовательности, в которой нам нужно.
К примеру, у нас стоит задача произвести сортировку сначала по возрасту, затем по имени. Решается она следующим образом:
Если нам необходима сортировка пользователей по названию города, которое содержится в поле city класса Address, а затем по полу (gender), а после него ещё и по имени (name), то функция будет выглядеть следующим образом:
Как мы видим, с помощью моноида мы можем удобно сортировать данные, основываясь на доказательной базе теории категорий.
Также улучшить реализацию данного механизма сортировок можно с помощью Lens, и тогда он станет выглядеть следующим образом:
Lens и многие другие интересные, на мой взгляд, моменты из функционального программирования уже рассмотрены и будут рассматриваться дальше на моём youtube-канале
Интересующихся функциональным программированием на Kotlin также приглашаю заглянуть на мой youtube-канал, где я разбираю разные интересные моменты из Kotlin FP.

Теория
Моноид — простая, но удивительно мощная концепция, которая определяется как множество с бинарной операцией. Всё, что требуется от операции — ассоциативность и наличие специального нейтрального элемента.
Например, натуральные числа с операцией сложения и элементом “ноль” образуют моноид.
Ассоциативность — это свойство, при котором результат последовательного применения операций не зависит от расстановки скобок:
Другими словами, при сложении чисел мы можем опустить скобки.
Нейтральный элемент — ноль, поскольку:
Многие примитивные типы являются моноидом.
Например:
Натуральные числа с операцией умножения и нейтральным элементом “1”
Строки с операцией конкатенации (склеивания) и нейтральным элементом “” (пустой строкой)
Теперь перейдем к функциям.
Возьмем функцию, у которой принимаемый тип равен возвращаемому:
Эта функция с операцией композиции является моноидом.
Прежде чем рассматривать моноид, предлагаю вспомнить, что такое композиция функций.
Допустим, у нас есть две функции.
Первая принимает аргумент A и возвращает значения типа B:
Вторая принимает аргумент B и возвращает значения типа С:
Из этих двух функций мы можем создать третью, которая принимает аргумент A
и возвращает значения типа С:
Это преобразование и есть композиция функций.
Реализация композиции функций:
infix fun <A, B, C> ((A) -> B).andThen(g: (B) -> C): (A) -> C = { a: A ->
g(this(a))
}
Ассоциативность композиции довольно очевидна:
val f: (A) -> B
val g: (B) -> C
val h: (C) -> D
f andThen g andThen h == f andThen (g andThen h) == (f andThen g) andThen h
Нейтральным элементом для операции композиции будет являться функция identity:
fun <T> identity(x: T): T = xТо есть такая функция, которая возвращает значение, принятое на входе.
Доказательство того, что identity является нейтральным элементом так же очевидно:
f andThen ::identity = f = ::identity andThen f
Теперь вновь вернемся к функции
Так как композиция подобных функций является бинарной операцией,
а композиция ассоциативна и имеет нейтральный элемент, то функция
(A) -> A является моноидом.
Далее рассмотрим функцию:
где B — это моноид (т.е. область значения функции является моноидом).
Такая функция с бинарной операцией
будет также являться моноидом.
Для примера рассмотрим функцию:
Ранее мы рассмотрели, что множество значений типа Int с бинарной операцией сложения — это моноид.
А для функции (A) -> Int мы можем написать бинарную операцию:
operator fun <A> ((A) -> Int).plus(g: (A) -> Int) = { a: A -> this(a) + g(a) }Ассоциативность которой прослеживается из Int и нейтральным элементом является функция, возвращающая нейтральный элемент для Int, то есть:
val f: (A) -> Int = { 0 }Функции моноиды нам пригодятся на практике, к которой мы сейчас перейдем.
Практика
Создадим интерфейс моноида:
interface Monoid<A> {
operator fun plus(rh: A): A
fun empty(): A
}
Он содержит две функции:
- plus — ассоциативная бинарная операция
- empty — нейтральный элемент для функции plus
Создадим enum-класс, который содержит в себе значения, соответствующие типу отношений между объектами (больше, меньше, либо равно):
enum class Order(val compareValue: Int) {
LT(-1),
EQ(0),
GT(1)
}
Допустим, у нас имеется класс пользователя User с полями name и age.
Перед нами стоит задача сравнить двух пользователей user1 и user2.
Мы можем сравнить имена пользователей и получить значение Order, показывающее тип отношений между ними.
Также мы можем сравнить возраст пользователей и получить соответствующее значение Order.
В обычной ситуации сначала мы сравниваем имена пользователей.
Если они не равны, возвращаем результат сравнения имен.
Если же имена равны, то возвращаем результат сравнения возрастов:
fun plus(nameOrder: Order, ageOrder: Order) = when(nameOrder) {
LT -> LT
EQ -> ageOrder
GT -> GT
}
Как мы видим, данная операция является бинарной. Из значений Order, которые мы получили при сравнении имен пользователей, а затем их возрастов, мы получаем итоговое значение Order, показывающее отношение объектов класса User.
Order с такой бинарной операцией является моноидом.
enum class Order(val compareValue: Int) : Monoid<Order> {
LT(-1),
EQ(0),
GT(1);
override fun plus(rh: Order) = when (this) {
LT -> LT
EQ -> rh
GT -> GT
}
override fun empty() = EQ
}
Ассоциативность в данном случае хорошо прослеживается:
Так как не важен порядок скобок, наибольший приоритет будет иметь order, стоящий в операции левее остальных.
И нейтральный элемент EQ, который соответствует правилу:
Следующим шагом рассмотрим функцию:
Она также является моноидом, так как область значения этой функции — моноид.
Реализация:
fun interface ComparatorMonoid<A> : Monoid<ComparatorMonoid<A>> {
fun compare(a: A, other: A): Order
override fun plus(rh: ComparatorMonoid<A>) =
ComparatorMonoid<A> { a, other -> compare(a, other) + rh.compare(a, other) }
override fun empty() = ComparatorMonoid<A> { _, _ -> Order.EQ }
}
В Kotlin мы можем сравнивать основные типы (String, Int, Float, ...), потому что они наследуются от интерфейса Comparable. Из этого следует, что мы можем написать функцию получения Order для основных типов Kotlin:
fun <A : Comparable<A>> A.compare(other: A) = when {
this > other -> Order.GT
this == other -> Order.EQ
else -> Order.LT
}
Также мы сможем получать наш ComparatorMonoid из функции, возвращающей значение типа Comparable:
val <A, B : Comparable<B>> ((A) -> B).comparator
get():ComparatorMonoid<A> = ComparatorMonoid<A> { a, b ->
invoke(a).compare(invoke(b))
}
Теперь научим списки работать с ComparatorMonoid:
fun <A> Iterable<A>.sort(comparatorMonoid: ComparatorMonoid<A>) =
sortedWith { a, b -> comparatorMonoid.compare(a, b).compareValue }
В итоге мы получили следующее:
- Списки, которые умеют сортироваться на основе ComparatorMonoid;
- ComparatorMonoid, который умеет комбинироваться на основании того, что он является моноидом;
- ComparatorMonoid можно получить из Kotlin Comparable.
Теперь давайте воспользуемся этим.
Создадим класс User и необходимый для него класс Address:
data class User(val name: String, val age: Int, val gender: String, val address: Address)
data class Address(val city: String, val number: Int)
Создадим тестовые данные:
val users: List<User>
Теперь мы можем сортировать этот список по любым полям и в любой последовательности, в которой нам нужно.
К примеру, у нас стоит задача произвести сортировку сначала по возрасту, затем по имени. Решается она следующим образом:
users.sort(User::age.comparator + User::name.comparator)
Если нам необходима сортировка пользователей по названию города, которое содержится в поле city класса Address, а затем по полу (gender), а после него ещё и по имени (name), то функция будет выглядеть следующим образом:
users.sort(
User::address.andThen(Address::city).comparator +
User::gender.comparator +
User::name.comparator
)
Как мы видим, с помощью моноида мы можем удобно сортировать данные, основываясь на доказательной базе теории категорий.
Также улучшить реализацию данного механизма сортировок можно с помощью Lens, и тогда он станет выглядеть следующим образом:
users.sort(
User.address.city.comparator +
User.gender.comparator +
User.name.comparator
)

Lens и многие другие интересные, на мой взгляд, моменты из функционального программирования уже рассмотрены и будут рассматриваться дальше на моём youtube-канале