
Данный пост является продолжением ранее опубликованного поста «Квантовая запутанность глазами хакера. Часть 1», где рассматривались теоретические трудности, не позволяющие построить коммуникацию с использованием квантовой запутанности. В ходе анализа экспериментальных схем были сформированы важные выводы, которые играют ключевую роль для понимания существующих ограничений и построения методов их решения. Поэтому, настоятельно рекомендую ознакомиться с первой частью данного поста, если вы этого еще не сделали. В этой части мы вплотную перейдем к практической части наших исследований.
Ранее нам удалось построить схему квантового ластика с возможностью восстановления информации. Полученная схема позволило определить ось измерения запутанных пар при наличии трех возможных состояний поляризации. Но к сожалению, нам не удалось получить необходимые квантовые состояния запутанных пар.
Исходя из проведенных экспериментов можно сделать вывод, что данную задачу невозможно решить используя только интерференцию. Потребуется применение дополнительного физического явления. Попробуем подойти к решению задачи с другой стороны.
4-Х ЩЕЛЕВОЙ ЭКСПЕРИМЕНТ НА ДИФРАКЦИОННОЙ РЕШЕТКЕ
Рассмотрим 4-х щелевой эксперимент на дифракционной решетке. На каждой щели расположены линейные поляризаторы, направления которых чередуются. Фотоны, обладающие горизонтальной поляризацией способны пройти через щели 1 и 3, а фотоны, обладающие вертикальной поляризацией способны пройти через щели 2 и 4. Схема эксперимента выглядит следующим образом:
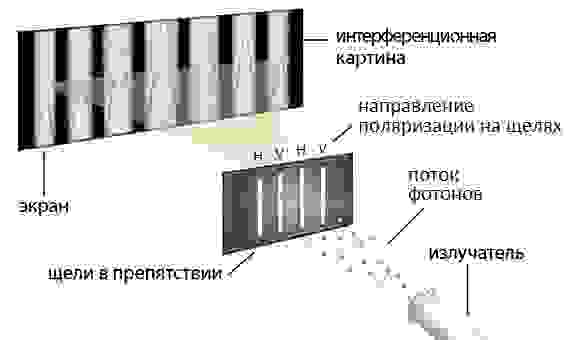
Суть эксперимента состоит в следующем: если фотоны обладают горизонтальной либо вертикальной поляризацией, то в обоих случаях возникает суперпозиция между двумя щелями, создавая на экране картину двухщелевой интерференции. А если фотоны обладают поляризацией (H+V) и (H—V), то в суперпозиции участвуют все 4 щели. В последнем случае мы получаем не просто интерференцию, а 4-х щелевую дифракцию.
Главным параметром дифракционной решетки является ее период (d), которая равная:
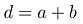
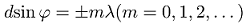
при уменьшении периода (d) в два раза, количество наблюдаемых максимумов на экране также должно сократиться в два раза. Это означает, что если фотоны обладают поляризацией по оси (H+V) и (H—V), то мы должны получить на экране два раза меньше максимумов, чем если бы фотоны обладали поляризацией по оси H и V. Но чтобы получить поляризацией фотонов по оси (H+V) и (H—V) придется выполнить квантовое стирание с помощью запутанных пар, или же провести квантовое стирание локально, путем размещения перед экраном линейного поляризатора по диагонали. Мы выберем второй вариант, чтобы проверить на практике результаты данного эксперимента:

При вращении линейного поляризатора видно, что количество максимумов для состояний (H+V) и (H—V) действительно 2 раза меньше, чем количество максимумов для H и V. Но поскольку максимумы H и V накладываются друг на друга, то состояния (H+V) и (H—V) в сумме дают такое же количество максимумов на экране. Из этого следует, что при любых направлениях измерения квантово-запутанных пар интерференционная картина на экране будет совершенно одинаковым.
Можно предположить, что причиной этого является равные условия прохождения фотонов H и V через дифракционную решетку. Попробуем создать неравные условия прохождения для фотонов обладающих горизонтальную или вертикальную поляризацию.
3-Х ЩЕЛЕВОЙ ЭКСПЕРИМЕНТ НА ДИФРАКЦИОННОЙ РЕШЕТКЕ
Рассмотрим 3-х щелевой эксперимент на дифракционной решетке. На каждой щели расположены линейные поляризаторы, направления которых чередуются. Фотоны, обладающие горизонтальной поляризацией способны пройти через щели 1 и 3, а фотоны, обладающие вертикальной поляризацией способны пройти только через 2-ю щель. При этом на выходе 2-й щели установлена пластина с нематическими жидкими кристаллами, которое поворачивает направление линейной поляризации на 90°. Это позволяет получить на выходе одинаковое направление линейной поляризации из всех трёх щелей. Схема эксперимента выглядит следующим образом:

Суть данного эксперимента состоит в следующем: для фотонов, обладающих горизонтальной поляризацией на экране возникнет картина двухщелевой интерференции, а для фотонов с вертикальной поляризацией интерференции не будет. Если же фотоны будут обладать поляризацией (H+V) и (H—V), то на экране должна возникнуть картина 3-щелевой дифракции, которая отличается от картины двущелевой интерференции. В последнем случае мы предполагаем увидеть следующую картину дифракции на 3-х щелях:
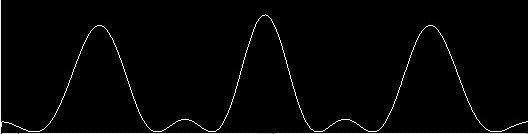
Попробуем провести реальный эксперимент и посмотрим на полученные результаты. Фотоны, обладающие горизонтальной поляризацией, как и следовало ожидать, создают на экране картину двухщелевой интерференции:

А фотоны обладающие поляризацией (H+V) по какой-то причине дают совершенно не ту картину 3-х щелевой дифракции, которую мы ожидали увидеть:

В чем причина возникновения такой картины? Несмотря на то, что мы имеем одинаковое направление линейной поляризации на выходе каждой щели, разворот вертикальной поляризации на 90° привело к тому, что волны складываются совершенно иначе, чем при 3-х щелевой дифракции. После долгих раздумий была сформирована следующая гипотеза: 2-я щель оказывает такое воздействие, при котором, волны, которые должны были гасить друг друга, напротив усиливаются, а волны которые должны усиливать друг друга, гасят друг друга. В результате мы получаем инвертированную 3-х щелевую дифракцию, в котором вместо минимумом возникают максимумы, а в место максимумов возникают минимумы:
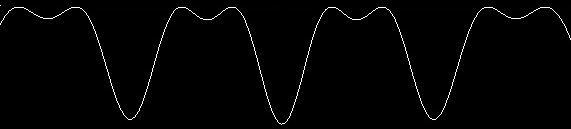
Небольшие минимумы в центре каждого максимума тоже отчетливо видны в эксперименте невооруженным глазом, хотя на фотографию они не попали (к сожалению, фотокамера имеет меньший динамический диапазон по сравнению с человеческим глазом, и дает равномерную засветку дифракционных максимумов).
В процессе наших поисков мы, по всей видимости, обнаружили новое явление в квантовой механике, как «инвертированная дифракция», которое ранее не описывалось в научной литературе, и возможно, еще не изучена официальной наукой. Мне трудно сказать какую волновую функцию будет иметь данное явление, думаю, физики в этом разберутся. Но мы же перейдем к следующему шагу, поскольку у нас несколько другая задача.
Далее нам нужно выяснить, как измениться картина на экране, если фотоны на входе будут в равной степени обладать поляризацией (H+V) и (H—V). Возьмем кулер от корпуса ПК и прикрепим к нему диск с большим количеством отверстии. На эти отверстия установим поляризационные плёнки с чередующимися направлениями линейной поляризации. Вращение кулера с высокой скоростью приведет к чередованию линейной поляризации (H+V) и (H—V) на входе дифракционной решетки. В результате мы увидим на экране наложение дифракционных максимумов для начальных состояний (H+V) и (H—V), которые будут имеют фазовый сдвиг друг относительно друга следующим образом:

В процессе такого наложения возникают более интенсивные и менее интенсивные участки максимумов и минимумов, которые становятся неотличимы от двухщелевой интерференции фотонов с поляризации H, и равномерного распределения фотонов с поляризацией V.
Как видим, квантовая механика нашла весьма оригинальный способ выкрутиться из создавшегося положения. Вращение поляризации на одной из щелей привело к неожиданным последствиям, в виде «инвертированной дифракции» и нарушило наши планы. А можно ли обойти эти трудности? Что нам мешает провести чистый 3-х щелевой эксперимент, без какого либо измерения и вращения поляризации на щелях? Пусть фотоны, как говориться, сами выбирают, через какую щель им проходит. Немного перефразировав, мы получим постановку задачи для следующего эксперимента: необходимо создать такие условия, при котором фотоны, в зависимости от квантовых состояний, должны проходить через ту или иную щель, которую мы считаем необходимым, не производя при этом никакого измерения или преобразования их квантового состояния на дифракционной решетке. Звучит безумно, но поскольку мы уже привыкли решать такие задачи, то постараемся решить и эту.
3-Х ЩЕЛЕВОЙ ЭКСПЕРИМЕНТ С ЗАДАННЫМИ НАЧАЛЬНЫМИ УСЛОВИЯМИ
Для создания начальных условий воспользуемся схемой эксперимента «квантового ластика с возможностью восстановления информации», которую мы подробно рассматривали в предыдущей части нашей статьи. Только вместо интерферометра мы будем использовать двухщелевую пластину, с установленными поляризаторами H и V на каждой щели. На выходе второй щели мы также установим пластину с нематическими жидкими кристаллами, чтобы развернуть вертикальную поляризацию на 90°. Это позволит получить интерференцию для начальных состояний (H+V) и (H—V). Состояния H и V при этом будут проходить только через одну из двух щелей.
На определенном расстояние от первой пластины с препятствиями мы расположим вторую пластину, на котором уже будут расположены три щели. Схема эксперимента будет выглядеть следующим образом:
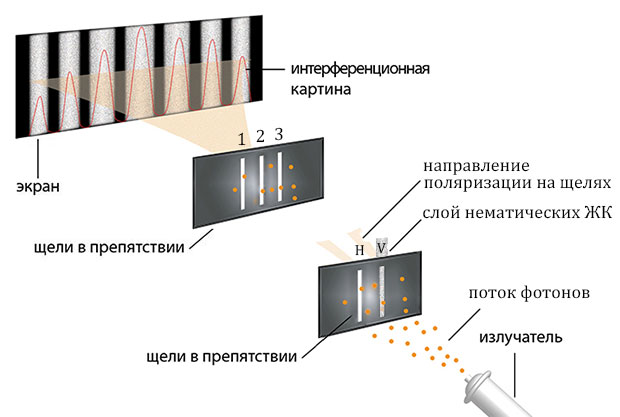
Расстояние между щелями на второй пластине выберем таким образом, чтобы интерференционные максимумы начального состояния (H+V) могли пройти только через 1 и 3 щель. А интерференционные максимумы состояния (H—V) могли проходить только через 2-ю щель. Соответственно, для фотонов обладающих начальной поляризацией (H+V) на экране возникнет картина двухщелевой интерференции, а для фотонов с поляризацией (H—V) интерференции не будет.
Поскольку состояния H и V не создают интерференции при прохождении первой пластины, то во второй пластине с препятствиями они смогут проходить через все 3 щели, создавая картину 3-х щелевой дифракции. Следует отметить, что при прохождении каждой щели фотоны уже не подвергаются никаким измерениям и преобразованиям их квантовых состояний, а значит, подчиняются к классическим законам дифракции. Соответственно, для фотонов с начальной поляризацией H мы получим на экране привычную картину 3-х щелевой дифракции:

Фотоны с начальной поляризацией V также будут иметь привычную картину 3-х щелевой дифракции, но при этом будут иметь фазовый сдвиг на половину периода волны, поскольку будут проходить из другой щели на первой пластине. Наложение дифракционных максимумов для начальных состояний H и V согласно расчетам будет выглядеть следующим образом:

Как видим, наложение двух максимумов приводит к тому, что полученная картина не отличается от картины двухщелевой интерференции, когда фотоны имели поляризацию (H+V). Но есть существенное отличие — фотоны с начальной поляризацией (H—V) равномерно распределялись по экрану, поскольку проходили через одну щель и не могли интерферировать. В данном случае мы видим очень чёткие минимумы, в которых фотоны почти не попадают. Это является следствием неравенства для разных направлений поляризации, которую мы пытались достичь.
Не трудно догадаться, что если бы существовала вторая щель для прохождения фотонов (H—V), то картина стала бы неотличима при любых направлениях начальной поляризации (поскольку не имела бы равномерного распределения фотонов по экрану). Заставив фотоны (H—V) проходить только через одну щель мы нарушили возможность возникновения интерференции для одной из направлений поляризации.
В результате, по интенсивности попадания фотов в интерференционные минимумы можно будет определить, в каком базисе Алиса измерила свою часть запутанных пар. В одном случае их будет больше, а в другом случае меньше. Если экспериментальные результаты совпадут с представленными теоретическими расчетами, то это будет означать, что квантовая запутанность все же позволяет передавать информацию. Но мне, к сожалению, пока не удалось провести последний эксперимент, так что буду рад, если кто-нибудь сможет провести данный эксперимент и поделиться своими результатами.
Думаю, мы смогли решить поставленную задачу и перевести теоретически невыполнимую задачу в плоскость практически наблюдаемых экспериментальных данных. А значит, смогли подобрать правильные ключи к тайнам этого удивительного мира, открывающие невероятные возможности для коммуникации, телепортации и различных других задач.






