
«Наша [Ирвинга Капланского и Пола Халмоша] общая философия в отношении линейной алгебры такова: мы думаем в безбазисных терминах, пишем в безбазисных терминах, но когда доходит до серьезного дела, мы запираемся в офисе и вовсю считаем с помощью матриц».
Ирвинг Капланский
Для многих начинающих исследователей данных линейная алгебра становится камнем преткновения на пути к достижению мастерства в выбранной ими профессии.

В этой статье я попытался собрать основы линейной алгебры, необходимые в повседневной работе специалистам по машинному обучению и анализу данных.
Произведения векторов
Для двух векторов x, y ∈ ℝⁿ их скалярным или внутренним произведением xᵀy
называется следующее вещественное число:

Как можно видеть, скалярное произведение является особым частным случаем произведения матриц. Также заметим, что всегда справедливо тождество
.
Для двух векторов x ∈ ℝᵐ, y ∈ ℝⁿ (не обязательно одной размерности) также можно определить внешнее произведение xyᵀ ∈ ℝᵐˣⁿ. Это матрица, значения элементов которой определяются следующим образом: (xyᵀ)ᵢⱼ = xᵢyⱼ, то есть

След
Следом квадратной матрицы A ∈ ℝⁿˣⁿ, обозначаемым tr(A) (или просто trA), называют сумму элементов на ее главной диагонали:

След обладает следующими свойствами:
Для любой матрицы A ∈ ℝⁿˣⁿ: trA = trAᵀ.
Для любых матриц A,B ∈ ℝⁿˣⁿ: tr(A + B) = trA + trB.
Для любой матрицы A ∈ ℝⁿˣⁿ и любого числа t ∈ ℝ: tr(tA) = t trA.
Для любых матриц A,B, таких, что их произведение AB является квадратной матрицей: trAB = trBA.
Для любых матриц A,B,C, таких, что их произведение ABC является квадратной матрицей: trABC = trBCA = trCAB (и так далее — данное свойство справедливо для любого числа матриц).

Нормы
Норму ∥x∥ вектора x можно неформально определить как меру «длины» вектора. Например, часто используется евклидова норма, или норма l₂:

Заметим, что ‖x‖₂²=xᵀx.
Более формальное определение таково: нормой называется любая функция f : ℝn → ℝ, удовлетворяющая четырем условиям:
Для всех векторов x ∈ ℝⁿ: f(x) ≥ 0 (неотрицательность).
f(x) = 0 тогда и только тогда, когда x = 0 (положительная определенность).
Для любых вектора x ∈ ℝⁿ и числа t ∈ ℝ: f(tx) = |t|f(x) (однородность).
Для любых векторов x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) (неравенство треугольника)
Другими примерами норм являются норма l₁
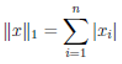
и норма l∞

Все три представленные выше нормы являются примерами норм семейства lp, параметризуемых вещественным числом p ≥ 1 и определяемых как

Нормы также могут быть определены для матриц, например норма Фробениуса:

Линейная независимость и ранг
Множество векторов {x₁, x₂, ..., xₙ} ⊂ ℝₘ называют линейно независимым, если никакой из этих векторов не может быть представлен в виде линейной комбинации других векторов этого множества. Если же такое представление какого-либо из векторов множества возможно, эти векторы называют линейно зависимыми. То есть, если выполняется равенство

для некоторых скалярных значений α₁,…, αₙ-₁ ∈ ℝ, то мы говорим, что векторы x₁, ..., xₙ линейно зависимы; в противном случае они линейно независимы. Например, векторы

линейно зависимы, так как x₃ = −2xₙ + x₂.
Столбцовым рангом матрицы A ∈ ℝᵐˣⁿ называют число элементов в максимальном подмножестве ее столбцов, являющемся линейно независимым. Упрощая, говорят, что столбцовый ранг — это число линейно независимых столбцов A. Аналогично строчным рангом матрицы является число ее строк, составляющих максимальное линейно независимое множество.
Оказывается (здесь мы не будем это доказывать), что для любой матрицы A ∈ ℝᵐˣⁿ столбцовый ранг равен строчному, поэтому оба этих числа называют просто рангом A и обозначают rank(A) или rk(A); встречаются также обозначения rang(A), rg(A) и просто r(A). Вот некоторые основные свойства ранга:
Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). Если rank(A) = min(m,n), то A называют матрицей полного ранга.
Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).
Для любых матриц A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).
Для любых матриц A,B ∈ ℝᵐˣⁿ: rank(A + B) ≤ rank(A) + rank(B).
Ортогональные матрицы
Два вектора x, y ∈ ℝⁿ называются ортогональными, если xᵀy = 0. Вектор x ∈ ℝⁿ называется нормированным, если ||x||₂ = 1. Квадратная м
атрица U ∈ ℝⁿˣⁿ называется ортогональной, если все ее столбцы ортогональны друг другу и нормированы (в этом случае столбцы называют ортонормированными). Заметим, что понятие ортогональности имеет разный смысл для векторов и матриц.
Непосредственно из определений ортогональности и нормированности следует, что

Другими словами, результатом транспонирования ортогональной матрицы является матрица, обратная исходной. Заметим, что если U не является квадратной матрицей (U ∈ ℝᵐˣⁿ, n < m), но ее столбцы являются ортонормированными, то UᵀU = I, но UUᵀ ≠ I. Поэтому, говоря об ортогональных матрицах, мы будем по умолчанию подразумевать квадратные матрицы.
Еще одно удобное свойство ортогональных матриц состоит в том, что умножение вектора на ортогональную матрицу не меняет его евклидову норму, то есть

для любых вектора x ∈ ℝⁿ и ортогональной матрицы U ∈ ℝⁿˣⁿ.

Область значений и нуль-пространство матрицы
Линейной оболочкой множества векторов {x₁, x₂, ..., xₙ} является множество всех векторов, которые могут быть представлены в виде линейной комбинации векторов {x₁, ..., xₙ}, то есть

Областью значений R(A) (или пространством столбцов) матрицы A ∈ ℝᵐˣⁿ называется линейная оболочка ее столбцов. Другими словами,

Нуль-пространством, или ядром матрицы A ∈ ℝᵐˣⁿ (обозначаемым N(A) или ker A), называют множество всех векторов, которые при умножении на A обращаются в нуль, то есть

Квадратичные формы и положительно полуопределенные матрицы
Для квадратной матрицы A ∈ ℝⁿˣⁿ и вектора x ∈ ℝⁿ квадратичной формой называется скалярное значение xᵀ Ax. Распишем это выражение подробно:

Заметим, что

Симметричная матрица A ∈ ????ⁿ называется положительно определенной, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx > 0. Обычно это обозначается как

(или просто A > 0), а множество всех положительно определенных матриц часто обозначают
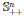
.
Симметричная матрица A ∈ ????ⁿ называется положительно полуопределенной, если для всех векторов справедливо неравенство xᵀ Ax ≥ 0. Это записывается как
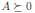
(или просто A ≥ 0), а множество всех положительно полуопределенных матриц часто обозначают

.
Аналогично симметричная матрица A ∈ ????ⁿ называется отрицательно определенной

, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx < 0.
Далее, симметричная матрица A ∈ ????ⁿ называется отрицательно полуопределенной (
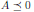
), если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx ≤ 0.
Наконец, симметричная матрица A ∈ ????ⁿ называется неопределенной, если она не является ни положительно полуопределенной, ни отрицательно полуопределенной, то есть если существуют векторы x₁, x₂ ∈ ℝⁿ такие, что

и

.
Собственные значения и собственные векторы
Для квадратной матрицы A ∈ ℝⁿˣⁿ комплексное значение λ ∈ ℂ и вектор x ∈ ℂⁿ будут соответственно являться собственным значением и собственным вектором, если выполняется равенство

На интуитивном уровне это определение означает, что при умножении на матрицу A вектор x сохраняет направление, но масштабируется с коэффициентом λ. Заметим, что для любого собственного вектора x ∈ ℂⁿ и скалярного значения с ∈ ℂ справедливо равенство A(cx) = cAx = cλx = λ(cx). Таким образом, cx тоже является собственным вектором. Поэтому, говоря о собственном векторе, соответствующем собственному значению λ, мы обычно имеем в виду нормализованный вектор с длиной 1 (при таком определении все равно сохраняется некоторая неоднозначность, так как собственными векторами будут как x, так и –x, но тут уж ничего не поделаешь).
Перевод статьи был подготовлен в преддверии старта курса "Математика для Data Science". Также приглашаем всех желающих посетить бесплатный демоурок, в рамках которого рассмотрим понятие линейного пространства на примерах, поговорим о линейных отображениях, их роли в анализе данных и порешаем задачи.
ЗАПИСАТЬСЯ НА ДЕМОУРОК





