В сентябре 2023 года инженеры из гугла выпустили статью об использовании LLM для различных задач оптимизации. Там нет кода или ссылки на репозиторий, чтобы можно было самому поиграть, поэтому я написал простой оптимизатор с помощью языковой модели (Mistral-7B-Instruct) для задачи линейной регрессии.
Коротко о линейной регрессии
Линейная регрессия — это модель зависимости одной переменной от другой (или нескольких) с линейной функцией зависимости. Она позволяет предсказывать значение одной переменной на основании другой или нескольких.
Решить задачу линейной регрессии с одной переменной - значит нарисовать линию, которая будет максимально точно соответствовать существующим наблюдениям. Линия - это уравнение, подставив в которое значение X, мы получим предсказанное значение Y:
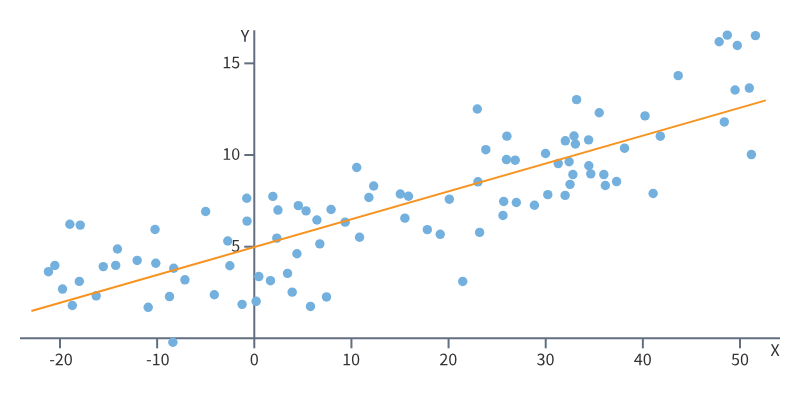
Чтобы оценить, насколько хорошо наша линия подходит под имеющиеся наблюдения, используют различные методы. Самый известный - метод наименьших квадратов (МНК). С его помощью мы определяем насколько далеко реальные наблюдения отдалены от нашей линии. Задача - минимизировать эти расстояния.
Функцию, которая рассчитывает расстояния, называют функцией потерь (loss function или cost function). И мы хотим её минимизировать.
Задача линейной регрессии имеет аналитическое решение. Когда с помощью манипуляций с производными мы получаем явную формулу и находим точное решение (правильную линию). Но если переменных и наблюдений слишком много, то аналитическое решение может быть вычислительно-затратным или даже невозможным.
Тогда на помощь приходят итерационные методы. Самый известный - градиентный спуск.
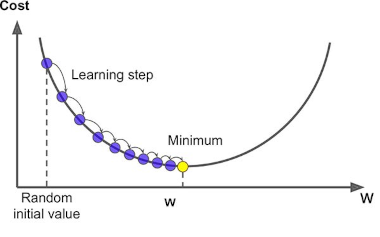
Во время градиентного спуска мы как бы проверяем: если я немного увеличу значение переменной w, то будет ли моя линия лучше подходить под имеющиеся наблюдения? Если да, то я немного увеличиваю w, если нет - уменьшаю. И так двигаюсь до тех пор, пока не окажусь в оптимальном минимуме.
Думаю, что-то похожее будет делать наша языковая модель, когда будет подбирать идеальные коэффициенты на основании только текстовых инструкций.
Больше про линейную регрессию - тут.
Про градиентный спуск - тут.
Функцию потерь - тут.
Оптимизируем с помощью LLM
Пайплайн:
Создадим набор данных со значениями y, x;
Случайно инициируем веса (w, b) для нашей линии y_pred = w*x + b;
Передадим модели инструкцию, в которой скажем, какое значение принимает наша функция потерь при заданных w, b. И попросим её изменить w, b таким образом, чтобы уменьшить функцию потерь. (Модель не будет знать, какую функцию мы оптимизируем. Мы будем подавать ей только значения: w, b, loss);
Возьмём предложенные моделью w, b, посчитаем для них loss и снова подадим модели. (Сначала на входе у модели будет всего один пример - случайно инициированные веса, а затем к нему буду добавляться примеры, которые она сама придумала, но не больше 10 штук);
Дождёмся, когда 3 последних значения loss функции станут меньше 1 и примем это за оптимальное решение.
Загружаем модель Mistral-7B-Instruct-v0.1 с Hugging Face:
import torch
from transformers import AutoModelForCausalLM, AutoTokenizer
device = "cuda"
model = AutoModelForCausalLM.from_pretrained("mistralai/Mistral-7B-Instruct-v0.1",
device_map=device,
torch_dtype=torch.bfloat16)
tokenizer = AutoTokenizer.from_pretrained("mistralai/Mistral-7B-Instruct-v0.1")Создадим набор данных:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
x = np.arange(0, 6, 0.5) # создаём истинные значения для x
y = 3*x + np.random.randint(-1, 2, 12) # создаём истинные значения для y + шум
# инициируем случайные веса для нашей линии y_pred = w*x + b
# во время оптимизации мы будем менять веса w, b, рассчитывать y_pred
# и сравнивать их с истинными значениями "y", определёнными выше
w = np.random.uniform(-5, 5)
b = np.random.uniform(-5, 5)Построим график:
fig, ax = plt.subplots()
ax.scatter(x, y)
ax.plot(x, w*x + b, c='red')
ax.set_xlabel('x')
ax.set_ylabel('y');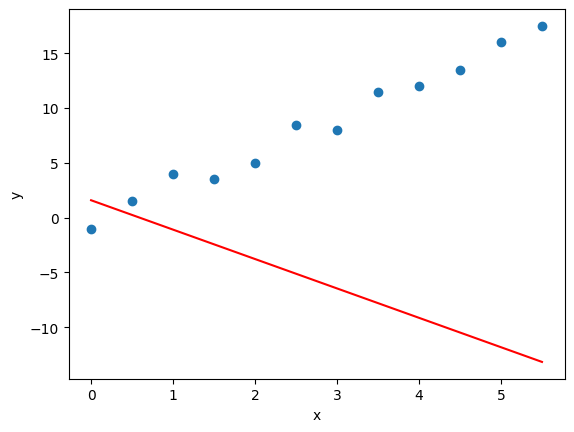
Красная линия - наш ответ со случайно инициированными весами (w, b).
Выглядит не очень.
Напишем несколько функций для парсинга ответов LLM, расчёта loss:
def is_number_isdigit(s): # парсинг str ответа от LLM
n1 = s[0].replace('.','',1).replace('-','',1).strip().isdigit()
n2 = s[1].replace('.','',1).replace('-','',1).strip().isdigit()
return n1 * n2
# останавливаем оптимизацию, когда последние "last_nums" значений loss < 1
def check_last_solutions(loss_list, last_nums):
if len(loss_list) >= last_nums:
last = loss_list[-last_nums:]
return all(num < 1 for num in last)
def loss_calc(y, w, x, b):
return ((y - w*x + b)**2).mean() # функция потерь МНК
loss = loss_calc(y, w, x, b) # рассчитаем первый loss для случайных (w, b)
d = {'loss': [loss], 'w': [w], 'b': [b]}
loss_list = [loss] # соберём все loss для построения графика в конце
df = pd.DataFrame(data=d) # датасет c предложеными моделью весами (w, b) и loss
df.sort_values(by=['loss'], ascending=False, inplace=True)Посмотрим loss со случайно инициированными w, b:
dfOutput:
loss w b
404.096928 -2.683655 1.586905Создаём промт:
# num_sol - максимальное кол-во наблюдений в промте
def create_prompt_bias(num_sol):
meta_prompt_start = f'''Now you will help me minimize a function with two input variables w, b. I have some (w, b) pairs and the function values at those points.
The pairs are arranged in descending order based on their function values, where lower values are better.\n\n'''
solutions = ''
if num_sol > len(df.loss):
num_sol = len(df.loss)
for i in range(num_sol):
solutions += f'''input:\nw={df.w.iloc[-num_sol + i]:.3f}, b={df.b.iloc[-num_sol + i]:.3f}\nvalue:\n{df.loss.iloc[-num_sol + i]:.3f}\n\n'''
meta_prompt_end = f'''Give me a new (w, b) pair that is different from all pairs above, and has a function value lower than
any of the above. Do not write code. The output must end with a pair [w, b], where w and b are numerical values.
w, b ='''
return meta_prompt_start + solutions + meta_prompt_end# Вот так будет выглядеть промт для двух решений.
# Значения сотрируются по loss(value) по убыванию.
Now you will help me minimize a function with two input variables w, b. I have some (w, b) pairs and the function values at those points.
The pairs are arranged in descending order based on their function values, where lower values are better.
input:
w=-0.456, b=0.357
value:
135.314
input:
w=0.700, b=0.450
value:
63.494
Give me a new (w, b) pair that is different from all pairs above, and has a function value lower than
any of the above. Do not write code. The output must end with a pair [w, b], where w and b are numerical values.
w, b =Запускаем цикл оптимизации:
num_solutions = 10 # кол-во наблюдений, которое будем подавать в промт
for i in range(500):
text = create_prompt(num_solutions)
model_inputs = tokenizer([text], return_tensors="pt").to(device)
model.to(device)
generated_ids = model.generate(
**model_inputs,
max_new_tokens=15,
temperature=0.8,
do_sample=True,
pad_token_id=50256
)
output = tokenizer.batch_decode(generated_ids)[0]
response = output.split("w, b =")[1].strip()
if "\n" in response:
response = response.split("\n")[0].strip()
if "," in response:
numbers = response.split(',')
if is_number_isdigit(numbers):
w, b = float(numbers[0].strip()), float(numbers[1].strip())
loss = loss_calc(y, w, x, b)
loss_list.append(loss)
new_row = {'loss': loss, 'w': w, 'b': b}
new_row_df = pd.DataFrame(new_row, index=[0])
df = pd.concat([df, new_row_df], ignore_index=True)
df.sort_values(by='loss', ascending=False, inplace=True)
if i % 20 == 0: # принтуем каждый 20-ый шаг
print(f'{w=} {b=} loss={loss:.3f}')
if check_last_solutions(loss_list, 3):
breakOutput:
w=-100.0 b=1.0 loss=112593.792
w=-1.5 b=0.9 loss=245.704
w=2.2 b=1.1 loss=15.197
w=-2.0 b=-1.0 loss=246.792
w=3.5 b=1.2 loss=0.809Посмотрим последние 10 значений loss:
print(*loss_list[-10:], sep='\n')44.41708333333333
28.161666666666665
26.42833333333333
21.763333333333335
46.583333333333336
20.939537499999997
20.939537499999997
0.80875
0.80875
0.6437500000000002А вот так теперь выглядит наша прямая:
fig, ax = plt.subplots()
ax.scatter(x, y)
ax.plot(x, w*x + b, c='red');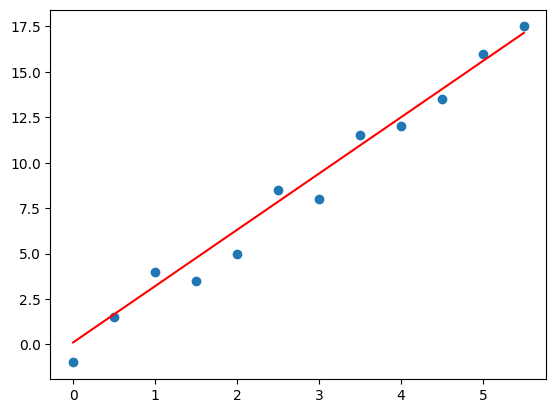
Посмотрим на снижение loos во время оптимизации (ограничил значения 700 единицами, потому что в процессе тренировки было несколько выбросов со значениями больше миллиона).
fig, ax = plt.subplots()
print(f'number of step = {len(loss_list)}')
ax.plot([x for x in loss_list if x < 700]);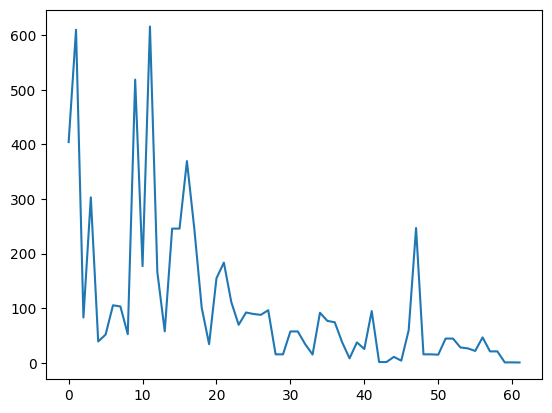
Интересное наблюдение. Температура (temperature), параметр, который отвечает за вариативность ответов модели, играет в нашем случае своеобразную роль шага для градиентного спуска. Чем ниже температура, тем медленнее снижается loss, но в то же время реже встречаются выбросы. И наоборот - чем выше температура, тем более уверенные "шаги" делает модель, быстрее сходится, но и часто отдаёт большие выбросы.
Вот так, например, выглядит снижение loss при temperature=0.5 через каждые 20 итераций:
w=-0.001 b=2.73 loss=153.029
w=0.0 b=2.73 loss=152.950
w=1.0 b=2.73 loss=83.893
w=0.333 b=1.73 loss=108.150
w=0.5 b=1.73 loss=97.242
w=0.94 b=1.73 loss=71.318
w=0.97 b=1.75 loss=69.999
w=0.995 b=1.715 loss=68.143
w=0.999 b=1.719 loss=67.990
w=0.999 b=1.719 loss=67.990
w=0.999 b=1.719 loss=67.990
w=0.999 b=1.719 loss=67.990
w=0.719 b=0.2 loss=61.172
w=0.75 b=0.15 loss=58.963
w=0.852 b=0.1 loss=53.394
w=0.905 b=0.095 loss=50.863
w=0.918 b=0.078 loss=50.063
w=0.922 b=0.068 loss=49.762
w=0.931 b=0.063 loss=49.294
w=0.936 b=0.056 loss=48.985
w=0.935 b=0.057 loss=49.042
w=0.939 b=0.054 loss=48.826
w=0.939 b=0.054 loss=48.826
w=0.946 b=0.051 loss=48.475
w=0.934 b=0.043 loss=48.922P. S.
Не стоит рассматривать языковую модель, как реальный инструмент для оптимизации в таких задачах. Для решения задачи линейно регрессии существуют куда более простые, быстрые и менее затратные методы (для запуска Mistral-7B-Instruct в формате bfloat16 требуется видеокарта с памятью как минимум 16Gb).
Но в целом тенденция выглядит немного пугающей. Даже относительно небольшие LLM становятся всё более "умными", а люди находят им всё новые применения. Например, в статье, на которую я ссылался вначале, авторы предлагают метод оптимизации промтов - а это уже реальная заявка на то, чтобы отобрать работу у промт инженеров (ну или по крайней мере внести существенные коррективы в их обучение).
Репозиторий с кодом на GitHub - https://github.com/akocherovskiy/LLM_as_optimizer
Google Colab, где можно запустить код на бесплатной Т4 - LLM_as_optimizer





