Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
Настоящая статья продолжает тему предыдущей работы (https://habr.com/ru/post/560266/) и также посвящается особо замудренным способам заполнения двухмерных массивов согласно определенному шаблону. Создание громоздких, неуклюжих формул, без применения таких милых сердцу программиста конструкций как циклы и условия оказалось увлекательным занятием. В связи с этим, автор, уподобляясь некоторым государственным чинам (вспоминаем бородатую шутку про разницу между депутатом и программистом), решил потратить кучу драгоценного времени на очередной интересный, но, увы, бесполезный в практическом плане проект. Речь идет о вычислении математическим путем элементов массивов, заполняемых змееподобной траекторией, или проще говоря – «тещиных» матриц.
Различают два класса этих самых матриц: обычные (злобные) и диагональные (крайне злобные).
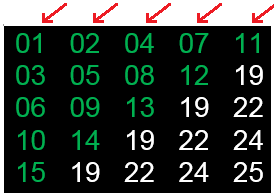
Первый класс двухмерных массивов (здесь и далее речь идет только о квадратных матрицах) заполняется натуральными числами от 1 до N2 с левого верхнего угла построчно:

При этом, с учетом наличия у квадрата 4-х сторон, а у каждой стороны - 2-х углов, в данном классе содержится еще 7 видов, если подойти к этому вопросу основательно.
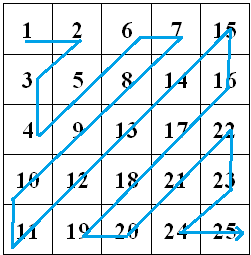
Второй класс тещиных матриц заполняется значениями от 1 до N2 с левого верхнего угла по диагоналям, и аналогично предыдущему, может иметь еще 7 видов (начинаться с любого из четырех углов в двух направлениях). Однако, мы в качестве примеров будем рассматривать только наиболее удобные варианты, традиционно начинающиеся с левого верхнего угла.
Итак, постараемся предельно четко сформулировать задачу: вывести математически «чистые» формулы вычисления значений элементов вышеуказанных матриц на основании их координат (I, J) и размерности (N). При этом, не допускается использовать условные переходы и заранее заготовленные наборы данных: массивы, словари, множества и т.д. Циклы используются только для перебора всех элементов матрицы и также не применяются непосредственно в вычислениях.
Подготовка. Математический аппарат будет строиться параллельно с разработкой кода на языке С++. Для обеспечения программной реализации решений подготовим соответствующий скрипт, объявив в нем массив размером 5x5 (присвоим ему оригинальное наименование «a») и заполнив его нулевыми значениями. Формулы будут строиться и проверяться поэтапно в процессе их одновременной работы со всеми элементами матрицы, перебор которых производится традиционным способом двумя вложенными циклами от 1 до N.
Работа состоит из двух частей. В первой части выводим формулу для матриц, заполненных в горизонтальном порядке, а во второй – для матриц, заполненных в диагональном порядке.
Основной скрипт для обеих частей выглядит следующим образом:
#include <iostream>
using namespace std;
int main()
{
int N = 5; // задаем размер матрицы
int a[N][N]; // и инициализируем ее
for (int ik = 0; ik < N; ik++)
for (int jk = 0; jk < N; jk++)
a[ik][jk] = 0; // заполнив для удобства нулями
for (int ik = 0; ik < N; ik++){ //назовем его "Основной цикл"
for (int jk = 0; jk < N; jk++){
int i = ik + 1; // Номера строк и столбцов приводим в удобный
int j = jk + 1; // в математическом плане вид (от 1 до N)
// ... здесь будем вставлять основной код вычислений
}
}
for (int ik = 0; ik < N; ik++){ //Блок "Вывод массива"
for (int jk = 0; jk < N; jk++){
printf( " %02d " , a[ik][jk]);// дополняем число ведущими нулями
}
cout << endl;
}
return 0;
}1 класс матриц (в построчном исполнении)
В построчном виде достаточно легко вывести соответствующую формулу и применить ее для заполнения массива. В данной статье это решение приводится только в качестве небольшой разминки.
Итак, анализ расстановки элементов матрицы показывает (см. Рисунок 1), что наибольшими компонентами непрерывного изменения значений (цельные отрезки, где значения изменяются на +1 или -1) являются строки. Таким образом, номер строки будет играть ведущую роль, а номер столбца обеспечивать прирост/убывание значений элементов.
Для начала выведем число согласно порядковому номеру ячейки, который возрастает в привычном для нас направлении «слева-направо» и «сверху-вниз».

Вводим соответствующий код в компиляторе:
…
a[ik][jk] = (i - 1) * N + j;
…И получаем выходные данные:

Как видим, от желаемого результата нас разделяют лишь четные строки, в которых прирост должен быть в обратном порядке.
Следовательно, выведем формулу для заполнения элементов в обратном порядке.
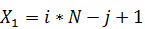
Введем соответствующий код в компиляторе:
…
a[ik][jk] = i * N + 1 + j;
…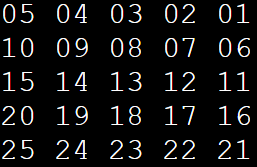
Полагается, с учетом целевой аудитории, что детальных пояснений для этих простейших решений не требуется. На текущий момент важно, что мы имеем две разные формулы, которые необходимо объединить в одном уравнении, обеспечив их поочередную работу, в зависимости от четности/нечетности строки.
Для этого используем кусочно-заданную функцию, складывая оба значения X, предварительно умножив каждый из них на остаток от целочисленного деления номера строки на 2. В случае X1 это (i mod 2), а в случае X2 это (i + 1) mod 2.
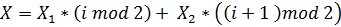
Подставляем вместо X1 и X2 полные значения:
Переводим все это на С++ и наблюдаем конечный результат:
…
a[ik][jk] = ((i - 1) * N + j) * (i % 2) + (i * N + 1 - j) * ((i + 1) % 2);
…
2 класс матриц (в диагональном исполнении)
В диагональном исполнении задача является на порядок сложнее, требует значительно большего времени, а также разделения ее на несколько этапов. Однако, прежде чем приступить к штурму крепости, приведем некоторые, необходимые в дальнейшем, определения:
Главная диагональ - диагональ, проведённая из левого верхнего угла матрицы в правый нижний.
Побочная диагональ - диагональ, проведённая из левого нижнего угла матрицы в правый верхний (Рисунок 6).

В данной задаче участками непрерывного изменения значений являются побочная и параллельные ей диагонали. Для удобства в будущем диагонали также будем именовать «блоками», а побочную диагональ «центральной» (не путать с «главной»).
1 этап. Итак, приступим. Общее количество блоков равно 2 * N – 1, где N – размер матрицы. В нашем случае при размерах матрицы 5*5 это будет 9. Далее, для наглядности выделим и пронумеруем эти диагонали (Рисунок 7).
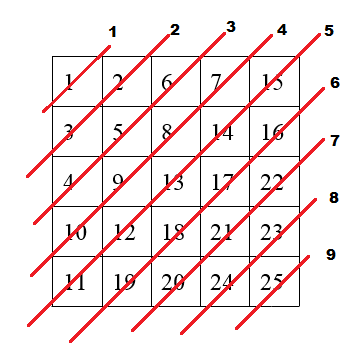
Следующим шагом приводим матрицу с адресами ее элементов, для удобного изучения их связи с желаемыми значениями (Рисунок 8).

В данном случае явно наблюдаем зависимость порядкового номера диагонали от суммы номера строки и столбца. Т.е. D = i + j – 1.
Кроме того, количество элементов начиная с первой до центральной диагонали увеличивается на 1, а после нее уменьшается на такое же значение. Сей очевидный даже для школьника факт необходимо было здесь отметить, так как он указывает на фиксированность количества элементов в каждом блоке и, соответственно, диапазона значений. Это также позволяет вывести ту часть формулы, которая по номеру строки и номеру столбца определит максимальное число в каждом блоке.
Так, если в первой диагонали 1 элемент, во второй 2, в третьей 3, то у нас на лицо арифметическая прогрессия с разностью d = 1 и начальным значением a1 = 1.
В свою очередь, искомые значения элементов, представлены в следующих диапазонах: в блоке 1 – [1], в блоке 2 – [2..3], в блоке 3 – [4..6] и так далее до центральной диагонали включительно.
Вычислить максимальное число в каждой диагонали возможно с помощью формулы суммы арифметической прогрессии:

(Касательно знаков деления: с учетом особенностей текстового редактора Хабра, дробные выражения используются в отдельно стоящих формулах, а знак «/» в математических выражениях встречающихся непосредственно в тексте. Оба этих знака являются эквивалентами и означают деление в широком смысле, которое, однако, в настоящей работе всегда предполагает целочисленные результаты. В отдельных местах, где важно подчеркнуть именно операцию целочисленного деления используется знак «÷». Получение остатка от целочисленного деления обозначается «mod». Прим автора.)
Поскольку в нашем случае a1 = 1 и d = 1, то формула немного упрощается, и ее единственным аргументом остается n – порядковый номер члена прогрессии:

Таким образом, мы можем определить верхний предел значений (максимальное число) в каждой конкретной диагонали.
К примеру, в четвертой диагонали максимальное значение S4 = (4 + 42) / 2 = 10, в чем можно убедиться, взглянув на Рисунок 6. Однако данный подход будет работать только до центральной диагонали, поскольку после нее количество элементов в блоках начинает уменьшаться на единицу (отрицательный рост :)). В целом, все дальнейшие вычисления предполагают отдельный подход к значениям до и после побочной диагонали. Поэтому, для удобства, первую часть матрицы (все диагонали до центральной включительно) условно назовем сектором «А», а вторую сектором «В» (остальные элементы). Эти буквы также будут фигурировать в названиях некоторых переменных, в зависимости от их роли, как в математических формулах, так и непосредственно в коде программы.
Теперь представим окончательное выражение, предварительно обозначив номер диагонали переменной D (вместо «n» из общей математической формулы), а максимальное значение – Ma (вместо Sn):
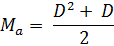
Пишем эти вычисления на языке С++ и наблюдаем результат (Рисунок 9):
…
int D = i + j - 1;
int Ma = (D * D + D) / 2;
a[ik][jk] = Ma;
… 
Как и отмечалось выше, в секторе «А» появились необходимые значения. Вместе с тем, числа после центральной диагонали явным образом не соответствуют ожиданиям. Причиной этому является неспособность одновременного использования формулой прироста в секторе «А» (d = 1) и уменьшения в секторе «В» (d = -1). К примеру, в 6-ой диагонали она видит 6 элементов (в 7-ой 7 и т.д.), а реализация формулы в программном коде демонстрирует нам только 4 элемента со значением 21.
Теперь попытаемся решить эту проблему. Так, дальнейшие вычисления в условиях отрицательного роста возможно производить применяя ту же формулу суммы арифметической прогрессии, но с другими исходными данными.
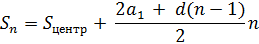
Здесь:
d = -1, убывание
n – порядковый номер члена прогрессии, а в нашем случае номер диагонали в секторе «В» относительно его начала, т.е. D – N,
a1 - длина первой диагонали в секторе «В», т.е. N - 1,
Sцентр – максимальное значение элементов в центральной диагонали, т.е. (N2 + N) / 2.
Далее введем переменную Mb, которая будет содержать максимальные значения для диагоналей сектора «В» и заменим ей Sn.
В результате получаем следующее выражение:
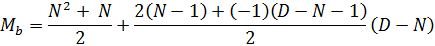
Раскрывая скобки, умножая, сокращая и совершая прочие математические извращения, выводим более компактную формулу:

Кодируем ее и анализируем результаты:
…
int Mb = (N * N + N) / 2 + ((3 * N – D - 1) * (D - N)) / 2;
a[ik][jk] = Mb;
…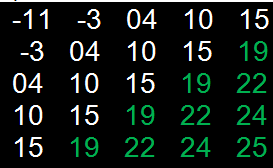
Как видим, сектор «В» в этот раз состоит из необходимых чисел, но в секторе «А» большинство элементов содержат неправильные значения. Проблема также решается с помощью кусочно-заданной функции.
В результате этих манипуляций мы имеем две формулы, одна из которых работает корректно до центральной диагонали:

а вторая после:

Эти два выражения следует объединить в одной функции, с условием, чтобы каждое из них работало корректно в своем секторе. Приблизительно таким образом:
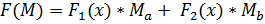
Здесь функция F1(x) принимает значение 1 в секторе «А» и 0 в секторе «В», а F2(x) наоборот. Получается некое подобие битовой маски.
Для реализации этого замысла применим целочисленное деление и разделим номер диагонали на порядок матрицы увеличенный на одну единицу:

Набираем в компиляторе и смотрим результат:
…
a[ik][jk] = D / (N + 1);
…
Как видим сектор «А» в данном случае равняется нулю, а сектор «В» - 1. Эти результаты будем помещать в переменную Cb. Для того чтобы получить диаметрально противоположенные значения, достаточно инвертировать результаты следующим выражением:

Теперь введем новую переменную Ca, поместим в нее результат работы последней формулы и внесем соответствующий код в скрипт:
…
int Ca = abs (D / (N + 1) - 1);
a[ik][jk] = Ca;
…
Таким образом, на текущий момент мы вооружились всеми необходимыми элементами для вычисления максимальных значений в диагоналях.
Остается собрать все отдельные компоненты в единое математическое выражение
M = Ma * Ca + Mb * Cb, и соответственно написать в С++ полный код по предыдущим действиям.
…
int D = i + j - 1;
int Ma = (D * D + D) / 2;
int Mb = (N * N + N) / 2 + ((3 * N - D - 1) * (D - N)) / 2;
int Ca = abs (D / (N + 1) - 1);
int Cb = D / (N + 1);
a[ik][jk] = Ca * Ma + Cb * Mb;
…
Как видим, этот этап завершен, во всех диагоналях находятся требуемые максимальные значения.
2 этап. Теперь необходимо завершить работу, превратив одинаковые значения в возрастающую группу чисел соответствующего диапазона в каждом блоке. Этого можно достичь вычитая из элементов определенные значения. Снова взглянем на матрицу с индексами.

В секторе «А», индексы элементов в каждом блоке находятся в диапазоне от 1 до длины блока (которая эквивалентна номеру диагонали). Соответственно, вычитая из максимальных значений i или j увеличенный на 1, мы можем получить нужные числа. Однако, результирующие значения будут расположены в возрастающем порядке только с начала (сверху-вниз), либо только с конца блока (снизу-вверх).
При использовании j в качестве вычитаемого, направление прироста будет сверху-вниз:

Следует отметить, что пока мы не будем затрагивать сектор «В».
Кодируем последнее выражение и любуемся результатом:
…
a[ik][jk] = Ca * (Ma - j + 1) + Mb * Cb;
…
Отсюда можно сделать логический вывод, что заменив i на j, мы получим обратный результат в виде прироста снизу-вверх. Окончательный же вид змеевидной матрицы сформируется путем чередования направлений прироста «сверху-вниз» и «снизу-вверх».
Добиваться этого следует использованием еще одного элемента кусочно-заданной функции, который будет принимать значение 0 или 1 в зависимости от четности или нечетности номера диагонали.
Для этого введем две переменные: Co (odd numbers) для нечетных блоков и Ce (even numbers) для четных. Co вычислим выражением D mod 2 (при нечетном D он будет равняться 1, при четном 0) и Ce - (D + 1) mod 2 (соответственно наоборот). Вставляем эти элементы в
формулу так, чтобы вычитание j происходило в четных диагоналях, а вычитание i в – нечетных:

Кодируем это и восхищаемся результатом:
…
int Co = D % 2;
int Ce = (D + 1) % 2;
a[ik][jk] = Ca *((Ma - j + 1)* Ce + (Ma - i + 1) * Co) + Cb * (Mb);
…
Получается вот такая картина, то есть половина тещи змеи у нас уже готова.
Приведение в норму сектора «В» происходит похожим способом. Однако здесь простое вычитание номера строки или столбца не приведет к корректным результатам, так как i и j находятся в диапазоне 2..N. Для получения правильных значений в качестве вычитаемого используем разницу «N – i» или «N – j». В первом случае у нас направление прироста будет сверху-вниз, а во втором - наоборот.
Расширим нашу предыдущую формулу:

и реализуем ее в программном виде:
…
a[ik][jk] = Ca *((Ma - j + 1)* Ce + (Ma - i + 1) * Co) + Cb * (Mb - (N - i));
…
Рисунок 17 демонстрирует, что осталось только скорректировать направления прироста по аналогии с сектором «А», в зависимости от четности номера диагонали используя уже готовые переменные Ce и Co:

Кодируем и, в этот раз - по-взрослому, восхищаемся результатами:
…
a[ik][jk] = Ca *((Ma - j + 1)* Ce + (Ma - i + 1) * Co)
+ Cb * ((Mb - (N - i)) * Ce + (Mb - (N - j)) * Co);
…
В завершении следует собрать все формулы и выражения, а также программный код в одном месте, чтобы у читателя возникло целостное представление о проделанное работе.
Математика:

Код на С++:
…
int D = i + j - 1;
int Ma = (D * D + D) / 2;
int Mb = (N * N + N) / 2 + ((3 * N - D - 1) * (D - N)) / 2;
int Ca = abs (D / (N + 1) - 1);
int Cb = D / (N + 1);
int Co = D % 2;
int Ce = (D + 1) % 2;
a[ik][jk] = Ca *((Ma - j + 1)* Ce + (Ma - i + 1) * Co)
+ Cb * ((Mb - (N - i)) * Ce + (Mb - (N - j)) * Co);
…3 этап. Сокращение. На предыдущем этапе мы вывели более или менее обоснованную формулу вычисления значений элементов, разъяснили каждый шаг. В то же время, не попытаться ее сократить, было бы проявлением неуважения к математике и всем знаменитым деятелям, которые развили эту науку до сегодняшнего состояния.
Итак, вернемся к моменту вычисления максимальных значений в секторе «В»:

раскроем здесь скобки,
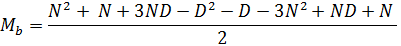
и сократим
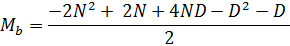
Наше уравнение стало немного короче, хоть и не на столько, чтобы это имело существенное значение. Однако, если присмотреться можно узреть – D2 – D, часть выражения, которая является в некотором роде антагонистом Ma = (D2 + D) / 2, формулы вычисления максимальных значений в секторе «А». Возможно ли как-нибудь обратить «– D2 – D» из негатива в позитив? Конечно, если его записать в виде «D2 + D – 2D2 – 2D», по сути, увеличив количество негатива в уравнении. Пробуем, предварительно собрав все D-элементы в начале выражения:

Теперь мы можем легко вычленить из общей дроби (D2 + D) / 2, при этом, не забывая инвертировать знаки в оставшейся части (так как мы выводим знак «минус» перед второй дробью):
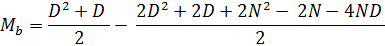
Разделим вторую дробь на 2:
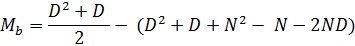
Таким образом, на данный момент формула отдельным членом содержит выражение
(D2 + D) / 2. То есть, мы на пути к тому, чтобы вместо двух уравнений для Ma и Mb использовать одно. Но и это еще не все, так как здесь припасен небольшой бонус. В частности, проанализировав вычитаемое (D2 + D + N2 – N + 2ND), можно увидеть многочлен квадратов суммы разницы (вспоминаем правило (a - b)2 = a2 – 2ab + b2), т.е. D2 – 2ND + N2. Собрав его (многочлен), получаем более компактное уравнение:
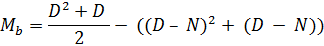
Итак, наша новая формула в целом позволяет вычислить Mb, а также содержит выражение для вычисления Ma. Чтобы заставить ее работать на оба сектора корректно, достаточно умножить «(D – N)2 + (D – N)» на определитель сектора «В» - Cb или D ÷ (N + 1). Теперь запишем окончательный вариант, используя вместо Mb просто M.
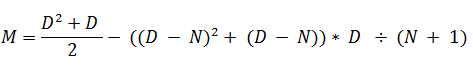
Набираем соответствующую команду в компиляторе и наблюдаем результат:
…
int M = (D * D + D) / 2 - ((D - N) * (D - N) + (D - N)) * (D / (N + 1));
a[ik][jk] = M;
…
Как вы могли убедиться, максимальные значения в каждом блоке возможно получить и более коротким путем. Теперь осталось немногое – вычесть из них номера строк или столбцов, в зависимости от направления прироста.
Возвращаемся к формуле:
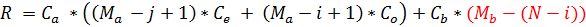
Здесь для коррекции сектора «А» мы вычитали (j – 1), а для коррекции сектора «В» (N – i). Однако в том случае у каждого сектора были независимые вычисления. Теперь же придется прийти к какому-то общему выражению и согласовать «(j – 1)» и «(N - i)». Конечно, мы бы могли снова задействовать определители секторов Ca и Cb, но тогда длина формулы практически вернулась бы в исходное состояние, делая бессмысленными наши потуги ее сократить.
Далее, поработаем отдельно с сектором «В», добавив в него «(N - i)». При этом не забываем, что попадая внутрь скобок, перед которым стоит знак «-», знак непосредственно самого -
«(N - i)» инвертируется. Выделим нужный участок красным, также заменив D на i + j – 1.
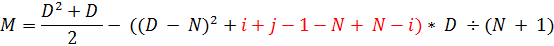
Сокращаем ненужное и получаем:
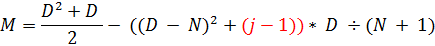
Пробуем в это в компиляторе:
…
int M = (D * D + D) / 2 - ((D - N) * (D - N) + (j - 1))* (D / (N + 1));
a[ik][jk] = M;
…
В результате получаем корректные значения в секторе «В», с приростом «сверху-вниз».
Теперь же, чтобы распространить корректировку на всю матрицу, достаточно вытащить за скобки «j – 1», опять же, не забывая об инвертировании знаков.

Пробуем в С++:
…
a[ik][jk] = (D * D + D) / 2 - ((D - N) * (D - N))* (D / (N + 1)) - j + 1;
…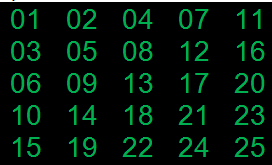
Как видим, у нас получается искомая матрица, с приростом значений в диагоналях сверху-вниз.
Наконец, приступим к последнему шагу – обеспечим чередование направлений. Это сделать очень легко - достаточно задействовать уже имеющиеся определители четности, чередуя вычитание i или j.

Набираем соответствующую команду в С++ и снова восхищаемся результатом:
…
a[ik][jk] = (D * D + D)/2 - ((D - N) * (D - N))* (D / (N + 1)) - j * Ce - i * Co + 1;
…
Опять же, для обеспечения целостности картины соберем все формулы и команды в одном месте, избавившись при этом от определителей четности диагоналей (заменив их полными выражениями).
Математика:
N = размер матрицы.
D = i + j – 1. (D – переменная, номер диагонали).
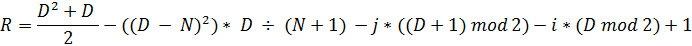
Программный код:
…
int D = i + j - 1;
int R = (D * D + D) / 2 - ((D - N) * (D - N))* (D / (N + 1))
- j * ((D + 1)%2)- i * (D % 2) + 1;
a[ik][jk] = R;
…Итого, нам удалось значительно сократить формулу, а также программный код.
Заключение.
Автор ни в коем случае не претендует на первенство в решении этой задачи приведенным способом, так как из миллионов программистов во всем мире наверняка нашлись бы и другие любители подметать ломом асфальт (или красить траву в зеленый цвет). Таким же образом признается отсутствие какого-либо практического применения полученных результатов. Кроме того, заполнение всей матрицы посредством привычных циклов и условий, вероятно, потребует гораздо меньшего времени, чем путем вычисления каждого элемента громоздким набором арифметических операций (хотя, эту гипотезу еще надо доказать).
Однако, рассматривая вопрос чисто с теоретической точки зрения, возможно отметить преимущество формулы перед традиционным «цикло-условным» решением. Для этого представим ситуацию, в которой не требуется заполнение всего массива, а необходимо вычисление значения только одной ячейки. Массив, в свою очередь, огромен (ну скажем 10000*10000); координаты искомого элемента находятся где-нибудь в середине. В таком случае получить результат одной функцией будет гораздо быстрее, нежели проходить циклом со счетчиком до середины матрицы. Сложно, конечно, в реальности представить такую ситуацию, но на то она и теория.
В данном контексте можно сослаться на неустанно увеличивающиеся вычислительные мощности современных компьютеров, которые в какой-то мере нивелируют потребность в оптимизации алгоритмов и экономии ресурсов. Однако не следует забывать и о соответствующем росте объемов обрабатываемых данных. К тому же, процессоры используются не только в пользовательских компьютерах или даже огромных серверах, установленных в комфортных помещениях (речь идет о комфорте для вычислительной техники). В современном мире вычислительные машины больше и больше применяются за пределами обозначенных мест, где физические условия зачастую бывают экстремальными. Само собой это может ограничивать процессоры в размерах и других параметрах, в конечном счете, ограничивая их вычислительные возможности.
Таким образом, вопрос о решении различных задач кратчайшим и наименее затратным способом остается актуальным.