Можно ли вычислить массу монеты по звуку её падения?

Однажды я случайно задел книжный шкаф и с него упала монета. Это натолкнуло меня на мысль: можно ли вычислить массу монеты на основании звука, который она издала при падении?

Если у нас есть размеры и материал объекта, то можно вычислить и массу, и тип нормального колебания. Одной лишь массы недостаточно — большая бумажная «монета» будет иметь сильно отличающуюся основную частоту от маленького вольфрамового шара.

Связь между основной частотой звяканья монеты и её массой задаётся (приблизительно) уравнением

$$

где

$$ = модуль Юнга

$$ = толщина

$$ = масса монеты

$$ = диаметр монеты

$$ = основная частота

Сейчас я подробно расскажу, как вывел это уравнение…

Если предположить, что все «монеты» имеют одинаковое соотношение размеров (отношение диаметра к толщине) и изготовлены из одинакового материала, то действительно можно вычислить связь между основной частотой и массой. По анализу размерностей, если мы предположим, что частота — функция от

• $$: соотношения размеров (безразмерная величина: изначально предполагается константой, игнорируется)
• $$: диаметра ($$)
• $$: плотности ($$)
• $$: модуля ($$)

Тогда сочетание всего вышеуказанного, дающее нам размерность $$ — это

$$

Скомбинировав это с массой объекта, которая пропорциональна $$, и допустив, что $$ постоянна (чтобы можно было устранить её из уравнения), мы получим

$$

Другими словами, масса снижается с третьей степенью частоты для монет с одинаковым материалом и соотношением размеров.

Но монеты США устроены иначе. На сайте Монетного двора США я нашёл следующую информацию:

                                                Соотношение
монета      масса   диаметр  толщина   материал размерностей
пенни       2,500    19,05     1,52       Zn*      12,53
5 центов    5,000    21,21     1,95      Cu-Ni     10,88
10 центов   2,268    17,91     1,35      Cu-Ni     13,27
25 центов   5,670    24,26     1,75      Cu-Ni     13,86
старый 1 ц. 3.11     19,05     1,52     Бронза.    12,53
* с медным покрытием...

То есть материал, как и соотношение размерностей, не всегда одинаковы. Это немного усложнит доказательство взаимосвязи.

Но давайте всё-таки попробуем. Из экспериментальных данных (информация alemi) я получил следующие основные частоты:

пенни         12,6
5 центов      12,4
10 центов     12,8
25 центов      9,2

Здесь интересны 25 и 10 центов, потому что они состоят из одного материала и имеют самое близкое соотношение размеров (13,3 и 13,9, то есть разница всего 5%). Из соотношения их масс (2,500), можно ожидать, что соотношение частот будет 0,74 ($$). А измеренное соотношение оказалось равным 0,72. На самом деле, очень близко…

Иными словами, если мы знаем частоты 10 и 25 центов, и нам нужно вычислить массу 25 центов по 10 центам, мы получим

$$

что даёт погрешность около 7%, или меньше 0,5 г. Мне кажется, это потрясающе, учитывая разницу масс в 2,5 раза между 25 и 10 центами.

Вдохновлённый этим результатом, я решил посмотреть, можно ли найти общее для всех четырёх монет, учитывая их разные соотношения размеров и материал. Так как и бронза, и медно-никелевые сплавы имеют широкий диапазон модулей Юнга, мне пришлось немного погадать (все значения указаны в ГПа):

материал диапазон (ГПа) значение (ГПа)
бронза      96 - 120        110
Cu-Ni      120 - 156        120

Далее мне нужно было разобраться с соотношением размеров. Поразмыслив над этим, я подумал, что при большем соотношении размеров (более тонкой монете) частота будет ниже, поэтому решил посмотреть, что произойдёт, если я сделаю частоту зависимой от $$. Это привело к выводу следующей формулы «ожидаемой частоты»:

$$

Выполнив расчёты с новой массой пенни (3,11 г), я получил для каждой из монет следующий график зависимости:


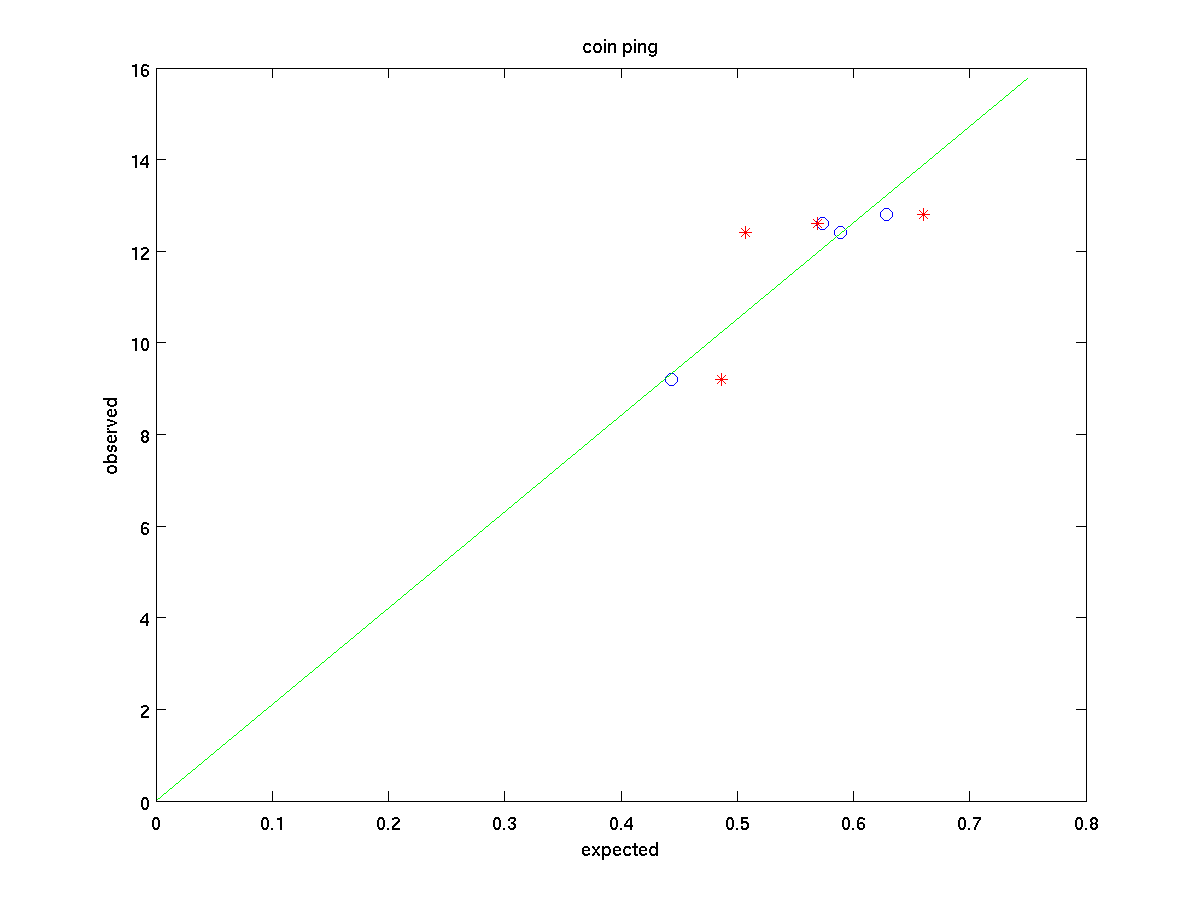
На этом графике красными звёздочками показаны числа (отмасштабированные, чтобы уместиться на том же графике), которые бы мы получили без учёта соотношения размеров; синими окружностями показаны значения с учётом зависимости от $$. Как видите, они ложатся гораздо ближе к графику. Достаточно убедительно, учитывая довольно шумные данные…

Мысли в заключение

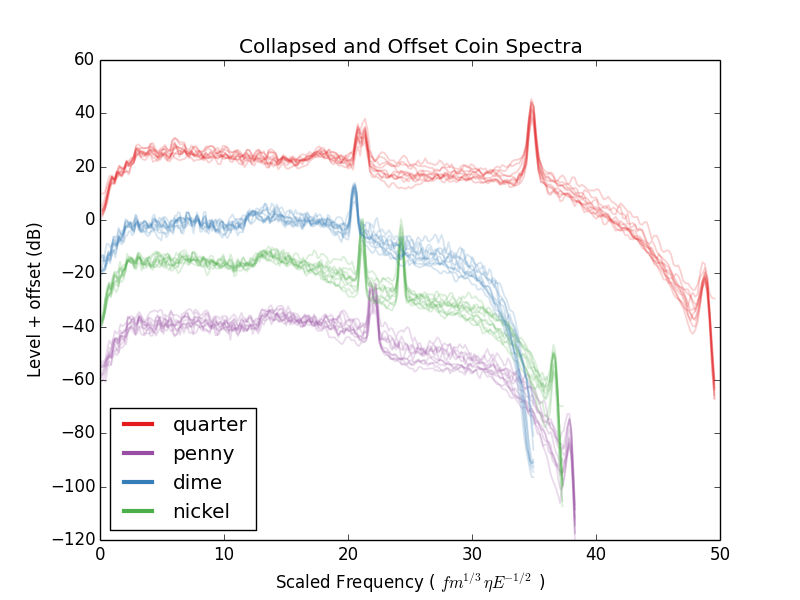
На записях звука видны множественные частоты. Некоторые из них легко объяснить, посмотрев на разные гармоники одной круглой тарелки. См. например, Waller, 1938 Proc. Phys. Soc. 50 70.

Два изображения из этой публикации:

Первая, гармоники колебаний:


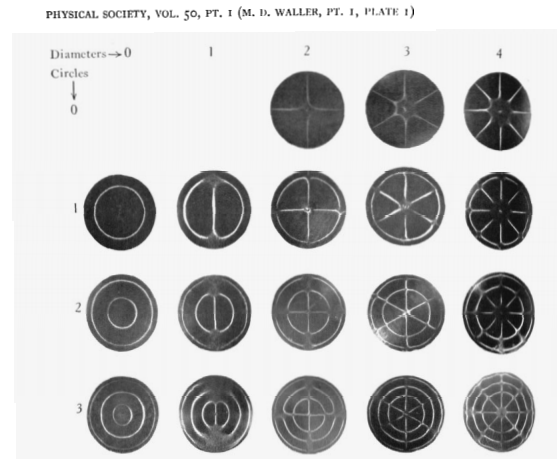
Вторая, их относительные частоты:


Это показывает нам, что первая гармоника в 1,7 раза выше, чем основная частота. Взглянув на данные, мы видим, что это и в самом деле так: в действительности для 25 центов (на графике quarter) мы даже видим вторую гармонику (в 2,3 раза выше от основной).

Вопрос разделения основной частоты немного хитрее. Если вы когда-нибудь играли с пустой кофейной кружкой, то могли заметить, что когда бьёшь по ободку, высота звука меняется в зависимости от места удара — прямо над ручкой, или смещённый на 45 градусов. Так получается, потому что есть две симметричные гармоники — там, где находится ручка, расположен узел, в другой точке расположена пучность. Последняя имеет чуть меньшую частоту.

То же самое может произойти и с 10 центами: если посмотреть на изображение монеты, изготовленной до 2005 года, можно заметить, что больше материала в направлении «север-юг» и «восток-запад». Это означает, что есть две гармоники колебаний: одна с узлами, отмеченными синим, другая — с красными:


Очевидно, что когда синие линии являются узлами, частота чуть выше.

Литература

Я нашёл статью, в которой эта тема рассматривается чуть подробнее — в целом она соответствует сказанному выше, и даже выводит очень похожие значения частот (измеренные и промоделированные). Её можно прочитать здесь: http://me363.byu.edu/sites/me363.byu.edu/files/Emerson_Steed_CoinIdentification.pdf.

Любопытно, что авторам не удалось записать звук пенни, хотя их модель предполагала, что её частота близка к той, которую замерил alemi (13,1 кГц). Они показали первую гармонику колебаний так:


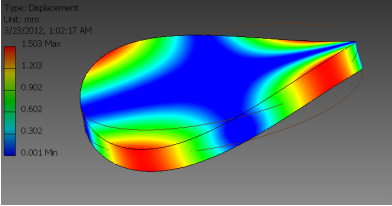
что является красивым цветным 3D-представлением гармоники, описанной в статье 1938 года Уоллером (Waller).