Обычно считается, что квантовое измерение влияет на измеряемый объект – он переходит из неопределённого состояния в определённого, как в квантовой физике суперпозиция состояний «схлопывается» в единое собственное состояние. Однако мало кто задумывается о том, что измерение также может уничтожить и квантовую информацию.
Представьте себя на месте учёного, пытающегося понять реальность на фундаментальном уровне. Как бы вы занимались этим вопросом? Вы пытались бы разбить материю на крохотные компоненты, которые легче изучать. Вы бы разрабатывали эксперименты для испытаний и измерений свойств этих крохотных субатомных частиц в различных состояниях. Если бы вы были по-настоящему хитроумным, вы бы попытались использовать измеренные вами свойства для понимания законов Вселенной.
Вы вполне могли бы решить, что, сделав достаточно измерений, или проведя достаточно экспериментов, можно узнать всё, что угодно, о любой частице (или группе частиц) во всей Вселенной. Подобные ожидания были распространены среди учёных на заре XX века. Но оказалось, что у квантовой Вселенной для нас есть другие предложения. Определенные измерения полностью сводят на нет информацию, полученную вами в предыдущих измерениях. Судя по всему, акт измерения действительно уничтожает информацию. И вот, как мы это узнали.

Определённые математические операции, например, сложение или умножение, не зависят от порядка действий – они коммутативны. Если порядок операций имеет значение, и результат зависит от него, то операции называются некоммутативными. В мире физики это очень важно.
В теории, история начинается с простой математической идеи: с понятия коммутативности. Коммутативность – это когда вы можете переставлять части местами, а результат не изменится. Сложение коммутативно: 2 + 3 = 3 + 2. То же верно и для умножения: 2 × 3 = 3 × 2. Вычитание не коммутативно: 2 — 3 ≠ 3 – 2; нужно добавить справа по минусу, чтобы выражение стало истинным. Деление тоже не коммутативно, и с ним всё немного сложнее: 2 ÷ 3 ≠ 3 ÷ 2; одну из частей нужно инвертировать, чтобы приравнять к другой.
В физике коммутативность относится не только к математическим операциям, но и к физическим манипуляциям или измерениям. Простой пример: вращения. Мы можем взять объект, отличающийся по всем трём измерениям – к примеру, сотовый телефон – и проделать одно за другим два вращения:
- держа объект перед собой, повернуть его на 90° против часовой стрелки относительно оси, направленной на вас;
- повернуть тот же объект на 90° по часовой стрелке вокруг вертикальной оси.
Кого-то может удивить, что порядок проведения этих вращений имеет значение.

Предыдущий телефон автора, из эры, предшествовавшей смартфонам, иллюстрирует некоммутативность вращений в трёхмерном пространстве. Верхний и нижний ряды, слева направо, начинают с одного и того же положения. Вверху вслед за поворотом на 90° против часовой в плоскости фотографии следует поворот на 90° по часовой вокруг вертикальной оси. Внизу те же два поворота выполнены в другом порядке. Некоммутативность вращений очевидна.
Идея некоммутативности проявляется даже в мире классической физики, однако наиболее знаменитое её приложение относится к квантовому миру в виде принципа неопределённости Гейзенберга. В нашем, классическом мире, мы можем измерить множество свойств объекта в любой момент времени. Положите объект на весы, и измерьте его массу [вес / прим. пер.]. Прикрепите на него датчик движения, и измерьте его импульс. Пульните в него лазером, и измерьте его местоположение. Отправьте в калориметр, и измерьте его энергию. Запустите таймер, пока объект колеблется, и получите период колебаний.
В квантовой Вселенной многие подобные измерения справедливы, но только в тот момент, когда вы их делаете – и не навсегда. Дело в том, что определённые квантовые свойства, которые вы можете измерить – пары величин, называемые сопряжёнными переменными – связаны друг с другом. Если с определённой точностью измерить импульс, нельзя узнать местоположение частицы точнее, чем с определённой погрешностью – даже если раньше вы измеряли это местоположение гораздо точнее.
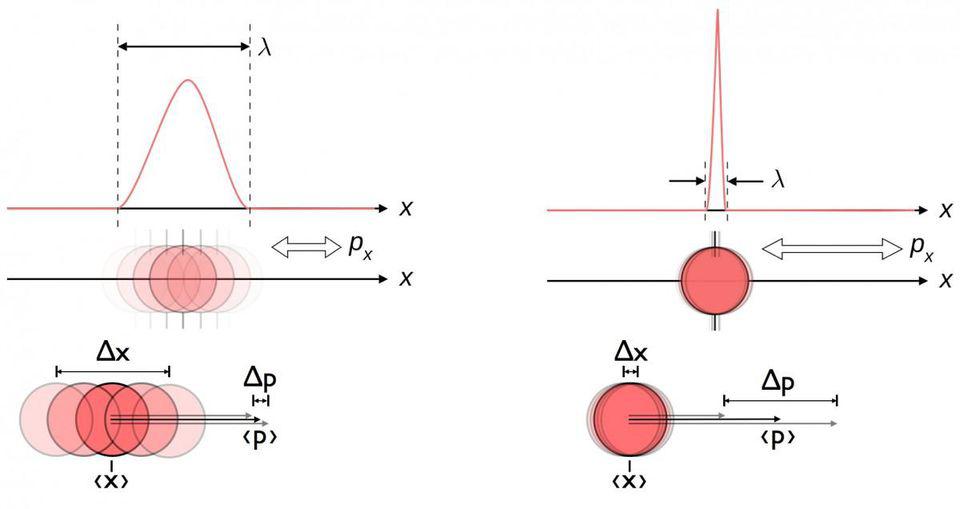
Присущая квантовому миру неопределённость между местоположением и импульсом. Чем лучше вы знаете местоположение частицы, тем хуже вы знаете её импульс – и наоборот. Местоположение и импульс лучше описываются вероятностной волновой функцией, чем единым значением.
Многим было тяжело принять принцип неопределённости, и всё же Вселенная, судя по всему, его поддерживает. Он относится и к другим парам сопряжённых переменных:
- местоположение (Δx) и импульс (Δp),
- энергия (ΔE) и время (Δt),
- электрический потенциал, или напряжение (Δφ) и свободный электрический заряд (Δq),
- угловой момент (ΔL) и ориентация, или угловое положение (Δθ).
Однако если вам действительно нужно продемонстрировать физическую необходимость, вам придётся получить подтверждающие её экспериментальные данные. Недостаточно просто заявить «не знаю, какая точность у моих измерений». Нужно найти способ показать, что информация, полученная вами в предыдущих измерениях с определённой точностью, была уничтожена последовавшими измерениями.
И в 1921 году физик Отто Штерн придумал гениальный способ это проверить.

У отдельных и составных частиц может быть как орбитальный, так и собственный (спиновой) момент импульса. Когда у этих частиц есть внутренний или присущий им электрический заряд, появляется магнитный момент, заставляющий их отклоняться на определенную величину в присутствии магнитного поля.
Допустим, у вас есть квантовая частица – электрон, протон, композитное ядро (объект, состоящий из связанных протонов и нейтронов), или даже нейтральный атом с ядром и вращающимися вокруг него электронами. У такого объекта есть несколько присущих ему квантовых свойств: масса, электрический заряд, и т.п. В теории у него должен быть и момент импульса — не только из-за того, что он вращается вокруг других частиц (или вокруг него вращаются другие частицы), но и некий присущий ему, внутренний момент импульса. Это квантовое свойство объекта называется спином [to spin (англ.) – вращаться / прим. пер.], по аналогии с волчком, вращающимся вокруг собственной оси.
Если представить себе волчок, то можно сразу придумать два способа его вращения:
- по часовой стрелке вокруг вертикальной оси,
- или против часовой стрелки.
Живя в мире без гравитации (и без предпочтительных направлений – каковую роль, в нашем случае, играет направление к центру Земли), можно было бы представить его вращение по или против часовой стрелки вокруг любой оси во всех трёх измерениях. Такова наша посылка: идея о существовании у частиц спина, внутреннего момента импульса. Хотя в 1921 году оставалось ещё несколько лет до того, как Джордж Юджин Уленбек и Сэмюэл Абрахам Гаудсмит сформулировали свою гипотезу о спине электрона, эта идея всё равно присутствовала в «старой квантовой теории» Бора и Зоммерфельда.

На траекторию прохождения обладающей спином квантовой частицы через магнитное поле влияет её магнитный момент, связанный с её спином. В квантовой теории это означает, что спин должен быть дискретным.
Как измерить спин квантовых частиц? Как определить, является ли спин непрерывной величиной, способной принимать любое значение на манер классических параметров, или же он по сути своей квантовый и дискретный?
Штерн догадался, что если взять магнитное поле, перпендикулярное направлению движения заряженной частицы со спином, поле будет воздействовать на траекторию движения в соответствии с магнитным моментом, связанным со спином. На частицу без спина это не повлияет, а частица со спином отклонится в направлении магнитного поля.
Если спин дискретный, т.е., квантуется, все частицы, движущиеся с одной скоростью, должны оказаться в одном месте. Если спин классический и непрерывный, частицы могут оказаться где угодно.

Луч частиц, проходящих через магнит, может дать квантовые/дискретные результаты (5) для момента импульса частиц, или же классические/непрерывные (4). Опыт Штерна — Герлаха продемонстрировал существование нескольких важнейших квантовых явлений.
В 1922 году физик Вальтер Герлах устроил проверку идей Штерна, разработав эксперимент. Герлах начал с электромагнита, через который проходит луч атомов серебра, которые легко разгонять до одинаковых скоростей. Когда электромагнит был выключен, все атомы серебра попадали в одно и то же место детектора, расположенного с другой стороны магнита. Когда магнит включали, луч разделялся на две части – половина атомов изменяла траекторию, отклоняясь в одну сторону, половина – в другую. Сегодня известно, что это поведение соответствует наличию спинов +1/2 и -1/2, направленных параллельно или антипараллельно линиям магнитного поля.
Этого раннего эксперимента было достаточно для доказательства существования спина, который квантуется на дискретные значения. Однако далее была продемонстрирована способность квантовой механики уничтожать полученную ранее информацию. Когда атомы серебра проходят через аппарат Штерна-Герлаха с включённым магнитным полем, то луч атомов разбивается на два, в соответствии со спинами частиц.
Хорошо – а что, если мы пропустим одну из половин луча через ещё один аппарат Штерна-Герлаха?

Если выстрелить частицами сквозь аппарат Штерна-Герлаха, магнитное поле разделит их луч на две части, в соответствии с возможными вариантами спина. Если поставить на пути одной из половин луча второй аппарат Штерна-Герлаха, расщепления уже не произойдёт, поскольку это квантовое свойство частиц уже было определено.
Ответ может вас удивить: всё зависит от того, в каком направлении будет ориентирова магнит. Если первый аппарат Штерна-Герлаха был ориентирован, допустим, по оси х, то часть частиц отправится по направлению +х, а часть – по –х. Сконцентрируемся на первых. Если провести их ещё через один магнит, ориентированный по оси х, частицы разделятся не будут – они все останутся ориентированными в направлении +х.
Но если сориентировать второе магнитное поле по оси у, результат вас может удивить. Теперь луч частиц, изначально ориентированных по направлению +х, расщепится по оси у: половина пойдёт по направлению +у, а вторая – по направлению –у.
Дальше наступает критический момент: что будет, если мы сконцентрируемся только на частицах +у, и снова пропустим их через магнитное поле, ориентированное по оси х?
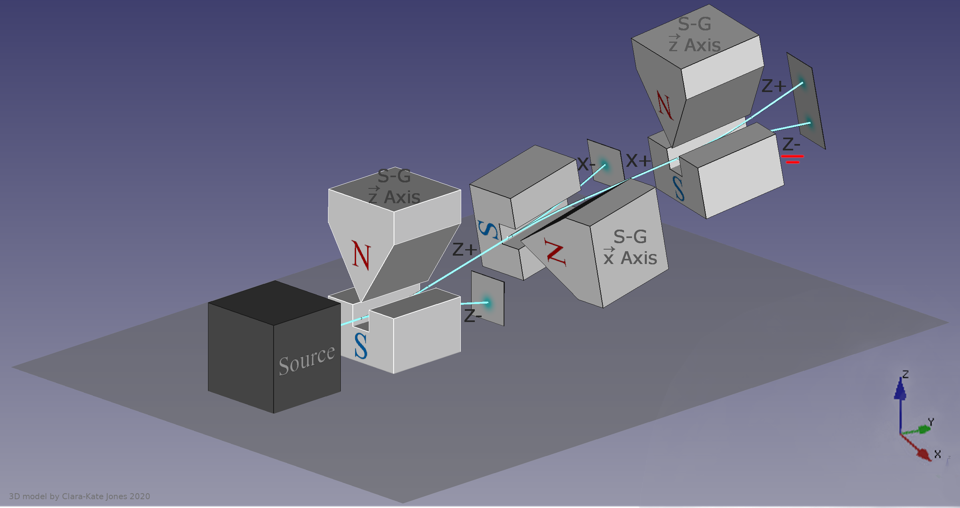
Если пропустить набор частиц через аппарат Штерна-Герлаха один раз, они разделятся соответственно спину. Если пропустить их через второй, перпендикулярный магнит, они разделятся в новом направлении. Если задействовать третий магнит, параллельный первому, они снова разделятся – что означает, что определённая ранее информация снова стала случайной из-за самого последнего измерения.
Они снова, как в первый раз, разделятся по направлениям +х и –х. Пропуская их через второй магнит, ориентированный перпендикулярно, вы уничтожили информацию, полученную при первом измерении. Сегодня мы понимаем, что направления х, у и z не коммутируют друг с другом. Квантовое измерение переменной одного типа уничтожает всю предыдущую информацию о сопряжённых с ней переменных.

Несколько последовательных аппаратов, расщепляющих квантовые частицы по одной из осей согласно их спину, будут расщеплять их по перпендикулярному предыдущему направлению, но не будут расщеплять по тому же направлению.
У эксперимента Штерна-Герлаха осталось одно долгоиграющее последствие. В 1927 году было показано, что расщепление происходит даже у атомов водорода, что говорит о наличии у них ненулевого магнитного момента. У атомных ядер есть присущий им квантовый момент импульса, и они тоже расщепляются в аппарате Штерна-Герлаха. Меняя магнитное поле по времени, учёные поняли, как заставить магнитный момент принимать одно или другое состояние. Оказалось возможным вызывать переходы между состояниями, меняя по времени поле. Так родился магнитный резонанс, использующийся сегодня повсеместно в аппаратах МРТ, и в итоге это привело к появлению атомных часов.

Современный МРТ-сканер с полем высокой напряженности. Эти машины сегодня являются основными потребителями гелия. В своей работе они используют квантовые переходы спина в субатомных частицах. Физику их работы открыли ещё в 1937 году, обнаружив, что переменные поля возбуждают осцилляции Раби.
Казалось бы – акт измерения и наблюдения не должен влиять на результат опыта. Идея о том, что наблюдение за системой изменяет её свойства, кажется абсурдной. Но в квантовой Вселенной это не только происходит – это продемонстрировали ещё до того, как теория была полностью сформирована. Измерение спина частицы вдоль одного направления уничтожает полученную ранее информацию касательно двух других направлений. Даже если вы измерили их раньше и точно их знаете, новое измерение фундаментально стирает (рандомизирует) любую полученную ранее информацию.
Многим физикам, услышавшим знаменитое высказывание Эйнштейна о том, что "Бог не играет в кости со Вселенной", в качестве контрпримера в первую очередь в голову должен приходить именно этот эксперимент. Неважно, насколько хорошо, по вашему мнению, вы понимаете реальность. Неважно, насколько точно и тщательно вы разными способами её измеряете. Любое измерение по сути своей рандомизирует часть информации, полученной ранее. Новое измерение действительно уничтожает старую информацию. Всё, что нужно для доказательства этого – магнит и немного частиц.




