NaN все еще может немного удивить

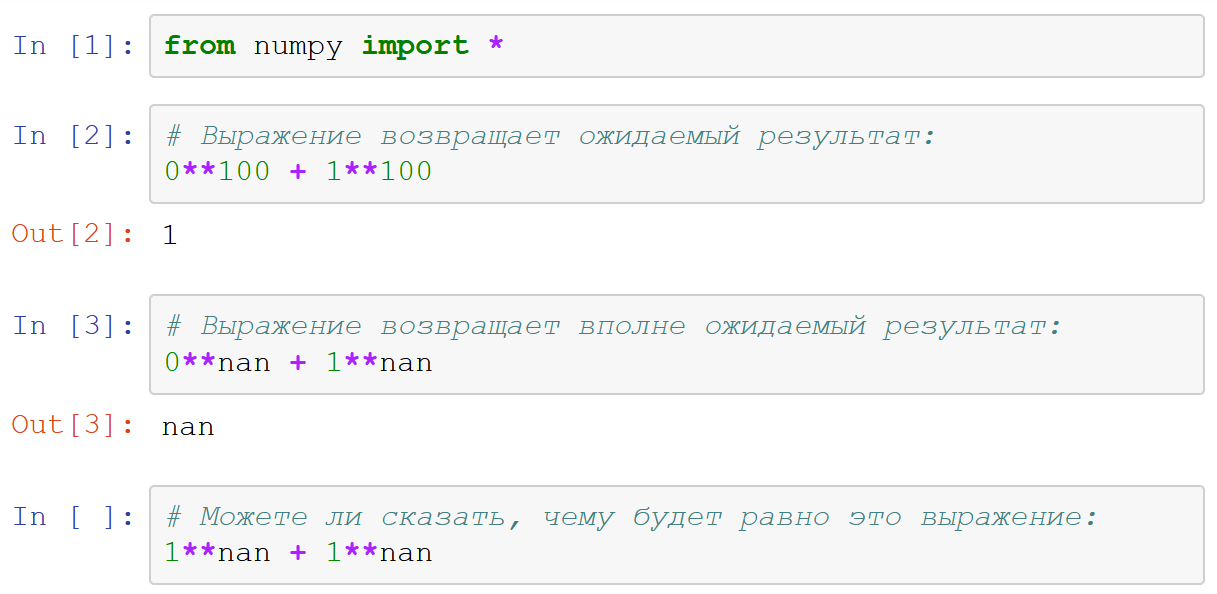
Сначала, я подумал, что это очередной вопрос из тех, которые могут задаваться на собеседовании. Наверное, если как следует пораскинуть мозгами, то можно догадаться до того, каким будет результат. Откинувшись на спинку кресла, начал размышлять, включать логику, вспоминать что-нибудь, на что можно опереться в рассуждениях. Но тщетно! Вдруг стало совершенно очевидно, что найти ответ не удается. Но почему? В чем нужно разбираться, чтобы он был найден? В математике? В языке программирования?

Ответ должен быть NaN. Но почему я не уверен в этом? Всю дорогу была уверенность в том, что любые выражения, содержащие NaN, вернут NaN. Ну разве что только если поделить NaN на ноль — в этом случае будет вызвано исключение ZeroDivisionError. Сто процентов NaN!

Ввожу выражение в ячейку блокнота:

>>> 1**nan + 1**nan
2.0

В самом деле? Постойте:

>>> arange(5)**nan
array([nan,  1., nan, nan, nan])

То есть, по какой-то причине, единица в степени NaN — это единица, а вот ноль и все остальные числа в степени NaN — это NaN. Где логика? В чем дело?

Так, давайте еще раз:

>>> 0**nan, 1**nan
(nan, 1.0)

Может быть я просто из-за отсутствия какой-то практической надобности в глубоких познаниях о NaN, просто о чем-то не подозревал? А может я знал, но забыл? А может еще хуже — я не знал и забыл?

Заходим на Википедию. Там данный вопрос тоже обозначен как проблема, но почему все именно так устроено, никак не объясняется. Зато узнал что:

>>> hypot(inf, nan)
inf

Хотя, в то же время:

>>> sqrt(inf**2 + nan**2)
nan

Что, согласитесь, тоже немного странно.

Ладно, с Википедии отправляемся в C99 на 182 страницу и наконец-то получаем логическое объяснение, почему pow(x, 0) возвращает 1 для любых x, даже для x равного NaN:

>>> power(nan, 0)
1.0

Если функция $$ возводится в степень $$ и при этом $$ стремится к 0, то в результате получится 1, вне зависимости от того, какое значение имеет $$.



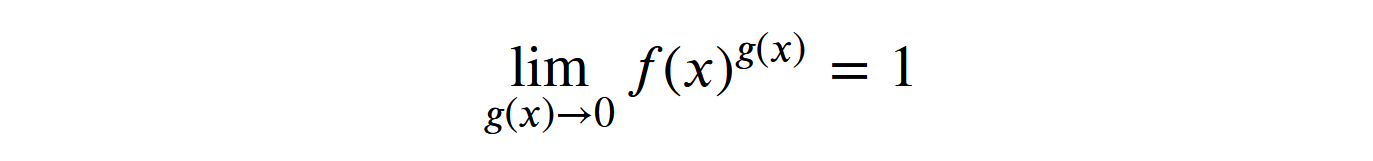
А если результат не зависит от числового значения функции $$, то 1 — является подходящим результатом, даже для NaN. Однако это по-прежнему не объясняет, почему 1 в степени NaN равна 1.

Отыскиваем еще один C99 и на 461 странице не видим никаких объяснений, просто требование того, что pow(+1, y) должно возвращать 1 для всех y, даже равных NaN. Все.

С другой стороны, объяснение, почему pow(NaN, 0)=1 является более предпочтительным, чем pow(NaN, 0)=NaN все-таки наталкивает на мысль о том, что NaN не стоит воспринимать буквально, как Not-a-Number. Допустим, в результате каких- то вычислений мы получили число, превышающее размер памяти, выделенный под данный тип чисел, например:

>>> a = pi*10e307
>>> a
inf

В результате мы получили inf, что именно это за число мы не знаем, но все же это какое-то число. Затем мы снова что-то вычислили и снова получили слишком большое число:

>>> b = e*10e307
>>> b
inf

Разность a и b вернет NaN:

>>> c = a - b
>>> c
nan

Единственная причина, по которой мы можем считать c не числом, заключается в том, что мы использовали недостаточно точные вычисления. Однако, в c под NaN все же скрывается какое-то значение. О том, что это за значение, мы не знаем. Но все же это число, а раз это число, то нет ничего удивительного в том, что pow(1, NaN)=1.

Почему же тогда pow(0, NaN)=NaN? Дело в том, что если возвести 0 в любую степень, то мы действительно получим ноль. Кроме одного единственного случая — когда степень равна 0:

>>> 0**0
1

Из-за чего в выражении pow(0, NaN) появляется неопределенность с конкретным значением NaN. Конечно, вероятность того, что под NaN может скрываться 0 — исчезающе мала и можно было бы принять, что pow(0, NaN)=0. Но все же лучше перестраховаться, мало ли к чему это может привести. Возможно, так и рассуждали, когда создавались стандарты.

Даже не знаю, что еще сказать… если вы заранее знали ответ, то скорее всего вам можно позавидовать, ведь сферы, где могут пригодиться такие познания, наверняка, переполнены интересными задачами. А может и наоборот. Напишите об этом в комментариях.

P.S. Поскольку NaN относится к числам с плавающей точкой, оно может быть ключом словаря:

>>> d = {0.1: 'a', nan: 'b'}
>>> d[nan]
'b'

Имеет ли смысл использовать такое на практике? Думаю, что лучше не стоит.