Продолжаем изучать нечеткую логику по книге Гостева В.И «Нечеткие регуляторы в системах автоматического управления». После того, как мы насладились прекрасными видами поверхностей отклика, перейдем непосредственно к решению очередной задачи из книги Гостева В.И «Нечеткие регуляторы в системах автоматического управления».
Этот текст является продолжением предыдущих публикаций:
- Простой регулятор на базе нечеткой логики. Создание и настройка.
- Нечеткая логика в красивых картинках. Поверхности отклика для разных функций принадлежности.
- Создание регулятора на базе нечеткой логики с многоканальной настройкой.
- Простая нечеткая логика слеплена «из того что было» для газотурбинного двигателя.
- Нечеткая логика против ПИД. Скрещиваем ежа и ужа. Авиадвигатель и алгоритмы управления АЭС.
Тем, кто незнаком с нечеткой логикой рекомендую сначала ознакомится с первым текстом, после этого все что изложено ниже будет просто и понятно.
Сразу должен предупредить, у меня получился очередной пост унижения традиционного ПИД-регулятора со стороны нечеткой логики. Это не потому, что я специально старался. Должен ответственно заявить, что в исходной книге нет сравнения качества управления ПИД и Fuzzy. Все сравнения я выполнял сам, по собственной воле, в трезвом уме и ясной памяти. И, да, мне не платили наймиты мировой буржуазии, распространяющие нечеткую логику, как продажную девку империализма.
Возможно, задачи в книге специально подобраны так, что нечеткие регуляторы подходят лучше для управления, чем классический ПИД.
Далее под катом – ПИД-регулятор, нечёткая логика и конечные автоматы для управления газотурбинным двухроторным двигателем (ГТД). Тем, кто впервые планирует познакомиться с работой нечеткой логики, рекомендую начать со статьи «Простой регулятор на базе нечеткой логики. Создание и настройка»
Линейную модель двухроторного ГТД, работающего на базовом режиме малого газа, вместе с исполнительным механизмом можно представить в виде структурной схемы, изображенной на рисунке 1 (параметры передаточных функций модели ГТД в структурной схеме указаны на рисунке).
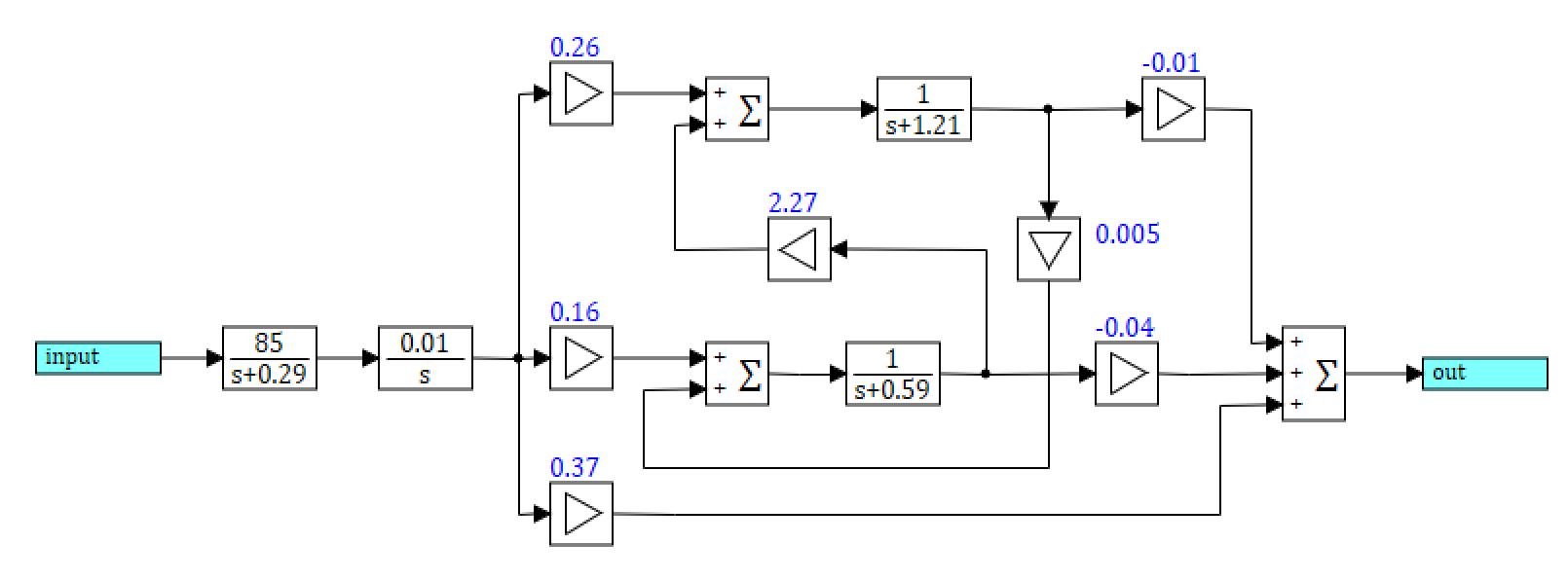
Рисунок 1. Модель ГТД в режиме малого газа.
Моделировать мы будем отработку единого возмущения.
В начальный момент времени система находится в нулевом состоянии. В момент времени 1 сек. система подвергается возмущению, которое скачком изменяет выходную величину объекта управления. Задача системы – быстро компенсировать возмущение и привести систему в первоначальное, устойчивое состояние.
Автор книги предлагает использовать два регулятора: один – для быстрого парирования возмущения, другой – для точного управления при малых отклонениях. При больших отклонениях работает первый регулятор, как только отклонение становится меньше 0.009 включается второй регулятор.
Как и в предыдущих статьях, для анализа эффективности мы будем сравнивать результаты с эталонным ПИД-регулятором.
Общая схема объекта вместе с системой управления будет выглядеть так, как показано на рисунке 2. Усилитель со значением – 20, модель исполнительного механизма (опять-таки взятая «as is» из книги В.И. Гостева).
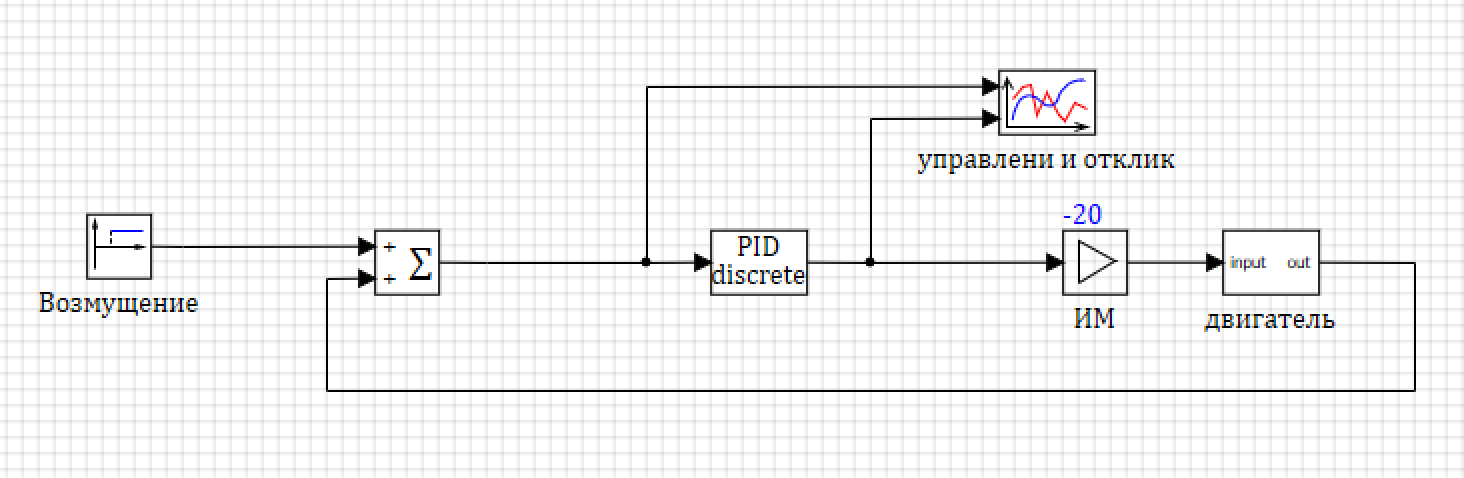
Рисунок 2. Двигатель с системой управления.
На этом рисунке в качестве регулятора мы используем дискретный ПИД-регулятор с периодом дискредитации 0.001 сек и постоянной времени дифференцирования 0.001.
Запустим систему со значениями настроек ПИД-регулятора 1,1,1 для всех коэффициентов. Результат представлен на рисунке 3.
Из рисунка видно, что дискретный ПИД с единичными коэффициентами, при скачке на 1 выдал в качестве управляющего воздействия величину 1000, что соответствует постоянной времени дифференцирования 0,001. Дискретный ПИД рассчитывает скорость как разность входа между двумя отсчетами, деленную на постоянное время дифференцирования. Если отмасштабировать график, по оси У от -1 до 1 видно, что ПИД по умолчанию сработал и привел систему к 0 за 7 секунд.
 |
 |
| Рисунок 3. Управляющее воздействие и отклик системы. | |
Например, воздействие на модель с величиной 1000, полученное после ПИД, возможно в жизни? Неизвестно. Если это подача топлива, то, очевидно, что система подачи не сможет запихнут в 1000 раз больше топлива чем, в режиме малого газа.
Можно предположить, что воздействие ограничено сверху и снизу значениями 10, -10. Цифра взята произвольна. Для анализа работы системы управления она не важна, зато позволит меньше менять масштабы графика с результатом. В этом случае схема будет выглядеть следующим образом:

Рисунок 4. Схема управления с ограничителям входного воздействия.
Ограничивая воздействие, изменяем переходной процесс, увеличивая перерегулирование и время переходного процесса (рисунок 5). Поскольку вместо 1000, выдаваемой ПИД на первом шаге скачка возмущения, в исполнительный механизм передается только 10.
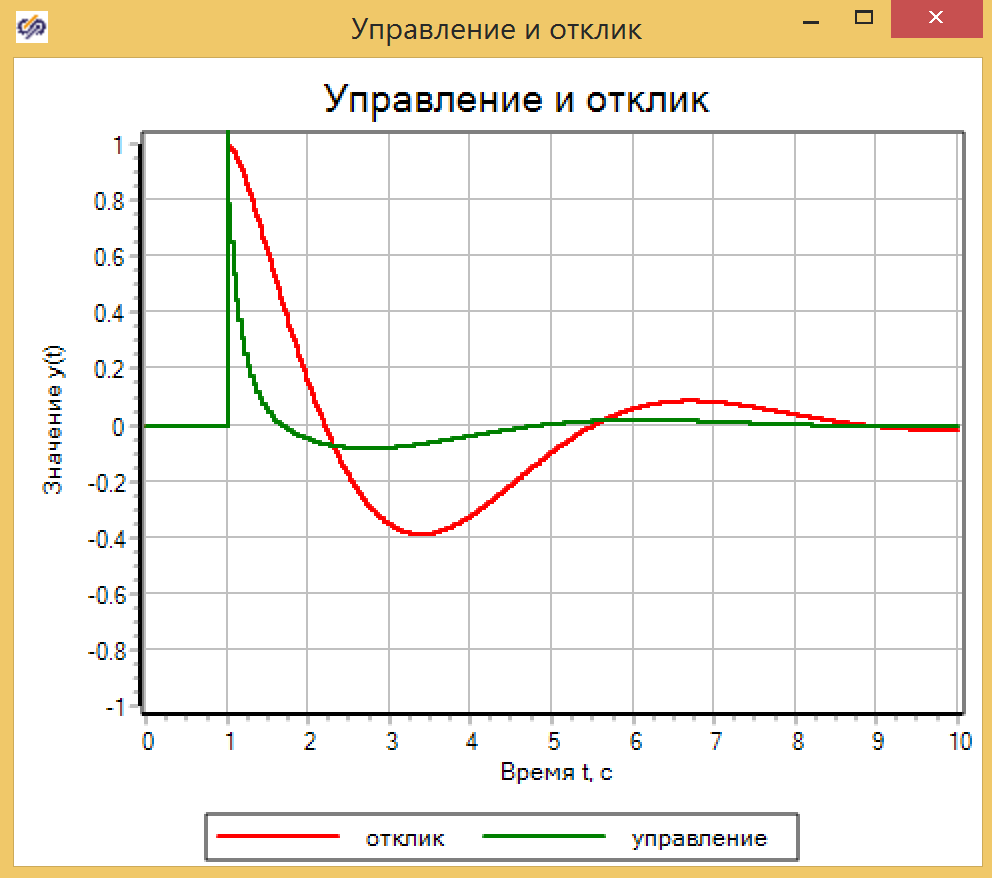
Рисунок 5. Переходной процесс с ограничителем управляющего воздействия.
Настройка ПИД регулятора с помощью оптимизации
Давайте теперь настроим регулятор с использованием блока оптимизации.
Cубмодель оптимизации подключаются ко входу в контроллер управления. И получается значение отклонение от 0
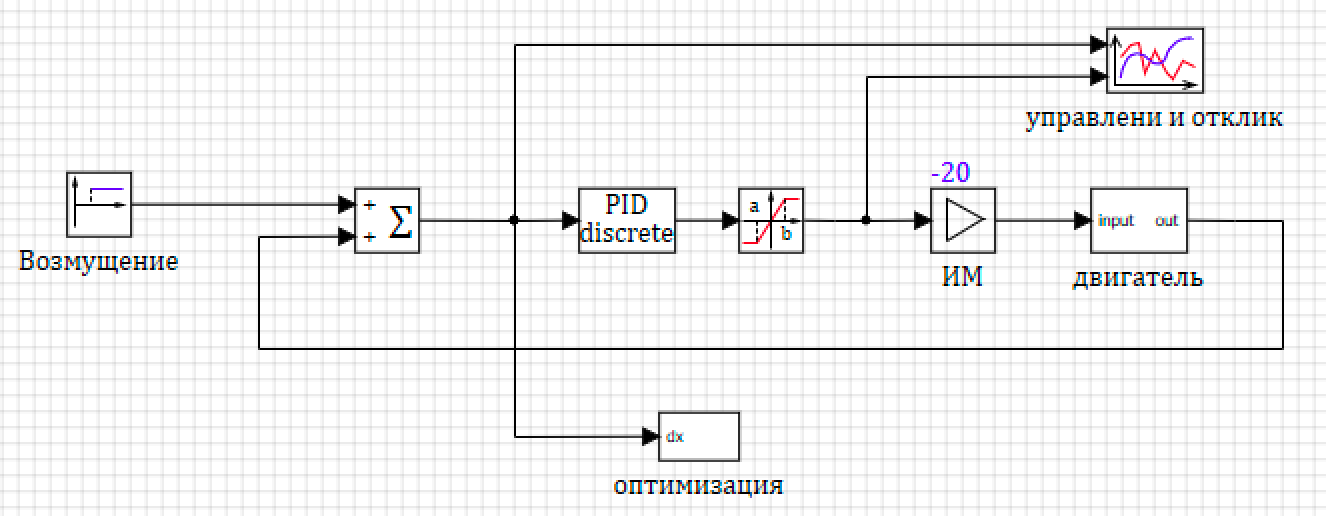
Рисунок 6. Подключение блока оптимизации.
Схема субмодели оптимизации ПИД представлена на рисунке 7.
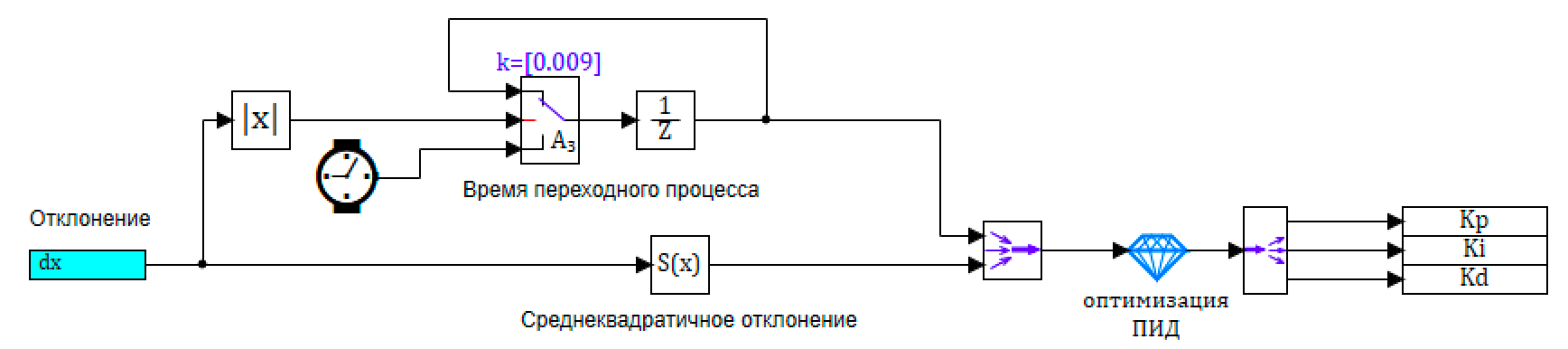
Рисунок 7. Блок оптимизации..
Рассмотрим работу блока оптимизации. В качестве параметров оптимизации используются:
— время переходного процесса – время, в течение которого в переходном процессе отклонение больше 0.009.
— среднеквадратичное отклонение на всем протяжении процесса.
Модуль отклонения направляется на управляющий контакт переключателя блока «Ключ-3» Переключатель работает в зависимости от величины модуля отклонения. Если модуль больше заданного порога, то переключатель подключен ко второму входу, куда подается текущее время, на входе — текущее время модели.
Далее находится блок «Запаздывание на период квантования» получающий сигнал с предыдущего шага и отправляющий его обратно на первый вход переключателя.
Как только модуль отклонения становится меньше порога, переключатель соединяет выход с сигнала первого входа, где у нас находится модельное время с предыдущего шага. Если в процессе расчёта модуль отклонения снова превысит пороговое значение, то в блок задержки будет передаваться текущее модельное время.
Таким образом, в результате работы этой конструкции у нас в блоке «Запаздывание на период квантования» хранится последнее время, когда отклонение было больше заданного, т.е. время переходного процесса.
Сигнал, полученный из модели, направляется на блок расчёта среднеквадратичного отклонения. Чем меньше среднее отклонение в переходном процессе, тем оптимальнее регулятор.
Минимизируя среднеквадратичное отклонение по всему процессу, мы настраиваем точность регулирования. Без данного критерия возможно решение, когда система, попадая в заданную трубку, продолжает колебаться уже в переделах этого лимита.
Настройки блока оптимизации представлены на рисунке 8.

Рисунок 8. Настройки блока оптимизатора.
Оптимизацию осуществляем по полному переходному процессу. Это означает, что последовательно запускается несколько десятков или сотен расчётов, в каждом из которых подбирается вектор из трех параметров и подается на выход. На выходе из блока оптимизации эти параметры записываются в сигналы проекта Кp, Ki, Kd (см. рис. 7 и рис. 8). А сигналы проекта используются в настройках блока дискретного ПИД-регулятора. (рис. 10.)
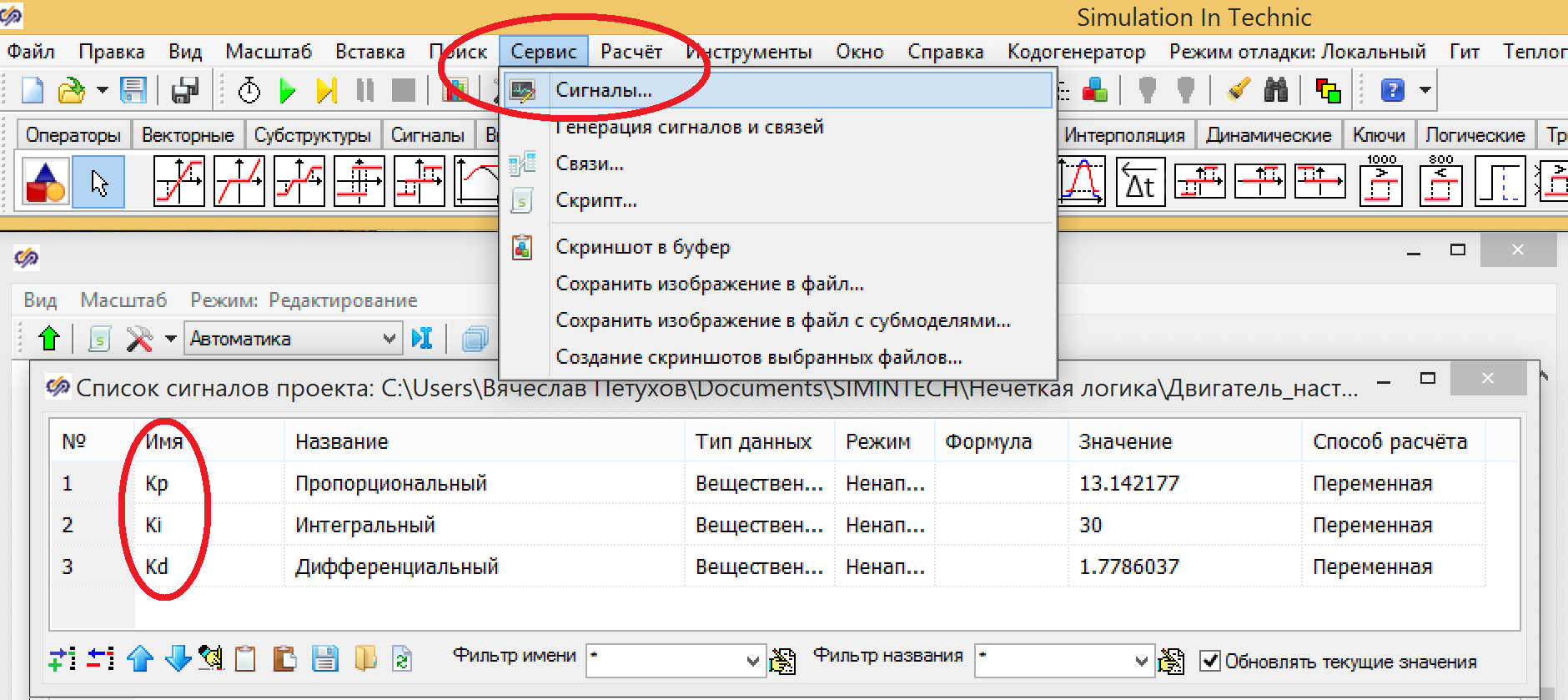
Рисунок 9. Задание сигналов проекта для настройки ПИД.
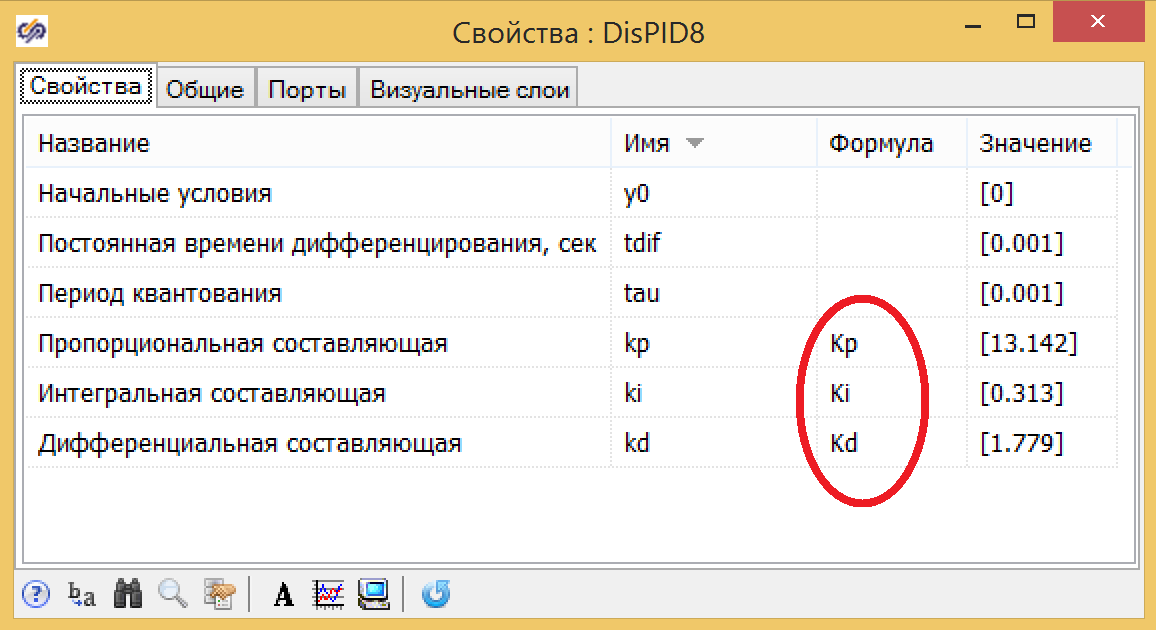
Рисунок 10. Настройка параметров ПИД-регулятора.
В результате выполнения процесса оптимизации получаются следующие значения оптимальных параметров:
Kp = 13.142
Ki = 0.313
Kd = 1.779
Время переходного процесса составляет 0.72 сек. Процесс регулирования оптимального регулирования предоставлен на рисунке 11.
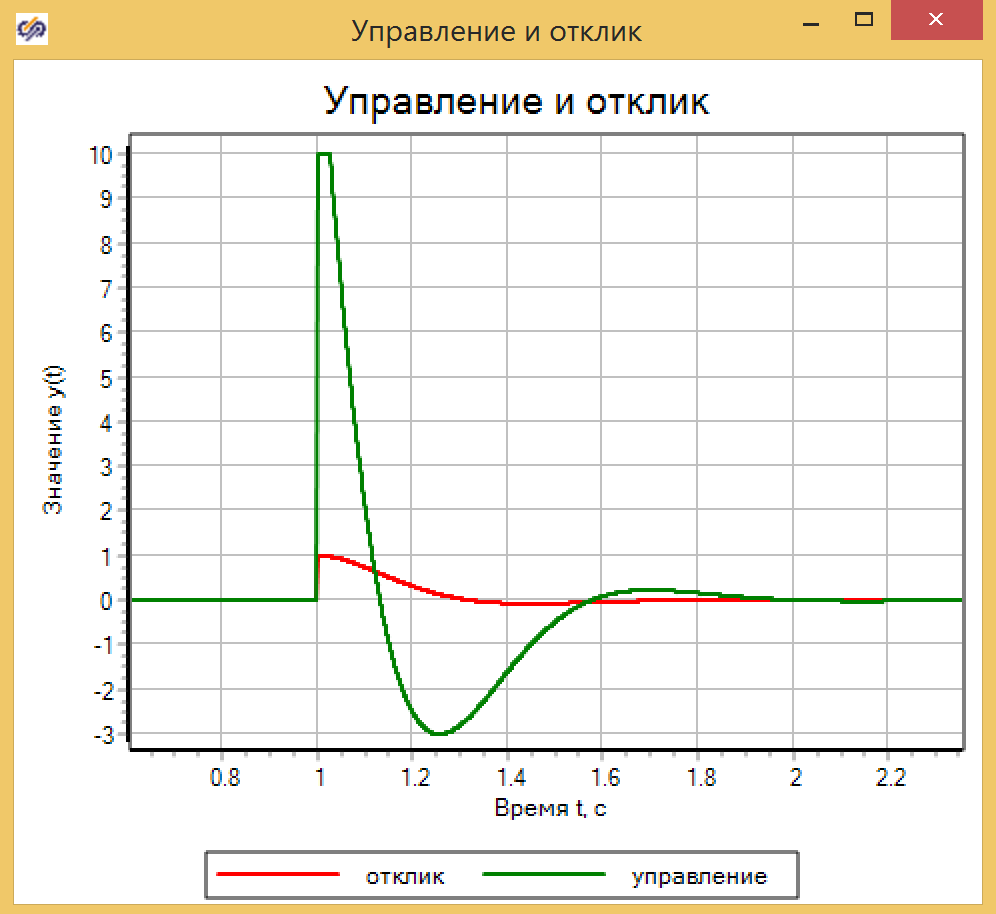
Рисунок 11. Переходной процесс с оптимизированным ПИД-регулятора.
Получив эталонную систему для сравнения, переходим к настройке нечетких регуляторов.
Настройка первого нечеткого регулятора
Первый нечеткий регулятор должен вернуть систему после скачка на 1 насколько возможно быстро обратно, к нулевому состоянию. В качестве входных параметров у нас будет само отклонение и скорость изменения отклонения.
Входящие сигналы отклонение и скорость изменения отклонения, проходя через блоки фазификации, раскладываются на три терма каждый. С помощью функций принадлежности Гаусса.
Отклонение – больше, норма, меньше.
Скорость изменения – растет, не изменяется, падает.
Регулятор будет выдавать воздействие, когда появляется отклонение, а так же когда скорость изменения регулятора показывает, что отклонение будет увеличиваться (даже если в данный момент оно в норме). База правил для регулятора:
- если отклонение больше или (отклонение норма (0) и скорость растет), то воздействие больше.
- если отклонение в норме, то воздействие 0.
- если отклонение меньше или (отклонение норма (0) и скорость падает), то воздействие меньше.
Модель такого регулятора, собранного в виде структурной схемы, представлена на рисунке 12.

Рисунок 12. Модель первого регулятора на базе Fuzzy Logic.
Фазификация входных переменных осуществляется с помощью функции Гаусса. Чтобы сократить количество настраиваемых переменных, принимаем диапазон изменения входных переменных и выхода регулятора симметричный относительно 0, тогда достаточно одного числа для задания диапазона фазификации. Для настройки такого регулятора нам необходимо определить всего три числа:
- uMax_1 – максимальное значение выхода регулятора;
- deltaMax_1 – максимальное отклонение;
- divMax_1 – максимальная произведенная.
Данные переменные помещаются в сигналы проекта – см. рисунок 13.
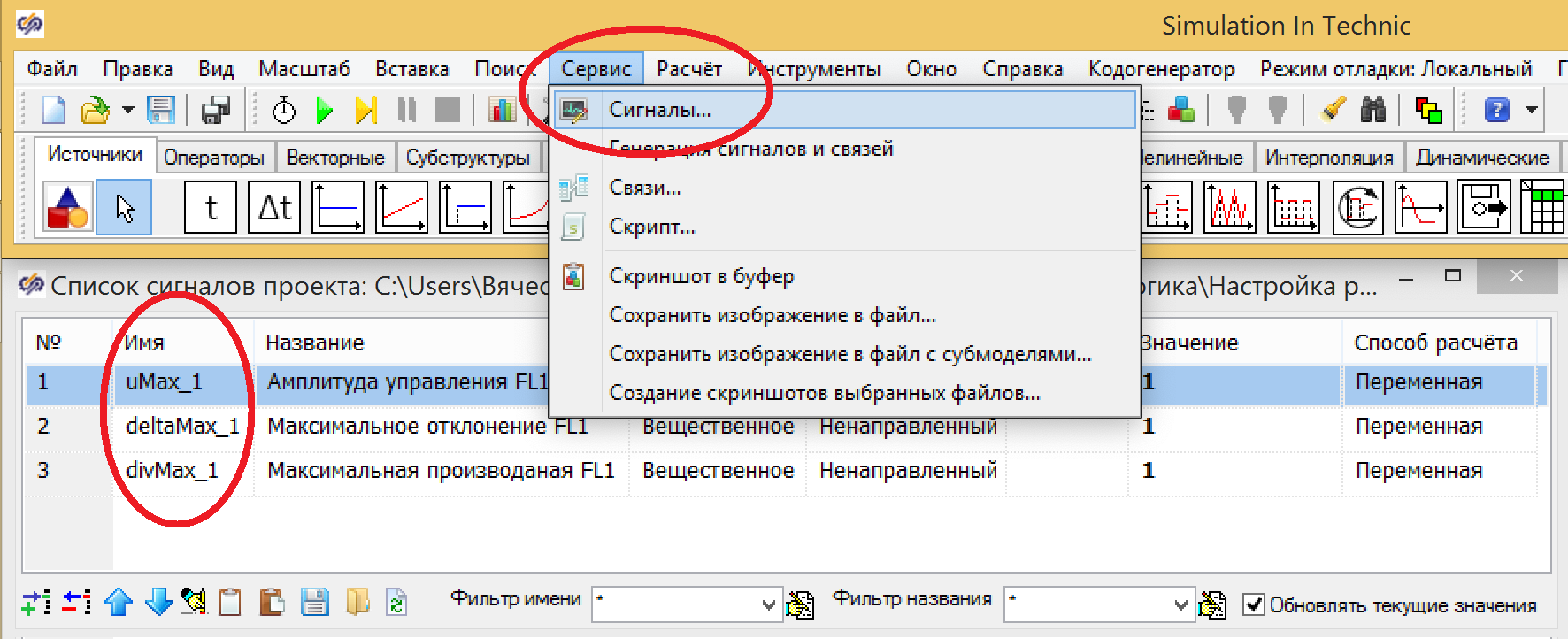
Рисунок 13. Настройка блока фазификации для скорости изменения.
Для формирования параметров фазификации мы делим диапазон (–uMax_1… uMax_1) на три части и получаем вектор вершин [–uMax_1 ,0, uMax_1], а в качестве среднеквадратичного отклонения выбираем расстояние между вершинами, деленное на 2. (см. предыдущий текст, где мы экспериментировали с параметрами функции фазификации).
В итоге, свойства блока фазификации скорости выглядят так:
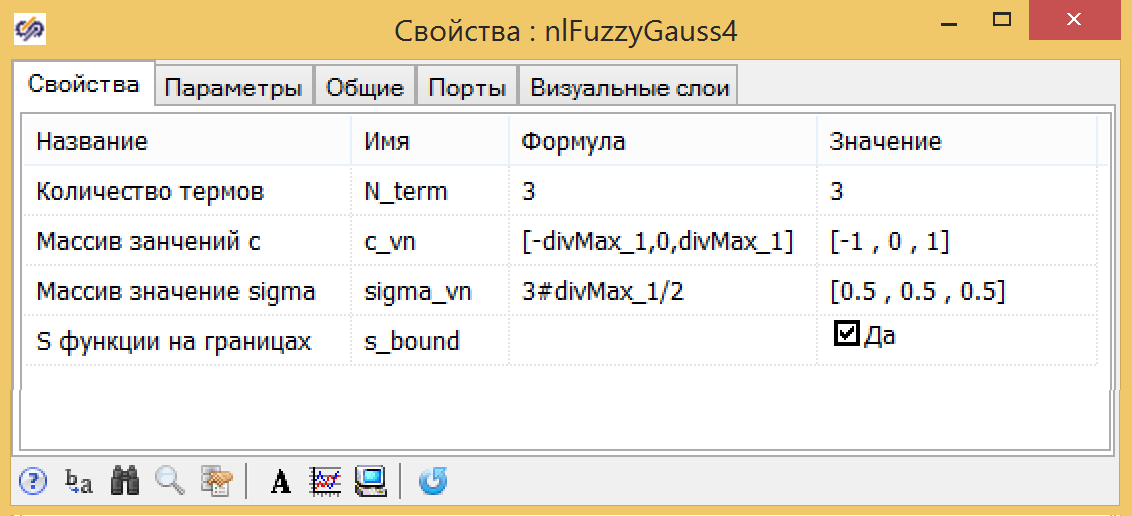
Рисунок 14. Настройка блока фазификации для скорости изменения.
Именно такой регулятор мы строили в прошлой статье и смотрели на его поверхность отклика.
Поскольку у нас в задаче будет два регулятора, вычисление скорости изменений выносим в отдельный блок и выполняем простой разностной схемой:
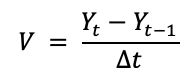 , где:
, где: Yt — текущее значение;
Yt-1 — значение на предыдущем шаге;
Δt = 0.001 – шаг по времени такой же, как при дискретизации дискретного ПИД-регулятора.
Схема показана на рисунке 15. Деление на Δt учитывается в блоке сравнения, где можно задать коэффициенты для каждого входа.
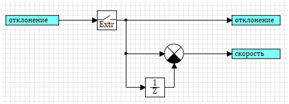
Рисунок 16. Схема вычисления скорости изменения.
Поскольку вся схема у нас уже готова, остаётся заменить ПИД-регулятор на FL -регулятор (см. рисунок 17) и посмотреть, что получается.
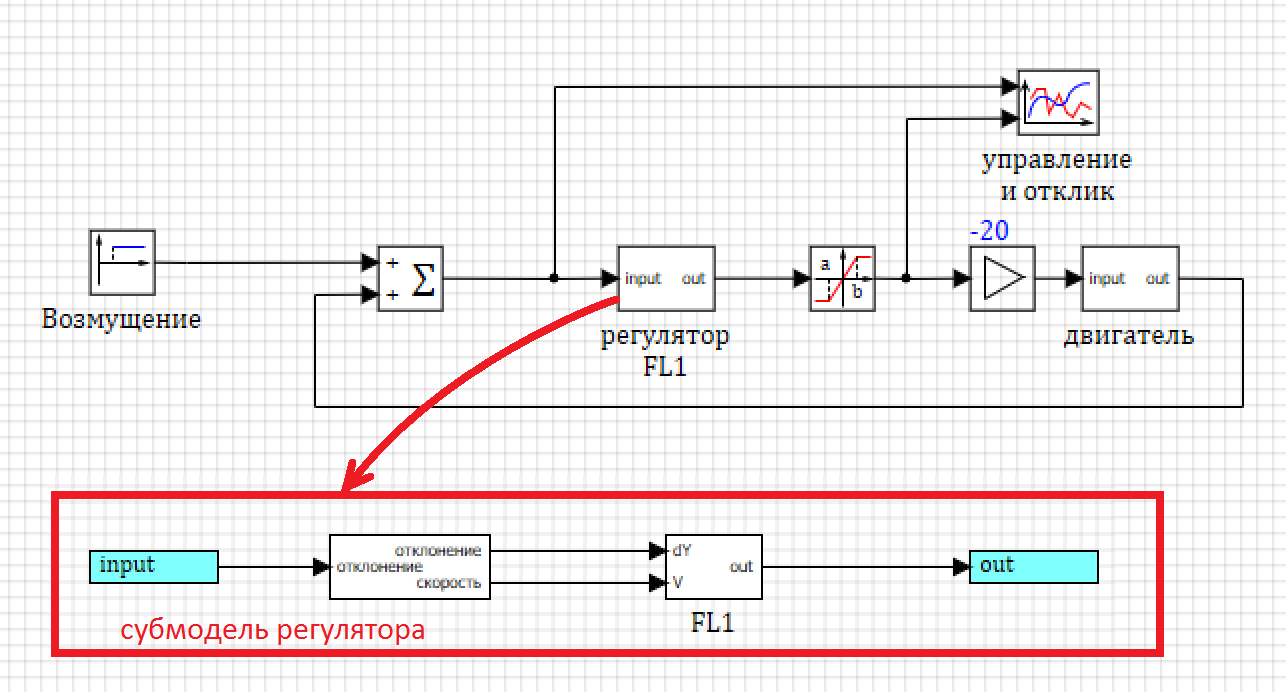
Рисунок 17. Схема модели с одним нечетким регулятором.
И опять, к моему немалому удивлению, нечеткий регулятор справился лучше, чем ПИД, при начальных единичных настройках. Какая-то сплошная реклама нечеткой логики получается.
При чем, если в предыдущих случаях можно было списать на то, что в нечетком регуляторе используется вторая производная, то в данном случае этот нечеткий регулятор использует ту же самую производную, а ПИД использует еще интегральную составляющую.
 ПИД регулятор |
 FL регулятор |
| Рисунок 18. Переходной процесс при единичных настройках регуляторов. | |
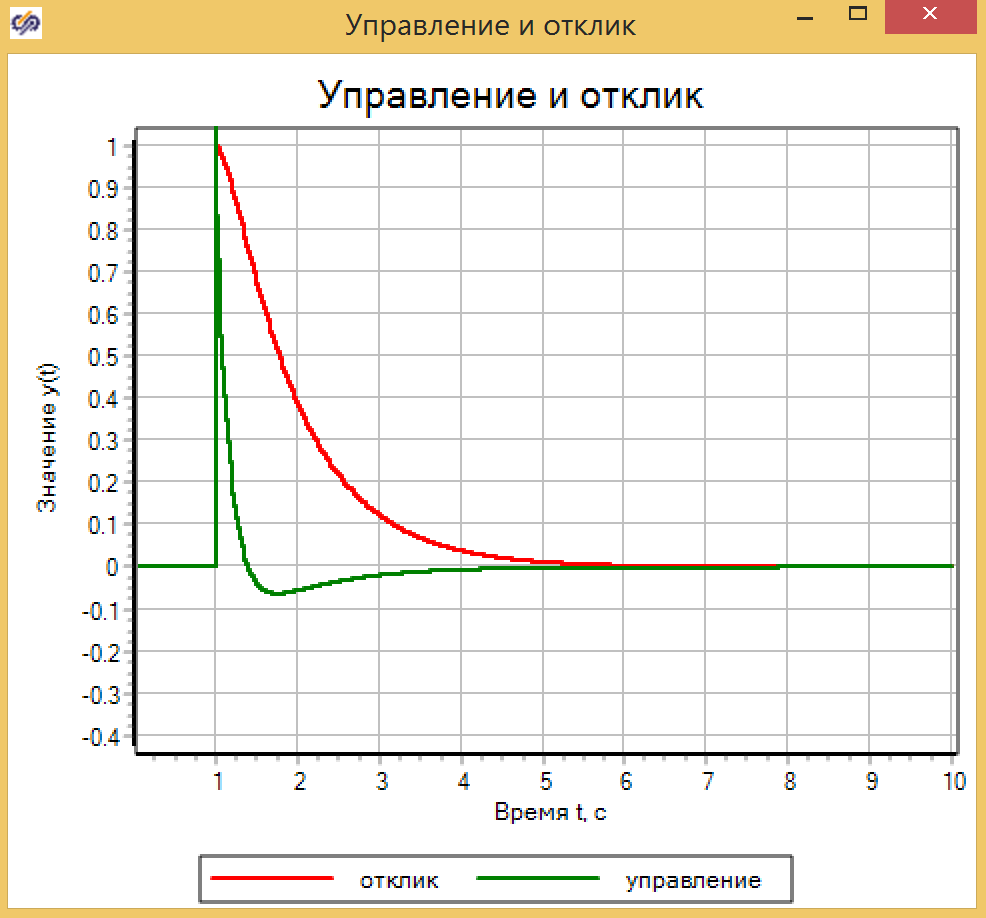
Рисунок 19. ПД-регулятор с единичными настройками.
В качестве оценки времени переходного процесса возьмем время, когда управляемая величина отклоняется от заданной менее чем на 0.009. В этом случае получаются следующие результаты:
ПИД – 11.25 сек.
ПД — 5.25 сек.
FL – 4.74 сек.
Настройка регулятора FL с помощью блока оптимизации
Для настройки используем ту же самую схему, что и для настройки ПИД-регулятора (см. рис 6). Только рассчитывать и записывать в сигналы проекта мы будем параметры фазификации:
— uMax_1 – максимальное значение выхода регулятора;
— deltaMax_1 – максимальное отклонение;
— divMax_1 – максимальная производная.
На старте у нас все эти параметры равны 1. После запуска процесса автоматизации в них будут рассчитаны оптимизированные значения.
В блоке оптимизации используются стохастические методы, поэтому есть смысл выполнить несколько последовательных запусков расчетов оптимизации для достижения наилучших результатов.
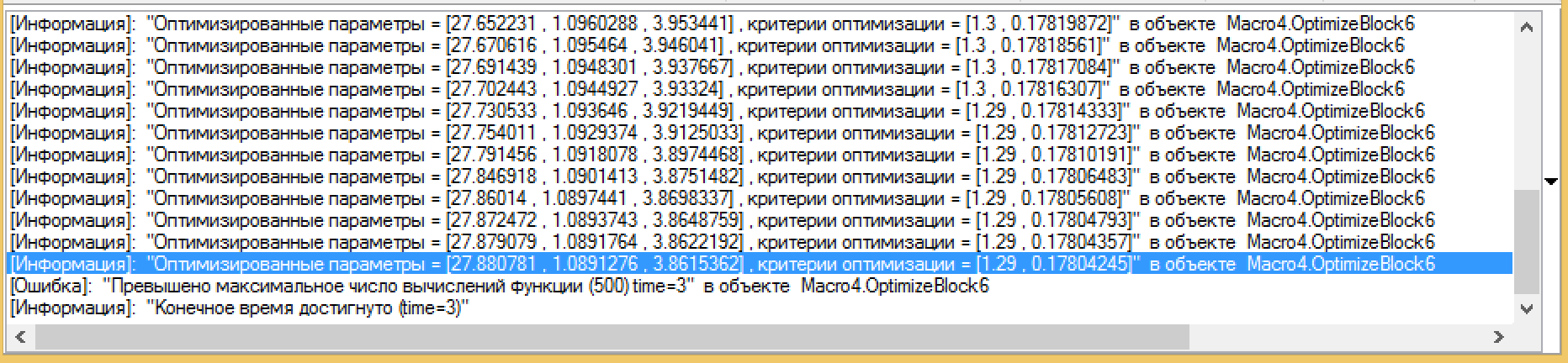
Рисунок 20. Сообщения о результатах работы блока оптимизации.
Например, когда появляется ошибка по сходимости или превышается количество вычислений функции, можно в качестве исходного приближения взять рассчитанные из предыдущего прогона оптимизации.
Для этого в параметрах блока оптимизации в качестве начальных приближений блока нужно указать сигналы проекта. Тогда в процессе расчета при повторном запуске в качестве исходных данных будут браться результаты предыдущей оптимизации.

Рисунок 21. Параметры блока оптимизации.
С первого прогона получилось оптимизировать время переходного процесса до 0.24
[Информация]: «Оптимизированные параметры = [31.10359, 1.0219553, 2.165446], критерии оптимизации = [1.24, 0.09879439]» в объекте Macro4.OptimizeBlock6
Второй прогон процесса оптимизации сократил время переходного процесса до 0.23 сек.
[Информация]: «Оптимизированные параметры = [34.954824, 1.0114662, 0.058949452], критерии оптимизации = [1.23, 0.098544697]» в объекте Macro4.OptimizeBlock6
Переходной процесс для ПИД и FL представлен на рисунке 22. Видно, что нечеткий регулятор справляется быстрее ПИД.
 ПИД регулятор |
 FL регулятор |
| Рисунок 22. Переходной процесс при ПД и FL регуляторов. | |
Конечные автоматы для переключения между регуляторами
Для переключения между двумя регуляторами можно использовать простой ключ, который переключает выход между двумя работающим регуляторами.
Но мы не ищем легких путей, мы используем конечные автоматы. Одним из преимуществ конечных автоматов является экономия вычислительных ресурсов. В схемах с переключателем мы всегда имеем два работающих регулятора, один из которых управляет, другой просто выполняет никому не нужные вычисления, а переключатель выбирает результат какого регулятора использовать.
Если же поместить регулятор в блок состояния конечного автомата, то он будет работать, только когда состояние активно, а в неактивном состояния вычислений не будет.
Заменим наш регулятор на карту состояний. Карта состояний – это такой же блок субмодели SimInTech, который может содержать стандартные входы-выходы и и стандартные блоки схемы, но кроме этого содержит в себе машину для переключения состояний.
Заменяем блок нечеткой логики на карту состояний. Внутри карты состояния добавляем вход и выход и два состояния. Одно – для работы на больших скачках быстрого регулятора FL1, второе — для точной настройки FL2. Выглядеть схема будет примерно так, как показано на рисунке 23:
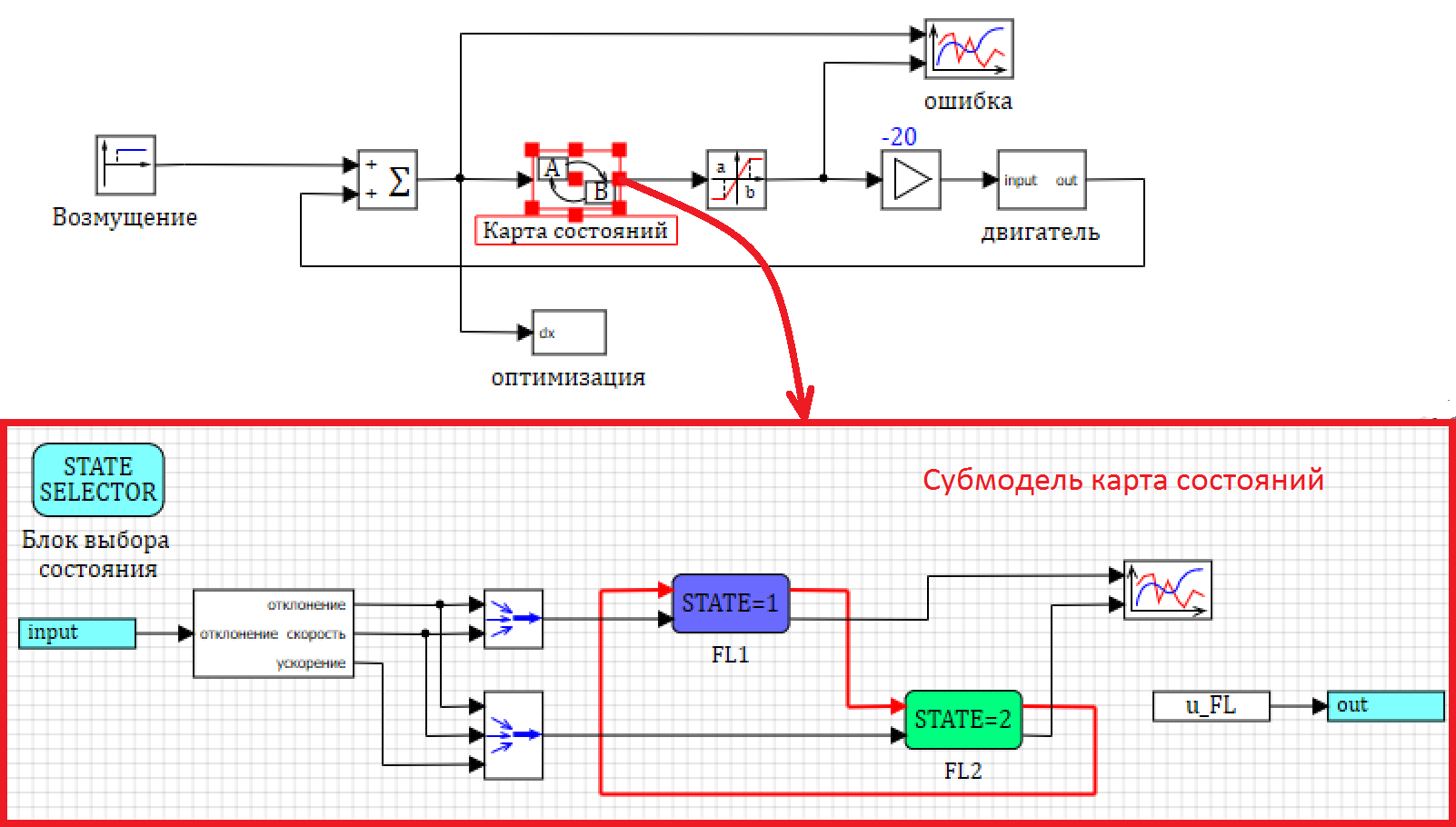
Рисунок 23. Сообщения о результатах работы блока оптимизации.
Потенциальные ошибки при использовании конечных автоматов
При использовании конечных автоматов нужно помнить, что хотя они являются такими же блоками как и другие субмодели, и в них можно выполнять любые вычисления и добавлять любые входы – выходы, их работа в модели существенно отличается.
Обратите внимание, что блок расчета скорости изменений и второй производной скорости изменений вынесен из блоков состояний.
Причина в том, что если вычислять производные разностной схемой, то в момент переключения между состояниями расчёт производных будет неверным, поскольку задержка на шаг интегрирования будет содержать не предыдущее по времени значение, а запомненное на момент выключения блока. То же самое относится к интеграторам.
Чтобы оценить, какая при этом будет ошибка, я собрал простую схему конечных автоматов, работающих по таймеру с переключением «1 секунда», в один из которых поместил субмодель расчёта скорости и ускорения разностными методами, период дискретизации 0.001 сек (постоянный шаг интегрирования). Такой же блок оставил вне конечных автоматов. Входное воздействие — линейное нарастание сигнала.
Сигнал, приходя через блок состояния, в период когда само состояние выключено, не меняется (морозится), и появляются ступеньки. А вот значение скорости, рассчитываемое в блоке состояния в момент переключения, увеличивается в 1000 раз, а ускорение вообще в 1 000 000 раз. см. рис. 24.
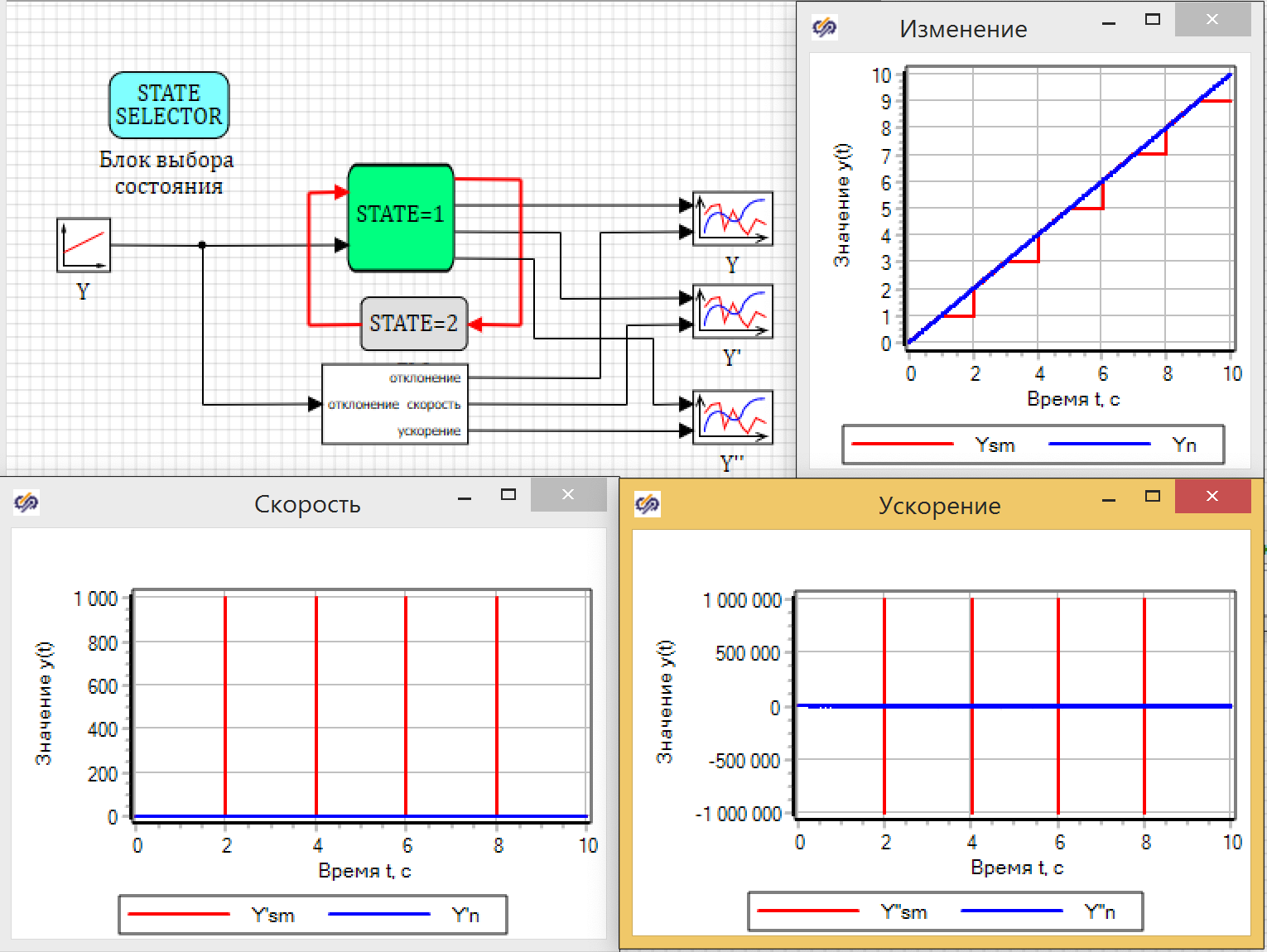
Рисунок 24. Ошибки вычисления скорости и ускорения разностными методами.
Начинка блоков состояния конечного автомата
Тут все достаточно просто: на вход поступает вектор отклонения скорости отклонения и ускорения отклонения, из этого вектора берется отклонение и сравнивается с константой 0.009. Если модуль отклонения меньше или равно, значит этот регулятор не работает, и осуществляем переход на второе состояние.
Вектор также подается в нечеткий регулятор FL1, которые мы настроили на предыдущем этапе. Результат рассчитанный в регуляторе, записывается в сигнал проекта u_FL. Понятно, что такая запись происходит, только когда состояние активно.

Рисунок 25. Модель состояния 1.
Для состояния два – все то же самое, только переход в состояние 1 осуществляется, если модуль отклонения больше 0.009.
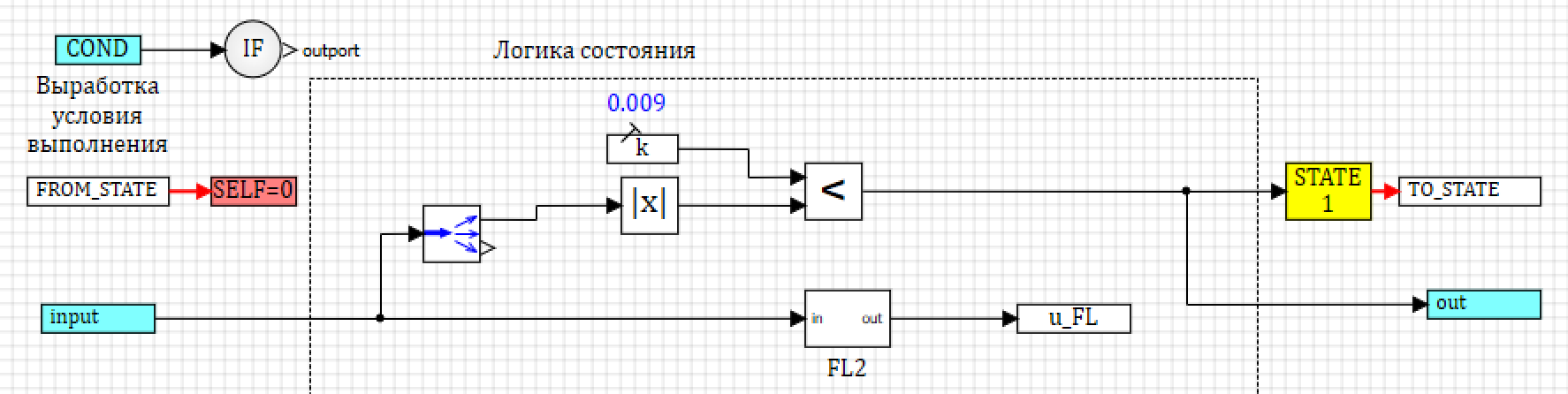
Рисунок 26. Модель состояния 2.
В качестве точного регулятора используем регулятор по отклонению первой и второй производной отклонения (именно такие регуляторы использует в своей книге В.И. Гостев и их мы использовали в предыдущих задачах). Схема регулятора представлена на рисунке 24.
В произвольный момент времени у нас активно либо первое либо второе состояние, соответственно, запись сигнала регулирующего воздействия u_FL идет либо с первого FL1, либо со второго FL2 нечеткого регулятора.
Нечеткий регулятор точной настройки
Рассмотрим второй нечеткий регулятор. Будем использовать регулятор, рекомендованный в книге. Данный регулятор в качестве входных величин получает отклонение, скорость изменения и ускорения изменения. Каждая из переменных, поступающая в регулятор с помощью блока фазификации, разбивается на три терма.
Отклонение – больше, норма, меньше.
Скорость изменения – растет, не изменяется, падает.
Ускорение изменения — ускоряется, не изменяется, замедляется.
Логические правила так же просты и незатейливы, как в предыдущих примерах:
1) если отклонение больше и скорость изменения растет и ускорение изменения ускоряется, то воздействие уменьшать.
2) если отклонение в норме и скорость изменения постоянна и ускорение изменения не изменяется, то воздействие не изменять.
3) если отклонение меньше и скорость изменения падает и ускорение изменения замедляется, то воздействие увеличивать.
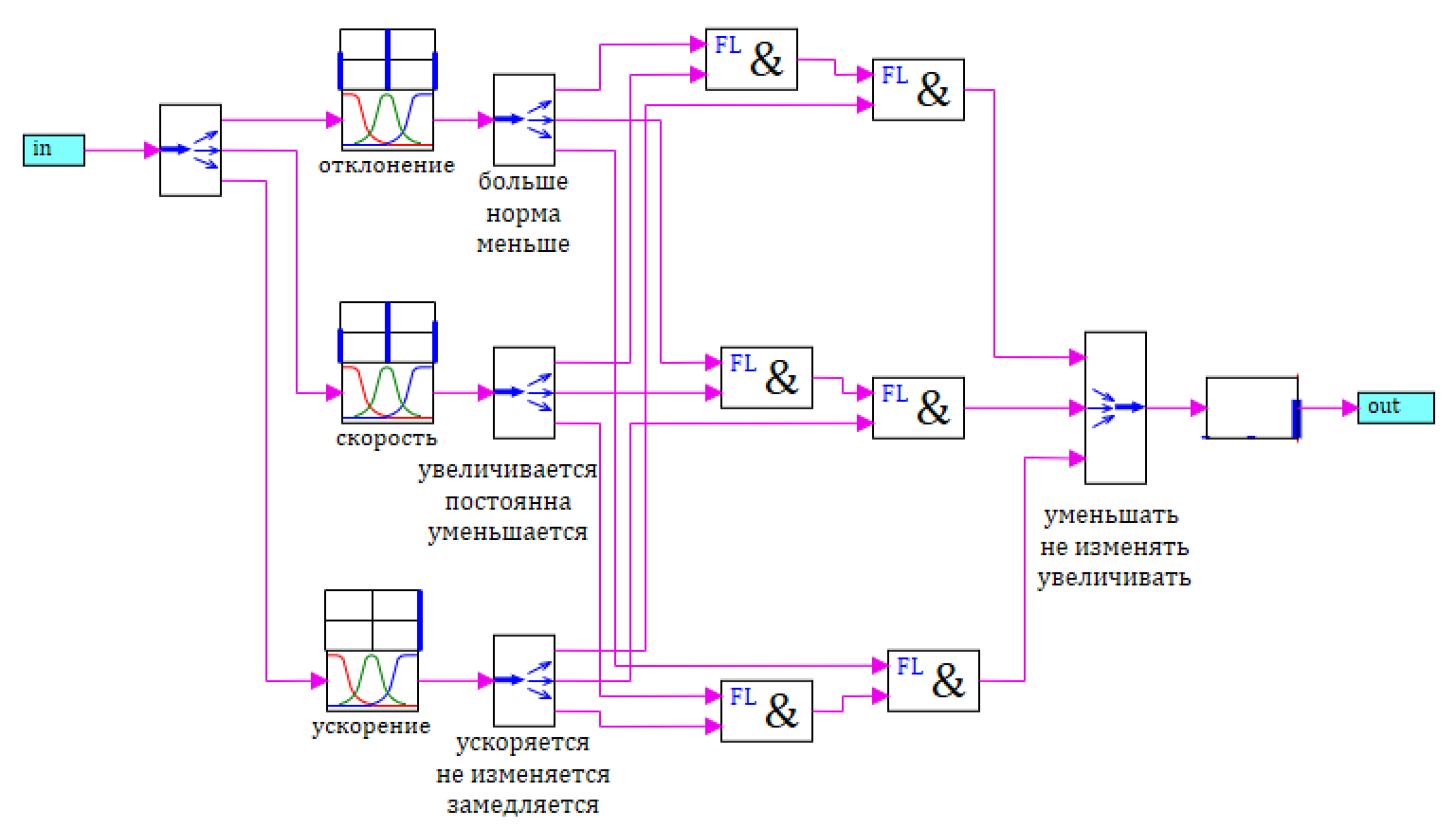
Рисунок 27. Нечеткий регулятор точной настройки FL2.
Nже как для первого регулятора, чтобы сократить количество настраиваемых переменных, принимаем диапазон изменения входных переменных и выхода регулятора симметричный относительно 0, тогда достаточно одного числа для задания диапазона фазификации.
Для настройки такого регулятора нам необходимо определить уже четыре числа:
— uMax_2 – максимальное значение выхода регулятора;
— deltaMax_2 – максимальное отклонение;
— divMax_2 – максимальная скорость;
— div2Max_2 – максимальное ускорение.
Добавляем их в список сигналов проекта и задаем значения по умолчанию 1 (см. рис. 28)
Запуск данной системы с 1 настройками показал, что все-таки чудес не бывает, и то, что наш нечеткий регулятор 1 с единичными настройками смог стабилизировать систему (см. рис. 18 — 19) – это скорее исключение, чем правило. Потому что результат работы регулятора представляет собой сплошную пилу включения и выключения. (см. рис. 28)

Рисунок 28. Результаты работы нечёткого регулятора с начальными настройками.
Настройка второго нечеткого регулятора
Первый вариант оптимизации: поскольку у нас переходный процесс уже завершился, в качестве критерия оптимизации используем среднеквадратичное отклонение. Схема оптимизации представлена на рисунке 29, результат – на рисунке 30.
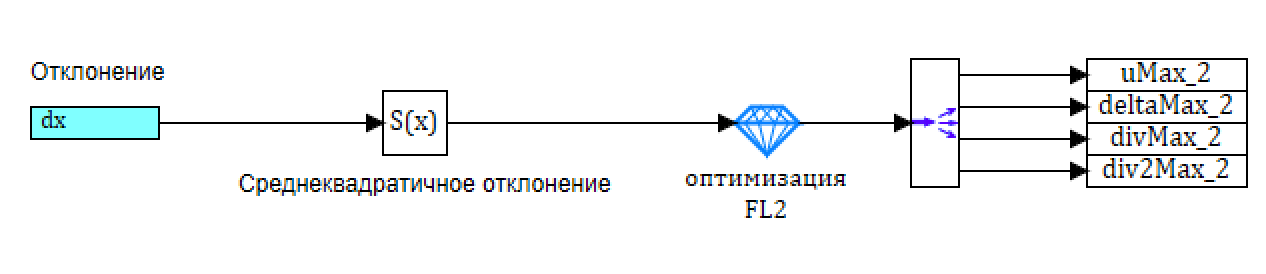
Рисунок 29. Схема оптимизации по отклонению.

Рисунок 30. Результат работы оптимизированного по отклонению регулятора.
Результат явно не тот, который мы ожидали. Регулятор для оптимизации отклонения работает, не останавливаясь ни на секунду. Соответственно, мы должны в критерий оптимизации включить количество переключений.
Изменяем схему, добавив в критерии автоматизации счетчик количества переключений. Для этого добавляем в качестве входа регулирующее воздействие.
Счетчик работает следующим образом:
Регулирующее воздействие подается в блок sign, который выдает -1,0,1 при смене знака воздействия, а после ставится блок «импульс по фронту», который выдает импульс длительностью в 1 шаг интегрирования. В момент когда происходит смена знака, после него стоит интегратор, который накапливает эти импульсы.
Накопленное количество переключений предаем в блок оптимизации, который пытается его минимизировать вместе с отклонениями.
Кроме этого, среднеквадратичное отклонение в процессе оптимизации начинаем считать, не сначала процесса с 1.2 секунды, для этого на вход установлен временной ключ.
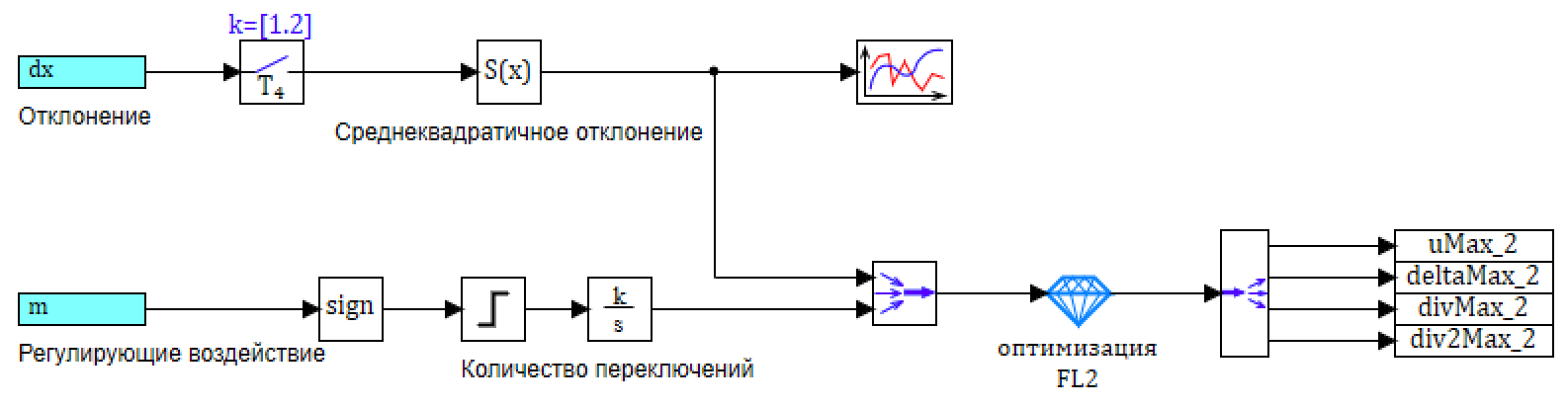
Рисунок 31. Схема оптимизации с учетом пeрeключений.
Такая оптимизация приводит к следующему результату:
[Информация]: «Оптимизированные параметры = [16.564415, 0.0027674129, 0.19085771, 50], критерии оптимизации = [0.0047956855, 11]» в объекте Macro5.OptimizeBlock6
Это значит, что:
— uMax_2 – максимальное значение выхода регулятора = 16.564;
— deltaMax_2 – максимальное отклонение = 0.00277;
— divMax_2 – максимальная скорость = 0.191;
— div2Max_2 – максимальное ускорение = 50.
Переходной процесс при настроенном регуляторе приведен на рисунке 32.
 |
 |
| Рисунок 32. Переходной процесс при ПД и FL регуляторов. | |
Двойной ПИД регулятор
Ну, и чтобы сравнение было полным, создадим систему управления с конечными автоматами, в которых переключение осуществляется между двумя регуляторами ПИД. ПИД1, для быстрого регулирования при больши отклонениях и ПИД2 для тонкого регулирования, при малых отклонениях.
Внутренняя структура блока конечных автоматов представлена на рисунке 33. Как было показано ранее, расчет интегральной и дифференциальной составляющих выполняем вне блоков состояний, для избежания ошибки.
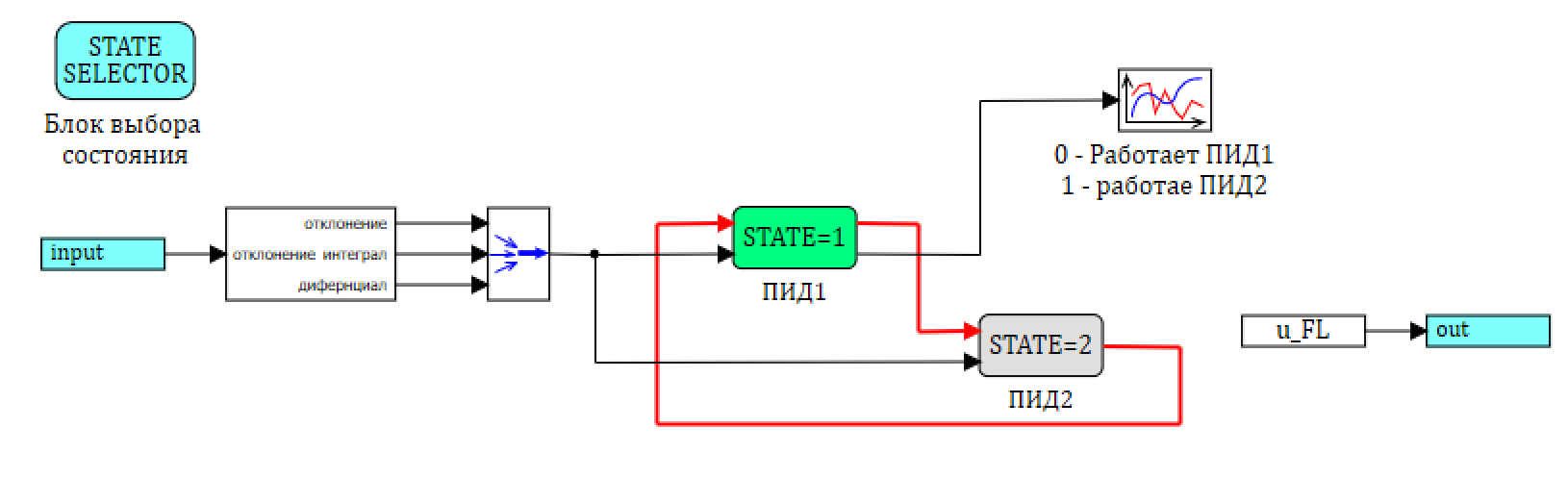 Рисунок 33. Блок конечных автоматов с переключениями ПИД1 и ПИД2.
Рисунок 33. Блок конечных автоматов с переключениями ПИД1 и ПИД2.
Внутри блока состояний вычисляется регулирующее воздействие путем сложения отклонения, интеграла и дифференциала с соответствующими коэффициентами, вычисленными в результате оптимизационного расчета, см. рис. 34.
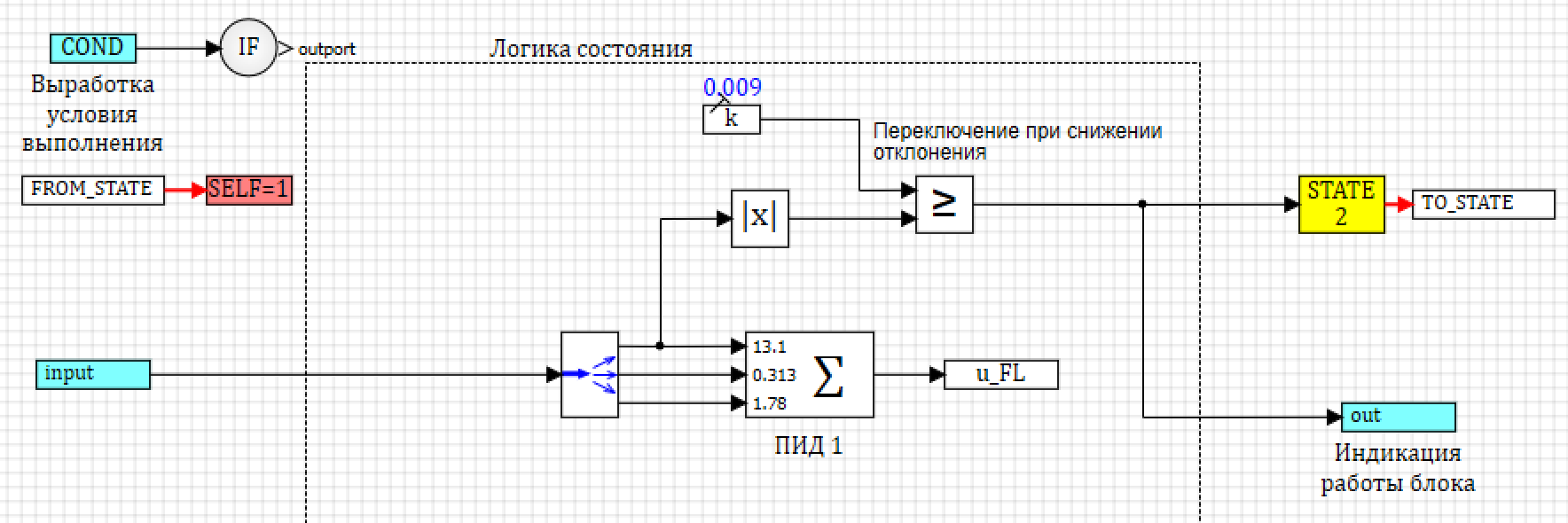
Рисунок 34. Состояние конечного автомата с вычислением ПИД-регулятора.
Настройку регулятора ПИД 2, осуществим аналогично настройки нечетких регуляторов, методом оптимизации по среднеквадратичному отклонению. Результаты работы настроенных ПИД-регуляторов с переключениями в конечных автоматах:
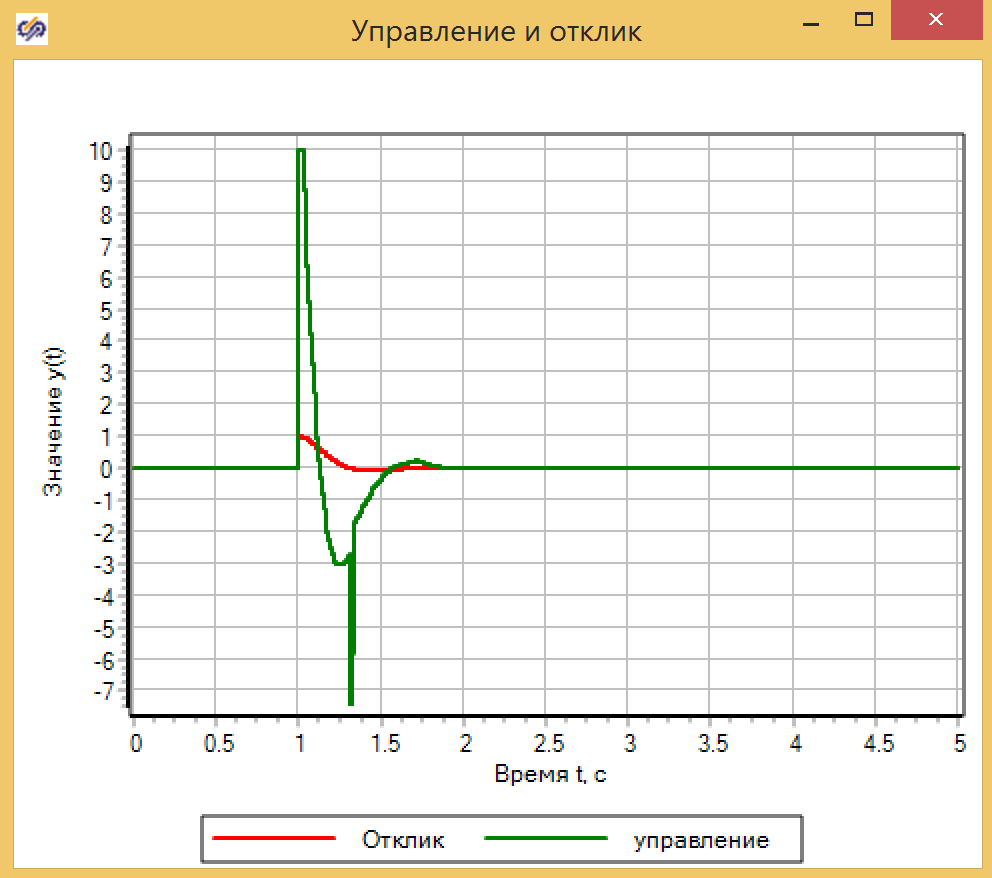
Рисунок 35. Переходной процесс с ПИД-регуляторами.
Сравнение результатов оптимизированного расчёта с переключением ПИД и Нечеткой логики приведено в таблице:
| Регуляторы | Время переходного процесса | Конечное отклонение |
| FL | 1.26 сек | -6.35938146587023E-9 |
| ПИД | 1.71 сек. | -2.40475404943874Е-4 |
Выводы
Для данной модели двухроторного газотурбинного двигателя управление регулятор на базе нечеткой логики, показало лучшее результат, чем ПИД регулятор.
Взять проекты из статьи для самостоятельного изучения можно здесь...