В приложении к статье путь частицы предоставлены вырезанные материалы: интегралы по траекториям, двухщелевой эксперимент на холодных атомах неона, кадры телепортации частиц и прочие сцены жестокости и сексуального характера.
По моему мнению, не может быть другого способа считать логически непротиворечивым математический формализм, чем демонстрация отклонения его следствий от опыта или доказательство того, что его предсказания не исчерпывают возможности наблюдений.
Нильс Бор
В заключение автор хотел бы заявить, что мы признаем только две веские причины для отказа от теории, объясняющей широкий спектр явлений. Во-первых, теория не является внутренне последовательной, а во-вторых, она не согласуется с экспериментами.
Дэвид Бом
Ранее мы узнали, откуда берется уравнение Шредингера, для чего оно оттуда берется, и как оно берется различными методами
Теперь, разобьем-ка его на два вещественных уравнения. Для этого представим пси в полярной форме , подставим его в исходную формулу и запишем отдельно вещественную и мнимую части:
S — есть квантовый аналог действия, а квадрат R — плотность вероятности. Второе уравнение, значится, говорит нам о непрерывности сжиженной вероятности, а первое — это всего лишь уравнение Гамильтона-Якоби, с квантовым потенциалом (третье слагаемое).
Если внимательно присмотреться к уравнению непрерывности и вспомнить гидродинамику, то можно выудить скорость . Так, S у нас фаза пси-функции, ну и по-хорошему надо ее через эту пси-функцию выразить:
Таким образом, если у нас есть пси-функция, полученная, скажем, при решении уравнения Шрёдингера или интегралов по траекториям, то можно вывести функцию S, продифференцировать ее, что даст явно скорость частицы, а зная скорость, легко получить координату. Собственно, вот и вся бомовская механика, дальше уже дело техники. Так что приступим-с.
Туннельный эффект
Туннелирование — это явление прохождения частицей сквозь область пространства, пребывание в которой запрещено классической механикой. В более общем случае, этот эффект проявляется в преодолении системой потенциального барьера, при том, что ее полная энергия меньше этого самого барьера. Это может быть и автоэлектронная эмиссия, и прохождение заряда через диэлектрическую пленку, и начало химической реакции еще до того, как молекулы пристроились друг к другу своими реакционными центрами.
Касательно классических аналогий натыкался на пример, где звонко прыгающий по залу баскетбольный мяч натыкается на мат, на котором скачки экспоненциально затухают, после чего мяч скачет не так задорно. Или еще прохождение предмета сквозь стену. Но эти примеры скорее про диссипацию и про особенности теории вероятности. Как правило, привычные образы из классики только запутывают, но может у кого что и выйдет, так что предлагаю устроить в комментах конкурс на самый лучший пример туннелирования.
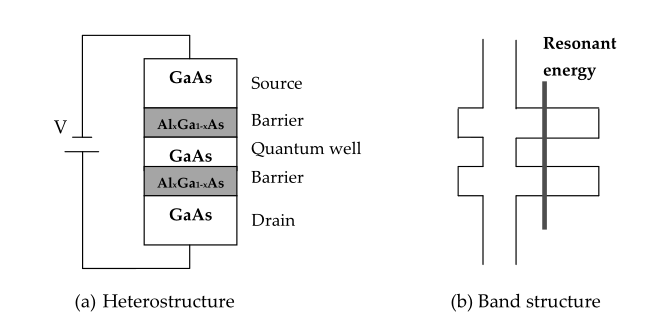
Две статьи назад поднималась мысль, что стационарное уравнение Шредингера вполне решаемо аналитически для многослойных сред.
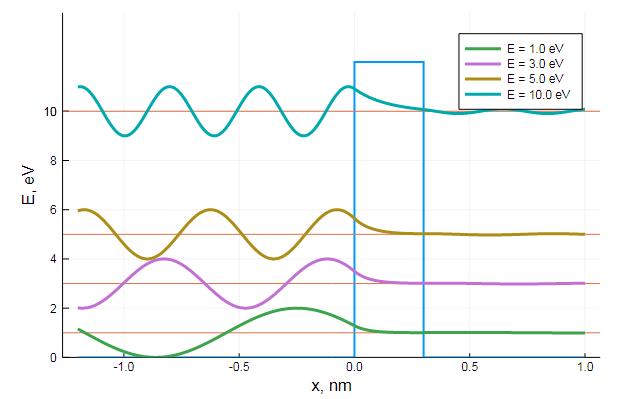
Согласно представленной выше конфигурации системы, для того, чтобы преодолеть злосчастные три ангстрема, частице нужно иметь в пороховнице минимум дюжину электронвольт. Но как видно, уже на десяти происходит просачивание (да и на пяти какие-то околонулевые колебания). Но самая магия начинается при увеличении количества слоев:
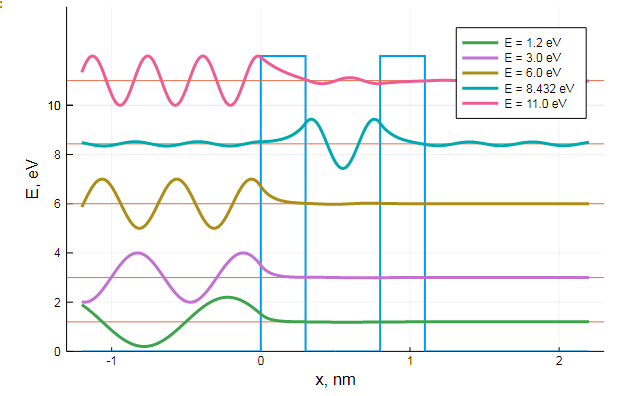
При особых энергиях (резонансных) переход через два барьера происходит без каких либо видимых изменений для волночастицы
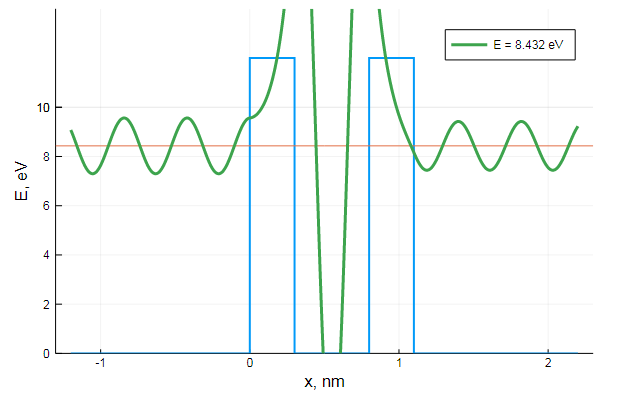
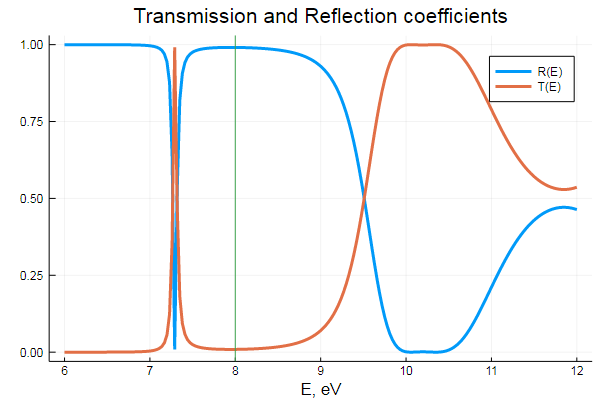
Разумеется, резонансов может быть и больше, к тому же, они точно также работают и в обратную сторону: то есть, у частицы с энергией превышающей барьер есть все шансы отразиться обратно
Это все обычная волновая механика, но хотелось бы глянуть на частицы. Численно решать временное уравнение Шредингера мы умеем. А с эволюцией волновой функции несложно получить динамику для частиц. Скорость частицы определяется как
Производную не составит труда найти конечными разностями на пси-сетке, а потом уже обновлять координату некоторой частицы:
using LinearAlgebra, SparseArrays, Plots
const ħ = 1.0546e-34 # J*s
const m = 9.1094e-31 # kg
const q = 1.6022e-19 # Kl
const nm = 1e-9 # m
const fs = 1e-12; # s
function wavefun()
gauss(x) = exp( -(x-x0)^2 / (2*σ^2) + im*x*k )
k = m*v/ħ
# Гамильтониан как разреженная матрица
Vm = spdiagm(0 => V )
H = spdiagm(-1 => ones(Nx-1), 0 => -2ones(Nx), 1 => ones(Nx-1) )
H *= ħ^2 / ( 2m*dx^2 )
H += Vm
A = I + 0.5im*dt/ħ * H # Левая матрица
B = I - 0.5im*dt/ħ * H # Правая
psi = zeros(Complex, Nx, Nt)
psi[:,1] = gauss.(x)
for t = 1:Nt-1
b = B * psi[:,t]
# Использует встроенные солверы для решения СЛАУ A*psi = b
psi[:,t+1] = A \ b
end
return psi
enddx = 0.05nm # x step
dt = 0.01fs # t step
xlast = 400nm
Nt = 260 # Number of time steps
t = range(0, length = Nt, step = dt)
x = [0:dx:xlast;]
Nx = length(x) # Number of spatial steps
a1 = 200nm
a2 = 200.5nm # 1 Ангстрем
a3 = 205nm
a4 = 205.5nm
#V = [ a1<xi<a2 ? 2q : 0.0 for xi in x ] # 2 eV
V = [ a1<xi<a2 || a3<xi<a4 ? 2q : 0.0 for xi in x ] # 2 eV
x0 = 80nm # Initial position
σ = 20nm # gauss width
v = -120nm/fs;
@time Psi = wavefun()
P = abs2.(Psi);
function ψ(xi, j)
k = findfirst(el-> abs(el-xi)<dx, x)
k == nothing && ( k = 1 )
Psi[k, j]
end
function corpusculaz(n)
X = zeros(n, Nt)
X[:,1] = x0 .+ σ*randn(n)
for j in 2:Nt, i in 1:n
U = ħ/(2m*dx) * imag( ( ψ(X[i,j-1]+dx, j) - ψ(X[i,j-1]-dx, j) ) / ψ(X[i,j-1], j) )
X[i,j] = X[i,j-1] - U*dt
end
X
end
@time X = corpusculaz(20);
plot(x, P[:, 1], legend = false)
plot!(x, P[:, 80], legend = false)
scatter!( X[:,1], zeros(20) )
scatter!( X[:,80], zeros(20) )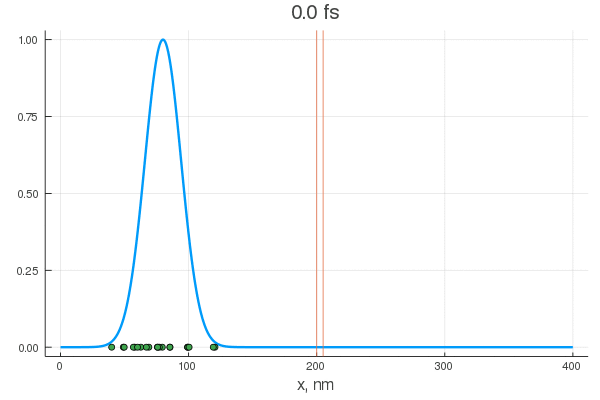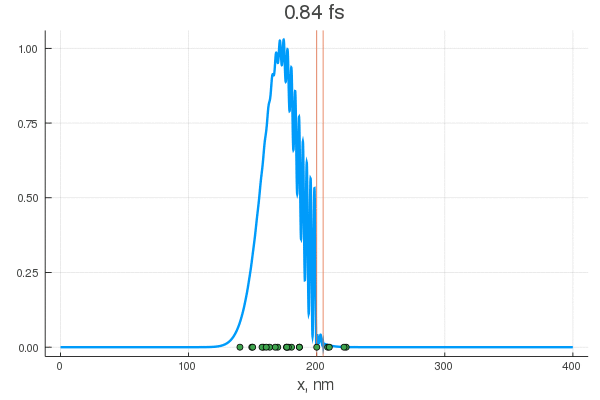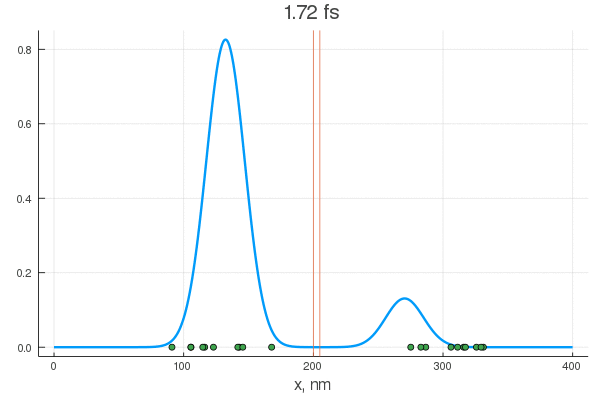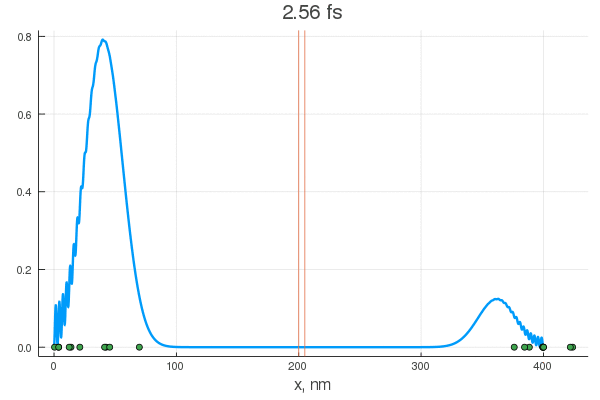
Уравнение описывает перекатывание горошинок с начальным нормальным распределением. Их тащит гауссов пакет — цуг волн разных частот, и у некоторых из них есть шанс проскочить. Для различных конфигураций получается интересное поведение:
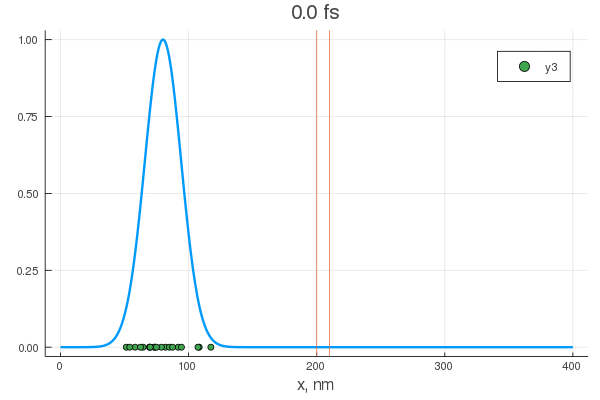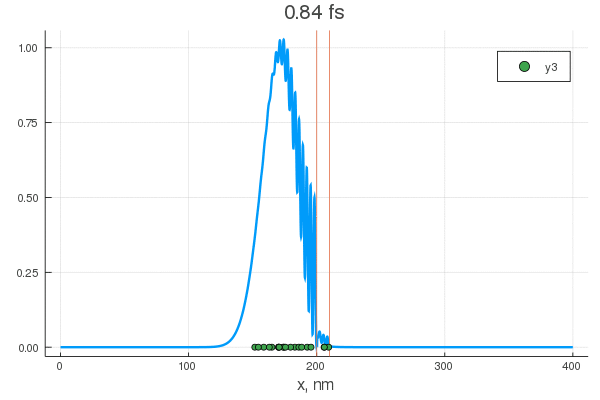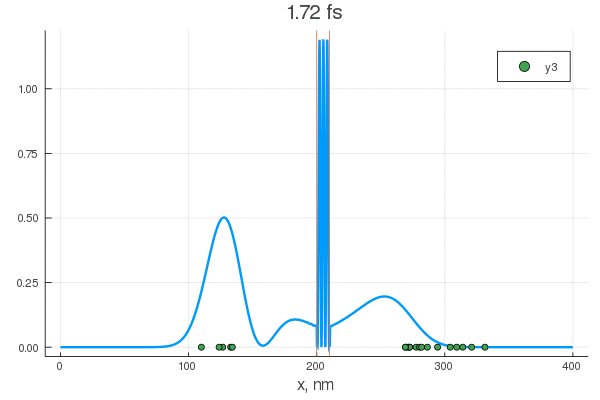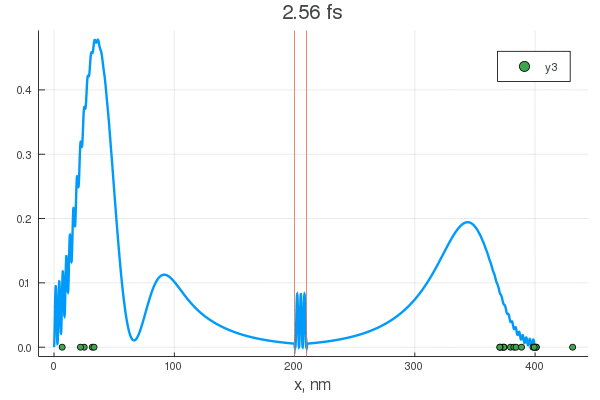
Теперь осталось подобрать нужные материалы, напылить их тонкими слоями и проверить численные предсказания. Дальше стоит посмотреть разные формы барьеров, оценить вероятность и время туннелирования и вперед, делать компьютеры на основе атомотроники!
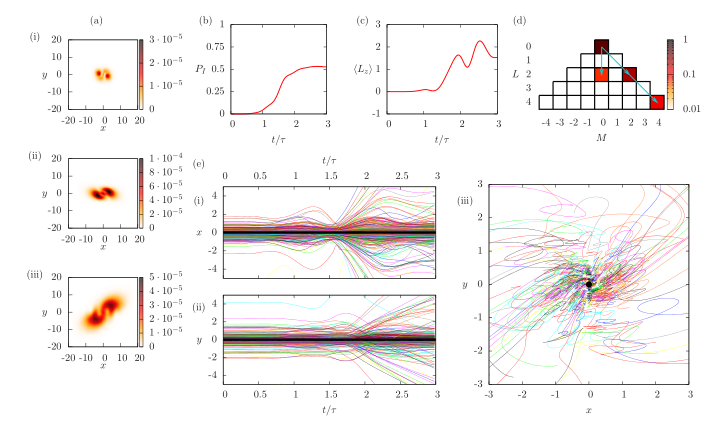
Двухщелевой эксперимент
Своей установки у нас нет, и в таких ситуациях обычно работают по результатам статей экспериментаторов. Double-slit interference with ultracold metastable neon atoms — здесь авторы собрали охлажденные атомы неона в магнито-оптическую ловушку. Потом это дело пуляется горизонтально вниз на двухаппертурный экран
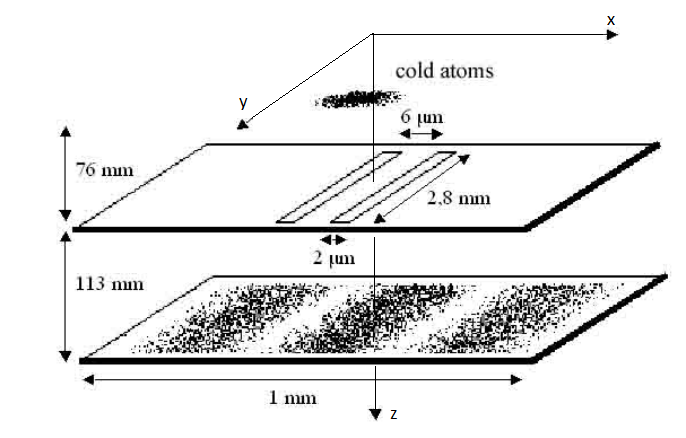
Зададим все параметры установки и стандартные отклонения для динамически величин
using Random, Gnuplot, Statistics
# для интегрирования
function trapez(f, a, b, n)
h = (b - a)/n
result = 0.5*(f(a) + f(b))
for i in 1:n-1
result += f(a + i*h)
end
result * h
end
# для дифуров
function rk4(f, x, y, h)
k1 = h * f(x , y )
k2 = h * f(x + 0.5h, y + 0.5k1)
k3 = h * f(x + 0.5h, y + 0.5k2)
k4 = h * f(x + h, y + k3)
return y + (k1 + 2*(k2 + k3) + k4)/6.0
endconst ħ = 1.055e-34 # J*s
const kB = 1.381e-23 # J*K-1
const g = 9.8 # m/s^2
const l1 = 76e-3 # m
const l2 = 113e-3 # m
const yh = 2.8e-3 # m
const d = 6e-6 # m
const b = 2e-6 # m
const a1 = 0.5(- d - b) # щели
const a2 = 0.5(- d + b)
const b1 = 0.5( d - b)
const b2 = 0.5( d + b)
const m = 3.349e-26 # kg
const T = 2.5e-3 # K
const σv = sqrt(kB*T/m) # разброс скорости
const σ₀ = 10e-6 # 10 mkm # разброс по х и по у
const σz = 3e-4 # 0.3 mm # по z
const σk = m*σv / (ħ*√3) # 2e8 m/s # отклонение для волнового вектора
v₀ = zeros(3)
k₀ = zeros(3);Стратегия такая: задача разбивается на две части, до и после щелей, и в каждом случае находится поведение пси-функции, а потом получаются траектории.
Предаппертурная волновая функция
Для каждого атома с начальным волновым вектором k волновая функция в начальный момент имеет вид
Ничего страшного, это просто распределение Гаусса в трех измерениях. Теперь бы узнать, как это распределение будет эволюционировать в нашей установке, да желательно, иметь аналитическое выражение. Те, кто достаточно глубоко изучал некоторые моменты квантовой механики, разумеется знают об интегралах по траекториям.
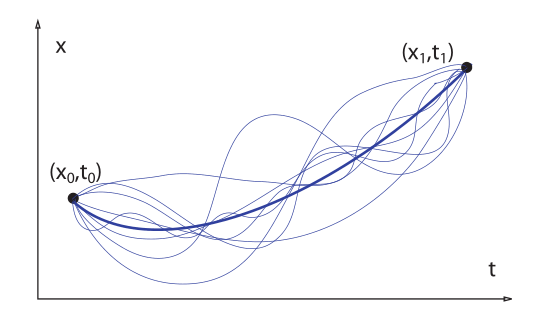
Согласно фейнмановскому формализму, вероятность перехода между двумя точками в фазовом пространстве вычисляется с использованием всех возможных путей между этими двумя точками. Но в отличие от механики Бома, где каждая квантовая частица следует определенной траектории детерминированным образом, фейнмановский подход — это лишь сумма по возможным историям. К слову, эту методику сначала было тоже приняли в штыки, дескать, опять вы со своими классическими путями. Но Фейнман убедил нудных нужных людей, что траектории виртуальные, и это просто удобный подход без замахов на философию.
Подробней с этой техникой можно ознакомиться в книге Quantum Mechanics And Path Integrals, A. R. Hibbs, R. P. Feynman, в частности, задачи пункта 3.6 это наш случай.
В двух словах, все возможные траектории между двумя точками образуют ядро
Ядро по Z отличается, потому как там добавляется сила тяжести. Как показал Фейнман, теперь можно находить волновую функцию в разных точках в разное время просто решая интеграл
Эти интегралы допускают разделение переменных, так что можно искать решение для каждой координаты отдельно. Так, нас в первую очередь интересует размерность по X, так как именно по ней будет просматриваться вся интерференция. Решаем интеграл в области до щели:
Итак, у нас есть плотность вероятности до щели:
ε₀(t) = σ₀^2 + ( ħ/(2m*σ₀) * t )^2 + (ħ*t*σv/m)^2
s₀(t) = σ₀ + im*ħ/(2m*σ₀) * t
ρₓ(x, t) = exp( -x^2 / (2ε₀(t)) ) / sqrt( 2π*ε₀(t) )
t₁(v, z) = sqrt( 2*(l1-z)/g + (v/g)^2 ) - v/g
tf1 = t₁(v₀[3], 0) # s # время достижения первого экрана
X1 = range(-100, stop = 100, length = 100)*1e-6
Z1 = range(0, stop = l1, length = 100)
Cron1 = range(0, stop = tf1, length = 100)
P1 = [ ρₓ(x, t) for t in Cron1, x in X1 ]
P1 /= maximum(P1); # нормируем на единицу
@gp "set title 'Wavefun before the slits'" xlab="Z, mkm" ylab="X, mkm"
@gp :- 1000Z1 1000000X1 P1 "w image notit"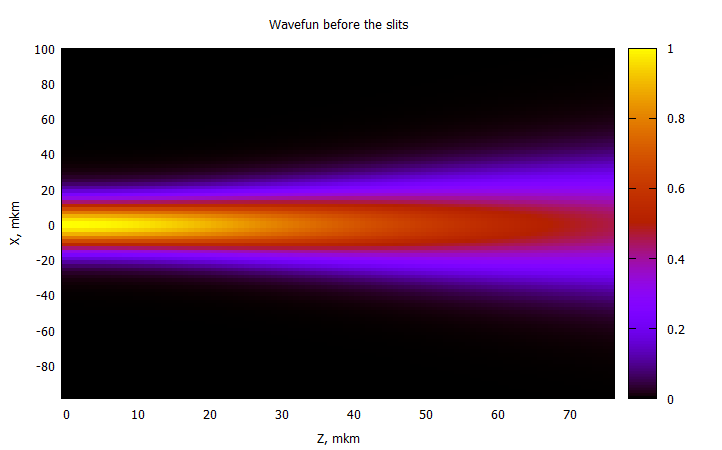
Расплывание пакета — пока ничего интересного.
Постаппертурная волновая функция
Далее будет веселее, так как теперь интегралы решаются для щелей:
А плотность вероятности тогда
Эту гадость уже не запуассонить, так что метод трапеций в помощь:
function ρₓ(xᵢ, tᵢ)
Kₓ(xb, tb, xa, ta) = sqrt( m/(2im*π*ħ*(tb-ta)) ) * exp( im*m*(xb-xa)^2 / (2ħ*(tb-ta)) )
function subintrho(k)
ψₓ(x, t) = ( 2π*s₀(t) )^-0.25 * exp( -(x-ħ*k*t/m)^2 / (4σ₀*s₀(t)) + im*k*(x-ħ*k*t/m) )
subintpsi(x) = Kₓ(xᵢ, tᵢ, x, tf1) * ψₓ(x, tf1)
ψa = trapez(subintpsi, a1, a2, 200)
ψb = trapez(subintpsi, b1, b2, 200)
exp( -k^2 / (2σv^2) ) * abs2(ψa + ψb)
end
trapez(subintrho, -10σk, 10σk, 20) / sqrt( 2π*σv^2 )
endt₂(v, z) = sqrt( 2*(l1+l2-z)/g + (v/g)^2 ) - v/g
tf2 = t₂(v₀[3], 0) # s # время достижения второго экрана
X2 = range(-800, stop = 800, length = 200)*1e-6
Z2 = range(l1, stop = l2, length = 100)
Cron2 = range(tf1, stop = tf2, length = 100)
@time P2 = [ ρₓ(x, t) for t in Cron2, x in X2 ];
P2 /= maximum(P2[4:end,:]);
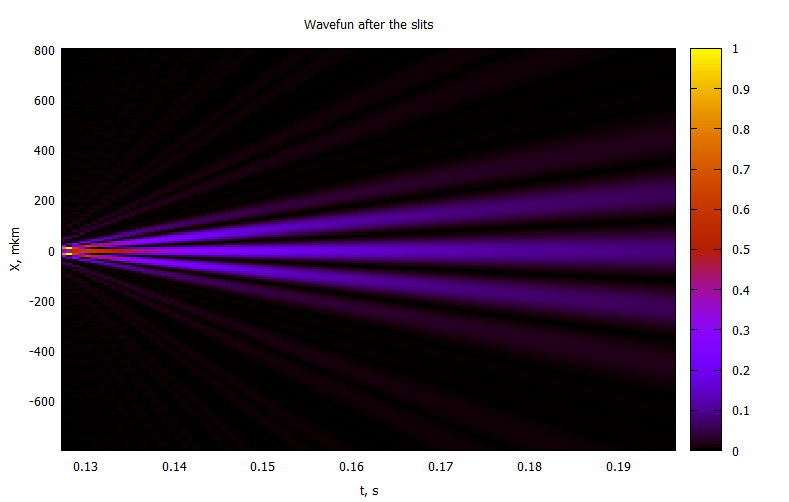
@gp "set title 'Wavefun after the slits'" xlab="t, s" ylab="X, mkm"
@gp :- Cron2[4:end] 1000000X2 P2[4:end,:] "w image notit"Для первых 2мм после щелей:
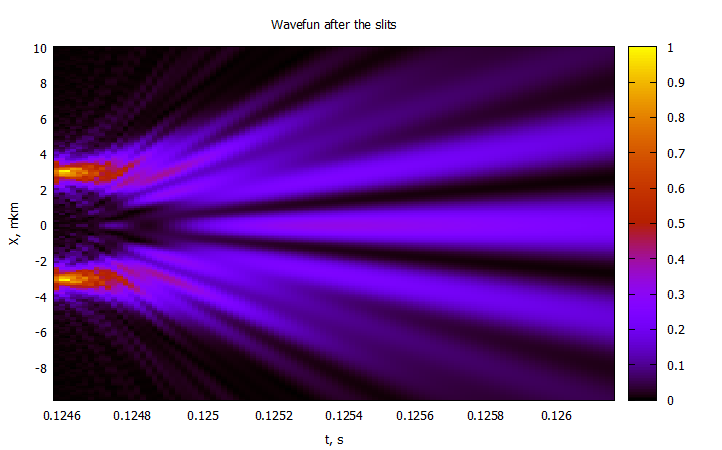
и до экрана
Траектории до щелей
Как помнится скорость находится по формуле:
Но для частиц со спинами такое не пройдет. По крайней мере до щелей вклад существенен. В таких ситуациях решают уравнение Дирака, с которым подход Бома тоже вполне уживается, что дает немножко модифицированную формулу скорости
Ну а дальше, утирая слёзы радости и восторга, интегрируем
function xbs(t, xo, yo, vo)
cosϕ = xo / sqrt( xo^2 + yo^2 )
sinϕ = yo / sqrt( xo^2 + yo^2 )
atnx = -ħ*t / (2m*σ₀^2)
sinatnx = atnx / sqrt( atnx^2 + 1)
cosatnx = 1 / sqrt( atnx^2 + 1)
cosϕt = cosϕ * cosatnx - sinϕ * sinatnx
#sinϕt = sinϕ*cosatnx + cosϕ*sinatnx
σ₀t = sqrt( σ₀^2 + ( ħ*t / (2*m*σ₀) )^2 )
vo*t + sqrt(xo^2 + yo^2) * σ₀t/σ₀ * cosϕt
end
@gp "set title 'Trajectories before slits'" xlab="t, s" ylab="X, mkm" # "set yrange [-10:10]"
@time for i in 1:80
x0 = randn()*σ₀
y0 = randn()*σ₀
v0 = randn()*σv*1e-4
prtclᵢ = [ xbs(t,x0,y0,v0) for t in Cron1 ]
@gp :- Cron1 1000000prtclᵢ "with lines notit lw 2 lc rgb 'black'"
# slits -4-> -2, 2->4 mkm
end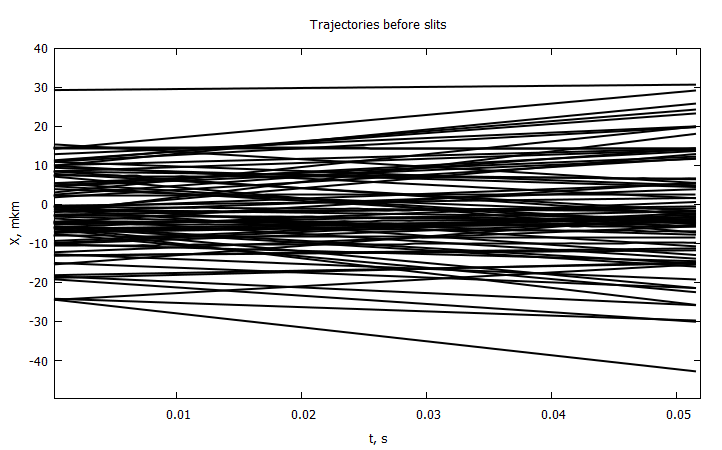
Стоит понимать, что частицы с существенной горизонтальной компонентой скорости будут разлетаться по большой площади, так что, для экономии вычислительного времени, можно отсортировывать нужные частицы с маленькими иксовыми скоростями, что будет давать больше корпускул попадающих в щель. Потом их координаты можно запомнить и использовать в следующей части эксперимента. А можно не использовать. Скажем, генерировать частицы равномерно или рандомно сразу на щелях.
Траектории после щелей
По направлению Y щели длинные, почти что даже бесконечные, поэтому движение вдоль этой координаты можно считать по старой формуле. А вот по X корпускулы должны двигаться уже в соответствии с интерференционной картиной задаваемой плотностью вероятности. При расчете скоростей после аппертурного экрана забудем о несущественном вкладе спинов.
Шутить про "в результате несложных преобразований" не буду, так как получение формулы то еще бумагомарание
function Uₓ(t, x)
γ = -m*x / ( ħ*(t-tf1) )
β = m/(2ħ) * ( 1/(t-tf1) + 1 / ( tf1*( 1 + (2m*σ₀^2 / (ħ*tf1) )^2 ) ) )
α = -( 4σ₀^2 * ( 1 + ( ħ*tf1 / (2m*σ₀^2) )^2 ) )^-1
f(x, u, t) = exp( ( α + im*β )*u^2 + im*γ*u )
C = f(x, a2, t) - f(x, a1, t) + f(x, b2, t) - f(x, b1, t)
H = trapez( u-> f(x, u, t) , a1, a2, 400) + trapez( u-> f(x, u, t) , b1, b2, 400)
return 1/(t-tf1) * ( x - 0.5/(α^2 + β^2) * ( β*imag(C/H) + α*real(C/H) - β*γ ) )
end
init() = bitrand()[1] ? rand()*(b2 - b1) + b1 : rand()*(a2 - a1) + a1
myrng(a, b, N) = collect( range(a, stop = b, length = N ÷ 2) )
n = 1
xx = 0
ξ = 1e-5
while xx < Cron2[end]-Cron2[1]
n+=1
xx += (ξ*n)^2
end
n
steps = [ (ξ*i)^2 for i in 1:n1 ]
Cronadapt = accumulate(+, steps, init = Cron2[1] )
function modelsolver(Np = 10, Nt = 100)
#xo = [ init() for i = 1:Np ] # случайные
xo = vcat( myrng(a2, a1, Np), myrng(b1, b2, Np) ) # равномерно
xpath = zeros(Nt, Np)
xpath[1,:] = xo
for i in 2:Nt, j in 1:Np
xpath[i,j] = rk4(Uₓ, Cronadapt[i], xpath[i-1,j], steps[i] )
end
xpath
end@time paths = modelsolver(20, n);
@gp "set title 'Trajectories after the slits'" xlab="t, s" ylab="X, mkm" "set yrange [-800:800]"
for i in 1:size(paths, 2)
@gp :- Cronadapt 1e6paths[:,i] "with lines notit lw 1 lc rgb 'black'"
endЭто благолепие решается методом Рунгу-Кутты 4 с переменным шагом, так как сразу после щелей плотность сетки играет существенную роль. Первые 2мм выходит такая картина
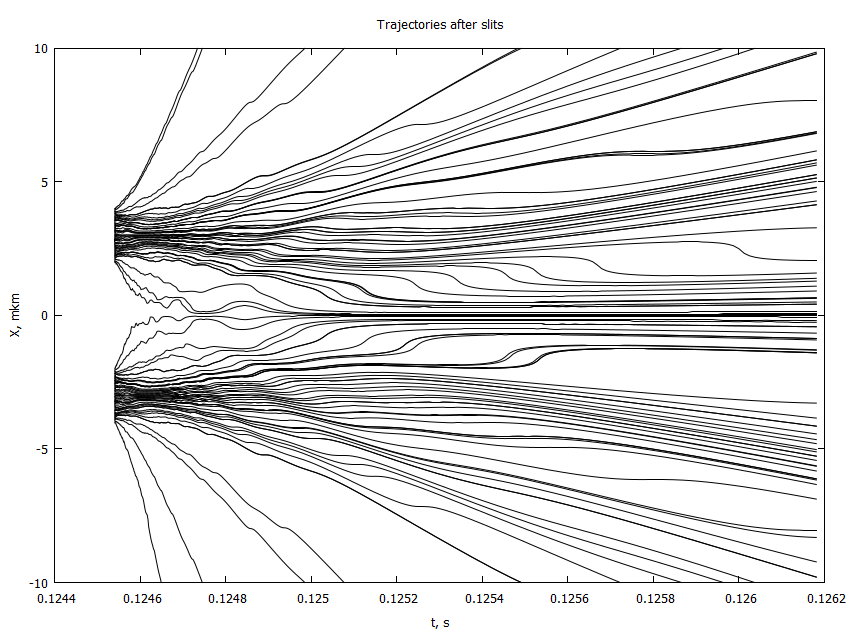
Заметьте, траектории не пересекаются: так как задача одномерная, пересечение будет равносильно совпадению частиц в пространстве, а онтологические детерминированные теории не допускают такого рода неопределенности. Ну и дорисуем до второго экрана
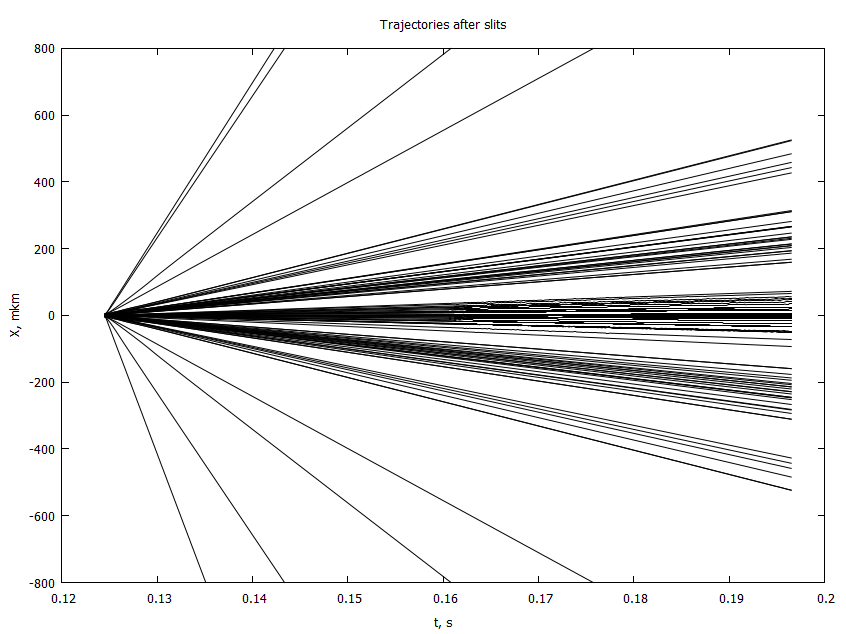
Результат вполне согласуется с распределением плотности вероятности. Собственно, глянем, что у нас выходит на экране
function yas(t, xo, yo, vo)
cosϕ = xo / sqrt( xo^2 + yo^2 )
sinϕ = yo / sqrt( xo^2 + yo^2 )
atnx = -ħ*t / (2m*σ₀^2)
sinatnx = atnx / sqrt( atnx^2 + 1)
cosatnx = 1 / sqrt( atnx^2 + 1)
#cosϕt = cosϕ * cosatnx - sinϕ * sinatnx
sinϕt = sinϕ*cosatnx + cosϕ*sinatnx
σ₀t = sqrt( σ₀^2 + ( ħ*t / (2*m*σ₀) )^2 )
vo*t + sqrt(xo^2 + yo^2) * σ₀t/σ₀ * sinϕt
end
function modelsolver2(Np = 10)
Nt = length(Cronadapt)
xo = [ init() for i = 1:Np ]
#xo = vcat( myrng(a2, a1, Np), myrng(b1, b2, Np) )
xcoord = copy(xo)
ycoord = zeros(Np)
for i in 2:Nt, j in 1:Np
xcoord[j] = rk4(Uₓ, Cronadapt[i], xcoord[j], steps[i] )
end
for (i, x) in enumerate(xo)
y0 = randn()*yh
v0 = 0 #randn()*σv*1e-4
ycoord[i] = yas(Cronadapt[end], x, y0, v0)
end
xcoord, ycoord
end
@time X, Y = modelsolver2(100);
@gp "set title 'Impacts on the screen'" xlab="X, mm" ylab="Y, mm"# "set xrange [-1:1]"
@gp :- 1000X 1000Y "with points notit pt 7 ps 0.5 lc rgb 'black'"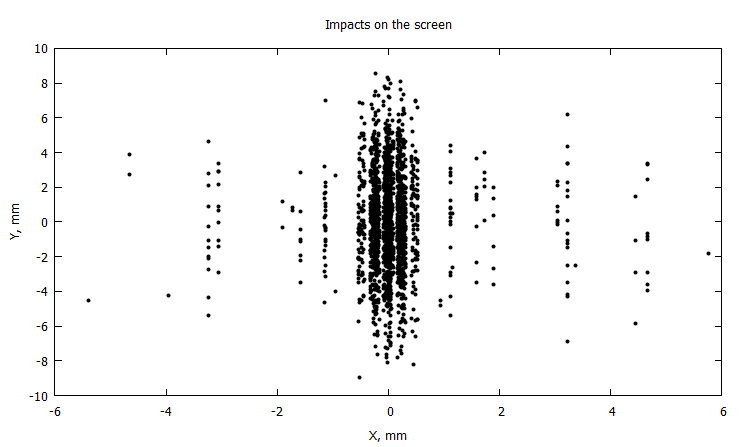
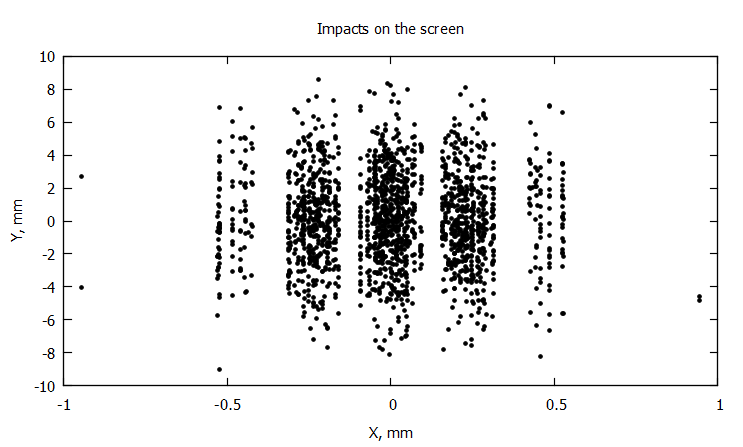
Полосы довольно резкие, без размытия, так как мы нещадно отсеивали горизонтальные составляющие скорости. Если же считать по всем правилам, учитывая разброс начальных положений и скоростей, то картинка очень даже согласуется с реальностью
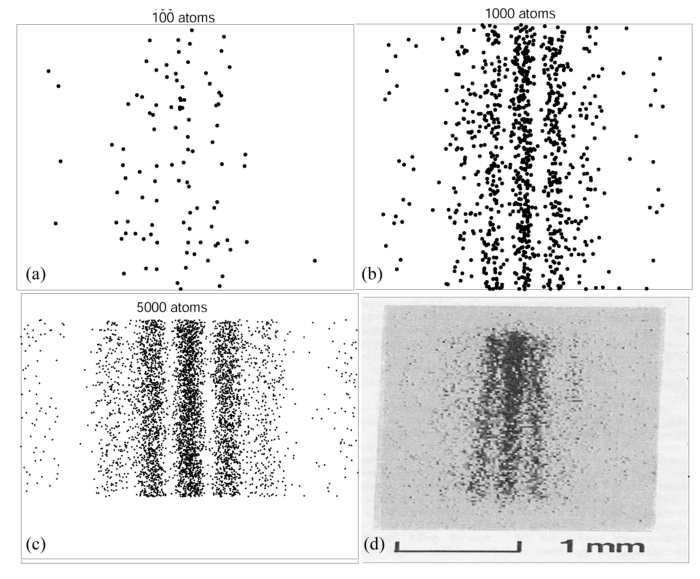
А дальше уже можно собрать эксперимент в одно целое, учесть спины во второй части, добавить эмиссию, добавить возможность удобного изменения размеров щелей, распараллелить, найти эксперименты посвежее — в общем, большой простор для творчества.
- Исходники
- Measurement in the de Broglie-Bohm interpretation: Double-slit, Stern-Gerlach and EPR-B — статья про моделирование типовых квантовых явлений в рамках бомовской механики
- Измерение в интерпретации де Бройля — Бома: опыт с двумя щелями, опыт Штерн-Герлаха и ЭПРБ-эксперимент — Сокращенный перевод М.Х. Шульмана