Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
В данной главе я даю простое и по большей части визуальное объяснение теоремы универсальности. Чтобы следить за материалом этой главы, не обязательно читать предыдущие. Он структурирован в виде самостоятельного эссе. Если у вас есть самое базовое представление о НС, вы должны суметь понять объяснения.
Один из наиболее потрясающих фактов, связанных с нейросетями, заключается в том, что они могут вычислить вообще любую функцию. То есть, допустим, некто даёт вам какую-то сложную и извилистую функцию f(x):

И вне зависимости от этой функции гарантированно существует такая нейросеть, что для любого входа x значение f(x) (или некая близкая к нему аппроксимация) будет являться выходом этой сети, то есть:
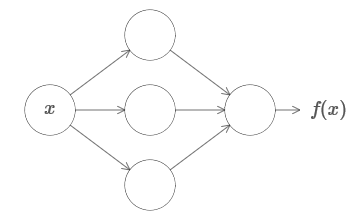
Это работает, даже если это функция многих переменных f=f(x1,…,xm), и со многими значениями. К примеру, вот сеть, вычисляющая функцию с m=3 входами и n=2 выходами:
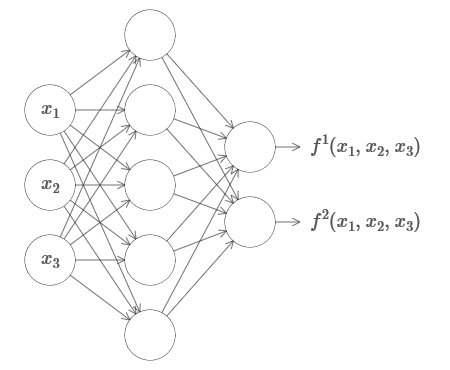
Этот результат говорит о том, что у нейросетей есть определённая универсальность. Неважно, какую функцию мы хотим вычислить, мы знаем, что существует нейросеть, способная сделать это.
Более того, теорема универсальности выполняется, даже если мы ограничим сети единственным слоем между входящими и выходящими нейронами – т.н. одним скрытым слоем. Так что даже сети с очень простой архитектурой могут быть чрезвычайно мощными.
Теорема универсальности хорошо знакома людям, использующим нейросети. Но хотя это так, понимание этого факта не так широко распространено. А большинство объяснений этого слишком технически сложные. К примеру, одна из первых работ, доказывающих этот результат, использовала теорему Хана — Банаха, теорему представлений Риса и немного анализа Фурье. Если вы математик, вам несложно разобраться в этих доказательствах, но большинству людей это не так-то просто. А жаль, поскольку базовые причины универсальности просты и прекрасны.
В данной главе я даю простое и по большей части визуальное объяснение теоремы универсальности. Мы шаг за шагом пройдём по лежащим в её основе идеям. Вы поймёте, почему нейросети действительно могут вычислить любую функцию. Вы поймёте некоторые ограничения этого результата. И поймёте, как результат связан с глубокими НС.
Чтобы следить за материалом этой главы, не обязательно читать предыдущие. Он структурирован в виде самостоятельного эссе. Если у вас есть самое базовое представление о НС, вы должны суметь понять объяснения. Но я буду иногда давать ссылки на предыдущие материалы, чтобы помочь заполнить пробелы в знаниях.
Теоремы универсальности часто встречаются в информатике, так, что иногда мы даже забываем, насколько они потрясающие. Но стоит напоминать себе: возможность вычислить любую произвольную функцию поистине удивительна. Практически любой процесс, который вы можете себе представить, можно свести к вычислению функции. Рассмотрим задачу поиска названия музыкальной композиции на основе краткого отрывка. Это можно считать вычислением функции. Или рассмотрим задачу перевода китайского текста на английский. И это можно считать вычислением функции (на самом деле, многих функций, поскольку существует множество приемлемых вариантов переводов одного текста). Или рассмотрим задачу генерации описания сюжета фильма и качества актёрской игры на основе файла mp4. Это тоже можно рассматривать, как вычисление некоей функции (здесь тоже верна ремарка, сделанная по поводу вариантов перевода текста). Универсальность означает, что в принципе, НС могут выполнять все эти задачи, и множество других.
Конечно, только из того, что мы знаем, что существуют НС, способные, допустим, переводить с китайского на английский, не следует, что у нас есть хорошие техники для создания или даже распознавания такой сети. Это ограничение также применимо к традиционным теоремам универсальности для таких моделей, как Булевы схемы. Но, как мы уже видели в этой книге, у НС есть мощные алгоритмы для выучивания функций. Комбинация алгоритмов обучения и универсальности – смесь привлекательная. Пока что в книге мы концентрировались на обучающих алгоритмах. В данной главе мы сконцентрируемся на универсальности и на том, что она означает.
До того, как объяснить, почему теорема универсальности верна, я хочу упомянуть два подвоха, содержащихся в неформальном заявлении «нейросеть может вычислить любую функцию».
Во-первых, это не значит, что сеть можно использовать для точного подсчёта любой функции. Мы лишь можем получить настолько хорошее приближение, насколько нам нужно. Увеличивая количество скрытых нейронов, мы улучшаем аппроксимацию. К примеру, ранее я иллюстрировал сеть, вычисляющую некую функцию f(x) с использованием трёх скрытых нейронов. Для большинства функций при помощи трёх нейронов можно будет получить только низкокачественное приближение. Увеличив количество скрытых нейронов (допустим, до пяти), мы обычно можем получить улучшенное приближение:
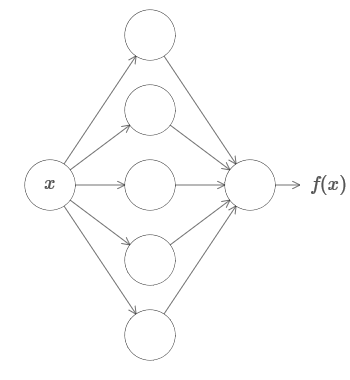
И ещё улучшить ситуацию, увеличивая количество скрытых нейронов и далее.
Чтобы уточнить это утверждение, допустим, нам дали функцию f(x), которую мы хотим вычислить с некоей нужной точностью ε>0. Есть гарантия, что при использовании достаточного количества скрытых нейронов, мы всегда сможем найти НС, выход которой g(x) удовлетворяет уравнению |g(x)−f(x)|<ε для любого x. Иначе говоря, аппроксимация будет достигнута с нужной точностью для любого возможного входного значения.
Второй подвох состоит в том, что функции, которые можно аппроксимировать описанным способом, принадлежат к непрерывному классу. Если функция прерывается, то есть, делает внезапные резкие скачки, то в общем случае её будет невозможно аппроксимировать при помощи НС. И это неудивительно, поскольку наши НС вычисляют непрерывные функции от входных данных. Однако, даже если функция, которую нам очень нужно вычислить, разрывная, часто оказывается достаточно непрерывной аппроксимации. Если это так, то мы можем использовать НС. На практике это ограничение обычно не является важным.
В итоге, боле точным утверждением теоремы универсальности будет то, что НС с одним скрытым слоем можно использовать для аппроксимации любой непрерывной функции с любой желаемой точностью. В данной главе мы докажем чуть менее строгую версию этой теоремы, используя два скрытых слоя вместо одного. В задачах я кратко опишу как это объяснение можно, с небольшими изменениями, адаптировать к доказательству, использующему только один скрытый слой.
Чтобы понять, почему теорема универсальности истинна, начнём с понимания того, как создать НС, аппроксимирующую функцию только с одним входным и одним выходным значением:

Оказывается, что это – суть задачи универсальности. Как только мы поймём этот особый случай, будет довольно легко расширить его на функции со многими входными и выходными значениями.
Чтобы создать понимание того, как сконструировать сеть для подсчёта f, начнём с сети, содержащей едиинственный скрытый слой с двумя скрытыми нейронами, и с выходным слоем, содержащим один выходной нейрон:

Чтобы представить, как работают компоненты сети, сконцентрируемся на верхнем скрытом нейроне. На диаграмме в оригинале статьи можно интерактивно менять вес мышью, кликнув на «w», и сразу же увидеть, как меняется функция, вычисляемая верхним скрытым нейроном:
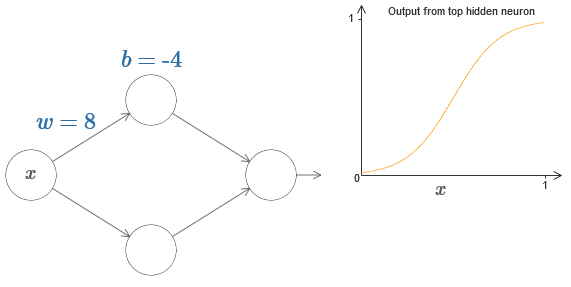
Как мы узнали ранее в книге, скрытый нейрон подсчитывает σ(wx+b), где σ(z) ≡ 1/(1+e−z) – сигмоида. Пока что мы довольно часто использовали эту алгебраическую форму. Однако для доказательства универсальности будет лучше, если мы полностью проигнорируем эту алгебру, и вместо этого будем манипулировать и наблюдать за формой на графике. Это не только поможет лучше почувствовать, что происходит, но и даст нам доказательство универсальности, применимое к другим функциям активации, кроме сигмоиды.
Строго говоря, избранный мною визуальный подход традиционно не считается доказательством. Но я считаю, что визуальный подход даёт больше понимания истинности итогового результата, чем традиционное доказательство. А, конечно, подобное понимание и есть реальная цель доказательства. В предлагаемом мною доказательстве изредка будут попадаться пробелы; я буду давать разумное, но не всегда строгое визуальное доказательство. Если это беспокоит вас, то считайте своей задачей заполнить эти пробелы. Однако не теряйте из виду главной цели: понять, почему теорема универсальности верна.
Чтобы начать с этим доказательством, кликните в оригинальной диаграмме на смещение b и проведите мышью вправо, чтобы увеличить его. Вы увидите, что с увеличением смещения график двигается влево, но не меняет форму.
Затем протяните его влево, чтобы уменьшить смещение. Вы увидите, что график двигается вправо, не меняя форму.
Уменьшите вес до 2-3. Вы увидите, что с уменьшением веса кривая распрямляется. Чтобы кривая не убегала с графика, возможно, придётся подправить смещение.
Наконец, увеличьте вес до значений более 100. Кривая будет становиться всё круче, и в итоге приблизится к ступеньке. Попробуйте подрегулировать смещение так, чтобы её угол находился в районе точки x=0,3. На видео ниже показано, что должно получиться:
Мы можем очень сильно упростить наш анализ, увеличив вес так, чтобы выход реально был хорошей аппроксимацией ступенчатой функции. Ниже я построил выход верхнего скрытого нейрона для веса w=999. Это статичное изображение:
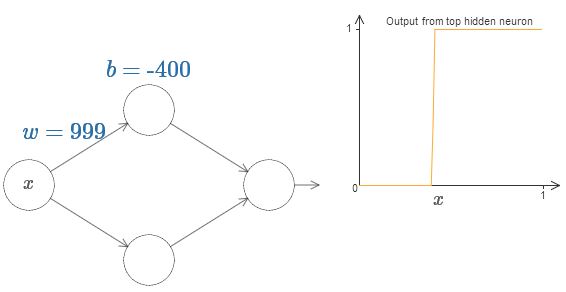
Со ступенчатыми функциями работать немного проще, чем с типичными сигмоидами. Причина в том, что в выходном слое складываются вклады от всех скрытых нейронов. Сумму кучки ступенчатых функций анализировать легко, а вот рассуждать о том, что происходит при сложении кучи кривых в виде сигмоиды – сложнее. Поэтому будет гораздо проще предположить, что наши скрытые нейроны выдаёт ступенчатые функции. Точнее, мы делаем это, фиксируя вес w на некоем очень большом значении, а потом назначая положение ступеньки через смещение. Конечно, работа с выходом, как со ступенчатой функцией – это приближение, но очень хорошее, и пока что мы будем относиться к функции, как к истинно ступенчатой. Позднее я вернусь к обсуждению влияния отклонений от этого приближения.
На каком значении x находится ступенька? Иначе говоря, как положение ступеньки зависит от веса и смещения?
Для ответа на вопрос попытайтесь изменить вес и смещение в интерактивной диаграмме. Можете ли вы понять, как положение ступеньки зависит от w и b? Попрактиковавшись немного, вы сможете убедить себя, что её положение пропорционально b и обратно пропорционально w.
На самом деле, ступенька находится на отметке s=−b/w, как будет видно, если подстроить вес и смещение к следующим значениям:
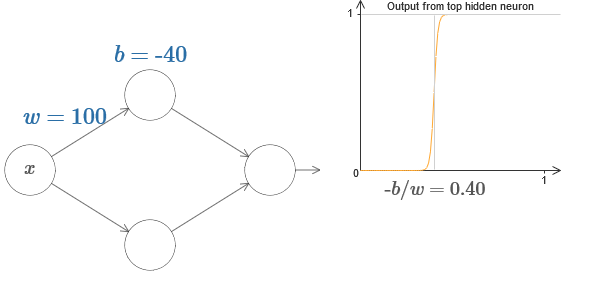
Наши жизни сильно упростятся, если мы будем описывать скрытые нейроны единственным параметром, s, то есть, положением ступеньки, s=−b/w. На следующей интерактивной диаграмме можно менять уже просто s:

Как отмечено выше, мы специально назначили весу w на входе очень большое значение – достаточно большое, чтобы ступенчатая функция стала хорошим приближением. И мы легко можем превратить таким образом параметризованный нейрон обратно к обычной форме, выбрав смещение b=−ws.
Пока что мы концентрировались на выходе только верхнего скрытого нейрона. Давайте посмотрим на поведение всей сети. Предположим, что скрытые нейроны вычисляют ступенчатые функции, заданные параметрами ступенек s1 (верхний нейрон) и s2 (нижний нейрон). Их соответствующими выходными весами будут w1 и w2. Вот наша сеть:
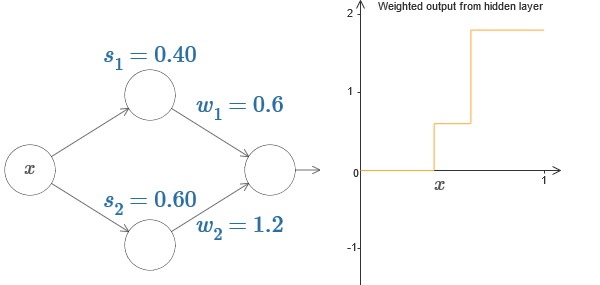
Справа строится график взвешенного выхода w1a1 + w2a2 скрытого слоя. Здесь a1 и a2 — выходы верхнего и нижнего скрытых нейронов, соответственно. Они обозначаются через «a», поскольку их часто называют активациями нейронов.
Кстати, отметим, что выход всей сети равен σ(w1a1 + w2a2 + b), где b – смещение выходного нейрона. Это, очевидно, не то же самое, что взвешенный выход скрытого слоя, график которого мы строим. Но пока мы сконцентрируемся на взвешенном выходе скрытого слоя, и только позднее подумаем, как он связан с выходом всей сети.
Попробуйте на интерактивной диаграмме в оригинале статьи увеличивать и уменьшать ступеньку s1 верхнего скрытого нейрона. Посмотрите, как это меняет взвешенный выход скрытого слоя. Особенно полезно понять, что происходит, когда s1 превышает s2. Вы увидите, что график в этих случаях меняет форму, поскольку мы переходим от ситуации, в которой верхний скрытый нейрон активируется первым, к ситуации, в которой нижний скрытый нейрон активируется первым.
Сходным образом попробуйте манипулировать ступенькой s2 у нижнего скрытого нейрона, и посмотрите, как это меняет общий выход скрытых нейронов.
Попробуйте уменьшать и увеличивать выходные веса. Заметьте, как это масштабирует вклад от соответствующих скрытых нейронов. Что будет, если один из весов сравняется с 0?
Наконец, попробуйте выставить w1 в 0,8, а w2 в -0,8. Получится функция «выступа», с началом в точке s1, концом в точке s2, и высотой 0,8. К примеру, взвешенный выход может выглядеть так:
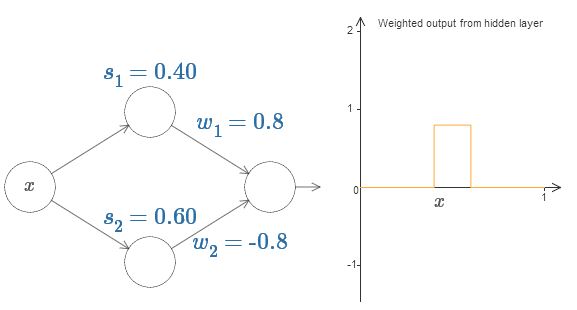
Конечно, выступ можно масштабировать до любой высоты. Давайте использовать один параметр, h, обозначающий высоту. Также для упрощения я избавлюсь от обозначений «s1=…» и «w1=…».
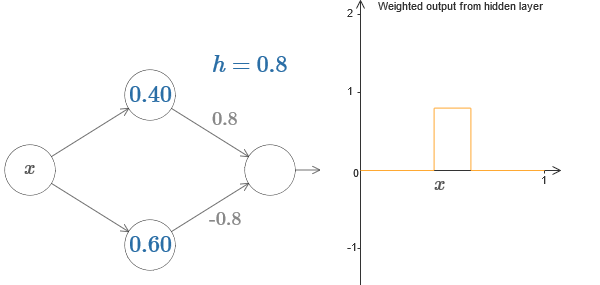
Попробуйте увеличивать и уменьшать значение h, чтобы посмотреть, как меняется высота выступа. Попробуйте сделать h отрицательным. Попробуйте менять точки ступенек, чтобы понаблюдать, как это меняет форму выступа.
Вы увидите, что мы используем наши нейроны не просто, как графические примитивы, но и как более привычные программистам единицы – нечто вроде инструкции if-then-else в программировании:
if вход >= начало ступеньки:
добавить 1 к взвешенному выходу
else:
добавить 0 к взвешенному выходу
По большей части я буду придерживаться графических обозначений. Однако иногда вам будет полезно переключаться на представление if-then-else и размышлять о происходящем в этих терминах.
Мы можем использовать наш трюк с появлением выступа, склеив две части скрытых нейронов вместе в одной сети:
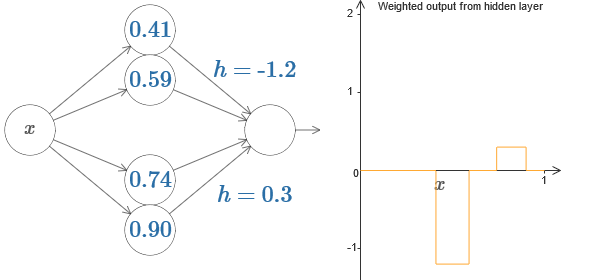
Здесь я опустил веса, просто записав значения h для каждой пары скрытых нейронов. Попробуйте поиграть с обоими значениями h, и понаблюдать, как это меняет график. Подвигайте выступы, меняя точки ступенек.
В более общем случае эту идею можно использовать для получения любого желаемого количества пиков любой высоты. В частности, мы можем разделить интервал [0,1] на большое количество (N) подынтервалов, и использовать N пар скрытых нейронов для получения пиков любой нужной высоты. Посмотрим, как это работает для N=5. Это уже довольно много нейронов, поэтому я немного ужму представления. Извините за сложную диаграмму – я бы мог спрятать сложность за дополнительными абстракциями, но мне кажется, что стоит немного помучаться со сложностью, чтобы лучше почувствовать то, как работают нейросети.
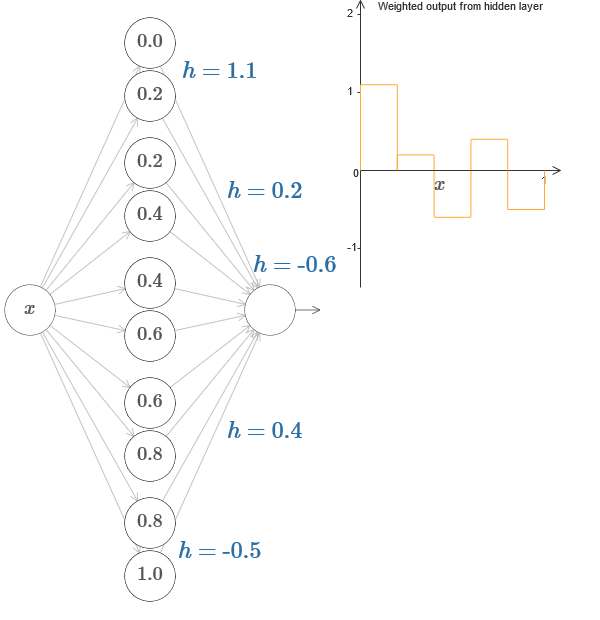
Вы видите, что у нас есть пять пар скрытых нейронов. Точки ступенек соответствующих пар располагаются на значениях 0,1/5, затем 1/5,2/5, и так далее, вплоть до 4/5,5/5. Эти значения фиксированы – мы получаем пять выступов равной ширины на графике.
У каждой пары нейронов есть связанное с нею значение h. Помните, что у выходных связей нейронов есть веса h и –h. В оригинале статьи на диаграмме можно кликнуть на значения h и подвигать их влево-вправо. С изменением высоты меняется и график. Изменяя выходные веса, мы конструируем итоговую функцию!
На диаграмме можно ещё кликнуть по графику, и потаскать высоту ступеньки вверх или вниз. При изменении её высоты вы видите, как изменяется высота соответствующего h. Соответствующим образом меняются выходные веса +h и –h. Иначе говоря, мы напрямую манипулируем функцией, график которой показан справа, и видим эти изменения в значениях h слева. Можно ещё зажать клавишу мыши на одном из выступов, а потом провести мышью влево или вправо, и выступы будут подстраиваться под текущую высоту.
Настало время справиться с задачей.
Вспомним функцию, которую я нарисовал в самом начале главы:

Тогда я не упоминал об этом, но на самом деле она выглядит так:
Она строится для значений x от 0 до 1, а значения по оси y варьируются от 0 до 1.
Очевидно, что эта функция нетривиальная. И вы должны придумать, как подсчитать её с использованием нейросетей.
В наших нейросетях выше мы анализировали взвешенную комбинацию ∑jwjaj выхода скрытых нейронов. Мы знаем, как получить значительный контроль над этой величиной. Но, как я отметил ранее, эта величина не равна выходу сети. Выход сети – это σ(∑jwjaj + b), где b – смещение выходного нейрона. Можем ли мы получить контроль непосредственно над выходом сети?
Решение – разработать такую нейросеть, у которой взвешенный выход скрытого слоя задаётся уравнением σ−1⋅f(x), где σ−1 — обратная функция σ. То есть, мы хотим, чтобы взвешенный выход скрытого слоя был таким:
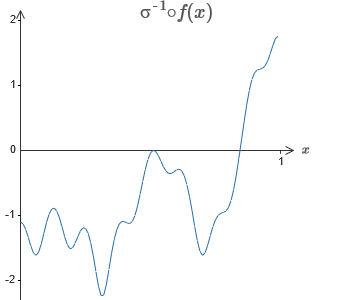
Если это получится, тогда выход всей сети будет хорошей аппроксимацией f(x) (смещение выходного нейрона я установил в 0).
Тогда ваша задача – разработать НС, аппроксимирующую целевую функцию, показанную выше. Чтобы лучше понять происходящее, рекомендую вам решить эту задачу дважды. В первый раз в оригинале статьи кликните на график, и напрямую подстройте высоты разных выступов. Вам довольно легко будет получить хорошее приближение к целевой функции. Степень приближения оценивается средним отклонением, разницей между целевой функцией и той функцией, которую подсчитывает сеть. Ваша задача – привести среднее отклонение к минимальному значению. Задача считается выполненной, когда среднее отклонение не превышает 0,40.
Достигнув успеха, нажмите кнопку Reset, которая случайным образом поменяет выступы. Второй раз не трогайте график, а изменяйте величины h с левой стороны диаграммы, пытаясь привести среднее отклонение к величине 0,40 или менее.
И вот, вы нашли все элементы, необходимые для того, чтобы сеть приблизительно вычисляла функцию f(x)! Аппроксимация получилась грубой, но мы легко можем улучшить результат, просто увеличив количество пар скрытых нейронов, что увеличит количество выступов.
В частности, легко превратить все найденные данные обратно в стандартный вид с параметризацией, используемый для НС. Позвольте быстро напомнить, как это работает.
У первого слоя все веса имеют большое постоянное значение, к примеру, w=1000.
Смещения скрытых нейронов вычисляются через b=−ws. Так что, к примеру, для второго скрытого нейрона s=0,2 превращается в b=−1000×0,2=−200.
Последний слой весов определяется значениями h. Так что, к примеру, значение, выбранное вами для первого h, h= -0,2, означает, что выходные веса двух верхних скрытых нейронов равны -0,2 и 0,2 соответственно. И так далее, для всего слоя выходных весов.
Наконец, смещение выходного нейрона равно 0.
И это всё: у нас получилось полное описание НС, неплохо вычисляющей изначальную целевую функцию. И мы понимаем, как улучшить качество аппроксимации, улучшая количество скрытых нейронов.
Кроме того, в нашей оригинальной целевой функции f(x)=0,2+0,4x2+0,3sin(15x)+0,05cos(50x) нет ничего особенного. Подобную процедуру можно было бы использовать для любой непрерывной функции на отрезках от [0,1] до [0,1]. По сути, мы используем нашу однослойную НС для построения справочной таблицы по функции. И мы можем взять эту идею за основу, чтобы получить обобщённое доказательство универсальности.
Расширим наши результаты на случай множества входящих переменных. Звучит сложно, но все нужные нам идеи можно понять уже для случая всего с двумя входящими переменными. Поэтому рассмотрим случай с двумя входящими переменными.
Начнём с рассмотрения того, что будет, когда у нейрона есть два входа:
У нас есть входы x и y, с соответствующими весами w1 и w2 и смещением b нейрона. Установим вес w2 в 0 и поиграемся с первым, w1, и смещением b, чтобы посмотреть, как они влияют на выход нейрона:
Как видим, при w2=0 вход y не влияет на выход нейрона. Всё происходит так, будто x – единственный вход.
Учитывая это, что, как вы думаете, произойдёт, когда мы увеличим вес w1 до w1=100, а w2 оставим 0? Если это сразу вам непонятно, подумайте немного над этим вопросом. Потом посмотрите следующее видео, где показано, что произойдёт:
Как и ранее, с увеличением входного веса выход приближается к форме ступеньки. Разница в том, что наша ступенчатая функция теперь расположена в трёх измерениях. Как и раньше, мы можем передвигать местоположение ступеньки, изменяя смещение. Угол будет находиться в точке sx≡−b/w1.
Давайте переделаем диаграмму, чтобы параметром было местоположение ступеньки:
Мы предполагаем, что входящий вес у x имеет большое значение – я использовал w1=1000 – и вес w2=0. Число на нейроне – это положение ступеньки, а x над ним напоминает, что мы передвигаем ступеньку по оси x. Естественно, вполне возможно получить ступенчатую функцию по оси y, сделав входящий вес для y большим (допустим, w2=1000), и вес для x равным 0, w1=0:
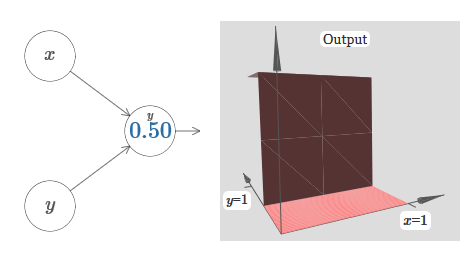
Число на нейроне, опять-таки, обозначает положение ступеньки, а y над ним напоминает, что мы передвигаем ступеньку по оси y. Я бы мог напрямую обозначить веса для x и y, но не стал, поскольку это замусорило бы диаграмму. Но учтите, что маркер y говорит о том, что вес для y большой, а для x равен 0.
Мы можем использовать только что сконструированные нами ступенчатые функции для вычисления функции трёхмерного выступа. Для этого мы возьмём два нейрона, каждый из которых будет вычислять ступенчатую функцию по оси x. Затем мы скомбинируем эти ступенчатые функции с весами h и –h, где h – желаемая высота выступа. Всё это видно на следующей диаграмме:
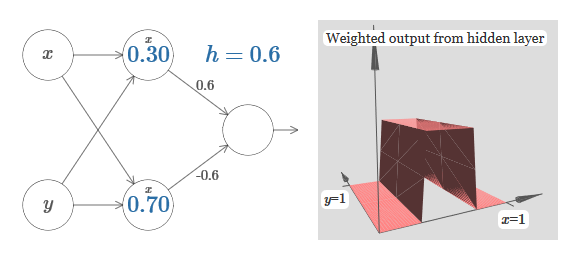
Попробуйте поменять величину h. Посмотрите, как она связана с весами сети. И как она меняет высоту функции выступа справа.
Также попытайтесь изменить точку ступеньки, величина которой установлена в 0,30 в верхнем скрытом нейроне. Посмотрите, как она меняет форму выступа. Что будет, если перенести её за точку 0,70, связанную с нижним скрытым нейроном?
Мы узнали, как построить функцию выступа по оси x. Естественно, мы легко можем сделать функцию выступа и по оси y, используя две ступенчатые функции по оси y. Вспомним, что мы можем сделать это, сделав большие веса на входе y, и установив вес 0 на входе x. И вот, что получится:
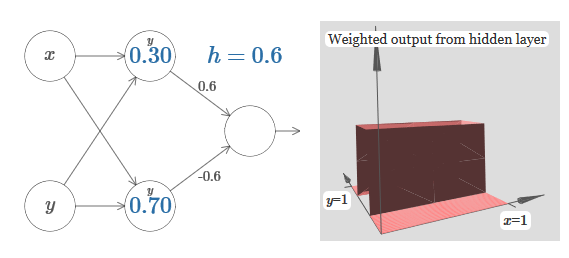
Выглядит почти идентично предыдущей сети! Единственное видимое изменение – маленькие маркеры y на скрытых нейронах. Они напоминают нам о том, что выдают ступенчатые функции для y, а не для x, поэтому на входе y вес очень большой, а на входе x – нулевой, а не наоборот. Как и раньше, я решил не показывать этого непосредственно, чтобы не захламлять рисунок.
Посмотрим, что будет, если мы добавим две функции выступа, одну по оси x, другую по оси y, обе высотой h:

Для упрощения диаграммы связи с нулевым весом я опустил. Пока что я оставил маленькие маркеры x и y на скрытых нейронах, чтобы напомнить, в каких направлениях вычисляются функции выступов. Позже мы и от них откажемся, поскольку они подразумеваются входящей переменной.
Попробуйте менять параметр h. Как видите, из-за этого меняются выходные веса, а также веса обеих функций выступа, x и y.
Созданное нами немного похоже на «функцию башни»:
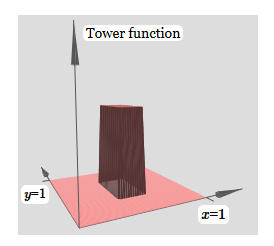
Если мы можем создать такие функции башен, то мы можем использовать их для аппроксимации произвольных функций, просто добавляя башни различных высот в разных местах:
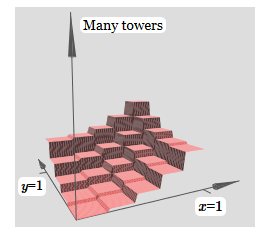
Конечно, мы пока ещё не дошли до создания произвольной функции башни. Мы пока сконструировали что-то вроде центральной башни высоты 2h с окружающим её плато высоты h.
Но мы можем сделать функцию башни. Вспомните, что раньше мы показали, как нейроны можно использовать для реализации инструкции if-then-else:
Это был нейрон с одним входом. А нам нужно применить сходную идею к комбинированному выходу скрытых нейронов:
Если мы правильно выберем порог – к примеру, 3h/2, втиснутый между высотой плато и высотой центральной башни – мы сможем раздавить плато до нуля, и оставить только одну башню.
Представляете, как это сделать? Попробуйте поэкспериментировать со следующей сетью. Теперь мы строим график выхода всей сети, а не просто взвешенный выход скрытого слоя. Это значит, что мы добавляем член смещения к взвешенному выходу от скрытого слоя, и применяем сигмоиду. Сможете ли вы найти значения для h и b, при которых получится башня? Если вы застрянете на этом моменте, вот две подсказки: (1) чтобы выходящий нейрон продемонстрировал правильное поведение в стиле if-then-else, нам нужно, чтобы входящие веса (все h или –h) были крупными; (2) значение b определяет масштаб порога if-then-else.
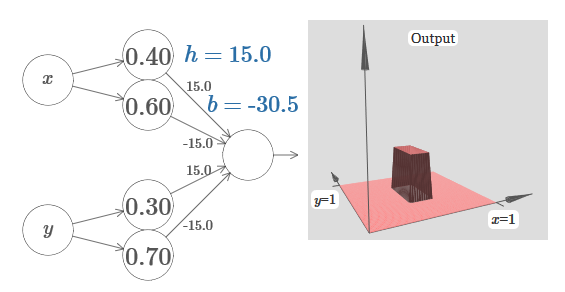
С параметрами по умолчанию выход похож на расплющенную версию предыдущей диаграммы, с башней и плато. Чтобы получить желаемое поведение, нужно увеличить значение h. Это даст нам пороговое поведение if-then-else. Во-вторых, чтобы правильно задать порог, нужно выбрать b ≈ −3h/2.
Вот как это выглядит для h=10:
Даже для относительно скромных величин h мы получаем неплохую функцию башни. И, конечно, мы можем получить сколь угодно красивый результат, увеличивая h и дальше, и удерживая смещение на уровне b=−3h/2.
Давайте попробуем склеить вместе две сети, чтобы подсчитать две разные функции башен. Чтобы соответствующие роли двух подсетей были ясны, я поместил их в отдельные прямоугольники: каждый из них вычисляет функцию башни при помощи описанной выше техники. График справа показывает взвешенный выход второго скрытого слоя, то есть, взвешенную комбинацию функций башен.
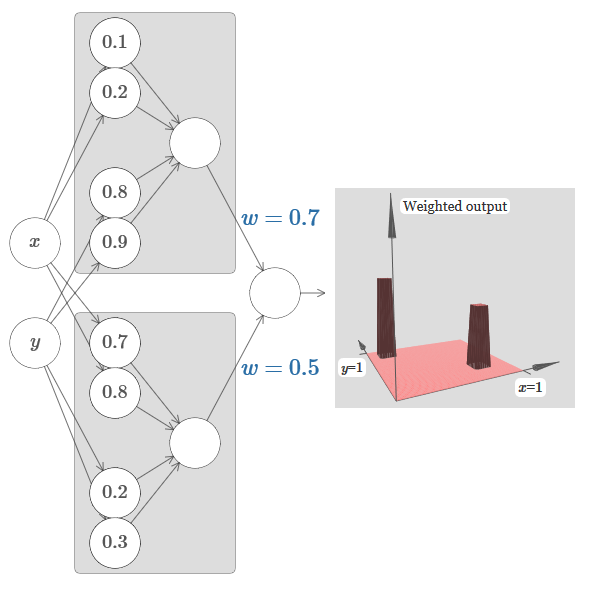
В частности, видно, что изменяя веса в последнем слое, можно менять высоту выходных башен.
Та же идея позволяет вычислять сколько угодно башен. Мы можем сделать их сколь угодно тонкими и высокими. В итоге мы гарантируем, что взвешенный выход второго скрытого слоя аппроксимирует любую нужную функцию двух переменных:
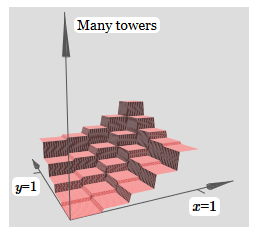
В частности, заставив взвешенный выход второго скрытого слоя хорошо аппроксимировать σ−1⋅f, мы гарантируем, что выход нашей сети будет хорошей аппроксимацией желаемой функции f.
А что же насчёт функций многих переменных?
Попробуем взять три переменных, x1,x2,x3. Следующую сеть можно использовать для подсчёта функции башни в четырёх измерениях?
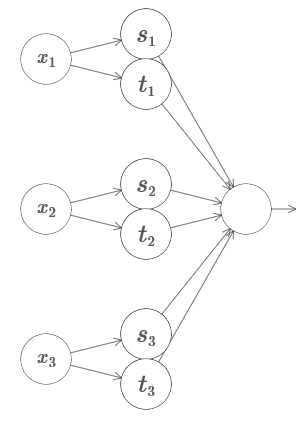
Здесь x1,x2,x3 обозначают вход сети. s1, t1 и так далее – точки ступенек дл нейронов – то есть, все веса в первом слое большие, а смещения назначены так, чтобы точки ступенек равнялись s1, t1, s2,… Веса во втором слое чередуются, +h,−h, где h – некое очень большое число. Выходное смещение равно −5h/2.
Сеть вычисляет функцию, равную 1, при выполнении трёх условий: x1 находится между s1 и t1; x2 находится между s2 и t2; x3 находится между s3 и t3. Сеть равна 0 во всех других местах. Это такая башня, у которой 1 – небольшой участок пространства входа, и 0 – всё остальное.
Склеивая множество таких сетей, мы можем получить сколько угодно башен, и аппроксимировать произвольную функцию трёх переменных. Та же идея работает в m измерений. Меняется только выходное смещение (−m+1/2)h, чтобы правильно втиснуть нужные значения и убрать плато.
Хорошо, теперь мы знаем, как использовать НС для аппроксимации вещественной функции многих переменных. Что насчёт векторных функций f(x1,…,xm) ∈ Rn? Конечно, такую функцию можно рассматривать, просто как n отдельных вещественных функций f1(x1,…,xm), f2(x1,…,xm), и так далее. А потом мы просто склеиваем все сети вместе. Так что с этим легко разобраться.
Мы доказали, что сеть, состоящая из сигмоидных нейронов, может вычислить любую функцию. Вспомним, что в сигмоидном нейроне входы x1,x2,… превращаются на выходе в σ(∑jwjxj + b), где wj — веса, b – смещение, σ — сигмоида.

Что, если мы рассмотрим другой тип нейрона, использующий другую функцию активации, s(z):
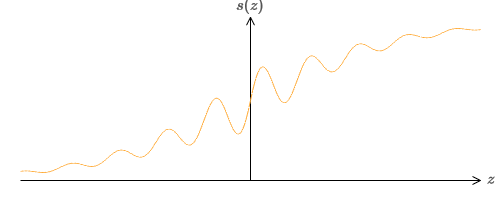
То есть, мы предположим, что если у нейрона на входе будет x1,x2,… веса w1,w2,… и смещение b, то на выходе будет s(∑jwjxj + b).
Мы можем использовать эту функцию активации для получения ступенчатой, точно так же, как в случае с сигмоидой. Попробуйте (в оригинале статьи) на диаграмме задрать вес до, допустим, w=100:
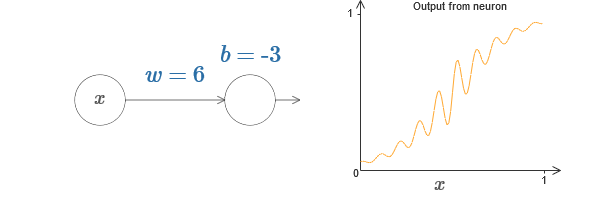

Как и в случае с сигмоидой, из-за этого функция активации сжимается, и в итоге превращается в очень хорошую аппроксимацию ступенчатой функции. Попробуйте поменять смещение, и вы увидите, что мы можем изменить местоположение ступеньки на любое. Поэтому мы можем использовать всё те же трюки, что и ранее, для вычисления любой желаемой функции.
Какие свойства должны быть у s(z), чтобы это сработало? Нам нужно предположить, что s(z) хорошо определена при z→−∞ и z→∞. Эти пределы – это два значения, принимаемых нашей ступенчатой функцией. Нам также нужно предположить, что эти пределы отличаются. Если бы они не отличались, ступеньки бы не получилось, был бы просто плоский график! Но если функция активации s(z) удовлетворяет этим свойствам, основанные на ней нейроны универсально подходят для вычислений.
Покамест мы предполагали, что наши нейроны выдают точные ступенчатые функции. Это неплохое приближение, но лишь приближение. На самом деле существует узкий промежуток отказа, показанный на следующем графике, где функции ведут себя совсем не так, как ступенчатая:
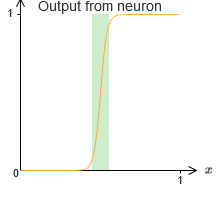
В этом промежутке отказа данное мною объяснение универсальности не работает.
Отказ не такой уж страшный. Задавая достаточно большие входные веса, мы можем делать эти промежутки сколь угодно малыми. Мы можем сделать их гораздо меньшими, чем на графике, невидимыми глазу. Так что, возможно, нам не стоит волноваться из-за этой проблемы.
Тем не менее, хотелось бы иметь некий способ её решения.
Оказывается, её легко решить. Давайте посмотрим на это решение для вычисляющих функции НС со всего одним входом и выходом. Те же идеи сработают и для решения проблемы с большим количеством входов и выходов.
В частности, допустим, мы хотим, чтобы наша сеть вычислила некую функцию f. Как и раньше, мы пытаемся сделать это, проектируя сеть так, чтобы взвешенный выход скрытого слоя нейронов был σ−1⋅f(x):

Если мы будем делать это, используя описанную выше технику, мы заставим скрытые нейроны выдать последовательность функций выступов:
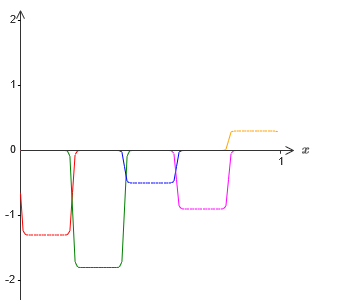
Я, конечно, преувеличил размер промежутков отказа, чтобы их было легче увидеть. Должно быть ясно, что если мы сложим все эти функции выступов, то получим достаточно хорошую аппроксимацию σ−1⋅f(x) везде, кроме промежутков отказа.
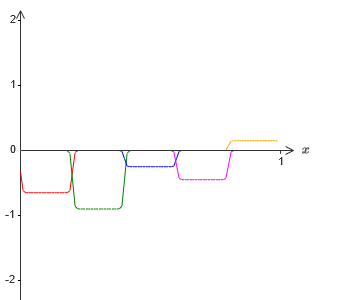
Но, допустим, что вместо использования только что описанной аппроксимации, мы используем набор скрытых нейронов для вычисления аппроксимации половины нашей изначальной целевой функции, то есть, σ−1⋅f(x)/2. Конечно, это будет выглядеть, просто как масштабированная версия последнего графика:
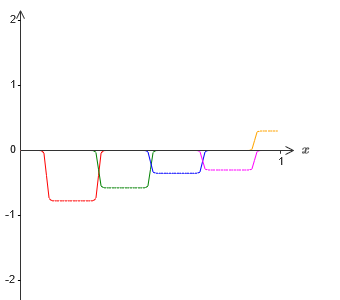
И, допустим, мы заставим ещё один набор скрытых нейронов вычислять приближение к σ−1⋅f(x)/2, однако у него основания выступов будут сдвинуты на половину их ширины:
Теперь у нас есть два разных приближения для σ−1⋅f(x)/2. Если мы сложим две этих аппроксимации, то получим общее приближение к σ−1⋅f(x). У этого общего приближения всё равно будут неточности в небольших промежутках. Но проблема будет меньше, чем раньше – ведь точки, попадающие в промежутки отказа первой аппроксимации, не попадут в промежутки отказа второй аппроксимации. Поэтому аппроксимация в этих промежутках окажется примерно в 2 раза лучше.
Мы можем улучшить ситуацию, добавив большое количество, M, накладывающихся аппроксимаций функции σ−1⋅f(x)/M. Если все промежутки отказа у них будут достаточно узкими, любая тока будет находиться лишь в одном из них. Если использовать достаточно большое количество накладывающихся аппроксимаций M, в итоге получится прекрасное общее приближение.
Рассмотренное здесь объяснение универсальности определённо нельзя назвать практическим описанием того, как подсчитывать функции при помощи нейросетей! В этом смысле оно больше похоже на доказательство универсальности логических вентилей NAND и прочего. Поэтому я в основном пытался сделать так, чтобы эта конструкция была ясной, и ей было просто следовать, не оптимизируя её детали. Однако попытки оптимизировать эту конструкцию могут стать для вас интересным и поучительным упражнением.
Хотя полученный результат нельзя напрямую использовать для создания НС, он важен, поскольку он снимает вопрос вычислимости какой-либо определённой функции при помощи НС. Ответ на такой вопрос всегда будет положительным. Поэтому правильно спрашивать не вычислима ли какая-либо функция, а каков правильный способ её вычисления.
Разработанная нами универсальная конструкция использует всего два скрытых слоя для вычисления произвольной функции. Как мы обсуждали, возможно получить тот же результат при помощи единственного скрытого слоя. Учитывая это, вы можете задуматься, зачем вообще нам нужны глубокие сети, то есть, сети с большим количеством скрытых слоёв. Не можем ли мы просто заменить эти сети на неглубокие, имеющие один скрытый слой?
Хотя, в принципе, это возможно, существуют хорошие практические причины для использования глубоких нейросетей. Как описано в главе 1, у глубоких НС есть иерархическая структура, позволяющая им хорошо адаптироваться для изучения иерархических знаний, которые оказываются полезными для решения реальных проблем. Более конкретно, при решении таких задач, как распознавание образов, полезно бывает использовать систему, понимающую не только отдельные пиксели, но и всё более сложные концепции: от границ до простых геометрических фигур, и далее, вплоть до сложных сцен с участием нескольких объектов. В более поздних главах мы увидим свидетельства, говорящие в пользу того, что глубокие НС смогут лучше неглубоких справиться с изучением подобных иерархий знания. Подытоживая: универсальность говорит нам, что НС могут подсчитать любую функцию; эмпирические свидетельства говорят о том, что глубокие НС лучше адаптированы к изучениям функций, полезных для решения многих задач реального мира.
Содержание
- Глава 1: использование нейросетей для распознавания рукописных цифр
- Глава 2: как работает алгоритм обратного распространения
- Глава 3:
- ч.1: улучшение способа обучения нейросетей
- ч.2: почему регуляризация помогает уменьшать переобучение?
- ч.3: как выбрать гиперпараметры нейросети?
- ч.1: улучшение способа обучения нейросетей
Один из наиболее потрясающих фактов, связанных с нейросетями, заключается в том, что они могут вычислить вообще любую функцию. То есть, допустим, некто даёт вам какую-то сложную и извилистую функцию f(x):

И вне зависимости от этой функции гарантированно существует такая нейросеть, что для любого входа x значение f(x) (или некая близкая к нему аппроксимация) будет являться выходом этой сети, то есть:

Это работает, даже если это функция многих переменных f=f(x1,…,xm), и со многими значениями. К примеру, вот сеть, вычисляющая функцию с m=3 входами и n=2 выходами:

Этот результат говорит о том, что у нейросетей есть определённая универсальность. Неважно, какую функцию мы хотим вычислить, мы знаем, что существует нейросеть, способная сделать это.
Более того, теорема универсальности выполняется, даже если мы ограничим сети единственным слоем между входящими и выходящими нейронами – т.н. одним скрытым слоем. Так что даже сети с очень простой архитектурой могут быть чрезвычайно мощными.
Теорема универсальности хорошо знакома людям, использующим нейросети. Но хотя это так, понимание этого факта не так широко распространено. А большинство объяснений этого слишком технически сложные. К примеру, одна из первых работ, доказывающих этот результат, использовала теорему Хана — Банаха, теорему представлений Риса и немного анализа Фурье. Если вы математик, вам несложно разобраться в этих доказательствах, но большинству людей это не так-то просто. А жаль, поскольку базовые причины универсальности просты и прекрасны.
В данной главе я даю простое и по большей части визуальное объяснение теоремы универсальности. Мы шаг за шагом пройдём по лежащим в её основе идеям. Вы поймёте, почему нейросети действительно могут вычислить любую функцию. Вы поймёте некоторые ограничения этого результата. И поймёте, как результат связан с глубокими НС.
Чтобы следить за материалом этой главы, не обязательно читать предыдущие. Он структурирован в виде самостоятельного эссе. Если у вас есть самое базовое представление о НС, вы должны суметь понять объяснения. Но я буду иногда давать ссылки на предыдущие материалы, чтобы помочь заполнить пробелы в знаниях.
Теоремы универсальности часто встречаются в информатике, так, что иногда мы даже забываем, насколько они потрясающие. Но стоит напоминать себе: возможность вычислить любую произвольную функцию поистине удивительна. Практически любой процесс, который вы можете себе представить, можно свести к вычислению функции. Рассмотрим задачу поиска названия музыкальной композиции на основе краткого отрывка. Это можно считать вычислением функции. Или рассмотрим задачу перевода китайского текста на английский. И это можно считать вычислением функции (на самом деле, многих функций, поскольку существует множество приемлемых вариантов переводов одного текста). Или рассмотрим задачу генерации описания сюжета фильма и качества актёрской игры на основе файла mp4. Это тоже можно рассматривать, как вычисление некоей функции (здесь тоже верна ремарка, сделанная по поводу вариантов перевода текста). Универсальность означает, что в принципе, НС могут выполнять все эти задачи, и множество других.
Конечно, только из того, что мы знаем, что существуют НС, способные, допустим, переводить с китайского на английский, не следует, что у нас есть хорошие техники для создания или даже распознавания такой сети. Это ограничение также применимо к традиционным теоремам универсальности для таких моделей, как Булевы схемы. Но, как мы уже видели в этой книге, у НС есть мощные алгоритмы для выучивания функций. Комбинация алгоритмов обучения и универсальности – смесь привлекательная. Пока что в книге мы концентрировались на обучающих алгоритмах. В данной главе мы сконцентрируемся на универсальности и на том, что она означает.
Два подвоха
До того, как объяснить, почему теорема универсальности верна, я хочу упомянуть два подвоха, содержащихся в неформальном заявлении «нейросеть может вычислить любую функцию».
Во-первых, это не значит, что сеть можно использовать для точного подсчёта любой функции. Мы лишь можем получить настолько хорошее приближение, насколько нам нужно. Увеличивая количество скрытых нейронов, мы улучшаем аппроксимацию. К примеру, ранее я иллюстрировал сеть, вычисляющую некую функцию f(x) с использованием трёх скрытых нейронов. Для большинства функций при помощи трёх нейронов можно будет получить только низкокачественное приближение. Увеличив количество скрытых нейронов (допустим, до пяти), мы обычно можем получить улучшенное приближение:

И ещё улучшить ситуацию, увеличивая количество скрытых нейронов и далее.
Чтобы уточнить это утверждение, допустим, нам дали функцию f(x), которую мы хотим вычислить с некоей нужной точностью ε>0. Есть гарантия, что при использовании достаточного количества скрытых нейронов, мы всегда сможем найти НС, выход которой g(x) удовлетворяет уравнению |g(x)−f(x)|<ε для любого x. Иначе говоря, аппроксимация будет достигнута с нужной точностью для любого возможного входного значения.
Второй подвох состоит в том, что функции, которые можно аппроксимировать описанным способом, принадлежат к непрерывному классу. Если функция прерывается, то есть, делает внезапные резкие скачки, то в общем случае её будет невозможно аппроксимировать при помощи НС. И это неудивительно, поскольку наши НС вычисляют непрерывные функции от входных данных. Однако, даже если функция, которую нам очень нужно вычислить, разрывная, часто оказывается достаточно непрерывной аппроксимации. Если это так, то мы можем использовать НС. На практике это ограничение обычно не является важным.
В итоге, боле точным утверждением теоремы универсальности будет то, что НС с одним скрытым слоем можно использовать для аппроксимации любой непрерывной функции с любой желаемой точностью. В данной главе мы докажем чуть менее строгую версию этой теоремы, используя два скрытых слоя вместо одного. В задачах я кратко опишу как это объяснение можно, с небольшими изменениями, адаптировать к доказательству, использующему только один скрытый слой.
Универсальность с одним входным и одним выходным значением
Чтобы понять, почему теорема универсальности истинна, начнём с понимания того, как создать НС, аппроксимирующую функцию только с одним входным и одним выходным значением:

Оказывается, что это – суть задачи универсальности. Как только мы поймём этот особый случай, будет довольно легко расширить его на функции со многими входными и выходными значениями.
Чтобы создать понимание того, как сконструировать сеть для подсчёта f, начнём с сети, содержащей едиинственный скрытый слой с двумя скрытыми нейронами, и с выходным слоем, содержащим один выходной нейрон:

Чтобы представить, как работают компоненты сети, сконцентрируемся на верхнем скрытом нейроне. На диаграмме в оригинале статьи можно интерактивно менять вес мышью, кликнув на «w», и сразу же увидеть, как меняется функция, вычисляемая верхним скрытым нейроном:

Как мы узнали ранее в книге, скрытый нейрон подсчитывает σ(wx+b), где σ(z) ≡ 1/(1+e−z) – сигмоида. Пока что мы довольно часто использовали эту алгебраическую форму. Однако для доказательства универсальности будет лучше, если мы полностью проигнорируем эту алгебру, и вместо этого будем манипулировать и наблюдать за формой на графике. Это не только поможет лучше почувствовать, что происходит, но и даст нам доказательство универсальности, применимое к другим функциям активации, кроме сигмоиды.
Строго говоря, избранный мною визуальный подход традиционно не считается доказательством. Но я считаю, что визуальный подход даёт больше понимания истинности итогового результата, чем традиционное доказательство. А, конечно, подобное понимание и есть реальная цель доказательства. В предлагаемом мною доказательстве изредка будут попадаться пробелы; я буду давать разумное, но не всегда строгое визуальное доказательство. Если это беспокоит вас, то считайте своей задачей заполнить эти пробелы. Однако не теряйте из виду главной цели: понять, почему теорема универсальности верна.
Чтобы начать с этим доказательством, кликните в оригинальной диаграмме на смещение b и проведите мышью вправо, чтобы увеличить его. Вы увидите, что с увеличением смещения график двигается влево, но не меняет форму.
Затем протяните его влево, чтобы уменьшить смещение. Вы увидите, что график двигается вправо, не меняя форму.
Уменьшите вес до 2-3. Вы увидите, что с уменьшением веса кривая распрямляется. Чтобы кривая не убегала с графика, возможно, придётся подправить смещение.
Наконец, увеличьте вес до значений более 100. Кривая будет становиться всё круче, и в итоге приблизится к ступеньке. Попробуйте подрегулировать смещение так, чтобы её угол находился в районе точки x=0,3. На видео ниже показано, что должно получиться:
Мы можем очень сильно упростить наш анализ, увеличив вес так, чтобы выход реально был хорошей аппроксимацией ступенчатой функции. Ниже я построил выход верхнего скрытого нейрона для веса w=999. Это статичное изображение:

Со ступенчатыми функциями работать немного проще, чем с типичными сигмоидами. Причина в том, что в выходном слое складываются вклады от всех скрытых нейронов. Сумму кучки ступенчатых функций анализировать легко, а вот рассуждать о том, что происходит при сложении кучи кривых в виде сигмоиды – сложнее. Поэтому будет гораздо проще предположить, что наши скрытые нейроны выдаёт ступенчатые функции. Точнее, мы делаем это, фиксируя вес w на некоем очень большом значении, а потом назначая положение ступеньки через смещение. Конечно, работа с выходом, как со ступенчатой функцией – это приближение, но очень хорошее, и пока что мы будем относиться к функции, как к истинно ступенчатой. Позднее я вернусь к обсуждению влияния отклонений от этого приближения.
На каком значении x находится ступенька? Иначе говоря, как положение ступеньки зависит от веса и смещения?
Для ответа на вопрос попытайтесь изменить вес и смещение в интерактивной диаграмме. Можете ли вы понять, как положение ступеньки зависит от w и b? Попрактиковавшись немного, вы сможете убедить себя, что её положение пропорционально b и обратно пропорционально w.
На самом деле, ступенька находится на отметке s=−b/w, как будет видно, если подстроить вес и смещение к следующим значениям:

Наши жизни сильно упростятся, если мы будем описывать скрытые нейроны единственным параметром, s, то есть, положением ступеньки, s=−b/w. На следующей интерактивной диаграмме можно менять уже просто s:

Как отмечено выше, мы специально назначили весу w на входе очень большое значение – достаточно большое, чтобы ступенчатая функция стала хорошим приближением. И мы легко можем превратить таким образом параметризованный нейрон обратно к обычной форме, выбрав смещение b=−ws.
Пока что мы концентрировались на выходе только верхнего скрытого нейрона. Давайте посмотрим на поведение всей сети. Предположим, что скрытые нейроны вычисляют ступенчатые функции, заданные параметрами ступенек s1 (верхний нейрон) и s2 (нижний нейрон). Их соответствующими выходными весами будут w1 и w2. Вот наша сеть:

Справа строится график взвешенного выхода w1a1 + w2a2 скрытого слоя. Здесь a1 и a2 — выходы верхнего и нижнего скрытых нейронов, соответственно. Они обозначаются через «a», поскольку их часто называют активациями нейронов.
Кстати, отметим, что выход всей сети равен σ(w1a1 + w2a2 + b), где b – смещение выходного нейрона. Это, очевидно, не то же самое, что взвешенный выход скрытого слоя, график которого мы строим. Но пока мы сконцентрируемся на взвешенном выходе скрытого слоя, и только позднее подумаем, как он связан с выходом всей сети.
Попробуйте на интерактивной диаграмме в оригинале статьи увеличивать и уменьшать ступеньку s1 верхнего скрытого нейрона. Посмотрите, как это меняет взвешенный выход скрытого слоя. Особенно полезно понять, что происходит, когда s1 превышает s2. Вы увидите, что график в этих случаях меняет форму, поскольку мы переходим от ситуации, в которой верхний скрытый нейрон активируется первым, к ситуации, в которой нижний скрытый нейрон активируется первым.
Сходным образом попробуйте манипулировать ступенькой s2 у нижнего скрытого нейрона, и посмотрите, как это меняет общий выход скрытых нейронов.
Попробуйте уменьшать и увеличивать выходные веса. Заметьте, как это масштабирует вклад от соответствующих скрытых нейронов. Что будет, если один из весов сравняется с 0?
Наконец, попробуйте выставить w1 в 0,8, а w2 в -0,8. Получится функция «выступа», с началом в точке s1, концом в точке s2, и высотой 0,8. К примеру, взвешенный выход может выглядеть так:

Конечно, выступ можно масштабировать до любой высоты. Давайте использовать один параметр, h, обозначающий высоту. Также для упрощения я избавлюсь от обозначений «s1=…» и «w1=…».

Попробуйте увеличивать и уменьшать значение h, чтобы посмотреть, как меняется высота выступа. Попробуйте сделать h отрицательным. Попробуйте менять точки ступенек, чтобы понаблюдать, как это меняет форму выступа.
Вы увидите, что мы используем наши нейроны не просто, как графические примитивы, но и как более привычные программистам единицы – нечто вроде инструкции if-then-else в программировании:
if вход >= начало ступеньки:
добавить 1 к взвешенному выходу
else:
добавить 0 к взвешенному выходу
По большей части я буду придерживаться графических обозначений. Однако иногда вам будет полезно переключаться на представление if-then-else и размышлять о происходящем в этих терминах.
Мы можем использовать наш трюк с появлением выступа, склеив две части скрытых нейронов вместе в одной сети:

Здесь я опустил веса, просто записав значения h для каждой пары скрытых нейронов. Попробуйте поиграть с обоими значениями h, и понаблюдать, как это меняет график. Подвигайте выступы, меняя точки ступенек.
В более общем случае эту идею можно использовать для получения любого желаемого количества пиков любой высоты. В частности, мы можем разделить интервал [0,1] на большое количество (N) подынтервалов, и использовать N пар скрытых нейронов для получения пиков любой нужной высоты. Посмотрим, как это работает для N=5. Это уже довольно много нейронов, поэтому я немного ужму представления. Извините за сложную диаграмму – я бы мог спрятать сложность за дополнительными абстракциями, но мне кажется, что стоит немного помучаться со сложностью, чтобы лучше почувствовать то, как работают нейросети.

Вы видите, что у нас есть пять пар скрытых нейронов. Точки ступенек соответствующих пар располагаются на значениях 0,1/5, затем 1/5,2/5, и так далее, вплоть до 4/5,5/5. Эти значения фиксированы – мы получаем пять выступов равной ширины на графике.
У каждой пары нейронов есть связанное с нею значение h. Помните, что у выходных связей нейронов есть веса h и –h. В оригинале статьи на диаграмме можно кликнуть на значения h и подвигать их влево-вправо. С изменением высоты меняется и график. Изменяя выходные веса, мы конструируем итоговую функцию!
На диаграмме можно ещё кликнуть по графику, и потаскать высоту ступеньки вверх или вниз. При изменении её высоты вы видите, как изменяется высота соответствующего h. Соответствующим образом меняются выходные веса +h и –h. Иначе говоря, мы напрямую манипулируем функцией, график которой показан справа, и видим эти изменения в значениях h слева. Можно ещё зажать клавишу мыши на одном из выступов, а потом провести мышью влево или вправо, и выступы будут подстраиваться под текущую высоту.
Настало время справиться с задачей.
Вспомним функцию, которую я нарисовал в самом начале главы:

Тогда я не упоминал об этом, но на самом деле она выглядит так:
Она строится для значений x от 0 до 1, а значения по оси y варьируются от 0 до 1.
Очевидно, что эта функция нетривиальная. И вы должны придумать, как подсчитать её с использованием нейросетей.
В наших нейросетях выше мы анализировали взвешенную комбинацию ∑jwjaj выхода скрытых нейронов. Мы знаем, как получить значительный контроль над этой величиной. Но, как я отметил ранее, эта величина не равна выходу сети. Выход сети – это σ(∑jwjaj + b), где b – смещение выходного нейрона. Можем ли мы получить контроль непосредственно над выходом сети?
Решение – разработать такую нейросеть, у которой взвешенный выход скрытого слоя задаётся уравнением σ−1⋅f(x), где σ−1 — обратная функция σ. То есть, мы хотим, чтобы взвешенный выход скрытого слоя был таким:

Если это получится, тогда выход всей сети будет хорошей аппроксимацией f(x) (смещение выходного нейрона я установил в 0).
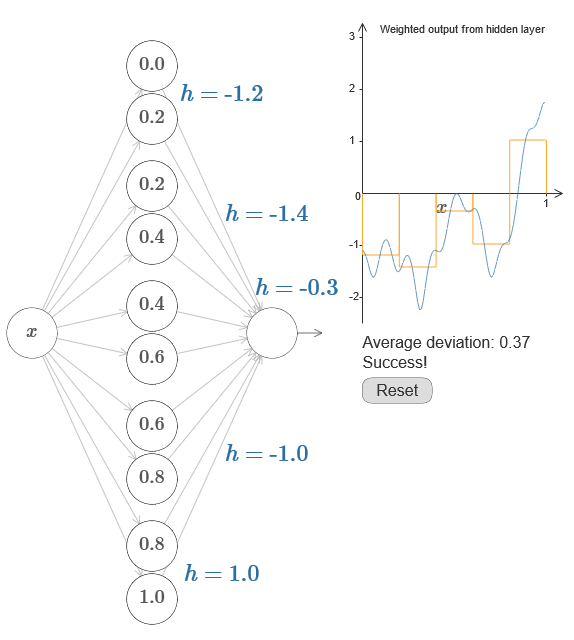
Тогда ваша задача – разработать НС, аппроксимирующую целевую функцию, показанную выше. Чтобы лучше понять происходящее, рекомендую вам решить эту задачу дважды. В первый раз в оригинале статьи кликните на график, и напрямую подстройте высоты разных выступов. Вам довольно легко будет получить хорошее приближение к целевой функции. Степень приближения оценивается средним отклонением, разницей между целевой функцией и той функцией, которую подсчитывает сеть. Ваша задача – привести среднее отклонение к минимальному значению. Задача считается выполненной, когда среднее отклонение не превышает 0,40.

Достигнув успеха, нажмите кнопку Reset, которая случайным образом поменяет выступы. Второй раз не трогайте график, а изменяйте величины h с левой стороны диаграммы, пытаясь привести среднее отклонение к величине 0,40 или менее.
И вот, вы нашли все элементы, необходимые для того, чтобы сеть приблизительно вычисляла функцию f(x)! Аппроксимация получилась грубой, но мы легко можем улучшить результат, просто увеличив количество пар скрытых нейронов, что увеличит количество выступов.
В частности, легко превратить все найденные данные обратно в стандартный вид с параметризацией, используемый для НС. Позвольте быстро напомнить, как это работает.
У первого слоя все веса имеют большое постоянное значение, к примеру, w=1000.
Смещения скрытых нейронов вычисляются через b=−ws. Так что, к примеру, для второго скрытого нейрона s=0,2 превращается в b=−1000×0,2=−200.
Последний слой весов определяется значениями h. Так что, к примеру, значение, выбранное вами для первого h, h= -0,2, означает, что выходные веса двух верхних скрытых нейронов равны -0,2 и 0,2 соответственно. И так далее, для всего слоя выходных весов.
Наконец, смещение выходного нейрона равно 0.
И это всё: у нас получилось полное описание НС, неплохо вычисляющей изначальную целевую функцию. И мы понимаем, как улучшить качество аппроксимации, улучшая количество скрытых нейронов.
Кроме того, в нашей оригинальной целевой функции f(x)=0,2+0,4x2+0,3sin(15x)+0,05cos(50x) нет ничего особенного. Подобную процедуру можно было бы использовать для любой непрерывной функции на отрезках от [0,1] до [0,1]. По сути, мы используем нашу однослойную НС для построения справочной таблицы по функции. И мы можем взять эту идею за основу, чтобы получить обобщённое доказательство универсальности.
Функция от многих параметров
Расширим наши результаты на случай множества входящих переменных. Звучит сложно, но все нужные нам идеи можно понять уже для случая всего с двумя входящими переменными. Поэтому рассмотрим случай с двумя входящими переменными.
Начнём с рассмотрения того, что будет, когда у нейрона есть два входа:

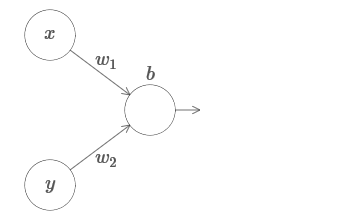
У нас есть входы x и y, с соответствующими весами w1 и w2 и смещением b нейрона. Установим вес w2 в 0 и поиграемся с первым, w1, и смещением b, чтобы посмотреть, как они влияют на выход нейрона:

Как видим, при w2=0 вход y не влияет на выход нейрона. Всё происходит так, будто x – единственный вход.
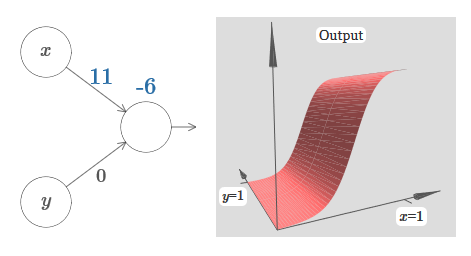
Учитывая это, что, как вы думаете, произойдёт, когда мы увеличим вес w1 до w1=100, а w2 оставим 0? Если это сразу вам непонятно, подумайте немного над этим вопросом. Потом посмотрите следующее видео, где показано, что произойдёт:
Как и ранее, с увеличением входного веса выход приближается к форме ступеньки. Разница в том, что наша ступенчатая функция теперь расположена в трёх измерениях. Как и раньше, мы можем передвигать местоположение ступеньки, изменяя смещение. Угол будет находиться в точке sx≡−b/w1.
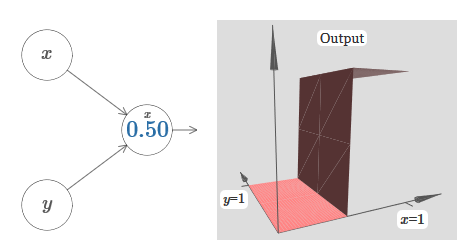
Давайте переделаем диаграмму, чтобы параметром было местоположение ступеньки:

Мы предполагаем, что входящий вес у x имеет большое значение – я использовал w1=1000 – и вес w2=0. Число на нейроне – это положение ступеньки, а x над ним напоминает, что мы передвигаем ступеньку по оси x. Естественно, вполне возможно получить ступенчатую функцию по оси y, сделав входящий вес для y большим (допустим, w2=1000), и вес для x равным 0, w1=0:

Число на нейроне, опять-таки, обозначает положение ступеньки, а y над ним напоминает, что мы передвигаем ступеньку по оси y. Я бы мог напрямую обозначить веса для x и y, но не стал, поскольку это замусорило бы диаграмму. Но учтите, что маркер y говорит о том, что вес для y большой, а для x равен 0.
Мы можем использовать только что сконструированные нами ступенчатые функции для вычисления функции трёхмерного выступа. Для этого мы возьмём два нейрона, каждый из которых будет вычислять ступенчатую функцию по оси x. Затем мы скомбинируем эти ступенчатые функции с весами h и –h, где h – желаемая высота выступа. Всё это видно на следующей диаграмме:

Попробуйте поменять величину h. Посмотрите, как она связана с весами сети. И как она меняет высоту функции выступа справа.
Также попытайтесь изменить точку ступеньки, величина которой установлена в 0,30 в верхнем скрытом нейроне. Посмотрите, как она меняет форму выступа. Что будет, если перенести её за точку 0,70, связанную с нижним скрытым нейроном?
Мы узнали, как построить функцию выступа по оси x. Естественно, мы легко можем сделать функцию выступа и по оси y, используя две ступенчатые функции по оси y. Вспомним, что мы можем сделать это, сделав большие веса на входе y, и установив вес 0 на входе x. И вот, что получится:

Выглядит почти идентично предыдущей сети! Единственное видимое изменение – маленькие маркеры y на скрытых нейронах. Они напоминают нам о том, что выдают ступенчатые функции для y, а не для x, поэтому на входе y вес очень большой, а на входе x – нулевой, а не наоборот. Как и раньше, я решил не показывать этого непосредственно, чтобы не захламлять рисунок.
Посмотрим, что будет, если мы добавим две функции выступа, одну по оси x, другую по оси y, обе высотой h:

Для упрощения диаграммы связи с нулевым весом я опустил. Пока что я оставил маленькие маркеры x и y на скрытых нейронах, чтобы напомнить, в каких направлениях вычисляются функции выступов. Позже мы и от них откажемся, поскольку они подразумеваются входящей переменной.
Попробуйте менять параметр h. Как видите, из-за этого меняются выходные веса, а также веса обеих функций выступа, x и y.
Созданное нами немного похоже на «функцию башни»:

Если мы можем создать такие функции башен, то мы можем использовать их для аппроксимации произвольных функций, просто добавляя башни различных высот в разных местах:

Конечно, мы пока ещё не дошли до создания произвольной функции башни. Мы пока сконструировали что-то вроде центральной башни высоты 2h с окружающим её плато высоты h.
Но мы можем сделать функцию башни. Вспомните, что раньше мы показали, как нейроны можно использовать для реализации инструкции if-then-else:
if вход >= порог:
выход 1
else:
выход 0Это был нейрон с одним входом. А нам нужно применить сходную идею к комбинированному выходу скрытых нейронов:
if скомбинированный выход скрытых нейронов >= порог:
выход 1
else:
выход 0Если мы правильно выберем порог – к примеру, 3h/2, втиснутый между высотой плато и высотой центральной башни – мы сможем раздавить плато до нуля, и оставить только одну башню.
Представляете, как это сделать? Попробуйте поэкспериментировать со следующей сетью. Теперь мы строим график выхода всей сети, а не просто взвешенный выход скрытого слоя. Это значит, что мы добавляем член смещения к взвешенному выходу от скрытого слоя, и применяем сигмоиду. Сможете ли вы найти значения для h и b, при которых получится башня? Если вы застрянете на этом моменте, вот две подсказки: (1) чтобы выходящий нейрон продемонстрировал правильное поведение в стиле if-then-else, нам нужно, чтобы входящие веса (все h или –h) были крупными; (2) значение b определяет масштаб порога if-then-else.

С параметрами по умолчанию выход похож на расплющенную версию предыдущей диаграммы, с башней и плато. Чтобы получить желаемое поведение, нужно увеличить значение h. Это даст нам пороговое поведение if-then-else. Во-вторых, чтобы правильно задать порог, нужно выбрать b ≈ −3h/2.
Вот как это выглядит для h=10:
Даже для относительно скромных величин h мы получаем неплохую функцию башни. И, конечно, мы можем получить сколь угодно красивый результат, увеличивая h и дальше, и удерживая смещение на уровне b=−3h/2.
Давайте попробуем склеить вместе две сети, чтобы подсчитать две разные функции башен. Чтобы соответствующие роли двух подсетей были ясны, я поместил их в отдельные прямоугольники: каждый из них вычисляет функцию башни при помощи описанной выше техники. График справа показывает взвешенный выход второго скрытого слоя, то есть, взвешенную комбинацию функций башен.

В частности, видно, что изменяя веса в последнем слое, можно менять высоту выходных башен.
Та же идея позволяет вычислять сколько угодно башен. Мы можем сделать их сколь угодно тонкими и высокими. В итоге мы гарантируем, что взвешенный выход второго скрытого слоя аппроксимирует любую нужную функцию двух переменных:

В частности, заставив взвешенный выход второго скрытого слоя хорошо аппроксимировать σ−1⋅f, мы гарантируем, что выход нашей сети будет хорошей аппроксимацией желаемой функции f.
А что же насчёт функций многих переменных?
Попробуем взять три переменных, x1,x2,x3. Следующую сеть можно использовать для подсчёта функции башни в четырёх измерениях?

Здесь x1,x2,x3 обозначают вход сети. s1, t1 и так далее – точки ступенек дл нейронов – то есть, все веса в первом слое большие, а смещения назначены так, чтобы точки ступенек равнялись s1, t1, s2,… Веса во втором слое чередуются, +h,−h, где h – некое очень большое число. Выходное смещение равно −5h/2.
Сеть вычисляет функцию, равную 1, при выполнении трёх условий: x1 находится между s1 и t1; x2 находится между s2 и t2; x3 находится между s3 и t3. Сеть равна 0 во всех других местах. Это такая башня, у которой 1 – небольшой участок пространства входа, и 0 – всё остальное.
Склеивая множество таких сетей, мы можем получить сколько угодно башен, и аппроксимировать произвольную функцию трёх переменных. Та же идея работает в m измерений. Меняется только выходное смещение (−m+1/2)h, чтобы правильно втиснуть нужные значения и убрать плато.
Хорошо, теперь мы знаем, как использовать НС для аппроксимации вещественной функции многих переменных. Что насчёт векторных функций f(x1,…,xm) ∈ Rn? Конечно, такую функцию можно рассматривать, просто как n отдельных вещественных функций f1(x1,…,xm), f2(x1,…,xm), и так далее. А потом мы просто склеиваем все сети вместе. Так что с этим легко разобраться.
Задача
- Мы увидели, как использовать нейросети с двумя скрытыми слоями для аппроксимации произвольной функции. Можете ли вы доказать, что это возможно делать с одним скрытым слоем? Подсказка – попробуйте работать с всего двумя выходными переменными, и показать, что: (a) возможно получить функции ступенек не только по осям x или y, но и в произвольном направлении; (b) складывая множество конструкций с шага (a), возможно аппроксимировать функцию круглой, а не прямоугольной башни; © используя круглые башни, возможно аппроксимировать произвольную функцию. Шаг © будет проще сделать, используя материал, представленный в этой главе немного ниже.
Выход за рамки сигмоидных нейронов
Мы доказали, что сеть, состоящая из сигмоидных нейронов, может вычислить любую функцию. Вспомним, что в сигмоидном нейроне входы x1,x2,… превращаются на выходе в σ(∑jwjxj + b), где wj — веса, b – смещение, σ — сигмоида.

Что, если мы рассмотрим другой тип нейрона, использующий другую функцию активации, s(z):

То есть, мы предположим, что если у нейрона на входе будет x1,x2,… веса w1,w2,… и смещение b, то на выходе будет s(∑jwjxj + b).
Мы можем использовать эту функцию активации для получения ступенчатой, точно так же, как в случае с сигмоидой. Попробуйте (в оригинале статьи) на диаграмме задрать вес до, допустим, w=100:


Как и в случае с сигмоидой, из-за этого функция активации сжимается, и в итоге превращается в очень хорошую аппроксимацию ступенчатой функции. Попробуйте поменять смещение, и вы увидите, что мы можем изменить местоположение ступеньки на любое. Поэтому мы можем использовать всё те же трюки, что и ранее, для вычисления любой желаемой функции.
Какие свойства должны быть у s(z), чтобы это сработало? Нам нужно предположить, что s(z) хорошо определена при z→−∞ и z→∞. Эти пределы – это два значения, принимаемых нашей ступенчатой функцией. Нам также нужно предположить, что эти пределы отличаются. Если бы они не отличались, ступеньки бы не получилось, был бы просто плоский график! Но если функция активации s(z) удовлетворяет этим свойствам, основанные на ней нейроны универсально подходят для вычислений.
Задачи
- Ранее в книге мы познакомились с нейроном другого типа — выпрямленным линейным нейроном, или выпрямленной линейной единицей [rectified linear unit, ReLU]. Поясните, почему такие нейроны не удовлетворяют условиям, необходимым для универсальности. Найдите доказательство универсальности, показывающее, что ReLU универсально подходят для вычислений.
- Допустим, мы рассматриваем линейные нейроны, с функцией активации s(z)=z. Поясните, почему линейные нейроны не удовлетворяют условиям универсальности. Покажите, что такие нейроны нельзя использовать для универсальных вычислений.
Исправляем ступенчатую функцию
Покамест мы предполагали, что наши нейроны выдают точные ступенчатые функции. Это неплохое приближение, но лишь приближение. На самом деле существует узкий промежуток отказа, показанный на следующем графике, где функции ведут себя совсем не так, как ступенчатая:

В этом промежутке отказа данное мною объяснение универсальности не работает.
Отказ не такой уж страшный. Задавая достаточно большие входные веса, мы можем делать эти промежутки сколь угодно малыми. Мы можем сделать их гораздо меньшими, чем на графике, невидимыми глазу. Так что, возможно, нам не стоит волноваться из-за этой проблемы.
Тем не менее, хотелось бы иметь некий способ её решения.
Оказывается, её легко решить. Давайте посмотрим на это решение для вычисляющих функции НС со всего одним входом и выходом. Те же идеи сработают и для решения проблемы с большим количеством входов и выходов.
В частности, допустим, мы хотим, чтобы наша сеть вычислила некую функцию f. Как и раньше, мы пытаемся сделать это, проектируя сеть так, чтобы взвешенный выход скрытого слоя нейронов был σ−1⋅f(x):

Если мы будем делать это, используя описанную выше технику, мы заставим скрытые нейроны выдать последовательность функций выступов:

Я, конечно, преувеличил размер промежутков отказа, чтобы их было легче увидеть. Должно быть ясно, что если мы сложим все эти функции выступов, то получим достаточно хорошую аппроксимацию σ−1⋅f(x) везде, кроме промежутков отказа.
Но, допустим, что вместо использования только что описанной аппроксимации, мы используем набор скрытых нейронов для вычисления аппроксимации половины нашей изначальной целевой функции, то есть, σ−1⋅f(x)/2. Конечно, это будет выглядеть, просто как масштабированная версия последнего графика:

И, допустим, мы заставим ещё один набор скрытых нейронов вычислять приближение к σ−1⋅f(x)/2, однако у него основания выступов будут сдвинуты на половину их ширины:

Теперь у нас есть два разных приближения для σ−1⋅f(x)/2. Если мы сложим две этих аппроксимации, то получим общее приближение к σ−1⋅f(x). У этого общего приближения всё равно будут неточности в небольших промежутках. Но проблема будет меньше, чем раньше – ведь точки, попадающие в промежутки отказа первой аппроксимации, не попадут в промежутки отказа второй аппроксимации. Поэтому аппроксимация в этих промежутках окажется примерно в 2 раза лучше.
Мы можем улучшить ситуацию, добавив большое количество, M, накладывающихся аппроксимаций функции σ−1⋅f(x)/M. Если все промежутки отказа у них будут достаточно узкими, любая тока будет находиться лишь в одном из них. Если использовать достаточно большое количество накладывающихся аппроксимаций M, в итоге получится прекрасное общее приближение.
Заключение
Рассмотренное здесь объяснение универсальности определённо нельзя назвать практическим описанием того, как подсчитывать функции при помощи нейросетей! В этом смысле оно больше похоже на доказательство универсальности логических вентилей NAND и прочего. Поэтому я в основном пытался сделать так, чтобы эта конструкция была ясной, и ей было просто следовать, не оптимизируя её детали. Однако попытки оптимизировать эту конструкцию могут стать для вас интересным и поучительным упражнением.
Хотя полученный результат нельзя напрямую использовать для создания НС, он важен, поскольку он снимает вопрос вычислимости какой-либо определённой функции при помощи НС. Ответ на такой вопрос всегда будет положительным. Поэтому правильно спрашивать не вычислима ли какая-либо функция, а каков правильный способ её вычисления.
Разработанная нами универсальная конструкция использует всего два скрытых слоя для вычисления произвольной функции. Как мы обсуждали, возможно получить тот же результат при помощи единственного скрытого слоя. Учитывая это, вы можете задуматься, зачем вообще нам нужны глубокие сети, то есть, сети с большим количеством скрытых слоёв. Не можем ли мы просто заменить эти сети на неглубокие, имеющие один скрытый слой?
Хотя, в принципе, это возможно, существуют хорошие практические причины для использования глубоких нейросетей. Как описано в главе 1, у глубоких НС есть иерархическая структура, позволяющая им хорошо адаптироваться для изучения иерархических знаний, которые оказываются полезными для решения реальных проблем. Более конкретно, при решении таких задач, как распознавание образов, полезно бывает использовать систему, понимающую не только отдельные пиксели, но и всё более сложные концепции: от границ до простых геометрических фигур, и далее, вплоть до сложных сцен с участием нескольких объектов. В более поздних главах мы увидим свидетельства, говорящие в пользу того, что глубокие НС смогут лучше неглубоких справиться с изучением подобных иерархий знания. Подытоживая: универсальность говорит нам, что НС могут подсчитать любую функцию; эмпирические свидетельства говорят о том, что глубокие НС лучше адаптированы к изучениям функций, полезных для решения многих задач реального мира.




