Нейросети в исследовании процессов

Нейронные сети – это статистические вычислительные модели, применяемые к множеству практических задач, в том числе обработка изображений, машинный перевод и поиск шаблонов. При обучении с учителем, нейросеть тренируется на примере уже известных объектов, то есть для всех исходных данных у нас есть предопределенный правильный ответ. Главная идея обучения нейросети – это настроить такую конфигурацию, при которой ответы модели будут максимально приближены к корректным. Что же до рекуррентных нейросетей, то они не только обучаются на исходных объектах, но и предоставляют контекст для каждого следующего предсказания. Это помогает нейросети сохранять состояние, в котором было принято решение. В этой статье мы обсудим применение рекуррентных нейросетей (РНС) в проблеме исследования процесса в process mining.

Задача исследования процесса состоит в получении модели, которая будет отражать поведение, заложенное в исходных данных. Так как это похоже на задачу распознавания шаблонов, то в этой статье мы сфокусируемся на решении задачи исследования процесса с использованием рекуррентных нейросетей. Касательно лога событий в качестве обучающих данных, для каждого события в логе мы будем тренировать нашу нейросеть предсказывать следующее событие. Наша конечная цель извлечь систему переходов, которая представляет собой модель процесса, представленного в логе событий.

Для прояснения подхода возьмём лог событий L = [(a, b, c, d, e), (a, b, d)] в качестве примера. Внутренние вычисления нейросети требуют предобработку последовательностей событий следующим образом:

1.      Добавим два зарезервированных токена «$» и «#» в каждую последовательность указывающих на начало и конец последовательности соответственно

2.      Дополним все последовательности символом «#», чтобы они имели одинаковую длину

Таким образом L преобразуется в L ̃ = [($, a, b, c, d, e, #), ($, a, b, d, #, #, #)] с последовательностями одинаковой длины в 7 символов. Также закодируем имеющиеся токены целыми числами от 0 до |Ʌ|+1 (где |Ʌ| - мощность множества входящих токенов)

Предобработка лога событий загруженного в pandas.DataFrame
def preprocessing(df):    
    tracks = [list(track.sort_values(by=["timest"], ascending=True).activity.values) for track_id, track in df.groupby(df.trace)]    
    tokens = sorted(list(set(df.activity)) +['#'])
    token_to_id = {t:i for i,t in enumerate(tokens)}
    id_to_token = {i:t for i,t in enumerate(tokens)}
    MAX_LEN = max(list(map(len, tracks)))
    tracks_ix = list(map(lambda track: list(map(token_to_id.get,track)), tracks))
    for i in range(len(tracks_ix)):
        if len(tracks_ix[i]) < MAX_LEN:
            tracks_ix[i] += [token_to_id['#']]*(MAX_LEN - len(tracks_ix[i]))
    tracks_ix = np.array(tracks_ix)
    return tokens, tracks_ix, id_to_token, token_to_id
tokens, tracks_ix, id_to_token, token_to_id = preprocessing(df)    

Для построения желаемой системы переходов мы создадим нейросеть способную генерировать последовательности из входящего лога событий. На каждом шаге нейросеть предсказывает вероятности следующих возможных токенов и выбирает наиболее вероятный токен. Интерпретация проблемы предсказания токенов, как задачи классификации позволяет нам использовать специфические методы и архитектуры, доказавшие свою эффективность. Для каждого токена (события) ai мы хотим определить класс последующего токена ai+1, то есть активность, представленную им. Более того, мы должны принять во внимание историю последовательности, иначе прогноз будет зависеть только от предыдущего токена, что приведет к построению графа отношений между индивидуальными событиями. Вот почему присутствует повторяющееся соединение, формирующее более сложный входной вектор. Если нейросеть способна генерировать правдоподобные последовательности, то внутреннее состояние, из которого получен прогноз, вероятно и представляет историю последовательности и текущий токен и может использоваться как состояние в системе переходов. Для решения этой задачи используем нейросеть следующей архитектуры:

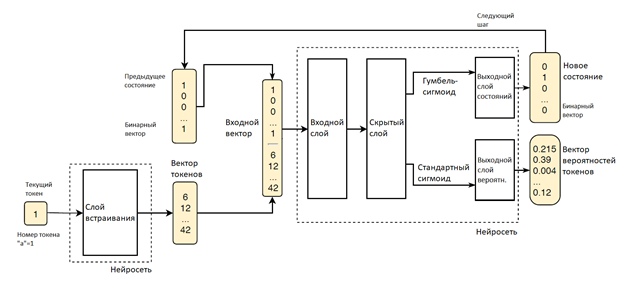
В слое встраивания целое, кодирующее следующий токен из последовательности, трансформируется в вектор токена. Входной вектор для нейросети это соединение двух векторов: бинарного вектора, представляющего предыдущее состояние нейросети и вектор токенов. Далее входной вектор отправляется в скрытый слой, где к вектору применяется линейная трансформация. После этого различные функции активации применяются к вычисленному вектору для извлечения двух различных объектов в выходном слое. Первый – это новый дискретный бинарный вектор, интерпретирующий новое состояние РНС и используемый в качестве параметра для следующей итерации. Для его вычисления мы используем Гумбель-сигмоиду, как доказавшую свою эффективность при аппроксимации дискретных значений. Второй – вектор вероятностей токенов (Таблица 1). Для него мы используем стандартную сигмоиду, так как ее значения относятся к отрезку [0;1].

Таблица 1. Вероятности токенов для первой последовательности лога ~L

sequence = T.matrix('token sequence','int64')

Настрока архитектуры нейросети:
def model(tokens, token_to_id, neurons_num=5):
    sequence = T.matrix('token sequence','int64')
    inputs = sequence[:,:-1] # по символу предсказываю следующий, поэтому входные - все, кроме последнего
    targets = sequence[:,1:] # а выходные - все, кроме первого
    l_input_sequence = InputLayer(shape=(None, None),input_var=inputs)
    tau = theano.shared(np.float32(0.1))
    pseudo_sigmoid = GumbelSigmoid(t=tau)
    class step:    
        #inputs
        h_prev = InputLayer((None, neurons_num),name='previous rnn state')
        inp = InputLayer((None,),name='current character')
        emb = EmbeddingLayer(inp, len(tokens), 30, name='emb') # сопоставление при условии минимума фции потерь
        
        #recurrent part                 
        f_dense = DenseLayer(concat([h_prev, emb]), num_units=8, nonlinearity=T.nnet.relu)    # 0 .. +inf
        s_dense = DenseLayer(f_dense, num_units=neurons_num, nonlinearity=None) # -inf .. +inf
        
        next_state_probs = NonlinearityLayer(s_dense, T.nnet.sigmoid) # Вероятность битов состояния
        h_new = NonlinearityLayer(s_dense, pseudo_sigmoid) # Новое состояние - вектор битов

        next_token_probas = DenseLayer(s_dense, len(tokens),nonlinearity=T.nnet.softmax) # Вероятность токена - P(Ti|Ti-1....T0)
    batch_size = sequence.shape[0]
    initial_state = InputLayer((None, neurons_num), T.zeros((batch_size, neurons_num)))
    training_loop = Recurrence(
        state_variables={step.h_new:step.h_prev},
        state_init={step.h_new:initial_state},
        input_sequences={step.inp:l_input_sequence},
        tracked_outputs=[step.next_token_probas,],
        unroll_scan=False,
    )  
    weights = lasagne.layers.get_all_params(training_loop, trainable=True)    
    predicted_probabilities = lasagne.layers.get_output(training_loop[step.next_token_probas])
    xent = lasagne.objectives.categorical_crossentropy(predicted_probabilities.reshape((-1,len(tokens))),
                                                   targets.reshape((-1,))).reshape(targets.shape)
    mask = T.neq(inputs, token_to_id["#"]) # оставляем только значимые токены, т.к. незначимые появились после паддинга
    loss = (mask * xent).sum(axis=1).mean() # функция ошибки

    #<Loss function - a simple categorical crossentropy will do, maybe add some regularizer>
    updates = lasagne.updates.adam(loss, weights)
    train_step = theano.function([sequence], loss,
                             updates=training_loop.get_automatic_updates()+updates)
    
    h_deterministic = NonlinearityLayer(step.next_state_probs, lambda x: T.gt(x, 0.5).astype(x.dtype))
    validation_loop = Recurrence(
        state_variables={h_deterministic:step.h_prev},
        state_init={h_deterministic:initial_state},
        input_sequences={step.inp:l_input_sequence},
        tracked_outputs=[step.next_token_probas,],
        unroll_scan=False,
    )
    states_seq = get_output(validation_loop[h_deterministic], {l_input_sequence:sequence})
    infer_states = theano.function([sequence], states_seq, updates=None)
    return train_step, infer_states

Мы используем вектор вероятностей токенов для вычисления нашей функции потерь следующим образом. Построим m x r матрицу потерь (кросс-энтропии), где m – количество последовательностей в входном логе, а r – максимальная длина предобработанной последовательности. Каждая строка матрицы относится к последовательности лога, каждый элемент относится к токену (событию) в последовательности. На каждом шаге элемент вычисляется как кросс-энтропия H(y^i, yi), где y^i предсказанная вероятность токена, а yi – реальная.

Так как после предобработки у нас есть излишние символы, которые мы не хотим использовать для обучения нашей модели, мы должны отбросить некоторые ячейки, умножив вычисленную матрицу потерь на маскирующую матрицу. Маскирующая матрица – это матрица с единицами в ячейках с реальными и «$» токенами и нулями в ячейках с «#» токенами. Таким образом умножение оставляет только необходимые значения кросс-энтропии. В итоге функция потерь вычисляется как среднее от сумм по каждой строке (Таблица 2)

Таблица 2. Матрица кросс-энтропии лога ~L

Обучение представляет собой направление нашего лога событий нейросети последовательность за последовательностью и минимизация функции потерь, описанной выше методом стохастического градиентного спуска.

Обучение нейросети:
def training(tokens, tracks_ix, token_to_id, neurons_num=5, n_epochs = 25, batches_per_epoch = 250, batch_size= 10):
    train_step, infer_states = model(tokens,token_to_id)    
    for epoch in range(n_epochs):
        avg_cost = 0;
        for _ in range(batches_per_epoch):
            avg_cost += train_step(sample_batch(tracks_ix, batch_size))
        print("\n\nEpoch {} average loss = {}".format(epoch, avg_cost / batches_per_epoch))
    return infer_states
infer_states = training(tokens, tracks_ix, token_to_id, 10)

Итоговая система переходов (TS) формируется исходя из состояний рекуррентной нейросети, представляющих собой входящий вектор для РНС и новый входящий токен из исходной последовательности и образующих состояния TS. Эти состояния соединяются переходами, определяющимися по исходному токену.

Построение TS:
def build_json(filename, inferred_states, tracks_ix, neurons_num=10): 
    graph = {"states":set(), "transitions":list(), "meta":{"isAccepting":set()}}
    all_states = []
    all_used_states = set()    

    for binary_states in inferred_states:
        binary_states = np.vstack((np.zeros(neurons_num), binary_states)) # add initial state
        states = list(map(binary_state_to_id, binary_states))
        graph["states"].update(set(states))
        all_states.append(states)    
    
    for states, track_ids in zip(all_states, tracks_ix):
        track = list(map(id_to_token.get, track_ids))
        for index, symbol in enumerate(track):
            transition = {"from":states[index], "to":states[index + 1], "track":symbol}
            all_used_states.add(transition["from"])
            all_used_states.add(transition["to"])
            if transition not in graph["transitions"]:
                graph["transitions"].append(transition)  
        graph["meta"]["isAccepting"].add(states[len(track)])
        
    graph["states"] = list(all_used_states)
    graph["meta"]["isAccepting"] = list(graph["meta"]["isAccepting"])
    graph["meta"]["tracksNum"] = len(tracks_ix)
    with open(filename, "w") as json_file:
        json.dump(graph, json_file)
    return graph
inferred_states = infer_states(tracks_ix)
graph = build_json(json_filename, inferred_states, tracks_ix)

Отрисовка графа:
def build_dot(json_graph, filename):
    graph = "digraph test {\n"
    for state in json_graph["states"]:
        if state in json_graph["meta"]["isAccepting"]:
            graph += "\t" + state + " [shape=doublecircle];\n"
        else:
            graph += "\t" + state + ";\n"
    for transition in json_graph["transitions"]:
        graph += "\t" + transition["from"] + " -> " + transition["to"] 
        graph += " [label=\"" + transition["track"] + "\"];\n"
    graph += "}" 
    
    with open(filename, "w") as graph_file:
        print(graph, file=graph_file, end="")
    return graph
dot_graph = build_dot(graph, dot_filename)

В этой работе мы смогли применить нейросети для моделирования процесса на основе лога событий. Полученные результаты дают основу для дальнейших исследований, а также могут применяться в задаче прогнозирования следующего события процесса на основе уже произошедших.

Ссылка на GitHub