Есть такой загадочный факт о линейных преобразованиях: некоторые из них, а именно неоднородное масштабирование и сдвиг, по какой-то причине различают "обычные" векторы и нормали. Когда мы преобразуем "обычный" вектор матрицей, то нормали почему-то нужно преобразовывать обратной транспонированной матрицей. Как это понять?

С помощью нехитрых выкладок можно убедиться, что обратная транспонированная матрица сохраняет перпендикулярность нормалей к своим касательным плоскостям. В какой-то степени этого доказательства достаточно, но оно упускает более глубокую и интересную историю о стоящей за всем этим геометрии. Эту историю я и хочу поведать в нескольких следующих статьях.

Единицы и масштабирование

Вот небольшая затравка, прежде чем мы закопаемся в самую суть статьи. Рассмотрим старое доброе однородное масштабирование (один коэффициент по всем осям). Трудно придумать более безобидное преобразование — это всего лишь умножение всех векторов на одно и то же число.

Но при ближайшем рассмотрении здесь происходит нечто не совсем тривиальное. Некоторые величины несут с собой физические "размерности" или "единицы", такие как длины, площади и объёмы. При масштабировании эти величины изменяются в соответствии со своими единицами. Некоторые значения вообще "безразмерны" и не меняются при масштабировании.

В качестве примера давайте перечислим всевозможные поведения при масштабировании в трёхмерном пространстве. Обозначим масштабный множитель как $$. Тогда:

• Безразмерные числа не меняются, иными словами они умножаются на $$.
• Длины умножаются на $$.
• Площади умножаются на $$.
• Объёмы умножаются на $$.
  Но это ещё не всё: есть так же плотности, которые изменяются как обратные к масштабному коэффициенту величины:
• Линейные плотности умножаются на $$.
• Плотности по площади умножаются на $$.
• Объёмные плотности умножаются на $$.
  Плотности могут выражать вещи вроде количества текселей на длину, или геометрической вероятности, или количества частиц в объёме. Если 3D-модель масштабируется в сторону увеличения, а размер текстуры не изменяется, тогда плотность текселей на ней уменьшается, и так далее.

Получается, даже ограничившись однородным масштабом и рассмотрев скалярные (не векторные) значения, мы уже наблюдаем феномен: различные значения, которые выглядят структурно одинаковыми (все они являются скалярами), оказывается ведут себя по разному будучи преобразованными, из-за различных единиц которые они несут в себе. А именно, они соответствуют различным степеням длины от -3 до 3. Величина, соответствующая $$ степеням длины, масштабируется как $$.

(Можно было бы придумать величины со степенями масштабирования $$ и более, или даже с дробными стпенями. Но оставим их за рамками рассмотрения, потому что у них нет хорошей геометрической интерпретации в 3D.)

Окей, может это чем-то и похоже на различие обычных векторов и нормалей. Но как это работает для векторных величин? Как на всю эту картину влияет неоднородное масштабирование? И где тут появляется обратное транспонирование? Чтобы понять это по-настоящему, нам придётся ещё дальше продвинуться в математику.

Внешние алгебры

Отныне и до конца нам понадобятся внешние алгебры, или алгебры Грассмана. Так как с ними скорее всего знакомы не все читатели, я изложу краткое введение в тему. Для более глубокого понимания обратитесь к этой лекции Эрика Лэнгиела, или к нескольким первым главам книги Дорста Geometric Algebra for Computer Science. В сети есть великое множество других материалов.

Внешняя алгебра — это расширение линейной алгебры, которое действует не только над векторами, но и над некими геометрическими сущностями высших порядков, которые называются бивекторами, тривекторами и так далее. В общем случае эти объекты называются $$-векторы, где $$ — внешняя степень или размерность объекта. Они подчиняются тем же правилам, что и векторы — их можно складывать и умножать на скаляры. Но геометрический смысл у них другой.

Мы часто представляем себе вектор как абстрактную стрелку — у неё есть направление в пространстве (в котором указывает стрелка) и абсолютная величина, представляемая длиной стрелки. Бивектор во многом такой же, но он плоский, а не линейный. Он представляется не стрелкой, а абстрактным участком плоской поверхности.

Как и у векторов, у бивекторов тоже есть направление в том смысле, что плоскость может быть обращена к различным направлениям в пространстве. Ещё у них есть абсолютная величина, геометрически представимая как площадь участка плоскости. Чего у них нет, так это концепции формы на плоскости. Визуализируя бивектор как часть плоскости, вы можете представлять его как квадрат, круг, параллелограмм или любую другую сколь угодно замысловатую фигуру соответствующей площади.

Аналогично, тривекторы — это трёхмерные векторные величины, представляющие участок пространства, а не плоскости или стрелку. Опять же, у них определённой формы, а есть только абсолютное значение, которое теперь является объёмом, а не площадью или длиной.

В трёхмерном пространстве у тривекторов нет направления в полезном смысле слова. Иными словами, у них есть единственное возможное направление, которое параллельно пространству. Тем не менее, у тривекторов есть два противоположных направления, которые мы можем назвать "положительным" и "отрицательным", или "правосторонним" и "левосторонним". Это похоже на то, как вектор может указывать влево или вправо на одномерной прямой, и при желании мы можем назвать эти направления положительным и отрицательным.

В пространствах бо́льших размерностей тривекторы так же могут иметь много разных направлений, как векторы и бивекторы. Кроме того, там могут быть квадвекторы и более высокие степени. Нам же будет достаточно трёх измерений.

Базисные $$-векторы

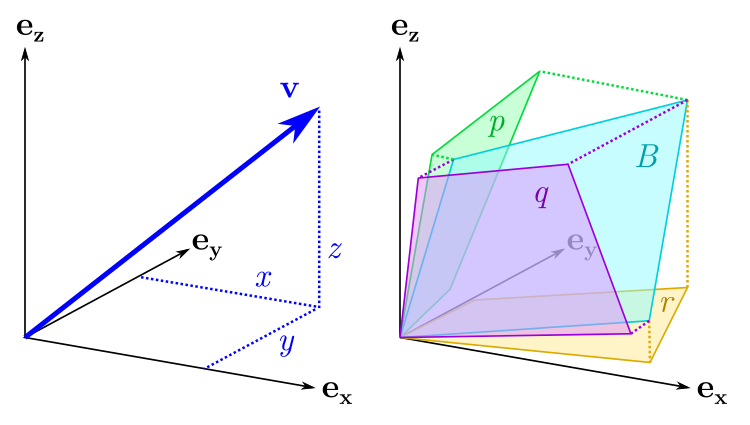
Бивекторы и тривекторы можно разложить на компоненты в базисе, так же как это делается с обычными векторами. Координатная запись вектора $$, $$, означает, что $$ может быть представлен как линейная комбинация базисных векторов:

Базисные векторы $$, $$, $$ определяют направление и масштаб осей $$, $$, $$. Точно так же бивектор $$ можно представить линейной комбинацией базисных бивекторов:

Здесь $$ — это бивектор единичной площади, ориентированный вдоль плоскости $$. $$ и $$ можно представить по аналогии. Базисные бивекторы соответствуют не осям координат, а плоскостям, натянутым на пары осей. Так определяются "координаты бивектора" $$, с помощью которых мы можем обозначить или соорудить любой бивектор в пространстве.

Случай тривектора менее интересен:

Как мы заметили выше, у тривектора в 3D есть только одно возможное направление, потому у них только один базисный элемент: единичный тривектор "вдоль пространства $$. Все остальные тривекторы — это произведения $$ на скаляр.

Внешнее произведение

Итак, внешняя алгебра содержит различные векторообразные объекты разных степеней: обычные векторы (степень 1), бивекторы (степень 2) и тривекторы (степень 3). Скалярам можно приписать степень 0. Наконец, чтобы объекты разных степеней могли взаимодействовать, внешняя алгебра определяет операцию под названием внешнее произведение, обозначаемое через $$. Оно даёт возможность сконструировать бивектор умножая два вектора, например:

В общем случае можно перемножить два любых вектора и получить бивектор, лежащий в плоскости, определяемой этими векторами. Абсолютным значением бивектора будет площадь параллелограмма, построенного на этих векторах (как у векторного произведения).

Заметим, что бивектор не "запоминает" на каких конкретно двух векторах он построен. Любые два вектора в той же плоскости, определяющие параллелограмм той же плоскости и ориентации, породят такой же бивектор. Бивектор может быть разложен на векторы, но не единственным способом.

Так же можно перемножить три вектора, или бивектор с вектором, чтобы получить тривектор.

Такое произведение равнозначно "скалярному смешанному произведению", которое даёт тривектор, представляющий ориентированный объём параллелепипеда, натянутого на три вектора.

Внешнее произведение подчиняется большинству известных правил умножения, например ассоциативности и дистрибутивному закону. Скалярное умножение с ним тоже сочетается. Для скаляра $$ получаем:

Но внешнее произведение двух векторов антикоммутативно, снова как и векторное произведение. Для векторов $$ имеем:

Из этого следует несколько выводов. Во-первых, внешнее произведение любого вектора на себя равно нулю: $$. Более того, внешнее произведение набора линейно-зависимых векторов тоже равно нулю. Например, $$ когда $$ и $$ коллинеарны. В случае трёх векторов, $$ когда $$ копланарны.

Это так же объясняет почему степени выше 3 не существуют в трёхмерном пространстве. Внешнее произведение четырёх трёхмерных векторов всегда равно нулю, потому что в трёхмерном пространстве не может быть четырёх линейно независимых векторов.

Преобразования $$-векторов

Ранее я заявлял, что абсолютное значение вектора можно представлять как длину, значение бивектора — как площадь, а тривектора — как объём. Но что управляет именно таким сопоставлением единиц величинам?

Выше мы видели, что длины, площади и объёмы ведут себя по-разному при масштабировании. Равномерное масштабирование трёхмерного пространства с коэффициентом $$ отмасштабирует длины, площади и объёмы как $$ соответственно. Теперь у нас есть аппарат, показывающий что векторы, бивекторы и тривекторы ведут себя точно так же.

К вектору можно применить масштаб, умножив его на подходящую матрицу:

Вектор $$ как единое целое, его компоненты $$, и его скалярное абсолютное значение, умножаются на коэффициент $$ при масштабировании, поэтому мы может назвать его длиной, и в этом не будет противоречия.

Что насчёт бивекторов? Чтобы увидеть как они ведут себя при масштабировании (или любом другом линейном преобразовании), обратимся к внешнему произведению. В трёхмерном пространстве любой бивектор можно разложить на внешнее произведение двух векторов. Мы умеем преобразовывать векторы, а значит можем преобразовать бивектор, преобразовав составляющие его векторы и взяв внешнее произведение результатов:

Во как! Так как бивектор состоит из двух сомножителей, каждый из которых масштабируется на $$, бивектор обретает коэффициент $$, который делает его площадью.

Тривекторы тоже можно преобразовать, раскладывая на векторы. Теперь неудивительно, что три вектор-сомножителя придают тривектору коэффициент $$. Приведём выкладки для полноты:

Бивекторы и неравномерный масштаб

Теперь наконец мы можем вернуться к исходному вопросу. Что усложнится, если мы применим неравномерное масштабирование?

Чтобы понять это, давайте рассмотрим пример. Будем масштабировать в 3 раза по оси $$, оставляя остальные оси неизменными. Получится матрица вида:

На обычных векторах её действие очевидно: компонента $$ умножается на 3, а компоненты $$ не изменяются. В общем случае матрица изменяет как длину, так и направление вектора в зависимости от изначального направления: векторы, близкие к оси $$ растягиваются сильнее, а близкие к плоскости $$ — слабее.

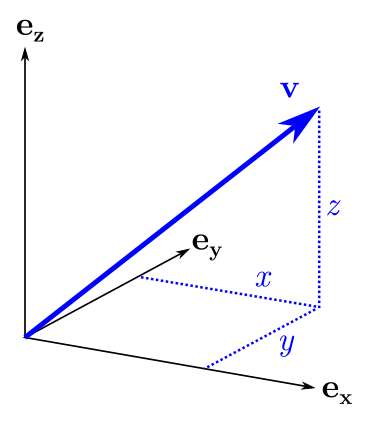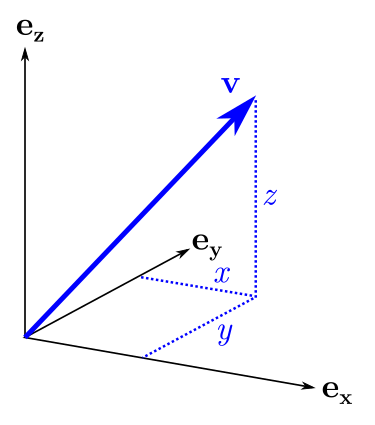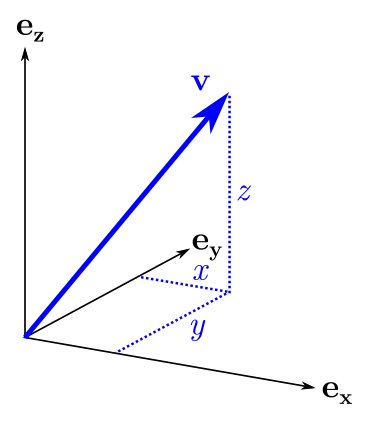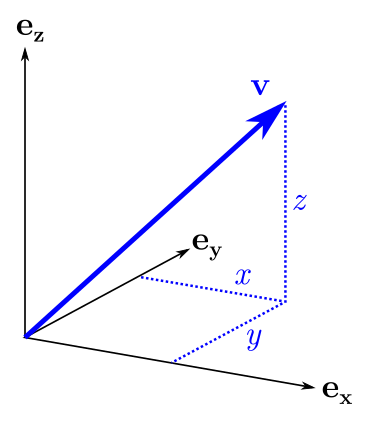
Как токое преобразование повлияет на бивектор? Для начала давайте зайдём со стороны геометрии. Бивектор обозначает участок плоскости с заданными площадью и направлением, в которое направлена "лицевая" сторона. При растяжении такого участка вдоль оси $$ мы ожидаем, что и направление и площадь изменятся. Но различные бивекторы изменятся по разному: на бивектор, близкий к плоскости $$, растяжение повлияет меньше, а бивектор, чья плоскость близка к $$, будет растянут сильнее.

Окей, вернёмся к алгебре. Как было показано выше, любой бивектор можно разложить на базисные бивекторы, выровненные по осям:

Чтобы применить масштабирование $$ к бивектору, нужно лишь применить его к базисным бивекторам. Для этого разложим их на базисные векторы и применим $$ к ним:

Это соответствует геометрической интуиции: $$ не изменился, а $$ и $$ обрели множетель 3, потому что их плоскости включают ось $$.

Таким образом, вот общий эффект применения $$ к бивектору $$:

Теперь, как и в случае с вектором, можно выписать преобразование бивектора $$ в виде компонент, к котором применяется матрица:

Это то же самое преобразование, которое мы только что вывели, записанное в другой нотации. Обратите внимание на одно различие: матрица в этом выражении не совпадает с матрицей $$ исходного преобразования.

Заметим однако забавное совпадение: обратная транспонированная $$ пропорциональная матрице из предыдущей формулы:

К чему бы это?

Присоединённая матрица

Фактически, матрица преобразования для бивектора — это присоединённая матрица к $$.

Она пропорциональна обратной транспонированной матрице с коэффициентом $$. (Обратную к $$ матрицу можно получить транспонированием присоёдинённой матрицы, разделив её на $$). Присоединённая матрица определена даже когда $$ необратима. Это хорошее свойство, потому что мы можем преобразовывать вектор необратимой матрицей, и должна быть возможность проделать то же самое с бивектором!

Давайте получше поймём почему присоединённая матрица — это то, что нужно. Введём понятие алгебраического дополнения.

У каждого элемента квадратной матрицы $$ есть алгебраическое дополнение. Вычисляется алгебраическое дополнение элемента на $$-ой строке и $$-ом столбце следующим образом:

1. Возьмём исходную матрицу $$ и вычеркнем строку $$ и столбец $$. Останется подматрица размером $$.
2. Вычислим определитель этой подматрицы.
3. Умножим определитель на $$, то есть изменим его знак если $$ нечётно. Это и есть алгебраическое дополнение!

Теперь склеим алгебраические дополнения обратно в матрицу $$, в результате чего получится присоединённая матрица.

Но как так получилось, что эта кнострукция работает в преобразовании бивектора? Посмотрим на первый компонент бивектора $$. Этот член представляет компонент плоскости $$, а потому на него влияют только преобразования, которые $$ применяет к осям $$ и $$. В рецепте приготовления алгебраического дополнения $$ матрицы $$ тоже использзуется подматрица $$, которая определяет что $$ делает с осями $$ и $$. Далее мы берём её определитель, который есть ни что иное, как коэффициент масштабирования плоскости $$!

Из-за того, что мы выбрали бивекторный базис $$ именно в таком порядке, каждый элемент присоединённой матрицы автоматически вычисляет детерминант, который определяет как $$ масштабирует площади в соответствующей плоскости. Или, для внедиагональных элементов, как $$ отображает площади из одной координатной плоскости в другую. Другими словами, алгебраические дополнения оказались в точности теми коэффициентами, которыми преобразуются компоненты бивектора.

(Между почим, знаковый множитель с третьего шага нужен чтобы разрешить некоторые проблемы упорадоченности. Без него у нас был бы базисный элемент $$ вместо $$. Последний базисный элемент предпочитается по общепринятому соглашению.)

Несмотря на сфокусированность нашего повествования на трёхмерном случае, замечу, что в размерности $$ присоединённая матрица преобразует $$-векторы в подходящем базисе. Фактически, для преобразования $$-векторов понадобится матрица $$-ых миноров, то есть определителей подматрицы с вычеркнутыми $$ строками и столбцами.

Бивекторы и нормали

В этом месте я должен сделать небольшое признание. На протяжении последних нескольких абзацев я прятал кое что в рукаве. Трюк вот в чём: бивекторы изоморфны обычным векторам в 3D. Фактически, компоненты $$ бивектора в стандартном базисе — это компоненты нормали $$ к плоскости бивектора с точностью до нормализации!

Давайте посмотрим как так получается. Ранее мы видели, что внешнее произведение набора линейно зависимых векторов равно нулю. Это значит, что плоскость бивектора $$ может быть задана уравнением:

Любой вектор $$, лежащий в плоскости бивектора $$ удовлетворяет этому уравнению потому что он образует линейно зависимый набор с двумя векторами, на которые натянута плоскость. Или, с другой стороны, тривектор, образованный $$ и $$ будет иметь нулевой объём.

Разложим это уравнение в стандартных векторном и бивекторном базисах и упростим:

Поясню на случай если шаги не очень понятны. Во второй строке я распределил внешнее произведение по всем членам базиса, большинство из которых уничтожились, потому что в них во внешнем произведении участвовало по две копии одной оси (например, $$). В третьей строке я перегруппировал оси всех тривекторов к единому виду $$, что вполне законно, если мы отслеживаем изменения знака. Здесь во всех случаях было чётное количество изменений знака. Наконец, я вынес $$ и сократил на него.

Теперь последняя строка выглядит как скалярное произведение векторов $$ и $$! Другими словами, она выглядит как обычное уравнение плоскости $$ с вектором нормали $$.

Отсюда видно, что бивекторные координаты $$ в базисе $$ так же являются координатами нормали к плоскости в стандартном векторном базисе $$. Более того, внешнее произведение вектора на бивектор идентично скалярному произведению на соответствующий вектор нормали. Формально это применение звезды Ходжа, которая в трёхмерном случае взаимозаменяет бивекторы и их нормали. Подробнее об этом поговорим в будущих статьях.

Дальнейшие вопросы

Мы увидели, что векторы нормали в трёхмерном случае можно в какой-то мере представлять себе как бивекторы из внешней алгебры. Так же мы поняли геометрически почему присоединённая матрица — это правильный инструмент для преобразования бивектора. Это отвечает на наш исходный вопрос (почему некоторые преобразования различают обычные векторы и нормали) более удовлетворительно чем "алгебра так устроена".

Тем не менее, от нас ускользнуло ещё несколько вопросов. Я сказал, что бивекторы "изоморфны" векторам нормали, имея ввиду что медлу ними есть соотношение один к одному. Но какое именно соотношение? Вдобавок, почему мы закончили на присоединённой матрице, а не на обратной транспонированной? Они пропорциональны между собой, и обычно на практике не важно какую именно использовать, потому что нам не важны длины нормалей (обычно мы из всё равно нормализуем). Но мне бы всё ещё хотелось понять корни этого несоответствия.

Ещё вопрос: в затравке вначале статьи нам встретились единицы как с положительными, так и с отрицательными степенями масштаба, от -3 до 3. Теперь мы увидели, что внешние $$-векторы масштабируются как стпень $$ от 0 до 3. Но что насчёт векторных единиц с отрицательными степенями масштаба? Существуют ли они? Если да, то что они такое?

В следующей серии мы зароемся ещё глубже и усложним нашу геометрическую историю ещё сильнее.