Очередной заход на Гипотезу Коллатца. Простая арифметика, ориентированные графы и прямая генерация нечётных чисел

0

Мне кажется всем и так понятно что это (кто всё же не знает - вперёд в вики), поэтому попробую просто пройтись по наработкам.

Картинок немного, начинаются с пункта 5. Ближе к концу статьи есть питонный код на случай если хочется быстро посмотреть много чисел. Качество приведённого кода мне самому не нравится. Оно соответствует подходу "у меня есть такие-то затеи и записи, надо быстро запрототипировать и посмотреть результаты", а не является результатом вытачивания готовой задачи по заранее установленным лекалам. Код несёт вспомогательную функцию к статье, основная мысль даётся текстом и формулами.

1

Для начала заметим, что можно спокойно отбрасывать чётные числа - они по определению функции переходят в нечётные.

$1, 2, 3, 4, ... \rightarrow 1, 3, 5, 7, ...$

Также мы можем несколько модифицировать верхнюю ветку функции, заменив на $1.5n + \frac 1 2$ .

Соответственно:

$cltz(n) = \begin{cases} 1.5n + \frac 1 2, & n\equiv 1\pmod 2 \\ n / 2 , & n\equiv 0\pmod 2 \end{cases}$

Далее, актуальная проблема аналогична классической - доказать, что

$cltz^k(n) = 1, \ k \gt 0$

2

Посмотрим, как поведут себя нечётные числа при применении этой функции:

$\begin{align} 1 & \rightarrow & 2 \\ 3 & \rightarrow & 5 \\ 5 & \rightarrow & 8 \\ 7 & \rightarrow & 11 \\ & ... \end{align}$

Чуть модифицируем этот список, указав порядковый номер нечётного числа и пропишем также альтернативную запись получающегося результата, и следующий шаг применения если получаются чётные:

$\begin{align}& [1] & 1 & \rightarrow 1 + 1 & \Rightarrow & \, 2 & \rightarrow 1 \\& [2] & 3 & \rightarrow 3 + 2 & \Rightarrow & \, 5 \\& [3] & 5 & \rightarrow 5 + 3 & \Rightarrow & \ 8 & \Rightarrow 1 \\& [4] & 7 & \rightarrow 7 + 4 & \Rightarrow & \, 11 \\& [5] & 9 & \rightarrow 9 + 5 & \Rightarrow & \, 14 & \rightarrow 7\\& ...\end{align}$

Здесь явно виден следующий паттерн:

$[m_{i}] \, n_{i} \rightarrow n_{i} + m_{i} \Rightarrow n_{i+1}$

Номера чисел в полученном ряду получаются по формуле: $[m] \iff (n + 1) / 2$
Это справедливо также и для чётных чисел, они будут принимать вид , например - $[5.5] \iff 10$ .

Посмотрим как данная система поведёт себя на числе проводя пошаговое применение доводя до единицы. Также будем записывать изменение порядкового номера.

Пошаговая раскадровка действий от числа 25

$\begin{align}& [13] & 25 & \rightarrow 25 + 13 & \Rightarrow & \, 38 \\ \rightarrow + 6.5 & \\ & [19.5] & 38 & \rightarrow /2 & \Rightarrow & \, 19 \\ \rightarrow - 9.5 & \\ & [10] & 19 & \rightarrow 19 + 10 & \Rightarrow & \, 29 \\ \rightarrow + 5 & \\ & [15] & 29 & \rightarrow 29 + 15 & \Rightarrow & \, 44 \\ \rightarrow + 7.5 & \\ & [22.5] & 44 & \rightarrow /2 & \Rightarrow & \, 22 \\ \rightarrow - 11 & \\ & [11.5] & 22 & \rightarrow /2 & \Rightarrow & \, 11 \\ \rightarrow - 5.5 & \\& [6] & 11 & \rightarrow 11 + 6 & \Rightarrow & \, 17 \\ \rightarrow + 3 & \\ & [9] & 17 & \rightarrow 17 + 9 & \Rightarrow & \, 26 \\ \rightarrow + 4.5 & \\ & [13.5] & 26 & \rightarrow /2 & \Rightarrow & \, 13 \\ \rightarrow - 6.5 & \\ & [7] & 13 & \rightarrow 13 + 7 & \Rightarrow & \, 20 \\ \rightarrow + 3.5 & \\ & [10.5] & 20 & \rightarrow /2 & \Rightarrow & \, 10 \\ \rightarrow - 5 & \\ & [5.5] & 10 & \rightarrow /2 & \Rightarrow & \, 5 \\ \rightarrow - 2.5 & \\ & [3] & 5 & \rightarrow 5 + 3 & \Rightarrow & \, 8 \\ \rightarrow + 1.5 & \\ & [4.5] & 8 & \rightarrow /2 & \Rightarrow & \, 4 \\ \rightarrow - 2 & \\ & [2.5] & 4 & \rightarrow /2 & \Rightarrow & \, 2 \\ \rightarrow - 1 & \\ & [1.5] & 2 & \rightarrow /2 & \Rightarrow & \, 1 \\ \rightarrow - 0.5 & \\ & [1] & 1 & . \\ \end{align}$

Здесь мы можем заметить, что ситуация на самом деле не требует самих чисел, достаточно одних лишь порядковых номеров и их изменений.

Те же действия но уже только с порядковыми номерами

$\begin{align} & [13] \\ \rightarrow + 6.5 & \\ & [19.5] \\ & \;\;\;\;\;\; - 9.5 \leftarrow \\ & [10] \\ \rightarrow + 5 & \\ & [15] \\ \rightarrow + 7.5 & \\ & [22.5] \\ & \;\;\;\;\;\; - 11 \leftarrow \\ & [11.5] \\ & \;\;\;\;\;\; - 5.5 \leftarrow \\ & [6] \\ \rightarrow + 3 & \\ & [9] \\ \rightarrow + 4.5 & \\ & [13.5] \\ & \;\;\;\;\;\; - 6.5 \leftarrow \\ & [7] \\ \rightarrow + 3.5 & \\ & [10.5] \\ & \;\;\;\;\;\; - 5 \leftarrow \\ & [5.5] \\ & \;\;\;\;\;\; - 2.5 \leftarrow \\ & [3] \\ \rightarrow + 1.5 & \\ & [4.5] \\ & \;\;\;\;\;\; - 2 \leftarrow \\ & [2.5] \\ & \;\;\;\;\;\; - 1 \leftarrow \\ & [1.5] \\ & \;\;\;\;\;\; - 0.5 \leftarrow \\ & [1]. \end{align}$

3

На основе полученной схемы можно вывести следующие закономерности:

$m_i \equiv 0\pmod 2$ :

$\begin{align} & [m_i] \\ \rightarrow + {\frac {m_i} 2} & \\ & [m_{i-1}] \\ \end{align}$

$\begin{align} & [m_i] \\ & \;\;\;\;\;\; - \frac {m_i - 0.5} 2 \leftarrow \\ & [m_{i-1}] \\ \end{align}$

Здесь $[m_{i+1}]$ может иметь вид как так и просто .

Оба паттерна при этом справедливы как для "движения вниз" по последовательности, так и при "движении наверх" т.е от $[m_{i+1}]$ к $[m_{i}]$ . Выпишем "плюсовые" и "минусовые" действия:

, движение от к $m_{i+1}$ :

$\frac {2m_i} 3 = m_{i+1}$

, движение от к $m_{i+1}$ :

$m_i + m_i - 0.5 = m_{i+1}$

, обратное движение, от $m_{i+1}$ к :

$\frac {3m_i} 2 = m_{i-1}$

, обратное движение, от $m_{i+1}$ к :

$m_i - \frac {m_i - 0.5} 2 = m_{i-1}$

Примеры от 1) к 4),

$\begin{align} \frac {2 * 4.5} 3 & = \ 3 \\ 5.5 + 5.5 - 0.5 & = \ 10.5 \\ \frac {13 * 3} 2 & = \ 19.5 \\ 22.5 - \frac {22.5 - 0.5} 2 & = \ 11.5 \\ \end{align}$

4

Теперь на основе данных операций и номеров можно создать орграф.

Данный граф будет иметь следующие особенности:

Переходы определены для всех и начиная с .

В каждую вершину графа может быть лишь одна точка входа.

Это достигается за счёт невозможности ввести войти в одну вершину одновременно и через "плюсовое" и через "минусовое" движение, что можно проверить через уравнение:

$\begin{align}& \frac {2x_i} 3 & = & \ 2x_j - 0.5 \\ & ... \\& x_i & = & \ 3 x_j - \frac 3 4 \\ & x_j & = & \ \frac {x_i} 3 + \frac 1 4 \\ \end{align}$

И и однако не относятся ни к ни к и соответственно, не принадлежат базовому графу.

В качестве исходной вершины будет положена , т.к она является наименьшей в графе.

Граф содержит единственный цикл между двумя соседними вершинами: $[1] \leftrightarrow [1.5]$ . Для удобства дальнейшего рассмотрения мы можем игнорировать "плюсовой" переход $[1.5] \rightarrow [1]$ , т.к цикл не влияет на последующую структуру графа. Таким образом, будет также единственной вершиной без точки входа.

назад, вперёд:

$\begin{align}& \frac {3x_i} 2 & = & \ 2x_i - 0.5 \\& ... \\& x_i & = & \ 1 \\\end{align}$

вперёд, назад:

$\begin{align}& \frac {2x_j} 3 & = & \ x_j - \frac {x_j - 0.5} 2 \\& ... \\& x_j & = & \ 1.5 \\\end{align}$

При продолжительном движении назад по переходам переходит в . Количество шагов тут будет равным степени двойки в оригинальном числе, например, для 24 потребуется 3 шага.
В случае когда является чётным, то при обратных оно будет двигаться по другим номерам вида пока не достигнет нечётного номера. Количество шагов до достижения нечётного номера аналогично 5) также равно степени двойки, только на этот раз присутствующей в .
Нечётное при обратном переходе отображается в , кроме особого случая , см. 4).

Свойства 5)-7) будут более наглядны при визуальном построении.

Заметим, что данный граф является несбалансированным бинарным деревом.

Соответственно, мы можем пронумеровать его вершины идя по уровням вниз, и считая слева направо. Левая ветка отображает переход, правая - .

Таким образом, мы получаем полное отображение натуральных чисел на структуру .

Здесь же стоит отметить, что уникальными являются как значения вершин графа, так и значения рёбер. Значение вершины однозначно определяет родительскую вершину а также одну или две дочерние вершины, а значение ребра - обе вершины которые оно соединяет.

5

Теперь мы можем визуализировать основной граф с вершинами разложенными по координатной сетке таким образом, что находятся друг над другом в зависимости от кол-ва перехов, а располагаются справа друг к другу в порядке возрастания. располагается в левом нижнем углу изображения.

Выведем граф на момент полного заполнения шага 15 (левые верхние колонки не показывается полностью чтобы не занимать слишком много места, также столбцы справа визуально подвинуты для более понятного внешнего вида):

Помимо всего прочего, отдельно интересно что столбцы с основаниями $[ N ] \equiv 2\pmod 3$ не порождают новых оснований, а лишь растут вверх.

Прометим теперь движение по графу от числа 13 к единице:

От числа 38 к единице:

6

Как можно видеть, структура вполне однозначна: граф по мере заполнения уровней вбирает в себя всё больше чисел, а запуск поиска обратного пути для любого натурального числа единственным образом приводит нас к .

Тем не менее, для соответствия описанной схемы классической Гипотезе Коллатца необходимо чтобы при поиске обратного пути при "плюсовых переходах" был добавлен заход в промежуточную вершину вида .
Для сравнения, на число 13.

Текущий обратный ход:

$\begin{align}& [7] & 13 \\& [10.5] & 20.0 \\& [5.5] & 10.0 \\& [3.0] & 5.0 \\& [4.5] & 8.0 \\& [2.5] & 4.0 \\& [1.5] & 2.0 \\& [1.] & 1 \\\end{align}$

Классическая Гипотеза Коллатца:

$\begin{align}& [7] & 13 \\& [20.5] & 40.0 \\& [10.5] & 20.0 \\& [5.5] & 10.0 \\& [3.0] & 5.0 \\& [8.5] & 16.0 \\& [4.5] & 8.0 \\& [2.5] & 4.0 \\& [1.5] & 2.0 \\& [1.] & 1 \\\end{align}$

Модификация поиска обратного пути выглядит довольно очевидным образом, поэтому мы легко можем подготовить модифицированную версию. Важно отметить, что такая модицикация не затрагивает структуру и свойства графа - это всего лишь функция сбора вершин при поиске обратного пути. Аналогичным образом мы могли бы подставлять не одну промежуточную вершину , а две или более.

Для сравнения посмотрим как изменились отмеченные вершины в случае с числом 13:

Таким образом, можно утверждать эквивалентность данного построения и классической Гипотезы Коллатца.

7

В целом вышеизложенного достаточно чтобы сделать следующие выводы о Гипотезе Коллатца:

Из натуральных чисел единственной исходной точкой может быть только число 1.
Т.к в самом графе отсутствуют циклы кроме $[1.5] \rightarrow [1]$ , а операция противохода от заданного числа однозначно определена как в основной версии, так и в модифицированных, то для любых натуральных чисел Гипотеза Коллатца не может породить циклические переходы чисел.
Условиям достижимости внутри графа соответствуют все натуральные числа. Соответственно, невозможна структура бесконечно возрастающих переходов натуральных чисел не имеющая в своём основании натуральное число принадлежащее графу.

Гипотеза доказана. $_{\blacksquare}$

Почему по-другому так проблемно и тяжело?

Напоследок рассмотрим проблемы иной интерпретации функции противохода по графу, используя для этого построение того же графа но в виде бинарного дерева. Листья с "null" обозначают что данная операция невозможна по условиям построения графа.

Бинарное дерево c поиском числа 18:

Теперь посмотрим на модифицированную версию:

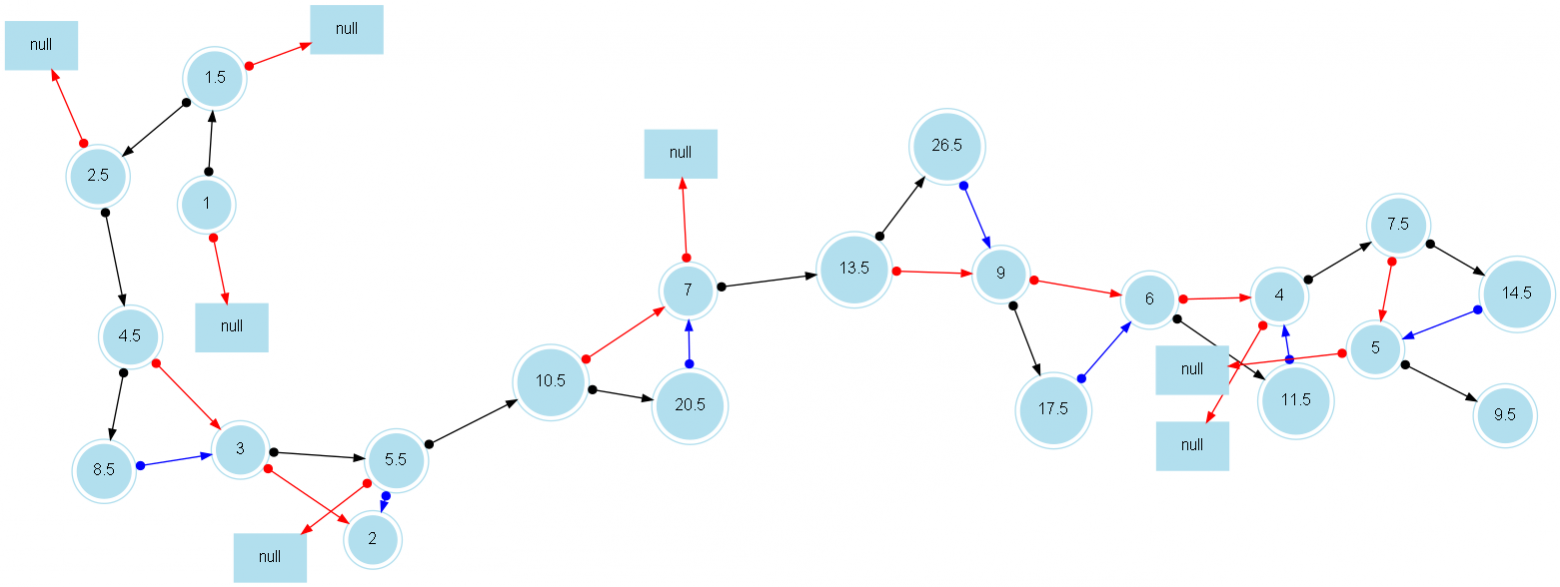
Если снять предположение что дополнительные переходы являются лишь особенностью функции поиска пути, то ацикличность уже требует отдельного доказательства - мы получаем уже структуру где у каждой вершины три выходных пути и 1-2 входных.
Ещё более интересная ситуация случается, если снять запрет на присутствие в графе чисел отличных от натуральных.

Сравним порождающие структуры для окрестностей текущей вершины:

Описанный в данной работе граф:

Eсли вершина не является натуральным числом то она не добавляется. Родительская вершина всего одна и может быть только натуральным числом.

Модифицированный граф позволяющий как несколько входных точек, так и рациональные числа:

Второй случай очевидным образом порождает структуры уже кардинально отличные от первого. Сами функции перехода и их отношения становятся более сложными. Помимо цикличности здесь мы также не можем гарантировать уникальность включения какого-либо числа без отдельного исследования.
Если локально высчитывать для вершины каждой тройки из 1) или центральной вершины из 2), то мы также получим ситуацию где граф сохраняет в себе различные значения являющиеся рациональными дробями.

Любопытной может быть также вариация основного бинарного дерева, где вместо разрешаются номера вида $[ N.\frac 1 3 ]$ и $[ N.\frac 2 3 ]$ .

Немного кода, немного бинарных деревьев

Код скромный и сделан в сугубо демонстративных целях.

Для визуализации тут используется библиотека binarytree, для рендеринга ей требуется также установленный для Питона пакет graphviz.

from binarytree import Node
from decimal import Decimal


def try_right_move(n):
    return Decimal(n) / 3 * 2

def make_left_move(n):
    return Decimal(n)  * 2 - Decimal('0.5')


def translate_from_cltz_ordinal(n):
    return Decimal(n) * 2 - 1



def gen_n_levels_deep(base_ord, n):
    tree = Node(base_ord)
    k = n - 1
    while k > 0:
        nodes_to_try = tree.levels[-1]
        for i in nodes_to_try:
            i.left  = Node(str(make_left_move(Decimal(i.value))))

            # на случай вывода только N-вершин
            #if Decimal(i.value) % 3 != 2:
            #    i.left  = Node(str(make_left_move(Decimal(i.value))))
                
            if str(i.value) != '1.5':
                right_val_cand = try_right_move(Decimal(i.value))
                if str(right_val_cand)[-2:] in ['.5', '.0'] or ( '.' not in str(right_val_cand)):
                    i.right = Node(str(right_val_cand))
        k -= 1
    
    return tree
  
# генерируем дерево от корня '1.0' на 8 шагов вглубину
r = gen_n_levels_deep(str(Decimal('1.0')), 8 )

# отображаем целые числа без нуля-с-точкой на конце
for i in r:
    if i.value[-2:] in ['.0']:
        i.value = i.value[:-2]
        
# на случай вывода только N-вершин
#for i in r:
#    if str(i.value)[-2:] in ['.5']:
#        i.value = ''
  
# на случай когда нужен вывод не порядковых номеров, а самих чисел
#for i in r: i.value = int(translate_from_cltz_ordinal(i.value))

r.graphviz().render(filename="binary_tree.gv", format='png')

Полученное дерево на 8 шагов

Оно же, но с отображением оригинальных чисел

Можно также убрать показ значений вершин и не просчитывать их для вершин с номерами дающими остаток при делении на тройку, т.к начиная с этих вершин не создаются новые вершины с целочисленными номерами.

Вывод только целочисленных вершин на шаге 14

Регулярность расположения вершин указывает на то, что при доработке алгоритма возможно создавать древовидные структуры и на сугубо целочисленных порядковых номерах, что в свою очередь будет являться графом последовательно создающим исключительно нечётные числа по мере их появления в последовательности Коллатца.

Заход на исключительно нечётные числа в последовательности Коллатца

Для начала введём дополнительную типизацию для номеров вида :

$\begin{align} [N] \equiv 0 \pmod 3 & \rightarrow & [ N.\frac 0 3 ] \\ [N] \equiv 1 \pmod 3 & \rightarrow & [ N.\frac 1 3 ] \\ [N] \equiv 2 \pmod 3 & \rightarrow & [ N.\frac 2 3 ] \\ \end{align}$

Наблюдая структуру графа в пункте 5 мы можем заметить, что новые нечётные числа появляются лишь в столбцах чьи порядковые номера отличны от $[ N.\frac 2 3 ]$ .

Далее объявим три случая появления в графе новых нечётных чисел:

1) Число появляется из вершины в столбце роста чёрных чисел начиная с первой такой "генерирующей вершины" находящейся на 1-2 шага выше основания столбца. Если рассматривать все первые "боковые" относительно рассматриваемого столбца вершины с нечётными числами, то переход между ними происходит таким образом:

$4 m_{i} - 1= m_{i+1}$

2) Та самая первая "генерирующая вершина". В данном случае возможны два случая - это вершина находящая сразу над основанием столбца, либо через одну над ним. Появление обоих полностью детерминировано типом основания столбца.

$\begin{align} [ N.\frac 0 3 ] & \rightarrow & \frac {8m_i} 3 - 1 = m_{i+1} \\ [ N.\frac 1 3 ] & \rightarrow & \frac {4m_i - 1} 3 = m_{i+1}\\ \end{align}$

3) Число появляется от самого основания столбца, если порядковый номер последнего имеет вид $[ N.\frac 0 3 ]$ . Осуществляется этот переход по уже известной формуле:

$\frac {2m_i} 3 = m_{i+1}$

Такая структура сохраняет основные свойства оригинала, только в этот раз количество выходных вершин варьируется от до .

Применяя это мы можем построить граф уже сугубо нечётных чисел, в данном случае на 9м шаге алгоритма:

Используемый тут код

import collections
from decimal import Decimal
from typing import Any

from attr import dataclass
from graphviz import Source



def translate_from_cltz_ordinal(n):
    return Decimal(n) * 2 - 1




INTNODE_TYPE   = 'N'
ONETHIRD_TYPE  = 'N.1/3'
TWOTHIRDS_TYPE = 'N.2/3'

def determine_type_of_cltz_node(n):

    if n.cltz_ordinal % 3 == 0:
        return INTNODE_TYPE
    elif n.cltz_ordinal % 3 == 1:
        return ONETHIRD_TYPE
    elif n.cltz_ordinal % 3 == 2:
        return TWOTHIRDS_TYPE



@dataclass
class Cltz_node():

    cltz_ordinal:   int = 1
    actual_value:   int = 1  
    lvl: int = 0 

    cltz_type  :  str = INTNODE_TYPE
    parent_node:           int = None # Cltz_node.cltz_ordinal
    parent_node_cltz_ordinal: int = None # Cltz_node.cltz_ordinal
    parent_node_actual_value: int = None # Cltz_node.cltz_ordinal
    created_by_action:     str = 'first' # first\left\right\center
 
    left_child:    Any = None # Cltz_node.cltz_ordinal
    center_child:  Any = None # Cltz_node.cltz_ordinal
    right_child:   Any = None # Cltz_node.cltz_ordinal
 

    def try_add_child_nodes(self):
        self.try_add_left_child()
        self.try_add_center_child()
        self.try_add_right_child()

    def try_add_left_child(self):

        if self.created_by_action == 'left' or self.cltz_type != TWOTHIRDS_TYPE and self.created_by_action != 'right':

            new_node = Cltz_node(
                cltz_ordinal = self.cltz_ordinal * 4 - 1,
                parent_node_cltz_ordinal = self.cltz_ordinal,
                parent_node_actual_value = self.actual_value,
                created_by_action        = 'left',
                lvl         = self.lvl + 1
            )
            new_node.cltz_type    = determine_type_of_cltz_node(new_node)
            new_node.actual_value = translate_from_cltz_ordinal(new_node.cltz_ordinal)
            self.left_child = new_node


    def try_add_center_child(self):
        if self.cltz_ordinal != 1 and self.cltz_type == INTNODE_TYPE:

            new_node = Cltz_node(
                cltz_ordinal             = int(self.cltz_ordinal * 8 / 3 - 1),
                parent_node_cltz_ordinal = self.cltz_ordinal,
                parent_node_actual_value = self.actual_value,
                created_by_action        = 'center',
                lvl         = self.lvl + 1
            )
            new_node.cltz_type    = determine_type_of_cltz_node(new_node)
            new_node.actual_value = translate_from_cltz_ordinal(new_node.cltz_ordinal)
            self.center_child = new_node

        elif self.cltz_ordinal != 1 and self.cltz_type == ONETHIRD_TYPE:

            new_node = Cltz_node(
                cltz_ordinal             = int( (self.cltz_ordinal * 4 - 1 ) / 3 ),
                parent_node_cltz_ordinal = self.cltz_ordinal,
                parent_node_actual_value = self.actual_value,
                created_by_action        = 'center',
                lvl         = self.lvl + 1
            )
            new_node.cltz_type    = determine_type_of_cltz_node(new_node)
            new_node.actual_value = translate_from_cltz_ordinal(new_node.cltz_ordinal)
            self.center_child = new_node

    def try_add_right_child(self):
        if self.cltz_ordinal != 1 and self.cltz_type == INTNODE_TYPE:

            new_node = Cltz_node(
                cltz_ordinal             = int(self.cltz_ordinal / 3 * 2),
                parent_node_cltz_ordinal = self.cltz_ordinal,
                parent_node_actual_value = self.actual_value,
                created_by_action        = 'right',
                lvl         = self.lvl + 1
            )
            new_node.cltz_type    = determine_type_of_cltz_node(new_node)
            new_node.actual_value = translate_from_cltz_ordinal(new_node.cltz_ordinal)
            self.right_child = new_node

    def get_child_nodes(self):
        ret = []

        if self.left_child:
            ret.append(self.left_child)
        if self.center_child:
            ret.append(self.center_child)
        if self.right_child:
            ret.append(self.right_child)


        return ret

 


def gen_n_levels_deep(n):
    root = Cltz_node(cltz_ordinal=1)

    k = n - 1
    root.try_add_child_nodes()
    nodes_next = root.get_child_nodes()


    while k > 0:
        nodes_to_try = nodes_next
        nodes_next   = []
        for i in nodes_to_try:
            i.try_add_child_nodes()
            for nn in i.get_child_nodes():
                nodes_next.append(nn)
        k -= 1
    return root


def cltz_odd_tree_to_graph(root):
    ans = []

    if root is None: return ans

    queue = collections.deque()
    queue.append(root)

    while queue:
        currSize = len(queue)
        currList = []

        while currSize > 0:
            currNode = queue.popleft()

            if currNode.cltz_ordinal != 1:
                currList.append(f'{currNode.actual_value} [label="{currNode.actual_value}"]\n')

                if currNode.created_by_action == 'left':
                    currList.append(f'{currNode.parent_node_actual_value} -> {currNode.actual_value} \n')
                elif currNode.created_by_action == 'center':
                    currList.append(f'{currNode.parent_node_actual_value} -> {currNode.actual_value} [color="red", arrowhead=normal, dir=both, arrowtail=dot]\n')
                elif currNode.created_by_action == 'right':
                    currList.append(f'{currNode.parent_node_actual_value} -> {currNode.actual_value} [color="blue", arrowhead=normal]\n')
            else:
                currList.append(f'{currNode.actual_value} [label="{currNode.actual_value}", color="darkblue"]\n')

            currSize -= 1

            if currNode.left_child is not None:
                queue.append(currNode.left_child)
            if currNode.center_child is not None:
                queue.append(currNode.center_child)
            if currNode.right_child is not None:
                queue.append(currNode.right_child)
        ans.append(currList)

    flat_list = [item for sublist in ans for item in sublist]
    return flat_list
 
cltz_root = gen_n_levels_deep(9)
 
# левый - через степени двойки
# средний - через прокидывание новых нод от соответствующей двойки
# правый - деление порядковых на три 

stuff = cltz_odd_tree_to_graph(cltz_root)
nodes_n_edges = ''.join(stuff)
cltz_graph_gv = """
digraph G{
    splines=curved
edge [dir="both", arrowtail="dot", arrowhead="normal", arrowsize=0.75,fontsize=9]
node [shape="doublecircle", color="lightblue2", style="filled",fontsize=12,fontnames="bold"]

%s
}
""" % nodes_n_edges
cltz_graph = Source(cltz_graph_gv,
    engine="neato",
    filename="cltz_odds_graph.gv", format="png")
cltz_graph.unflatten(stagger=3).view()

Теперь, зная всё это мы можем построить функцию обратного хода от произвольного нечётного числа к единице сугубо по нечётным числам.

Для этого достаточно прописать обратные функции к функциям переходов использованных для построения графа.

$\begin{align} f_l(n) & \rightarrow & \frac {n + 1} 4 \\ f_{с_0}(n) & \rightarrow & \frac {3(n + 1)} 8 \\ f_{с_1}(n) & \rightarrow & \frac {3n + 1} 4 \\ f_r(n) & \rightarrow & \frac {3n} 2 \\ & ... \end{align}$

Тут можно обойтись даже без использования типизации вершин, т.к целое число за раз почти всегда получается лишь на одной из четырёх из них (напомню, для случая 2 - перехода через первую "генерирующую вершину" - используется две разные функции).

Двойной ответ может происходить при одновременном срабатывании и $f_{c_{0,1}}(n)$ , в таком случае приоритет имеют переходы $f_{c_{0,1}}(n)$ .

from decimal import Decimal


def translate_from_cltz_ordinal(n):
    return Decimal(n) * 2 - 1 
def translate_to_cltz_ordinal(n):
    return int( (Decimal(n) + 1) / 2 )

def f_l(n):
    return (n+1)/4
def f_c0(n):
    return (n+1)*3/8
def f_c1(n):
    return (n*3+1)/4
def f_r(n):
    return n * 3 / 2


def calc(n):
    return [f_l(n), f_c0(n), f_c1(n), f_r(n)]



def choose_num(lst):
    ans = -1

    # [27.0, 40.5, 80.5, 123.0,160.5] 
    ans_lst = [ str(i)[-2:] in ['.0'] for i in lst ]
    # [0, 3]
    ans_ind = [i for i, val in enumerate(ans_lst) if val] 

    return lst[ans_ind[-1]]

  
def backward_run_odds(n):

    m = n
    ret = [m]
    while m != 1:
        now_ans = calc(m)
        m = choose_num(now_ans)
        ret.append(m)

    return ret


  
num = translate_to_cltz_ordinal(
    12345
)

l = backward_run_odds(num)
print(l)
print([ int(translate_from_cltz_ordinal(i)) for i in l ])

При каноничном вызове от числа мы получаем такие результаты:

[6173, 4630.0, 6945.0, 5209.0, 3907.0, 
 977.0, 733.0, 550.0, 825.0, 619.0, 155.0, 
 39.0, 15.0, 6.0, 9.0, 7.0, 3.0, 1.0]

[12345, 9259, 13889, 10417, 7813, 1953, 1465, 1099, 
 1649, 1237, 309, 77, 29, 11, 17, 13, 5, 1]

Сравнивая с каноничным случаем оригинальной последовательности мы явно видим здесь лишние числа. Это возникает из-за особенностей графа по которому строится алгоритм поиска.

Модификация возможна, но для этого надо обратить внимание на структуру графа нечётных чисел в сравнении с исходным графом последовательности Коллатца. Переход по "чёрным" рёбрам в оригинальном графе приводит в вершины вида , в текущем же случае мы используем вместо них промежуточные "боковые" остановки.

Собственно, всё что нам теперь нужно - это вести учёт "цветов" рёбер по которым выстраивается движение к единице, после чего выбросить промежуточные "чёрные" переходы.

...

def choose_num_with_edge_types(lst):
    ans = -1

    # [27.0, 40.5, 80.5, 123.0,160.5] 
    ans_lst = [ str(i)[-2:] in ['.0'] for i in lst ]
    # [0, 3]
    ans_ind = [i for i, val in enumerate(ans_lst) if val] 

    ans = ans_ind[-1]
    if ans == 0:
        ret = ('left-black', lst[ans])
    elif ans == 1 or ans == 2:
        ret = ('center-red', lst[ans])
    elif ans == 3:
        ret = ('right-blue', lst[ans])

    return ret
 

def backward_run_odds_with_edge_types(n):

    m = ('first', n)
    ret = [m]
    while m[1] != 1:
        now_ans = calc(m[1]) 
        m = choose_num_with_edge_types(now_ans)
        ret.append(m)

    return ret


def make_repaired_odds_list(l):
    l2 = [(i[0], i[1], translate_from_cltz_ordinal(i[1])) for i in l] 
    l3 = [i for i in l2 if (i[0] != 'left-black') ]
    l3.append(l2[-1])
    return l3
  
...

l = backward_run_odds_with_edge_types(num) 
l2 = make_repaired_odds_list(l)
print([int(i[2]) for i in l2])

В данном случае вывод будет уже идентичен каноничному:

[12345, 9259, 13889, 10417, 7813, 1465, 1099, 
 1649, 1237, 29, 11, 17, 13, 5, 1]

Исходя из вышеизложенного, можно утверждать, что сей алгоритм корректным образом выводит список заходов последовательности Коллатца в нечётные числа без промежуточного использования чётных.

Пожалуй, здесь уже можно остановиться и далее рихтовать лишь косметические моменты.

Источник: https://habr.com/ru/post/683788/

Вернуться к списку

Интересные статьи

Генерация строго-типизированных коллекций в PHP

Отсутствие коллекций — боль в заднице PHP. На данный момент нет удобного способа обеспечить безопасность типов для наборов объектов. Добавление на уровне языка поддержки дженериков или типиз...

Собираем квантовый генератор случайных чисел

Цель этого проекта – создать настоящий квантовый генератор случайных чисел, то есть устройство, производящее на основе квантовых эффектов случайные числа. За реализацию случайности в не...

Обзор сервисов интеграции WhatsApp (Wazzup, i2crm, Chat2Desk, Pact.im, OLChat) с CRM Битрикс24

Один из ключевых сценариев работы в CRM это общение с клиентом в удобном для него канале. По почте, по телефону, по SMS или в мессенджере. Особенно выделяется WhatsApp — интеграцию с ...

Ошибки при организации продаж в разные регионы через интернет-магазин 1С-Битрикс

В 2019 году люди знакомятся с брендом, выбирают и, что самое главное, ПОКУПАЮТ через интернет. Сегодня практически у любого бизнеса есть свой сайт — от личных блогов, зарабатывающих на рекламе, до инт...

Парсим курсы валют на php и кешируем их в 1с-Битрикс

Довольно часто владельцы сайтов просят поставить на свои проекты индикаторы курсов валют и их динамику. Можно воспользоваться готовыми информерами, но они не всегда позволяют должным образом настроить...