Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
В цифровой обработке сигналов оконные функции широко используются для ограничения сигнала во времени и их названия хорошо известны всем, кто так или иначе сталкивался с дискретным преобразованием Фурье: Ханна, Хэмминга, Блэкмана, Харриса и прочие. Но являются ли они достаточными, можно ли придумать что-то новое и есть ли в этом смысл?
В этой статье мы рассмотрим вывод оконной функции с новыми свойствами, используя Wolfram Mathematica. Предполагается также, что читатель имеет общие представления о цифровой обработке сигналов в контексте обсуждаемого вопроса и как минимум знаком со статьёй из википедии.
Исторически первые оконные функции появлялись в процессе попыток улучшить их спектральные свойства снижением амплитуды боковых лепестков — поскольку при умножении сигнала на оконную функции происходит свёртка их спектров, что вносит некоторые ограничения для анализа. В то время, 50-ые года 20 века, вычислительные мощности не позволяли легко и непринужденно манипулировать символьными вычислениями, и подбор оптимальных параметров представлял достаточную сложность. Это одна из причин, по которой функции названы разными именами — они, а точнее, их спектральные свойства, изучались разными исследователями в течении достаточно длительного времени. Побочным эффектом от этого стало то, что сложившийся набор именованных оконных функций воспринимается как некоторый «стандартный набор», за пределами которого ничего найти уже не возможно; при этом названия этих окон не несут никакой информации о свойствах и предполагают их отдельное изучение и зазубривание.
Все оконные функции получаются произведением некоторой функции на прямоугольную, что гарантированно обеспечивает её ограничение во времени. Поэтому в первую очередь их можно классифицировать по функциям, которые в них используются:
Также их можно поделить по свойствам на краях:
Отдельного упоминания стоят ещё две оконные функции:
Обе они имеют разрывы на краях как значений, так и производных, а вычисления их сопряжены с некоторыми сложностями — функция Кайзера считается через специальную функцию (Бесселя), а Дольфа-Чебышева определяется в частотной области и считается через обратное дискретное преобразование Фурье. Особую сложность также представляет нахождение их аналитических первообразных.
Посмотрим на определения функций Блэкмана и Наттела:
↓
↓
Они представляют из себя суммы из 3-х и 4-х косинусоид с чётными частотами (начиная с нуля) и некоторыми коэффициентами. Откуда взялись эти коэффициенты? Вряд ли они были подобраны вручную, по крайней мере, каждый по отдельности — ведь существуют граничные условия, которым окна должны соответствовать вне зависимости от их спектральных свойств — как минимум, равенство единице в центре.
Попробуем «изобрести» функцию Блэкмана самостоятельно. Для этого определим функцию с пока ещё неизвестными коэффициентами
и составим систему уравнений, определяющих граничные условия — равенства единице в центре, нулю на краях, и равенства нулю производных на краях:
↓

Решение нашлось, но не одно, а множество — в зависимости от коэффициента a, о чём Wolfram нас учтиво предупредил. Теперь из найденного решения зададим новую функцию, зависящую от неизвестного коэффициента:
↓

Легко видеть, что при a=0.42 получим функцию Блэкмана. Но почему именно 0.42?
Для ответа на этот вопрос нам нужно построить её спектр. Аналитическое преобразование Фурье — не самая простая задача, но Wolfram справляется и с ней, избавляя нас от рутинной работы.
↓


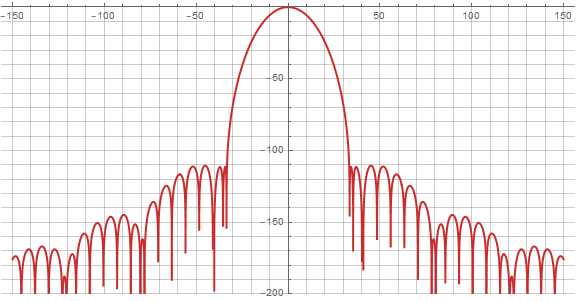
В таком виде график функции пока ещё мало информативен, поскольку спектр удобнее анализировать в логарифмическом масштабе. Добавив соответствующее преобразование в децибелы , получим тот самый привычный график спектра оконных функций:

В процессе изменения параметра мы будем наблюдать нечто подобное:

В зависимости от параметра a меняется уровень боковых лепестков, и при a=0.42 он боле-менее минимальный и равномерный. При а=0.409 мы можем получить результат чуточку лучше, если под «лучше» понимать минимально возможный уровень боковых лепестков.
Очевидно подобная микрооптимизация вовсе не стоила затраченных усилий. Можно ли качественно улучшить свойства этого окна, не изменяя исходных данных?
Ранее мы рассматривали вывод оконных функций, суммирующихся в единицу, что позволяет восстанавливать исходный сигнал. Попробуем применить эту технику для нашего окна и посмотрим, как она отразится на спектре.
Определим вспомогательную функцию для построения перекрывающихся окон с учётом границ изменения аргумента в диапазоне от -1/2 до 1/2:

Находим первообразную, смещаем её к центру координат и масштабируем к единице:

↓

выводим её на график:

Как видим, Wolfram здесь тоже справился самостоятельно и нам не пришлось вручную задавать кусочно-непрерывное определение первообразной. Теперь вид нашего окна зависит не только от переменной a, но от степени перекрытия — и по мере его увеличения будет стремится к форме производной:

И последний штрих — найти аналитическую функцию для спектра, чтобы определить оптимальное значение параметра a.
Здесь, если мы попробуем вычислить преобразование непосредственно, как в прошлый раз — то вгоним Wolfram в глубокую задумчивость. Есть несколько способов ускорить этот процесс:
— использовать дискретное преобразование вместо аналитического — наиболее простое. Но настоящий математик не будет применять численные методы там, где можно найти чисто аналитическое решение — и мы (пока) не будем; к тому же у него есть очевидные ограничения (по разрешению и ограничению спектра);
— передавать в качестве параметра перекрытия конкретные значения и, глядя на результаты, попытаться увидеть закономерность и обобщить их. Вполне работающий вариант, но требующих дополнительных умственных и творческих усилий. Оставим его на крайний случай.
— производить вычисления непосредственно в частотном домене. Это возможно благодаря следующим свойствам преобразования Фурье:
1) оно линейно, т.е. сумма образов равно образу суммы;
2) интегрирование во временном домене равносильно делению на i w в частотном.
3) смещение во времени равносильно модуляцией комплексной синусоидой.
(подробнее в википедии или тут).
Таким образом, имея спектр hw произвольной оконной функции, мы можем получить из него спектр hwo суммирующейся в единицу функции с перекрытием t:
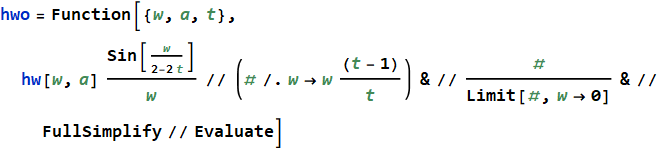
↓
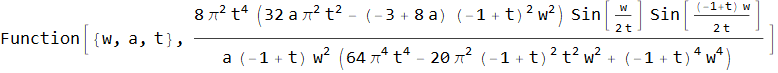
Теперь можно посмотреть, как меняется спектр в динамике:

Здесь изменение параметра перекрытия уже будет влиять на спектр окна несколько по-другому:

Немного поигравшись с параметрами легко заметить, что «больше — не значит лучше», и оптимальная степень перекрытия для той функции находится в районе четырёх. Конкретно, для t=4 и a=0.404 мы получаем уровень боковых лепестков, не превышающий -80 дБ. Это очень даже неплохой результат — особенно учитывая, что функция приподнятого косинуса, традиционно используемая для суммируемых в единицу окон, даёт уровень лепестков примерно в -30 дБ. Ну а выписанная явном образом наша новая оконная функция будет выглядеть так:
Что ещё можно сделать, чтобы ещё более снизить уровень боковых лепестков? Можно взять косинусы не с чётными, а с нечётными частотами (здесь для компактности решение системы уравнений внедрено непосредственно в определение функции):
и после интегрирования с параметрами a=0.6628 и уровнем перекрытия 4.5 получить подавление в -90 дБ:

В явном виде:
Можно добавить ещё один косинус и увеличить количество нулевых производных:
и после интегрирования с параметрами a=0.5862 и уровнем перекрытия 6.4 получить подавление в -110 дБ:

В явном виде:
Ещё более значительного снижения уровня боковых лепестков можно добиться, возведя Фурье-образ в квадрат и тем самым снизив уровень боковых лепестков сразу в 2 раза. Это позволяет избавится от увеличения количества параметров для их ручного подбора, но добавляет сложности в вычислении свёртки во временном домене.

и здесь уже можно добиться подавления свыше 160 дБ:

Формулу в явном виде приводить не будем из-за её внушительного размера.
Для обеспечения нужного количества нулей на границах нашей функции мы использовали поиск через решение системы уравнений с последующим интегрированием. Это не очень удобно — ведь нужно каждый раз менять количество уравнений. Может, есть более просто и красивое решение? Есть! И поможет нам в этом гипергеометрическая функция.
Наше решение будет выглядеть следующим образом:
где
Она состоит из суммы двух частей: первообразная от функции , нормированной по амплитуде к точке (1,1) и функцией со свободными параметрами, помноженных на ту же для того, чтобы сохранить необходимое количество нулевых производных:

От того, какую именно функцию мы выберем для корректировки формы, будут зависеть точность настройки и их влияние на распределение боковых лепестков — тут возможны варианты, требующие отдельных исследований. В данном случае функция даёт вполне приемлемый вариант — и за счёт двух параметров позволяет делать более точную настройку.
Сама же формула интересна (и удобна) тем, что при чётных n упрощается до полинома, а при нечётных — до суммы полинома с арксинусом и квадратным корнем — что делает итоговую формулу более компактной и более простой для вычислений.
Подбирать параметры здесь уже проще (и быстрее) через дискретное преобразование Фурье. Нам также потребуется дополнительное определение overlap-функции для работы с тремя параметрами:




В качестве примера, после подстановки параметров с картинки наша функция упростится до
Если задача суммирования окон в единицу не стоит, то наиболее оптимальным окном является окно Кайзера, позволяющее плавно регулировать ширину основного лепестка. Однако у него есть недостаток — поскольку оно выражается через функцию Бесселя, считать его за пределами математических пакетов несколько затруднительно. Можно, конечно, отдельно реализовать функцию Бесселя — а можно и поискать аппроксимацию через элементарные функции. И неожиданно оказалось, что используя для этого функцию спектра окна Кайзера (ограниченного во времени) можно получить результат даже чуточку лучше —
Расплатой за такое хитрое решение оказалось невозможность выразить её спектр чисто аналитически — но это не так и важно, поскольку на практике мы в любом случае оперируем и анализируем данные в дискретном виде используя дискретное же преобразование Фурье. Ниже на графике можно сравнить их спектры, где красным — оригинальное окно Кайзера, зелёным — его аппроксимация:

При той же ширине основного лепестка уровень боковых лепестков получается несколько ниже. А для удобства использования можно составить таблицу с ориентировочными значениями параметра k для получения необходимого уровня подавления боковых лепестков:
Отдельной интересной задачей остаётся нахождение аппроксимации первообразной инверсного окна Кайзера. Пока что удалось только выразить его через степенной ряд, который довольно медленно сходится:
Возможно, специалисты в математике смогут подсказать более лучшее решение в комментариях.
Несмотря на то, что цифровая обработка сигналов является вполне себе сформировавшейся дисциплиной, в ней есть ещё куда развиваться и находить что-то новое — как минимум в существующей специальной и научной литературе вопросы построения суммирующихся в единицу оконных функций не рассматривается; а возможности современных систем компьютерной алгебры позволяют переосмыслить накопленные знания на качественно новом уровне.
Исходный документ Wolfram Mathematica со всеми вычислениями доступен на GitHub.
В этой статье мы рассмотрим вывод оконной функции с новыми свойствами, используя Wolfram Mathematica. Предполагается также, что читатель имеет общие представления о цифровой обработке сигналов в контексте обсуждаемого вопроса и как минимум знаком со статьёй из википедии.

Введение
Исторически первые оконные функции появлялись в процессе попыток улучшить их спектральные свойства снижением амплитуды боковых лепестков — поскольку при умножении сигнала на оконную функции происходит свёртка их спектров, что вносит некоторые ограничения для анализа. В то время, 50-ые года 20 века, вычислительные мощности не позволяли легко и непринужденно манипулировать символьными вычислениями, и подбор оптимальных параметров представлял достаточную сложность. Это одна из причин, по которой функции названы разными именами — они, а точнее, их спектральные свойства, изучались разными исследователями в течении достаточно длительного времени. Побочным эффектом от этого стало то, что сложившийся набор именованных оконных функций воспринимается как некоторый «стандартный набор», за пределами которого ничего найти уже не возможно; при этом названия этих окон не несут никакой информации о свойствах и предполагают их отдельное изучение и зазубривание.
Классификация
Все оконные функции получаются произведением некоторой функции на прямоугольную, что гарантированно обеспечивает её ограничение во времени. Поэтому в первую очередь их можно классифицировать по функциям, которые в них используются:
- сумма косинусов. Наиболее обширный класс по причине того, что их спектр легко вычислим и представляет из себя сумму взвешенных sinc-функций. Сюда входят Hann, Hamming, Blackman, Harris ...
- кусочно-непрерывные полиномиальные. Получаются в результате свёртки простых функций — например, прямоугольной и треугольной. Их спектры при этом перемножаются и их нахождение так же не представляет особых сложностей. Сюда входят Dirichlet, Triangular, Parzen, Welch...
- все прочие — с использованием экспонент, гауссиан, sinc и других, выбор конкретных функций в которых носит скорее идейный характер, нежели конкретно спектральные свойства.
Также их можно поделить по свойствам на краях:
- отсутствие разрывов на краях — равенство нулю значений. Разрывы имеют Dirichlet, Hamming, Blackman-Harris. Не имеют — Triangular, Hann, Nuttal
- отсутствие разрывов 1-ой и прочих производных
Отдельного упоминания стоят ещё две оконные функции:
- Кайзера, позволящей задавать ширину главного лепестка;
- Дольфа-Чебышева, все боковые лепестки которой равны заданной амплитуде.
Обе они имеют разрывы на краях как значений, так и производных, а вычисления их сопряжены с некоторыми сложностями — функция Кайзера считается через специальную функцию (Бесселя), а Дольфа-Чебышева определяется в частотной области и считается через обратное дискретное преобразование Фурье. Особую сложность также представляет нахождение их аналитических первообразных.
Исследовать оконные функции на разрывы можно следующим простым кодом:
↓

wins = {DirichletWindow, HammingWindow, BlackmanWindow,
BartlettHannWindow, BartlettWindow, BlackmanHarrisWindow,
BlackmanNuttallWindow, BohmanWindow, ExactBlackmanWindow,
FlatTopWindow, KaiserBesselWindow, LanczosWindow, NuttallWindow};
Table[{f,
Table[Limit[D[f[x], {x, k}], x -> 1/2,
Direction -> "FromBelow"], {k, 0, 4}]}, {f, wins}]</code>
↓
<img src="https://habrastorage.org/webt/rm/wq/8f/rmwq8fjkjxjcox-czh8zevkbd0m.png" />
<code>Plot[Evaluate[Through[wins[x]]], {x, -1, 1}, PlotRange -> {-0.25, 1},
GridLines -> {{-0.5, -0.25, 0.25, 0.5, 1}}, AspectRatio -> 5/8,
PlotLegends -> "Expressions"]↓

Реверс инжиниринг
Посмотрим на определения функций Блэкмана и Наттела:
BlackmanWindow[x] // FunctionExpand↓
NuttallWindow[x] // FunctionExpand↓
Они представляют из себя суммы из 3-х и 4-х косинусоид с чётными частотами (начиная с нуля) и некоторыми коэффициентами. Откуда взялись эти коэффициенты? Вряд ли они были подобраны вручную, по крайней мере, каждый по отдельности — ведь существуют граничные условия, которым окна должны соответствовать вне зависимости от их спектральных свойств — как минимум, равенство единице в центре.
Попробуем «изобрести» функцию Блэкмана самостоятельно. Для этого определим функцию с пока ещё неизвестными коэффициентами
f = Function[x, a + b Cos[2 Pi x] + c Cos[4 Pi x]];и составим систему уравнений, определяющих граничные условия — равенства единице в центре, нулю на краях, и равенства нулю производных на краях:
ss = Solve[{
f[0] == 1,
f[1/2] == 0,
f'[1/2] == 0
}, {a, b, c}]↓

Решение нашлось, но не одно, а множество — в зависимости от коэффициента a, о чём Wolfram нас учтиво предупредил. Теперь из найденного решения зададим новую функцию, зависящую от неизвестного коэффициента:
hx = Function[{x, a},
Piecewise[{{f[x] /. ss[[1]], -1/2 < x < 1/2}}, 0] // Evaluate]↓

Легко видеть, что при a=0.42 получим функцию Блэкмана. Но почему именно 0.42?
Для ответа на этот вопрос нам нужно построить её спектр. Аналитическое преобразование Фурье — не самая простая задача, но Wolfram справляется и с ней, избавляя нас от рутинной работы.
hw = Function[{w, a},
FourierTransform[hx[x, a], x, w] // #/Limit[#, w -> 0] & //
Simplify // Evaluate]↓

примечание
В отличие от многих других операций, в команде FourierTransform нужно указывать не одну переменную, а две — в том числе и для того, чтобы не путаться, в какой области находится определение функции — временном или частотном. Традиционно для частотной области используется переменная w. Здесь мы заодно нормировали функцию к единице в центре координат — но не прямой подстановкой нуля в w, поскольку это вызывает деление на ноль, а через нахождение предела.

В таком виде график функции пока ещё мало информативен, поскольку спектр удобнее анализировать в логарифмическом масштабе. Добавив соответствующее преобразование в децибелы , получим тот самый привычный график спектра оконных функций:
код
Manipulate[
Plot[{
hw[w, a],
hw[w, 0.42]
} // Abs // 20 Log[10, #] & // Evaluate
, {w, -111, 111}, PlotRange -> {-120, 0}, GridLines -> Automatic,
PlotStyle -> {Default, Thin}, PlotPoints -> 50]
, {{a, 0.409}, 0.3, 0.5}]
↓
В процессе изменения параметра мы будем наблюдать нечто подобное:

В зависимости от параметра a меняется уровень боковых лепестков, и при a=0.42 он боле-менее минимальный и равномерный. При а=0.409 мы можем получить результат чуточку лучше, если под «лучше» понимать минимально возможный уровень боковых лепестков.
примечание
Здесь можно вспомнить, что во времена становления теории ЦОС никаких Вольфрамов с интерактивными графиками не было и все эти вычисления и поиск оптимальных параметров производился вручную, ручкой на бумаге.
Развитие
Очевидно подобная микрооптимизация вовсе не стоила затраченных усилий. Можно ли качественно улучшить свойства этого окна, не изменяя исходных данных?
Ранее мы рассматривали вывод оконных функций, суммирующихся в единицу, что позволяет восстанавливать исходный сигнал. Попробуем применить эту технику для нашего окна и посмотрим, как она отразится на спектре.
Определим вспомогательную функцию для построения перекрывающихся окон с учётом границ изменения аргумента в диапазоне от -1/2 до 1/2:

Находим первообразную, смещаем её к центру координат и масштабируем к единице:

↓

выводим её на график:

Как видим, Wolfram здесь тоже справился самостоятельно и нам не пришлось вручную задавать кусочно-непрерывное определение первообразной. Теперь вид нашего окна зависит не только от переменной a, но от степени перекрытия — и по мере его увеличения будет стремится к форме производной:
код
↓
Manipulate[
Plot[
OverlapShape[hsx, x, a, t]
, {x, -1, 1}, PlotRange -> All, GridLines -> Automatic]
, {{a, 0.404}, 0.4, 0.5}, {{t, 4}, 3, 11}]↓

И последний штрих — найти аналитическую функцию для спектра, чтобы определить оптимальное значение параметра a.
Здесь, если мы попробуем вычислить преобразование непосредственно, как в прошлый раз — то вгоним Wolfram в глубокую задумчивость. Есть несколько способов ускорить этот процесс:
— использовать дискретное преобразование вместо аналитического — наиболее простое. Но настоящий математик не будет применять численные методы там, где можно найти чисто аналитическое решение — и мы (пока) не будем; к тому же у него есть очевидные ограничения (по разрешению и ограничению спектра);
— передавать в качестве параметра перекрытия конкретные значения и, глядя на результаты, попытаться увидеть закономерность и обобщить их. Вполне работающий вариант, но требующих дополнительных умственных и творческих усилий. Оставим его на крайний случай.
— производить вычисления непосредственно в частотном домене. Это возможно благодаря следующим свойствам преобразования Фурье:
1) оно линейно, т.е. сумма образов равно образу суммы;
2) интегрирование во временном домене равносильно делению на i w в частотном.
3) смещение во времени равносильно модуляцией комплексной синусоидой.
(подробнее в википедии или тут).
Таким образом, имея спектр hw произвольной оконной функции, мы можем получить из него спектр hwo суммирующейся в единицу функции с перекрытием t:
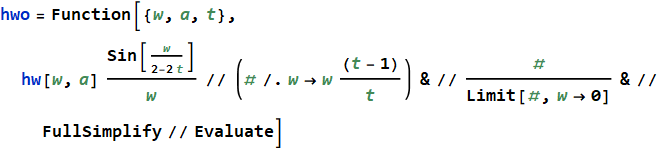
↓
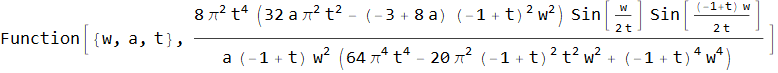
Теперь можно посмотреть, как меняется спектр в динамике:

Здесь изменение параметра перекрытия уже будет влиять на спектр окна несколько по-другому:

Немного поигравшись с параметрами легко заметить, что «больше — не значит лучше», и оптимальная степень перекрытия для той функции находится в районе четырёх. Конкретно, для t=4 и a=0.404 мы получаем уровень боковых лепестков, не превышающий -80 дБ. Это очень даже неплохой результат — особенно учитывая, что функция приподнятого косинуса, традиционно используемая для суммируемых в единицу окон, даёт уровень лепестков примерно в -30 дБ. Ну а выписанная явном образом наша новая оконная функция будет выглядеть так:
код
↓
OverlapShape[hsx, x, 404/1000, 4] // PiecewiseExpand // FullSimplify↓
Дальнейшее развитие
Что ещё можно сделать, чтобы ещё более снизить уровень боковых лепестков? Можно взять косинусы не с чётными, а с нечётными частотами (здесь для компактности решение системы уравнений внедрено непосредственно в определение функции):
код
↓
hx1 = Function[{x, a},
a Cos[1 Pi #] + b Cos[3 Pi #] + c Cos[5 Pi #] & // #[x] /. Solve[{
#[0] == 1,
#[1/2] == 0,
#'[1/2] == 0,
#''[1/2] == 0
}, {a, b, c}][[1]] & // # UnitBox[x] & // Evaluate]↓
и после интегрирования с параметрами a=0.6628 и уровнем перекрытия 4.5 получить подавление в -90 дБ:

В явном виде:
Можно добавить ещё один косинус и увеличить количество нулевых производных:
код
↓
hx2 = Function[{x, a},
a Cos[1 Pi #] + b Cos[3 Pi #] + c Cos[5 Pi #] +
d Cos[7 Pi #] & // #[x] /. Solve[{
#[0] == 1,
#[1/2] == 0,
#'[1/2] == 0,
#''[1/2] == 0,
#'''[1/2] == 0,
#''''[1/2] == 0
}, {b, c, d}][[1]] & // # UnitBox[x] & // Evaluate]↓
и после интегрирования с параметрами a=0.5862 и уровнем перекрытия 6.4 получить подавление в -110 дБ:

В явном виде:
Ещё более значительного снижения уровня боковых лепестков можно добиться, возведя Фурье-образ в квадрат и тем самым снизив уровень боковых лепестков сразу в 2 раза. Это позволяет избавится от увеличения количества параметров для их ручного подбора, но добавляет сложности в вычислении свёртки во временном домене.
код
↓
hx3 = Function[{x, a},
Convolve[hx1[x, a], hx1[x, a], x, y] /. y -> 2 x
// FullSimplify // Evaluate]↓

и здесь уже можно добиться подавления свыше 160 дБ:

Формулу в явном виде приводить не будем из-за её внушительного размера.
Гипергеометрические оконные функции
Для обеспечения нужного количества нулей на границах нашей функции мы использовали поиск через решение системы уравнений с последующим интегрированием. Это не очень удобно — ведь нужно каждый раз менять количество уравнений. Может, есть более просто и красивое решение? Есть! И поможет нам в этом гипергеометрическая функция.
вкратце о гипергеометрических функциях
Из курса матанализа нам известно, что практически любую функцию можно разложить в степенной ряд. Гипергеометрические функции решают прямо противоположную задачу — определяют функцию через её степенной ряд, задавая конечный набор некоторых коэффициентов и правило вычисления произвольного члена ряда в зависимости от них. Это позволяет оперировать большим количеством функций без задания им явных имён — в том числе и уже известными.
Наше решение будет выглядеть следующим образом:
где
Она состоит из суммы двух частей: первообразная от функции , нормированной по амплитуде к точке (1,1) и функцией со свободными параметрами, помноженных на ту же для того, чтобы сохранить необходимое количество нулевых производных:

От того, какую именно функцию мы выберем для корректировки формы, будут зависеть точность настройки и их влияние на распределение боковых лепестков — тут возможны варианты, требующие отдельных исследований. В данном случае функция даёт вполне приемлемый вариант — и за счёт двух параметров позволяет делать более точную настройку.
Сама же формула интересна (и удобна) тем, что при чётных n упрощается до полинома, а при нечётных — до суммы полинома с арксинусом и квадратным корнем — что делает итоговую формулу более компактной и более простой для вычислений.
Подбирать параметры здесь уже проще (и быстрее) через дискретное преобразование Фурье. Нам также потребуется дополнительное определение overlap-функции для работы с тремя параметрами:




В качестве примера, после подстановки параметров с картинки наша функция упростится до
код

↓

↓
Инверсное окно Кайзера
Если задача суммирования окон в единицу не стоит, то наиболее оптимальным окном является окно Кайзера, позволяющее плавно регулировать ширину основного лепестка. Однако у него есть недостаток — поскольку оно выражается через функцию Бесселя, считать его за пределами математических пакетов несколько затруднительно. Можно, конечно, отдельно реализовать функцию Бесселя — а можно и поискать аппроксимацию через элементарные функции. И неожиданно оказалось, что используя для этого функцию спектра окна Кайзера (ограниченного во времени) можно получить результат даже чуточку лучше —
примечание
В точках функция имеет особую точку, которая находится через предел и равна .
Расплатой за такое хитрое решение оказалось невозможность выразить её спектр чисто аналитически — но это не так и важно, поскольку на практике мы в любом случае оперируем и анализируем данные в дискретном виде используя дискретное же преобразование Фурье. Ниже на графике можно сравнить их спектры, где красным — оригинальное окно Кайзера, зелёным — его аппроксимация:
код

↓

↓

При той же ширине основного лепестка уровень боковых лепестков получается несколько ниже. А для удобства использования можно составить таблицу с ориентировочными значениями параметра k для получения необходимого уровня подавления боковых лепестков:
Отдельной интересной задачей остаётся нахождение аппроксимации первообразной инверсного окна Кайзера. Пока что удалось только выразить его через степенной ряд, который довольно медленно сходится:
Возможно, специалисты в математике смогут подсказать более лучшее решение в комментариях.
Заключение
Несмотря на то, что цифровая обработка сигналов является вполне себе сформировавшейся дисциплиной, в ней есть ещё куда развиваться и находить что-то новое — как минимум в существующей специальной и научной литературе вопросы построения суммирующихся в единицу оконных функций не рассматривается; а возможности современных систем компьютерной алгебры позволяют переосмыслить накопленные знания на качественно новом уровне.
Исходный документ Wolfram Mathematica со всеми вычислениями доступен на GitHub.


![DeepFake своими руками [часть 1] DeepFake своими руками [часть 1]](/upload/resize_cache/iblock/e6e/105_70_0/e6ec5c2bfad5a2a5de50349fa0a6908c.jpeg)