Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
Habritants! В этой статье описано получение метрики общего вида, включающей метрики Фридмана и Шварцшильда как частные случаи.
Для понимания материала необходимы знания алгебры: понятие о производных в большей степени; тензорная — в меньшей.
Представим, что у пространства есть четвёртое измерение. Как если бы движение в нём забирало у объекта некоторое количество движения или наоборот. Словно гравитация это чисто геометрический эффект создания субпространственной воронки вокруг любого объекта, обладающего энергией.
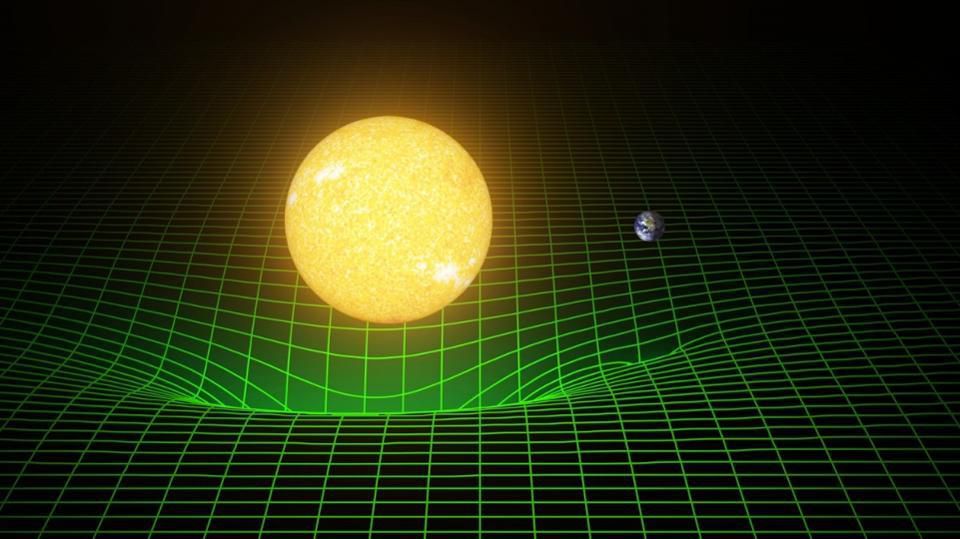
Вы наверняка натыкались на подобную визуализацию гравитации, если интересуетесь вопросом:
Для того, чтобы оценить глубину такой воронки и механизм взаимодействия объектов, сформулируем выражение интервала сигнатуры (1-4).
Представим 4-ёх мерное пространство , и зададим в нём сферические координаты :
Для этого запишем переходную матрицу:
Посчитаем переходные коэффициенты:
И представим соответствующий интервал:
Красным — темпоральная составляющая, представленная аналогично метрике FLRW.
Зелёным — пространственная составляющая, представленная аналогично метрике FLRW, и представляющая собой поверхность 3-сферы.
Маджента получилась подвисшим между временем и пространством звеном — дифференциалом изменения мультипликатора пространственной части.
Продолжая развитие идей, изложенных в предыдущей статье, положим изменение четвёртого измерения мерой связанной с относительным количеством энергии объектов, следовательно, дополним метрику составляющей в силу рассмотрения энергетически замкнутой системы, что будет предполагаться истинным и для Вселенной в целом (решение Фридмана), и для сферически симметричного массивного тела (решение Шварцшильда). Читатель не согласный с такой трактовкой, может просто считать это математическим трюком:
Маджента в темпоральной части понятна:
Зелёную переформируем, чтобы показать, что пространство является псевдоевклидовым:
Производные углов по углу равны:
Поэтому с учётом базисных векторов:
что представляет локальное псевдоевклидово 3-пространство с линейными по базисными векторами:
с масштабным фактором , и с мгновенной длиной , в нашем случае совокупно редуцированной на величину :
Без оранжевой составляющей получилась пространственная часть интервала стандартной космологической модели для «плоского» пространства с возможной деградацией пространственного масштабного фактора по времени, как в FLRW.
Гиперповерхность 3-сферы является внутри себя линейной по угловым координатам, или, иначе говоря, пространственная часть интервала получилась «плоской» для неизменного . «Упаковать» лишний будет практичнее снова в сферических, только уже обычных для трёхмерной сферы . Чтобы различать координаты для 3-сферической и 2-сферической систем, последние обозначим :
где порядок отношения величин , а по теореме тангенсов:
Тогда полный интервал будет:
Получился комбинированный интервал словно «слепленный» из вида интервала метрики FLRW и метрики Шварцшильда, каждый из которых представляет частный случай физических взаимодействий. Теперь посмотрим как из получаются соответствующие решения.
Чисто математически интервал вида превращается в метрику FLRW стандартной космологической модели простым исключением энергетической составляющей :
Что, как показано выше, можно также переписать так:
Решение уравнений ОТО для такого интервала даёт зависимость .
Однако, эмпирические данные ККС для объектов показывают консолидированное отклонение от этой зависимости.
Возможно, решение для интервала вида даст более точную зависимость, но я пока его не нашёл.
Сравним полученный интервал с метрикой Шварцшильда:
Если представить систему взаимодействующих объектов в низкоэнергетическом масштабе , то можно принять равным единице без потери математической связности, пространство при этом станет псевдоевклидовым, а интервал можно переписать следующим образом:
Математически это ровно то же самое, как если бы мы выполнили фокус для пустого 3-пространства в сферических координатах .
То есть для плоского вакуумного случая интервал будет иметь решение аналогичное решению метрики Шварцшильда, при условии эквивалентности подцвеченных красным и оранжевым множителей. Получим систему:
где — по порядку: время, кривизна (энергия), радиус (расстояние) в сферически симметричном гравитационном поле по нулевой общей кривизне пространства.
Путём нехитрых математических преобразований получим весьма лаконичное решение:
которое подтверждает, что:
Первое, на мой взгляд, очень важно, потому что показывает, что энергия, представленная как дополнительная ось, почти изотропна наблюдаемым. Второе — позволяет понять, почему она проявляет себя иначе. И «ненаблюдаема».
Кроме того, хочется отметить, что сама постановка в интервале энергии с отрицательным знаком относительно пространства и положительным относительно времени позволяет сформулировать их взаимоотношения следующим образом: пространство — это энергия-время, оно преодолевается за энергию-время.
Мне кажется, продолжение курса на геометризацию физики показывает себя весьма перспективным направлением. Мнимость энергетической оси в космологии могла бы послужить перекидным мостиком к уравнениям Максвелла.
Для понимания материала необходимы знания алгебры: понятие о производных в большей степени; тензорная — в меньшей.
Представим, что у пространства есть четвёртое измерение. Как если бы движение в нём забирало у объекта некоторое количество движения или наоборот. Словно гравитация это чисто геометрический эффект создания субпространственной воронки вокруг любого объекта, обладающего энергией.
Вы наверняка натыкались на подобную визуализацию гравитации, если интересуетесь вопросом:

Для того, чтобы оценить глубину такой воронки и механизм взаимодействия объектов, сформулируем выражение интервала сигнатуры (1-4).
3-сферические координаты
Представим 4-ёх мерное пространство , и зададим в нём сферические координаты :
Для этого запишем переходную матрицу:
Посчитаем переходные коэффициенты:
И представим соответствующий интервал:
Красным — темпоральная составляющая, представленная аналогично метрике FLRW.
Зелёным — пространственная составляющая, представленная аналогично метрике FLRW, и представляющая собой поверхность 3-сферы.
Маджента получилась подвисшим между временем и пространством звеном — дифференциалом изменения мультипликатора пространственной части.
Общий вид интервала
Продолжая развитие идей, изложенных в предыдущей статье, положим изменение четвёртого измерения мерой связанной с относительным количеством энергии объектов, следовательно, дополним метрику составляющей в силу рассмотрения энергетически замкнутой системы, что будет предполагаться истинным и для Вселенной в целом (решение Фридмана), и для сферически симметричного массивного тела (решение Шварцшильда). Читатель не согласный с такой трактовкой, может просто считать это математическим трюком:
Маджента в темпоральной части понятна:
Зелёную переформируем, чтобы показать, что пространство является псевдоевклидовым:
Производные углов по углу равны:
Поэтому с учётом базисных векторов:
что представляет локальное псевдоевклидово 3-пространство с линейными по базисными векторами:
с масштабным фактором , и с мгновенной длиной , в нашем случае совокупно редуцированной на величину :
Без оранжевой составляющей получилась пространственная часть интервала стандартной космологической модели для «плоского» пространства с возможной деградацией пространственного масштабного фактора по времени, как в FLRW.
Гиперповерхность 3-сферы является внутри себя линейной по угловым координатам, или, иначе говоря, пространственная часть интервала получилась «плоской» для неизменного . «Упаковать» лишний будет практичнее снова в сферических, только уже обычных для трёхмерной сферы . Чтобы различать координаты для 3-сферической и 2-сферической систем, последние обозначим :
где порядок отношения величин , а по теореме тангенсов:
Тогда полный интервал будет:
Получился комбинированный интервал словно «слепленный» из вида интервала метрики FLRW и метрики Шварцшильда, каждый из которых представляет частный случай физических взаимодействий. Теперь посмотрим как из получаются соответствующие решения.
Вид интервала для метрики Фридмана
Чисто математически интервал вида превращается в метрику FLRW стандартной космологической модели простым исключением энергетической составляющей :
Что, как показано выше, можно также переписать так:
Решение уравнений ОТО для такого интервала даёт зависимость .
Однако, эмпирические данные ККС для объектов показывают консолидированное отклонение от этой зависимости.
Возможно, решение для интервала вида даст более точную зависимость, но я пока его не нашёл.
Решение ОТО через метрику Шварцшильда
Сравним полученный интервал с метрикой Шварцшильда:
Если представить систему взаимодействующих объектов в низкоэнергетическом масштабе , то можно принять равным единице без потери математической связности, пространство при этом станет псевдоевклидовым, а интервал можно переписать следующим образом:
Математически это ровно то же самое, как если бы мы выполнили фокус для пустого 3-пространства в сферических координатах .
То есть для плоского вакуумного случая интервал будет иметь решение аналогичное решению метрики Шварцшильда, при условии эквивалентности подцвеченных красным и оранжевым множителей. Получим систему:
где — по порядку: время, кривизна (энергия), радиус (расстояние) в сферически симметричном гравитационном поле по нулевой общей кривизне пространства.
Путём нехитрых математических преобразований получим весьма лаконичное решение:
которое подтверждает, что:
- Четвёртая координата линейна радиальной координате.
- Четвёртая координата является координатой по мнимой оси.
Первое, на мой взгляд, очень важно, потому что показывает, что энергия, представленная как дополнительная ось, почти изотропна наблюдаемым. Второе — позволяет понять, почему она проявляет себя иначе. И «ненаблюдаема».
Кроме того, хочется отметить, что сама постановка в интервале энергии с отрицательным знаком относительно пространства и положительным относительно времени позволяет сформулировать их взаимоотношения следующим образом: пространство — это энергия-время, оно преодолевается за энергию-время.
Резюме
Мне кажется, продолжение курса на геометризацию физики показывает себя весьма перспективным направлением. Мнимость энергетической оси в космологии могла бы послужить перекидным мостиком к уравнениям Максвелла.
Заметки на полях. Забегая вперёд, позволю себе предположить, что одного мнимого измерения для организации механизмов заряда и массы будет мало. Плюс электро-магнитный дуализм как аргумент в пользу не менее двух измерений. И некоторая симметрия в форме: временное измерение + два энергетических = три пространственных.
При переходе к микро масштабам я попробую двигаться в направлении «расщепления» :