Предисловие
Думаю, нужно коротко пояснить, почему вдруг такая, казалось бы, тривиальная тема с подсчетом энергобюджета и почему именно спутники CubeSat? Ну, здесь всё достаточно просто: моя короткая педагогическая практика показала (мне), что тема эта хоть и базисная, но далеко не всеми с первого раза понимаемая, а более того имеющая несколько неочевидных в первом прочтении вопросов. Тем более, что, казалось бы, по таким базовым вещам до сих пор публикуют статьи в IEEE и делают это далеко не студенты. Почему именно CubeSat? Здесь всё ещё проще: формат спутника интересный (сам факт существования микро- и наноспутников, как выяснилось, повергает многих в состояние короткого шока), а потому как нельзя кстати подходящий для учебных целей.

Моделирование будет проведено на языке python 3 по тем же причинам, что я высказывал в своей предыдущей публикации. Рассматривать будем низкоорбитальный случай (LEO — Low Earth Orbit), а посчитаем, собственно, отношение сигнал-шум (SNR — Signal-to-Noise ratio) на входе приемника по нисходящему каналу (DL — Down Link). Воспользуемся несколькими справочниками из открытого доступа и построим графики для наглядности.
Все исходные коды доступны в моём GitHub репозитории, всех интересующихся приглашаю к прочтению! За code review и конструктивную критику буду очень благодарен!
Поехали!
По каким формулам будем подсчитывать?
Во-первых, это конечно же всем (причастным к тематике) известная формула отношения сигнал-шум в логарифмическом масштабе (в децибелах, по-простому), где мы с определенной долей абстракции учитываем все возможное потери и усиления:
где — общая мощность теплового шума (имеет известное отношение к спектральной плотности шума
) в дБм (децибел на миливатт),
— передаваемая мощность в дБм,
и
— коэффициенты усиления антенны на стороне передатчика и приемника соответственно (в дБи — изотропных децибелах),
и
— усиление фидера передатчика и приемника (в дБ),
и
— потери в фидерах (в дБ),
потери на пути распространения электромагнитной волны в дБ,
— дополнительные потери (так сказать, некоторая маржа (margin)) в дБ.
В общем и целом, с первыми семью слагаемыми всё более или менее ясно: данные справочные. Интереснее дела обстоят с последними тремя участниками процесса.
Мощность теплового шума
Как известно, от этого бича радиоэлектронных устройств скрыться некуда, можно только учесть:
где — постоянная Больцмана,
— эквивалентная шумовая температура,
— сумма потерь антенны и шума (фона) неба,
— шумовая температура приемника (
, а
— коэффициент шума, который можно оценить по шумой картине (
— noise figure) приемной антенны), а
— ширина частотной полосы шума. Можно принимать шумовую полосу равной полосе пропускания самого приемника
, однако согласно [1, с.98 ] ширина полосы шума
может быть оценена чуть более точно как
, где
— постоянная от 1,002 до 1,57 (относится к конфигурации приемника).
Дополнительные потери
Здесь можно принять либо какой-то гарантированный запас, почерпнутый, как правило, из тех же справочников, либо углубиться и посчитать всё самостоятельно.
В данном разделе я почти полностью полагаюсь на старый добрый учебник Кантора, а именно на эту его часть [1, p.88-96]. Если у читателей есть более актуальные авторитетные источники — просьба поделиться, я думаю, будет полезно всем.
На что в первую очередь обратим внимание:
- Потери из-за преломления и неточности наведения антенны (Antenna Beam Loss)
Обозначаются как , где
— ширина диаграммы направленности и
— ширина луча половинной мощности, и зависят, как ни трудно догадаться, от характеристик определенных антенных устройств:
- Фазовые эффекты в атмосфере
Если верить классикам, то влияют эти потери в первую очередь на скорость передачи данных, обусловленную шириной полосы пропускания приемника, ибо полосу желательно выбирать в соответствии с таблицей 1 [1, с. 91 ]. Чтобы избежать фазовых искажений.
Таб. 1. Максимальная ширина полосы приемника для разных диапазонов.
| Несущая частота, ГГц | 0.5 | 1 | 5 | 10 |
|---|---|---|---|---|
| Полоса пропускания приемника (B), МГц | 10 | 25 | 270 | 750 |
Хотя, нельзя не отметить, что цифры весьма внушающие и зачастую не рассматриваемые, скорее, по причине шумов тепловых.
- Потери из-за несогласованности поляризации антенн
Можно оценить в зависимости от коэффициентов эллиптичности и (вырезку из советской книжки прилагаю в качестве рисунка 1).
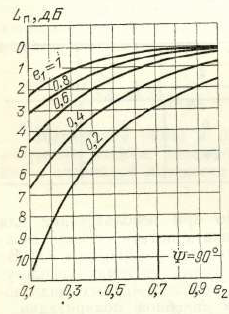
Рис.1. Зависимость потерь из-за несогласованности поляризаций передающей и приемной антенн от эллиптичности. [1, с. 93 ]
Однако попадался мне этот параметр и в качестве справочных данных. Например, в расчете энергобюджета для NanoCom AX100 поляризационные потери составляют 3 дБ (атмосферные потери составляют 2,1 дБ, ионосферные потери составляют 0,4 дБ ).
- Затухание в атмосфере
Этот интересный параметр мы можем оценить либо по рекомендациям МСЭ, либо посчитать самостоятельно. Благо, есть специальные библиотеки, наподобие этой.
Затухания на пути распространения электромагнитной волны (Path Loss)
Не мудрствуя лукаво, применим для начала формулу Фрииcа:
где — длина электромагнитной волны (относится известным образом к несущей частоте
,
— скорость электромагнитной волны (скорость света, если проще)), а
— расстояние между спутниками и наземной станцией.
И здесь мы подходим, пожалуй, к самому интересному вопросу: а какое расстояния взять для расчетов? Как уже было упомянуто во вступлении, рассматриваем мы LEO спутники, а значит относительно Земли наш предполагаемый спутник движется (в отличие от геостационарного случая, при котором спутник, как бы, висит над одной точкой).
Можно, конечно, всё максимально упростить, приняв за основу схему (рис. 2), когда предполагается, что орбита спутника связи пролегает, грубо говоря, "над головой" нашей наземной станции.
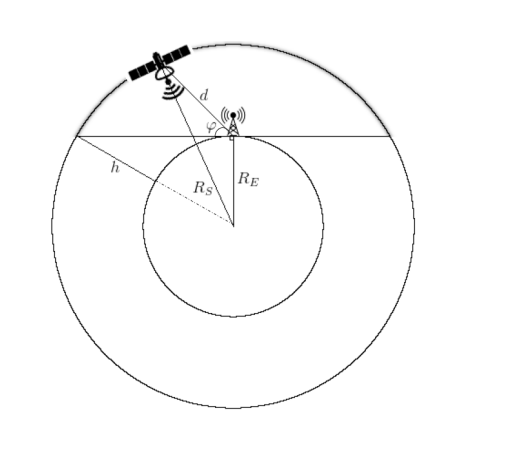
Рис. 2. Схематическое описание траектории CubeSat на низкой околоземной орбите [2].
Тогда расстояние можно посчитать по формуле:
где — есть, собственно, радиус Земли,
— высота орбиты спутника, а
— угол элевации.
Однако, можно запариться ещё немного, обратиться снова к классику (уже к другому) [3, p.110-123] и посчитать всё уже относительно реальных географических координат наземной станции (
и
) и реального положения спутника (мгновенной долготы восходящего узла — instantaneous ascending node
и мгновенного полюса орбиты — instantaneous orbit pole
). Приготовьтесь, будет много тригонометрии:
где — минимальный центральный угол Земли,
— минимальный угол надира,
— угловой радиус Земли. Максимальное расстояние можно рассчитать по:
где и
(
— минимальный угол элевации спутника).
Подведем короткий итог по параметрам:
- Что выбираем в качестве исходных точек: несущую частоту, высоту орбиты (возможно, положение спутника и географические координаты наземной станции — зависит от точности, которую хотим получить);
- Находим зависящие от оборудования и регулируемые параметры: передаваемая мощность, ширина полосы приемника;
- Находим справочные данные: усиления и потери антенны, усиления и потери в фидере, шумовая температура, дополнительные потери.
Промоделируем, что получилось в итоге
В качестве источника технических параметров для оценки нисходящей линии связи нам доступны реальные примеры приемопередатчиков и антенн для спутников CubeSat, такие, как NanoCom AX100 и NanoCom ANT430. Для большей ширины полосы частот лучше, конечно, рассмотреть S-диапазон. Для этого диапазона доступны патч-антенна NanoCom ANT2000 и приемопередатчик NanoCom SR2000.
Начинаем проверять, что получилось.
from SmallSatLB import *
import pandas as pdВся логика условно разделена на две опции: 'draft', при которой для подсчета расстояния используется формула (4); и 'precise', при которой используются формулы (5) и (6).
'draft'
l_d = LinkBudget(750*1e3, 'draft') #инициализируем наш класс (доступен по ссылке выше)
d = l_d.distance() # расчитываем расстояние
phi = np.pi*np.array(range(0,181,5))/180 # задаем диапазон углов элевации
plt.plot(180*phi/np.pi, d*1e-3, '-o')
plt.title('Distances')
plt.xlabel('Elevation angles (degrees)')
plt.ylabel('Distance (km)')
plt.grid() 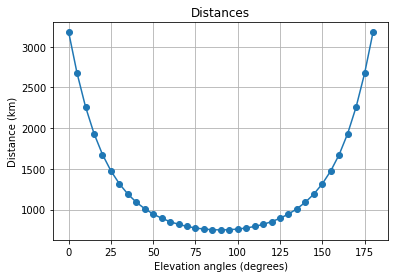
snr, EIRP = l_d.expected_snr(2.4e9, 1, 7.3, 35, 1.5e6, 1000) # считаем SNR
plt.title('Expected SNRs')
plt.xlabel('Elevation angles (degrees)')
plt.ylabel('SNR (dB)')
plt.legend()
plt.grid()
Красота!
'precise'
l_p = LinkBudget(750*1e3, 'precise',\
L_node = 100+90, incl = 90 - 61.5,\
lat_gs = 22, long_gs = 200, eps_min = 5)
snr, EIRP = l_p.expected_snr(2.4e9, 1, 7.3, 35, 1.5e6, 1000)
print(min(snr))
print(max(snr))>>> 5.556823874020452
>>> 8.667000351847676В общем-то вот: есть у нас небольшой инструмент для первичных "прикидок" и расчетов того, насколько ослабнет сигнал, пока будет идти от спутника до Земли (или обратно).
Спасибо всем за внимание!
Список использованной литературы:
- Кантор Л. Я., Аскинази Г. Б. Спутниковая связь и вещание: справочник. – Радио и связь, 1988.
- Otilia Popescuy, Jason S. Harrisz and Dimitrie C. Popescuz, Designing the Communica- tion Sub-System for Nanosatellite CubeSat Missions: Operational and Implementation Perspectives, 2016, IEEE
- Wertz J. R., Larson W. J. Space Mission Analysis and Design, Space Technology Library. – Microcosm Press and Kluwer Academic Publishers, El Segundo, CA, USA,, 1999.





