Всем привет! Я реализовал похоже собственный алгоритм поиска кратчайшего пути с отрицательными ребрами графа.
Почему собственный? Я искал подобное решение, но не нашел, возможно, оно уже было реализовано, просто плохо поискал. Жду Нобелевскую премию =)
Додумался я до него путем модификации классического Дейкстры. Прошу адекватно отнестись к содержимому, ибо это моя первая статья, и, возможно, я ничего не придумывал и, вообще, этот алгоритм не работает вовсе (но по моим тестам он работает правильно).
Повторюсь, алгоритм работает с отрицательными ребрами графа (но не с циклическими отрицательными). Чем этот алгоритм отличается от известного Беллмана-Форда
Сложностью! У известного алгоритма сложность составляет O(n3). У "моего" алгоритма по моим расчетам сложность не превышает оригинальной сложности алгоритма Дейкстры, а именно O(n2). Если это не так, поправьте, пожалуйста, после ознакомления с реализацией на языке Python
Реализация
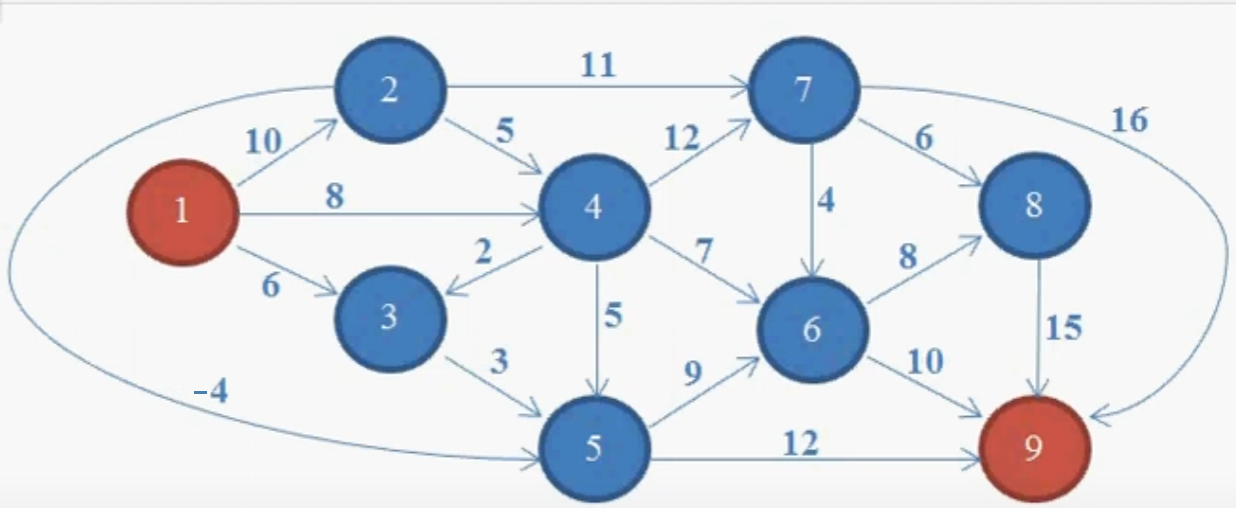
Итак, у нас есть граф с отрицательным ребром между 2-м и 5-м узлом. Наша задача - найти кратчайший путь от источника (1-го узла) до 9-го узла.
Граф будет храниться в виде хэш таблицы, где:
graph = {
нода_1_(источник): {сосед_1: вес до него, сосед_2: вес до него, ...},
нода_2: {сосед_1: вес до него, сосед_2: вес до него, ...},
...
}
graph = {
1: {2: 10, 3: 6, 4: 8},
2: {7: 11, 4: 5, 5: -4},
3: {5: 3},
4: {7: 12, 3: 2, 5: 5, 6: 7},
5: {6: 9, 9: 12},
6: {8: 8, 9: 10},
7: {6: 4, 8: 6, 9: 16},
8: {9: 15},
9: {}
}Важно! Нужно писать узлы графа в порядке их отдаленности от источника. Т.е. сперва описываем первых соседей источника. После того, как описали их, приступаем к следующим соседям соседей. Т.е. описываем поуровнево, будто это не взвешенный граф, а обыкновенное дерево, где реализовываем поиск в ширину. В Python словари являются упорядоченными (начиная с версии 3.6), поэтому нам не стоит прибегать к другим структурам данных, типа Ordered dict из модуля collections.
Можно описать граф матрицей смежностей, но мне так проще.
Так же нам понадобится еще 2 хэш таблицы.
Минимальные веса от источника до этой ноды в виде:
costs = {
нода_1_(источник): 0,
нода_2: infinity,
нода_3: infinity,
...
}
Заполнять и обновлять мы ее будем по мере прохождения по "детям" узлов.
costs = {} # Минимальный вес для перехода к этой ноде (кратчайшие длины пути до ноды от начального узла)Таблица родителей нод, от которых проходит кратчайший путь до этой ноды:
parents = {} # {Нода: его родитель}Ее так же будем заполнять и обновлять по мере прохождения по детям узлов.
Как и в алгоритме Дейкстры, будем отмечать еще неизвестные до узлов расстояния бесконечностью. Инициализируем эту переменную:
infinity = float('inf') # Бесконечность (когда минимальный вес до ноды еще неизвестен)Далее создаем пустое множество. Там будут храниться обработанные узлы (что значит "обработанные", поясню далее, а пока просто создаем множество)
processed = set() # Множество обработанных нодПриступим к самому алгоритму!
Начинаем с источника (первого узла). Смотрим на веса всех его соседей в таблице costs. Путь до них бесконечный, а любое число уже меньше бесконечности, поэтому обновляем веса. Так же вносим родителей всех узлов, т.к. мы обнаружили путь до ноды короче. Когда посмотрели всех соседей, вносим наш рассматриваемый узел в множество обработанных узлов processed (этот узел мы не будем обрабатывать в дальнейшем).
Здесь важный момент и отличие от алгоритма Дейкстры. Мы будем смотреть не минимальный по весу необработанный узел, а смотреть вообще ВСЕХ соседей поочередно. Т.е. у нас есть соседи после первого этапа алгоритма.
Мы поочередно так же будем искать уже их соседей и обновлять минимальные веса. Если же достижимый вес окажется меньше, чем внесенный в таблицу, то мы его заменяем. Так же заменяем его родителя в таблице parents.
Когда посмотрели всех соседей, вносим узел в множество обработанных. Т.е. множество обработанных - это те узлы, у которых мы рассмотрели всех его соседей!И так повторяем поуровнево (не приступаем к соседям соседей, пока не обработаем первых соседей), пока не будут обработаны все узлы.
Код:
graph = {
1: {2: 10, 3: 6, 4: 8},
2: {7: 11, 4: 5, 5: -4},
3: {5: 3},
4: {7: 12, 3: 2, 5: 5, 6: 7},
5: {6: 9, 9: 12},
6: {8: 8, 9: 10},
7: {6: 4, 8: 6, 9: 16},
8: {9: 15},
9: {}
}
parents = {} # {Нода: его родитель}
costs = {} # Минимальный вес для перехода к этой ноде (кратчайшие длины пути до ноды от начального узла)
infinity = float('inf') # Бесконечность (когда минимальный вес до ноды еще неизвестен)
processed = set() # Множество обработанных нод
for node in graph.keys():
if node not in processed: # Если нода уже обработана не будем ее заново смотреть (иначе м.б. беск. цикл)
for child, cost in graph[node].items(): # Проходимся по всем детям
new_cost = cost + costs.get(node,
0) # Путь до ребенка = путь родителя + вес до ребенка (если родителя нет, то путь до него = 0)
min_cost = costs.get(child,
infinity) # Смотрим на минимальный путь до ребенка (если его до этого не было, то он беск.)
if new_cost < min_cost: # Если новый путь будет меньше минимального пути до этого,
costs[child] = new_cost # то заменяем минимальный путь на вычисленный
parents[child] = node # Так же заменяем родителя, от которого достигается мин путь
processed.add(node) # Когда все дети (ребра графа) обработаны, вносим ноду в множество обработанных
print(f'Минимальные стоимости от источника до ноды: {costs}')
print(f'Родители нод, от которых исходит кратчайший путь до этой ноды: {parents}')
# -> Минимальные стоимости от источника до ноды: {2: 10, 3: 6, 4: 8, 7: 20, 5: 6, 6: 15, 9: 18, 8: 23}
# -> Родители нод, от которых исходит кратчайший путь до этой ноды: {2: 1, 3: 1, 4: 1, 7: 4, 5: 2, 6: 4, 9: 5, 8: 6}Мы получили кратчайшие расстояния от источника до каждого достижимого узла в графе, а так же родителей этих узлов. Как же нам построить цепочку интересующего нас пути от источника до 9-ой ноды (либо до любой другой достижимой)? Ответ в коде ниже:
def get_shortest_path(start, end):
'''
Проходится по родителям, начиная с конечного пути,
т.е. ищет родителя конечного пути, потом родителя родителя и т.д. пока не дойдет до начального пути.
Тем самым мы строим обратную цепочку нод, которую мы инвертируем в конце, чтобы получить
истинный кратчайший путь
'''
parent = parents[end]
result = [end]
while parent != start:
result.append(parent)
parent = parents[parent]
result.append(start)
result.reverse()
result = map(str, result) # В случае если имена нод будут числами, а не строками (для дальнейшего join)
print(f'Кратчайший путь от {start} до {end}: {costs[end]}')
return result
shortest_path = get_shortest_path(start=1, end=9)
print('-->'.join(shortest_path))
# -> Кратчайший путь от 1 до 9: 18
# -> 1-->2-->5-->9Итак, мы нашли кратчайший путь до 9 узла, и обратите внимание, он проходит через ребро с отрицательным весом! Т.е. нас теперь не пугает наличие такого ребра, в отличие от оригинальной Дейкстры.
Сложность
В оригинальном алгоритме Дейкстры сложность в худшем случае складывается из
Прохода по всем узлам графа (n)
В этот цикл вложен еще один - поиск минимального не посещенного узла. Он работает за O(n), но можно сделать и за O(Elogn) путем реализации кучи (heapq)
Прохождение по соседям узла. Занимает O(E), где Е - количество ребер в графе. Т.к. это константа, то ее опускают.
Итого алгоритм занимает O(n2+E), а с реализацией кучи, скорость возрастает до O(Elogn) (на самом деле это будет не всегда так, но в большинстве случаев)
Что касается "моего" алгоритма, то если где-то не ошибаюсь:
Проход по всем узлам графа O(n)
Проход по всем соседям O(n)
Обновление весов O(1)
Итого O(n2). Not bad! Что по памяти? costs - O(n), parents - O(n), processed - O(n)
Считаю, неплохо для такого рода алгоритма.
Еще деталь такая. При реализации классической Дейкстры, в случае, когда поиск МИНИМАЛЬНОГО по весу узла совпадет с нашим конечным целевым узлом,
то мы можем прервать дальнейшую обработку, т.к. мы уже нашли кратчайший путь до интересующего узла. В "моем" же алгоритме мы все равно будем обрабатывать все узлы.
Выводы
В случае, если нам могут встретится отрицательные ребра в графе, можно пользоваться данным алгоритмом. Можно воспользоваться и известным Беллмана-Форда, кому как нравится, но мне показался он более сложным в понимании.
В случае, если нам известно, что граф не содержит отрицательных весов, тогда можно смело пользоваться Дейкстрой.
ЕЩЕ РАЗ ПОДЧЕРКИВАЮ!
Я не знаю, был ли этот алгоритм до этого или нет. Может он вообще работает некорректно, но я тестировал его с разными данными, и он работал правильно.
Если будут какие-то поправки или замечания, жду обратную связь. Может быть, реализация вообще работает только с определенными графами, возможно, есть и такие, которые все сломают :)
Всем спасибо, жду Ваше мнение по поводу этой статьи!