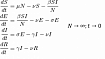Прежде чем перейти к статье, хочу вам представить, экономическую онлайн игру Brave Knights, в которой вы можете играть и зарабатывать. Регистируйтесь, играйте и зарабатывайте!
Определение.
Однородная функция степени q — числовая функция f : R^n → R такая, что для любого v ∈ R^n из области определения функции f и любого λ ∈ R выполняется равенство: f(λv)=λ^q f(v), где q — называется порядком однородности.
Для простоты берем q=1, и рассматриваем функции вида f(a,b)=(a^117-b^117)^(1/117), f(a,b,c,d)=(a^117-b^117)^(1/117)-(c^117-d^117)^(1/117).
После несложных численных расчетов на Python и Java были получены следующие равенства.
f(352,54)=353.99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999...
f(357,59)=356.9999999999999999999999999999999999999999999999999999999999999999999999999999999999999999998972...
f(361,63)=360.999999999999999999999999999999999999999999999999999999999999999999999999999999999999999939...
MS Excel:
f(352,54)=352,000000000001
f(357,59)=357,000000000001
f(361,63)=361,000000000001
Скрипт на Python:
from decimal import *
getcontext().prec = 308
>>> x=(Decimal(352)**Decimal(117)-Decimal(54)**Decimal(117))(Decimal(1)/Decimal(117))
>>> print(x)
351.99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999998329159190818894696994980506790444791082984001875203468391468411917936881307214870551679958590777317468915163628481716135549589884152531038661217609555941316588708754835741185821790242245778320061791986803024655
>>> x=(Decimal(357)**Decimal(117)-Decimal(59)**Decimal(117))(Decimal(1)/Decimal(117))
>>> print(x)
356.99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999989720158196073692153897626133606380322329055537315843030235571925317558982699264816534943225755076027658785035832219023824960424396774347405335963769219643742987625523407845824626821939913224289857224063032843297400
>>> x=(Decimal(361)**Decimal(117)-Decimal(63)**Decimal(117))(Decimal(1)/Decimal(117))
>>> print(x)
360.99999999999999999999999999999999999999999999999999999999999999999999999999999999999999993921127936674583510825707397891980952152159386267417777344776761307280088078727565211233452220813716097076319749507809649466951661213836906215116123352999333771519212777104493376322107139264556222426180333043207111704
Скрипт на Java аналогичен, единственно, отличие в том, что надо найти библиотеку
для присвоения вида: RESULT=BigDecimalMath.root(POWER,RESULT);
Советую взять библиотеку A Java Math.BigDecimal Implementation of Core Mathematical Functions
MS Excel:
f(398,100,398,308)=7.38964445190504E-13
f(398,100,398,309)=7.38964445190504E-13
Скрипт на Python:
>>> x=(Decimal(398)**Decimal(117)-Decimal(100)Decimal(117))(Decimal(1)/Decimal(117))-(Decimal(398)**Decimal(117)-Decimal(309)Decimal(117))(Decimal(1)/Decimal(117))
>>> print(x)
4.6829537694880400495961208753068636086170585442527635529935481848840914660367426890426968518388082410943344799080628343292984538641902867227063198133880387010206424683985254813925375685020961046102263610649485204384515121661567412189563550051412170861083133399095734629020724759126523504592133E-13
>>> x=(Decimal(398)**Decimal(117)-Decimal(100)Decimal(117))(Decimal(1)/Decimal(117))-(Decimal(398)**Decimal(117)-Decimal(308)Decimal(117))(Decimal(1)/Decimal(117))
>>> print(x)
3.2048787849158093680423522610101807533554641830481900686328630295592641185012838297491718621152607396025746152496522964996997085198842879841026218584337924367377107257472526086034104095639711035849133200650433251604302283626496677147152423702885746810118429098239541285725629711670483877984277E-13
Вычисления на Java дают аналогичный результат.
При этом на OneNote получаем 0.
(398^117−100^117 )^(1/117)−(398^117−308^117 )^(1/117)=0.0
(398^117−100^117 )^(1/117)−(398^117−309^117 )^(1/117)=0.0
Более того, зададим большую точность каждого члена разности в OneNote.
f(398,100,398,309)=(15357461407072152272595341560605217489962580453253454782381000698280555150698266871781901372815261064006144084350804830440836948323660592372567223353043470694217100899363125243630508686232896955794063869972410449739272809998037351885263675820458842645745358787039602864806831680779682282811435404889161728-1000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000)^(1/117)-(15357461407072152272595341560605217489962580453253454782381000698280554150698266871781901372815261064006144084350804830440836948323660592372567223353043470694217100899363125243630508686232896955794063869972410449739272809998037351885263675820458842645745358787039602864806831680779682282811435404889161728-2114180645468154536609920593038690001743619316845525182583618652336185889082286837642707603829510005111656415448959134686540978425229790947408474334697737411374763474080732609023460376667948921254970853067562089178774007996892973246633386570133532092567215418841778357322933607577932579981669)^(1/117)=0.0
Что делает его использование непригодным даже для элементарных расчетов.
Однако, рассматривай мы данный пример в Access, то получим:
SELECT (15357461407072152272595341560605217489962580453253454782381000698280555150698266871781901372815261064006144084350804830440836948323660592372567223353043470694217100899363125243630508686232896955794063869972410449739272809998037351885263675820458842645745358787039602864806831680779682282811435404889161728 - 1000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000)^(1/117)-(15357461407072152272595341560605217489962580453253454782381000698280554150698266871781901372815261064006144084350804830440836948323660592372567223353043470694217100899363125243630508686232896955794063869972410449739272809998037351885263675820458842645745358787039602864806831680779682282811435404889161728-2114180645468154536609920593038690001743619316845525182583618652336185889082286837642707603829510005111656415448959134686540978425229790947408474334697737411374763474080732609023460376667948921254970853067562089178774007996892973246633386570133532092567215418841778357322933607577932579981669)^(1/117);
или
SELECT (398^117-100^117)^(1/117)-(398^117-309^117)^(1/117);
с одинаковым результатом f(398,100,398,309)=4,54747350886464E-13.
У MS Word не только своя собственная математика, но и свое понимание вычислений.
Делаем таблицу из одного столбца и вычисляем.
15357461407072152272595341560605217489962580453253454782381000698280555150698266871781901372815261064006144084350804830440836948323660592372567223353043470694217100899363125243630508686232896955794063869972410449739272809998037351885263675820458842645745358787039602864806831680779682282811435404889161728
1000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
A1-A2 = 2,16
15357461407072152272595341560605217489962580453253454782381000698280554150698266871781901372815261064006144084350804830440836948323660592372567223353043470694217100899363125243630508686232896955794063869972410449739272809998037351885263675820458842645745358787039602864806831680779682282811435404889161728
2114180645468154536609920593038690001743619316845525182583618652336185889082286837642707603829510005111656415448959134686540978425229790947408474334697737411374763474080732609023460376667948921254970853067562089178774007996892973246633386570133532092567215418841778357322933607577932579981669
A5-A4=2,14
A3-A6=0,02
Что совсем неверно (а формула A5-A4=2,14, никак и нигде объяснения не находит) .
Резюме такое. Существует множество пар значений однородных функций от двух и четырех переменных, которые вызывают сложности в MS Office 365 Excel, Word, OneNote, но не в Access.