Про настройку гиперпараметров ансамблей моделей машинного обучения

Привет Хабр!

Под катом хочется затронуть тему настройки гиперпараметров в моделях машинного обучения, получаемых при помощи блендинга. В таких ансамблях предсказания из одной модели машинного обучения становятся предикторами для другой (следующего уровня). На рисунке ниже представлены некоторые варианты ансамблей, где данные передаются слева направо. Называть такие ансамбли мы будем в рамках поста также пайплайнами или композитными моделями (композитные пайплайны). 

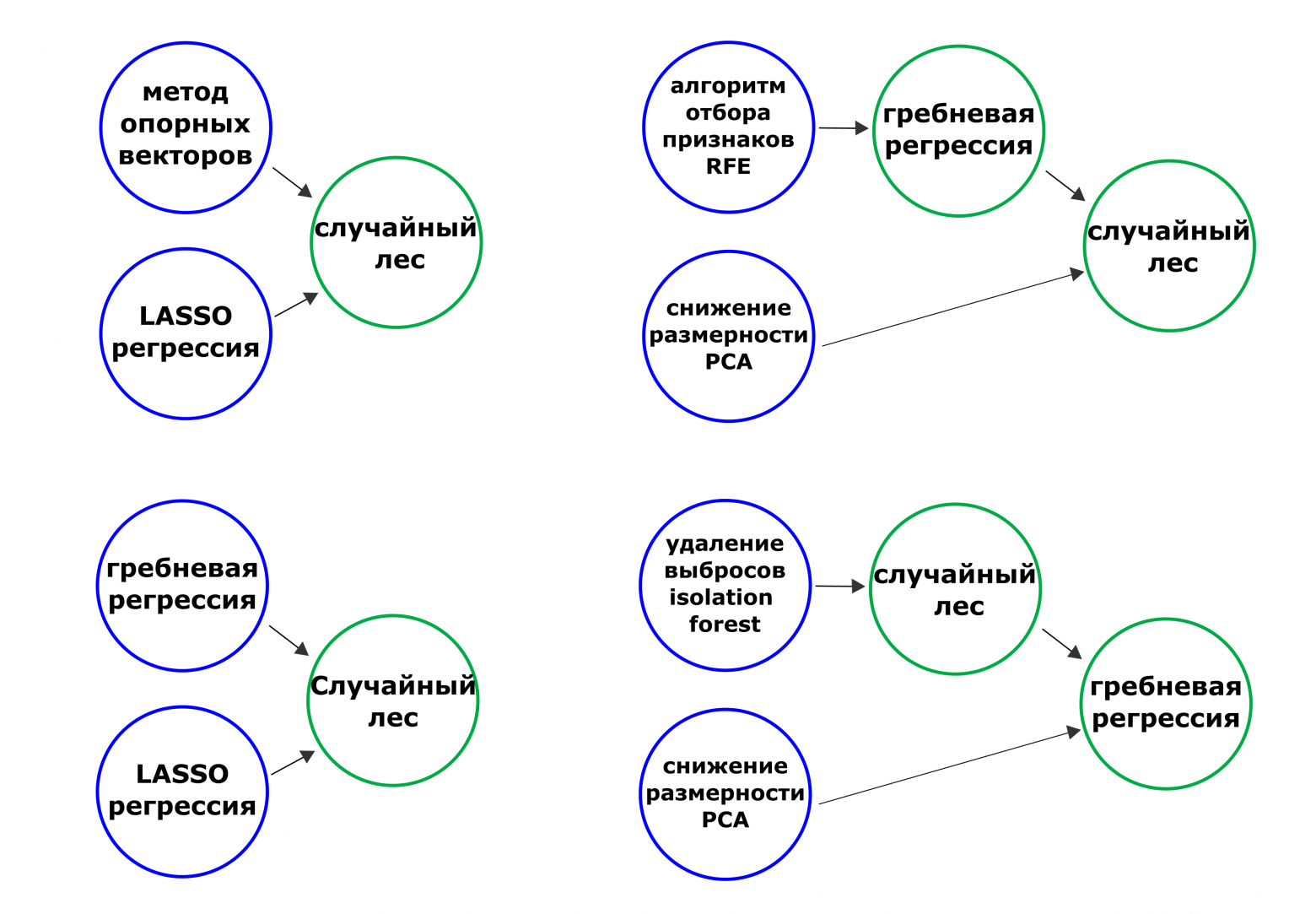
От использования таких сложных композитных структур может уменьшаться ошибка прогноза. Модели иногда становятся более робастными. Однако, существует и обратная сторона - за высокую эффективность приходится платить “прожорливостью ансамбля” (времени и вычислительных ресурсов на ансамбль тратится гораздо больше, чем для одиночных моделей). Также чем сложнее пайплайн, тем сложнее его настраивать. Вот про то, как можно в таких ансамблях производить настройку гиперпараметров мы и поговорим. 

Дисклеймер: мы не обсуждаем конкретные методы оптимизации, например байесовскую оптимизацию, случайный поиск, или эволюционные алгоритмы (или какие-либо ещё алгоритмы). Здесь обсуждаются более верхнеуровневые подходы к настройке гиперпараметров независимо от алгоритмов, используемых в ядре. В примерах из данного поста используется байесовская оптимизация при помощи библиотеки hyperopt, однако она может быть заменена на более подходящую (вам или нам) при необходимости. 

Как эту задачу решают в свободной индустрии

Очевидно, очень по-свободному. 

Ну достаточно шуток, русскоязычных материалов на тему подготовки ансамблей из моделей машинного обучения относительно немного. Начать, полагаю, стоит с “Cтекинг (Stacking) и блендинг (Blending)”. Затем продолжим изучение темы с “Построение ансамблей моделей” и “Машинное обучение: ансамбль смешивания на Python” (тут настройка кстати гиперпараметров не производится), заглянем в англоязычный интернет и, наконец, пробежимся по готовым решениям победителей и участников kaggle соревнований. 

Из работ выше можем резюмировать следующий классический подход. Сначала обучаются и настраиваются все одиночные модели первого уровня, - затем уже ансамблирующая модель (модели). Затем процесс повторяется, получается такое итеративное продвижение слева направо. Такой же подход эксплуатируется в “Hyperparameter Tuning the Weighted Average Ensemble in Python”, где настраиваются только веса ансамбля. 

В тетрадке с kaggle “A Data Science Framework: To Achieve 99% Accuracy” система такая же: гиперпараметры настраиваются у каждой модели по отдельности. Тем не менее даже кагглеры-чемпионы отмечают, что настраивать гиперпараметры в ансамблях, дело тем не менее нетривиальное: “We could have experimented with more hyperparameters in our detection models as well. I really dislike hyperparameter tuning (never really developed a good strategy for it) and often try and compensate by ensembling different models together.” © [1st place] Solution Overview & Code.

Как эту задачу решают в душной академии

Очевидно, очень по-душному.

Вот где информации и подходов навалом, так это в научных статьях, в которых ещё и как правило не имеется ни ссылок на программные реализации алгоритмов, ни на репозиторий с экспериментами. Еще заметим, что информации из отечественных статей на эту тему найти не удалось (честно, всю первую страницу поиска в google scholar протыкал - ничего не нашёл), поэтому сразу перейдём к англоязычным источникам. 

Достойным упоминания сочтём подход “ничего не делать” - при таком подходе веса у ансамбля (если это взвешенное ансамблирование) не настраиваются вовсе. Все модели первого уровня включаются в ансамбль с одинаковыми весами. Однако, такой метод не всегда оптимальный (см. Stacked ensemble combined with fuzzy matching for biomedical named entity recognition of diseases). Естественно, данный подход нельзя отнести к методам настройки гиперпараметров, поэтому перейдём к настоящим методам. 

Начнем с классического подхода “сначала настраивается каждая модель по отдельности, затем - веса у ансамбля”. Такой подход описан, например в Optimizing ensemble weights and hyperparameters of machine learning models for regression problems, где его оптимальность, стоит заметить, подвергается сомнению. Собственно, даже в рамках этой статьи авторы предлагают более перспективную альтернативу - настраивать гиперпараметры моделей и веса ансамбля одновременно. 

В Hyperparameters tuning of ensemble model for software effort estimation используется точно такой же подход, только обобщенный для стекинга, когда финальные предсказания объединяются не взвешиванием, а моделью. Поскольку пространство поиска получилось в их случае достаточно большим, для оптимизации использовались метод роя частиц и генетический алгоритм.

В целом встречается довольно много вариаций на описанные выше несколько подходов, но принципиально разных методов всего два: настройка базовых моделей по отдельности и настройка всех моделей в ансамбле одновременно. 

Какие подходы мы в итоге выделили

Отметим, что все вышеперечисленные изыскания мы проводили для того, чтобы улучшить модуль настройки гиперпараметров в нашем open-source AutoML фреймворке FEDOT. Такой типичный пример работы R&D: мы хотели улучшить модуль настройки гиперпараметров и нужно было выбрать один, самый подходящий подход. В таком случае нужно 1) определить конкурирующие решения, 2) реализовать прототипы подходов, 3) провести оценку и 4) выбрать лучший (по заданным критериям) и 5) интегрировать выбранный подход в проект.. Когда мы провели обзор подходов, мы реализовали в рамках выбранной ветки три подхода к настройке гиперпараметров. А затем провели эксперименты с целью определения наиболее удачного подхода. Критерии успешности подхода выделим для начала два: алгоритм настройки должен работать быстро и точно, то есть ошибка ансамбля после настройки гиперпараметров должна быть меньше, чем с параметрами по умолчанию.

Не будем тянуть интригу - каких же трёх красавцев мы приготовили (названия придуманы автором):

• изолированная настройка;

• последовательная;

• одновременная.

Обсудим теперь каждую стратегию в отдельности. Для большей наглядности будем использовать анимации. Первой пойдёт изолированная (Анимация 1). 

Красным цветом подсвечиваются узлы, в которых производится настройка гиперпараметров и стрелками показано, через какие узлы передаются данные. Из анимации видно, что на каждой итерации настраивается только один узел. При этом метрика ошибки измеряется по предсказаниям, получаемых из данного узла. Это означает, что на одной итерации данные передаются только через узлы-предки настраиваемой модели. При такой стратегии соблюдается принцип “одна итерация - обучение одной модели”. 

Теперь перейдём к аналитике. К плюсам приведенного подхода относится вычислительная эффективность. Действительно, на каждой итерации не требуется обучать все модели пайплайна заново. 

Но ключевыми являются именно недостатки. Первый и самый главный, это узкоспециализированность алгоритма - он работает только на тех узлах, вывод которых можно сопоставить с целевой переменной и получить метрику, то есть только на моделях. Если в структуре пайплайна присутствуют операции предобработки (например алгоритм отбора признаков, или снижается методом главных компонент), то применить данный подход невозможно. Раз вывод некоторых узлов невозможно напрямую сопоставить с целевой переменной для оценки ошибки, то такие операции настроить не получится. Решить эту проблему можно отчасти решить при помощи включения дополнительных правил: например можно игнорировать такие случаи, или настраивать гиперпараметры предобработок совместно с параметрами моделей-потомков. Однако данные модификации требуют времени на внедрение, поэтому мы их решили отложить до того момента, пока не убедимся, что подход является наиболее перспективным - прототип обошелся без этого.  

Вторым минусом является специфика самого подхода. Алгоритм то - жадный. Мы на каждом шаге занимаемся тем, что пытаемся получить локально оптимальную конфигурацию гиперпараметров для каждого подграфа большого пайплайна. Нет никаких гарантий, что в погоне за оптимумом на каждом шаге мы не проскочим глобальный для всего пайплайна.  

Недостатки первого подхода (хотя бы некоторые из них) может решить второй - последовательная настройка (Анимация 2).

В данном подходе данные пропускаются уже целиком через весь пайплайн на каждой итерации (красные стрелочки светятся у всего пайплайна), хотя по прежнему оптимизируются гиперпараметры только у одной операции. 

Плюсы подхода: 

• Возможность оптимизировать пайплайн любой структуры, в том числе содержащий операции предобработки;

• На каждой итерации сопоставляются вывод композитной модели целиком. Следовательно, модель оптимизируется по финальным, а не промежуточным предсказаниям. 

Но есть и минусы. Поскольку мы начинаем идти справа налево, то получается, что во время оптимизации гиперпараметры предшествующих моделей подстраиваются под одну конфигурацию последующих (потомков). А уже на следующем узле, конфигурация потомка меняется на новую. Возможно, это и не самая большая проблема, ведь всегда можно оставить исходные значения гиперпараметров у узлов-потомков, если любые другие сочетания не приводят к улучшению метрики. 

Однако продвигаясь последовательно мы сужаем пространство поиска, поскольку прошедшие ранее оптимизацию узлы не могут уже изменять назначенные гиперпараметры. Таким образом мы сами можем себя загнать себя в “неоптимальный угол” и несмотря на то, что оптимизировать финальную ансамблирующую модель мы ещё можем, ничего улучшить не выйдет. Мне в голову приходит аналогия с тортом, который люди передают по цепочке, откусывая при этом по кусочку. Последнему в этой очереди может ничего не достаться - хотя именно он, возможно, мог раскрыть секрет его приготовления и тогда не пришлось бы никогда стоять в очереди за тортами... 

Коллеги: Как же преодолеть проблемы предыдущих подходов?

Я: Да просто сгрузим всё в кучу!

Так и поступили. На Анимации 3 показано, что можно оптимизировать весь пайплайн как один большой “черный ящик”, где набор гиперпараметров пайплайна равен объединению наборов параметров моделей в его структуре. 

Плюсы: 

• Оптимизируется значение метрики для всего пайплайна целиком;

• В ходе оптимизации пространство поиска не уменьшается - есть возможность одновременно менять гиперпараметры как у корневой модели, так и у предшествующих;

Минусы, вытекающие из преимуществ подхода: 

• Самый вычислительно дорогой способ;

• Очень большое пространство поиска, особенно для больших разветвленных ансамблей.

В общем, третий подход кажется наиболее эффективным для задачи нахождения оптимальных сочетаний гиперпараметров в ансамбле, - проверим это!

Эээксперименты

Итак, выберем наиболее подходящий подход для его внедрения. Для этого поставим эксперимент следующим образом (Таблица 1). Важное уточнение: финальные метрики измеряются на отложенной выборке, к которой тюнер не имел доступ во время оптимизации. 

Таблица 1. Постановка эксперимента. Поскольку Байесовская оптимизация может на разных запусках сходиться к разным решениям, запуски повторяются по 30 раз, чтобы получить более достоверные результаты как по метрикам, так и по времени работы

Сразу отметим, что под термином “ROC AUC” имеется в виду площадь под ROC AUC кривой. На картинке ниже (Рисунок 2) показаны три пайплайна различной разветвленности, которые участвовали в экспериментах.

Количество операций (моделей) в структуре пайплайнов варьировалось от двух (пайплайн A) до десяти (пайплайн C). Расшифровка названий моделей: ridge - гребневая регрессия, lasso - LASSO регрессия, knnreg - K-ближайших соседей для задачи регрессии, svr - метод опорных векторов для задачи регрессии, rfr - случайный лес для регрессии, dtreg - решающее дерево для задачи регрессии, knn -K-ближайших соседей для задачи классификации, rf - случайный лес для классификации, dt - решающее дерево для задачи классификации.

Результаты эээкспериментов

Как мы и писали выше, сравнение будет производиться по двум критериям: время работы и метрики на отложенной выборки. С метрикой на отложенной выборке также введем дополнительный критерий - чем более стабильный (по 30 запускам) результат будет получен, тем метод предпочтительней. То есть будем смотреть не только на среднее значение метрики, но и на разброс. Помимо этого мы также посмотрим на каких типах пайплайнах рассматриваемые подходы работают лучше: на простых линейных A; относительно простых, но разветвленных B, и на сложных многоуровневых C. Также сделаем выводы о том, влияют ли объем выделяемых вычислительных ресурсов (определяется количеством итераций) на эффективность подхода.

Важная оговорка. Поскольку нам не интересно насколько хорошо могут прогнозировать пайплайны типов A, B или C, а перед нами стоит задача выяснить эффективность алгоритмов настройки параметров, то ниже мы будем говорить о приросте в метриках (а не абсолютных значениях). Для симметричной абсолютной процентной ошибки (SMAPE) дельта будет рассчитываться как разность между значением метрики до тюнинга и значением метрики после. Для классификации будем вычитать из метрики после тюнинга метрику до настройки гиперпараметров. Таким образом, для всех задач будет справедливо утверждение “чем больше дельта, тем лучше алгоритм”. 

Дисклеймер: приведенные ниже выкладки не тянут на полноценное научное исследование, а проводились в будничном режиме в процессе разработки. Подобный бенчмаркинг применялся нами при прототипировании. Поэтому, если захотите написать научную статью в Q1-журнал на подобную тему, экспериментов придется провести несколько больше: и метрик рассчитать придётся побольше, и датасетов взять  штук эдак 10-15 для каждой задачи, формализовать гипотезу, провести статистическое тестирование и т.д.

Итак, результаты сравнения улучшения по метрикам для задачи регрессии представлены на Рисунке 3.

На рисунке каждое облако точек представляет собой выборку из тридцати запусков, то есть по тридцать запусков для каждого типа пайплайна (A, B, C), для каждого подхода (изолированный, последовательный, одновременный), для каждого датасета (три регрессионных) и для двух вариантов выделяемого количества итераций для оптимизации (20 и 100). Всего 1620 запусков модуля тюнинга для регрессии, и столько же для классификации. 

Из общей картины сразу выбиваются результаты на датасете “pol”. Действительно, в подавляющем большинстве случаев настройка гиперпараметров приводила к ухудшению прогнозирования на отложенной выборке. Что ж, даже в случае, когда настройка гиперпараметров приводит в конечном итоге к увеличению ошибки прогноза все равно лучше выбрать такой алгоритм, который вредит меньше остальных. 

Если же рассмотреть более “адекватные” запуски, видно, что в среднем одновременная настройка позволяет добиться более стабильно высокого результата: разброс значений меньше, а само облако располагается выше конкурентов. 

Ещё одно наблюдение: в экспериментах используются пайплайны разной степени разветвленности, или сложности, по другому. Из Рисунка 3 видно, что как правило, чем сложнее пайплайн, тем больше пространство поиска для его настройки, и тем более существенный прирост метрики возможно получить. 

На Рисунке 4 показаны результаты для классификационных датасетов. 

В общем, для классификации результаты такие же, как и для регрессии, вырисовывается победитель по приросту метрик и по разбросу таковых - одновременная настройка гиперпараметров. 

Теперь рассмотрим более пристально некоторые случаи, а именно запуски по 20 итераций (Рисунок 5) для таблиц “Amazon_employee_access” (классификация) и “cal_housing” (регрессия). 

Что же на рисунке видно? - Первое, заметно, что в случае с классификацией выборки улучшений метрики постепенно сползают “вправо” при движении в порядке изолированная настройка - последовательная настройка - одновременная. Это говорит о том, что одновременный подход позволяет лучше подбирать гиперпараметры, чем последовательный, а уже он, в свою очередь, надежней, чем изолированная настройка. Также видно, что только третий подход позволяет добиться стабильного улучшения метрики - при использовании других алгоритмов это не гарантировано.

Теперь рассмотрим распределения для пайплайна C при решении задачи регрессии: видно, что только в случае с одновременной настройкой выделяется один заметный высокий пик (мода) у распределения. В остальных двух случаях распределения либо не унимодальны (изолированная настройка), либо растянуты почти по всей оси абсцисс. То есть только в случае с одновременной настройкой удалось добиться высокой скученности результатов, что говорит о том, что если мы применим третий подход, то скорее всего получим такой же высокий результат, как и при прошлом запуске.

Теперь заценим время работы подходов на примере таблиц для регрессии на графике “violin plot” (Рисунок 6). На таком графике по бокам относительно центральной оси каждого элемента откладываются ядерные оценки плотности распределения. Таким образом места расширений у таких “скрипок” показывают моду выборки. 

Начнем с очевидного: чем больше итераций выделяется, тем дольше работает алгоритм. Теперь обратим внимание, что, как и предполагалось, изолированная настройка оказалась существенно более быстрым алгоритмом. 

Однако заметим, что в случае последовательной настройки есть возможность для существенного улучшения. Все операции в пайплайне, которые в данную итерацию не обучаются с новыми гиперпараметрами и при этом не зависят от конфигурируемой модели (например, расположены в пайплайне перед таковой), можно не обучать, а просто вызывать метод predict у уже обученной модели. Действительно, ведь предикторы неизменны, гиперпараметры модели тоже не менялись - значит можно такую операцию поместить в кэш и доставать только для формирования прогноза. В случае с одновременной настройкой гиперпараметров возможности провести подобную модификацию нет. 

Ну и раз мы дошли до финала, предлагаю подвести итог в виде сводной таблички с метриками (Таблица 2).

Таблица 2. Прирост метрики в процентах относительно исходной конфигурации. Показаны значения среднеквадратического отклонения. Не приводятся значения для регрессионного датасета “pol”. Полужирным начертанием показаны результаты лучшего подхода в каждом случае.

Заключение

В данной статье мы рассмотрели какие существуют способы настройки гиперпараметров в ансамблях из моделей машинного обучения. Чтобы определиться какой из выделенных нами трёх подходов наиболее перспективный, мы сделали прототипы каждого подхода. Затем поставили эксперименты на шести набора данных. 

Выводы такие: одновременная настройка позволяет достичь большего прироста метрики и при этом позволяет добиваться такого прироста более стабильно. Наиболее быстрым (по среднему времени выполнения) оказался изолированный подход. Последовательная настройка оказалась в среднем эффективнее изолированной, но при этом хуже одновременной. Однако время выполнения последовательной настройки можно уменьшить, используя кэширование операций. 

P.S. У нас в фреймворке FEDOT мы всё-таки решили реализовать и поддерживать одновременную и последовательную настройку. По умолчанию при тюнинге используется одновременная. 

Полезные ссылки: 

• Репозиторий open-source AutoML фреймворка FEDOT 

• Канал NSS Lab — анонсы наших новых статей и выступлений, посвященных AI/ML

В исследовательской задаче по гиперпараметрам и AutoML разбирались вместе с читателями Сарафанов Михаил и команда NSS lab