Python, наука о данных и выборы: часть 4

Пост №4 для начинающих посвящен техническим приемам визуализации данных.

Важность визуализации

Простые приемы визуализации, подобные тем, которые были показаны ранее, позволяют лаконично передать большое количество информации. Они дополняют сводные статистики, которые мы рассчитали ранее в этой главе, и поэтому очень важно уметь ими пользоваться. Такие статистики, как среднее значение и стандартное отклонение, неизбежно скрывают много информации по той причине, что сворачивают последовательность в одно единственное число.

Английский математик Фрэнсис Энскомб составил коллекцию из четырех точечных графиков, ныне известную как квартет Энскомба, которые обладают практически идентичными статистическими свойствами (включая среднее, дисперсию и стандартное отклонение). Несмотря на это, они четко показывают, что распределение значений последовательностей  и  сильно расходится:

При этом наборы данных не должны быть подстроенными, потому как ценные аналитические выводы будут непременно выявлены при построении графиков. Возьмем для примера гистограмму оценок, полученных выпускниками по национальному экзамену на аттестат зрелости в Польше в 2013 г.:

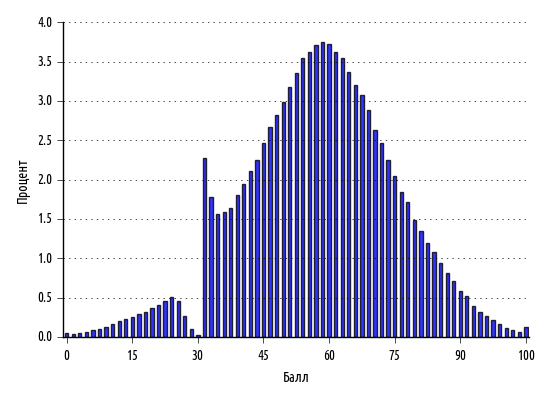
Способности учащихся вполне ожидаемо должны быть нормально распределены, и действительно — за исключением крутого всплеска вокруг 30% — так и есть. То, что мы ясно наблюдаем — это результат по-человечески понятного натягивания экзаменаторами оценок учащегося на проходной балл.

На самом деле статистические распределения для последовательностей, взятых из крупных выборок, могут быть настолько надежными, что даже незначительное отклонение от них может являться свидетельством противоправной деятельности. Закон Бенфорда, или закон первой цифры, показывает любопытную особенность случайных чисел, которые генерируются в широком диапазоне. Единица появляется в качестве ведущей цифры примерно в 30% случаев, в то время как цифры крупнее появляется все реже и реже. Например, девятка появляется в виде первой цифры менее чем в 5% случаев.

^{Закон Бенфорда назван в честь физика Фрэнка Бенфорда (Frank Benford), который сформулировал его в 1938 г., показав его состоятельность на различных источниках данных. Проявление этого закона было ранее отмечено американским астрономом Саймоном Ньюкомом (Simon Newcomb), который еще более 50 лет назад до него обратил внимание на страницы своих логарифмических справочников: страницы с номерами, начинавшихся с цифры 1, имели более потрепанный вид.}

Бенфорд показал, что его закон применяется к самым разнообразным данным, таким как счета за электричество, адреса домов, цены на акции, численность населения, уровень смертности и длины рек. Для наборов данных, которые охватывают большие диапазоны значений, закон настолько состоятелен, что случаи отклонения от него стали принимать в качестве подтверждающих данных в судебной практике по финансовым махинациям.

Визуализация данных об электорате

Вернемся к данным выборов и сравним электоральную последовательность, которую мы создали ранее, относительно теоретической нормальной ИФР. Для создания нормальной ИФР из последовательности значений можно воспользоваться функцией sp.random.normal библиотеки SciPy, как уже было показано выше. Среднее значение и стандартное отклонение по умолчанию равны соответственно 0 и 1, поэтому нам нужно предоставить измеренные среднее значение и стандартное отклонение, взятые из электоральных данных. Эти значения для наших электоральных данных составляют соответственно 70150 и 7679.

Ранее в этой главе мы уже генерировали эмпирическую ИФР. Следующий ниже пример просто сгенерирует обе ИФР и выведет их на одном двумерном графике:

def ex_1_24():
    '''Показать эмпирическую и подогнанную ИФР 
       электората Великобритании'''
    emp      = load_uk_scrubbed()['Electorate']
    fitted   = stats.norm.rvs(emp.mean(), emp.std(ddof=0), len(emp))
    df  = empirical_cdf(emp)
    df2 = empirical_cdf(fitted)
    ax  = df.plot(0, 1, label='эмпирическая')    
    df2.plot(0, 1, label='подогнанная', grid=True, ax=ax)    
    plt.xlabel('Электорат')
    plt.ylabel('Вероятность')
    plt.legend(loc='best')
    plt.show()

Приведенный выше пример создаст следующий график:

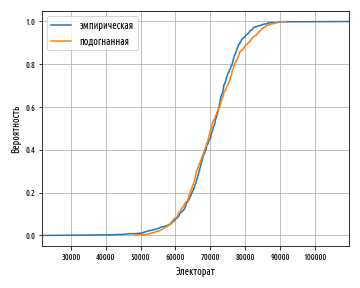
Несмотря на наличие незначительной асимметрии, близкая расположенность двух кривых друг к другу говорит о нормальности исходных данных. Асимметрия выражена в противоположном направлении относительно построенной ранее кривой ИФР нечестного булочника, то есть наши данные об электорате слегка смещены влево.

Поскольку мы сравниваем наше распределение с теоретическим нормальным распределением, то можно воспользоваться квантильным графиком, который делает это по умолчанию:

def ex_1_25():
    '''Показать квантильный график 
       электората Великобритании'''
    qqplot( load_uk_scrubbed()['Electorate'] )
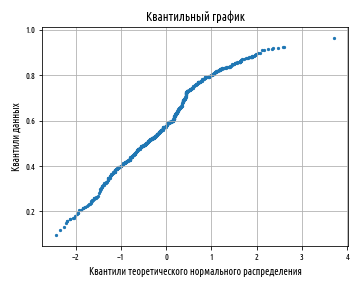
    plt.show()

Следующий ниже квантильный график еще лучше показывает левую асимметрию, с очевидностью присутствующую в данных:

Как мы и ожидали, кривая изгибается в противоположном направлении по отношению к построенному ранее в этой главе квантильному графику нечестного булочника. Это свидетельствует о том, что число более мелких избирательных округов на самом деле больше, чем можно было бы ожидать, если бы данные были более тесно нормально распределены.

Добавление производных столбцов

В целях выяснения процента электората, который проголосовал за одну из двух партий, требуется вычислить сумму голосов, отданных за каждую из них. Для этого нам понадобится создать новое поле данных Victors (Победители) из данных, которые соответствуют Консервативной (Con) и Либерально-демократической (LD) партиям и заодно проверим, имеются ли пропущенные значения.

def ex_1_26():
    '''Вычислить производное поле данных "Победители" и 
       число имеющихся в нем пропущенных значений'''
    df = load_uk_scrubbed()
    df['Победители'] = df['Con'] + df['LD']
    freq = Counter(df['Con'].apply( lambda x: x > 0 ))
    print('Поле "Победители": %d, в т.ч. пропущено %d' 
          % (freq[True], freq[False]))

Поле "Победители": 631, в т.ч. пропущено 19

Результат показывает, что в 19 случаях данные отсутствуют. Очевидно, что в каком-то из столбцов: столбце Con либо столбце LD (либо обоих), данные отсутствуют, но в каком именно? Снова воспользуемся словарем Counter, чтобы увидеть масштаб проблемы:

'''Проверить пропущенные значения в полях
   "Консервативная партия" (Con) и 
   "Либерально-демократическая партия" (LD)'''
df = load_uk_scrubbed()
Counter(df['Con'].apply(lambda x: x > 0)), 
    Counter(df['LD'].apply(lambda x: x > 0))

(Counter({False: 19, True: 631}), Counter({False: 19, True: 631}))

В обоих случаях будет выведено одинаковое число строк, в которых значения есть, и в которых они отсутствуют. Воспользуемся предикативной функцией isnull, которую мы уже встречали ранее в этой главе, чтобы узнать, какие строки не содержат значений:

def ex_1_27():
    '''Выборка полей данных по условию, что поля
       "Консервативная партия" (Con) и 
       "Либерально-демократическая" (LD) не пустые'''
    df   = load_uk_scrubbed()
    rule = df['Con'].isnull() & df['LD'].isnull()
    return df[rule][['Region', 'Electorate', 'Con', 'LD']]

Небольшое обследование данных должно определить причину, почему эти поля оказались пустыми. Как оказалось, кандидаты в соответствующих избирательных округах не выдвигались. Следует ли эти строки отфильтровать или же оставить как есть, равными нулю? Это интересный вопрос. Давайте их отфильтруем, поскольку вообще-то невозможно, чтобы в этих округах избиратели выбрали какого-либо кандидата, неважно от либеральных демократов или консерваторов. Если же мы напротив допустили, что они равны нулю, то среднее количество людей, которое — при заданных вариантах выбора — проголосовало за одну из этих партий, было бы искусственно занижено.

Зная, как фильтровать проблемные строки, теперь добавим производные столбцы, которые будут представлять победителя, долю голосов за победителя и явку на выборы. Отфильтруем строки так, чтобы показать только те, где были выдвинуты кандидаты от обеих партий:

def load_uk_victors():
    '''Загрузить данные по Великобритании, 
       выбрать поля и отфильтровать'''
    df = load_uk_scrubbed()
    rule = df['Con'].notnull()
    df   = df[rule][['Con', 'LD', 'Votes', 'Electorate']] 
    df['Победители']       = df['Con']        + df['LD'] 
    df['Доля победителей'] = df['Победители'] / df['Votes'] 
    df['Явка']             = df['Votes']      / df['Electorate']
    return df

В результате в нашем наборе данных теперь имеется три дополнительных столбца: Victors, Victors Share и Turnout, т.е. победители, доля победителей и явка на выборы. Покажем на квантильном графике долю голосов за победителя, чтобы увидеть, как она соотносится с теоретическим нормальным распределением:

def ex_1_28():
    '''Показать квантильный график победителей 
       на выборах в Великобритании'''
    qqplot( load_uk_victors()['Доля победителей'] )
    plt.show()

Приведенный выше пример создаст следующий ниже график:

Основываясь на сводном графике разных форм кривых квантильных графиков, показанном ранее в этой главе, можно заключить, что доля голосов, отданных за победителя, имеет "легкие хвосты" по сравнению с нормальным распределением. Это означает, что ближе к среднему значению расположено больше данных, чем можно было бы ожидать, исходя из действительно нормально распределенных данных.

Следующая заключительная часть, часть 5, серии постов «Python, наука о данных и выборы» посвящена сопоставительной визуализации электоральных данных.