Разработка динамических древовидных диаграмм с использованием SVG и Vue.js

Материал, перевод которого мы сегодня публикуем, посвящён процессу разработки системы визуализации динамических древовидных диаграмм. Для рисования кубических кривых Безье здесь используется технология SVG (Scalable Vector Graphics, масштабируемая векторная графика). Реактивная работа с данными организована средствами Vue.js.

Вот демо-версия системы, с которой можно поэкспериментировать.


Интерактивная древовидная диаграмма

Комбинация мощных возможностей SVG и фреймворка Vue.js позволила создать систему для построения диаграмм, которые основаны на данных, интерактивны и поддаются настройке.

Диаграмма представляет собой набор кубических кривых Безье, начинающихся в одной точке. Кривые заканчиваются в различных точках, равноудалённых друг от друга. Их конечное положение зависит от данных, введённых пользователем. В результате диаграмма оказывается способной реактивно реагировать на изменения данных.

Сначала мы поговорим о том, как формируются кубические кривые Безье, потом разберёмся с их представлением в координатной системе элемента <svg>, попутно поговорив о создании масок для изображений.

Автор материала говорит, что она подготовила к нему множество иллюстраций, стремясь сделать его понятным и интересным. Цель материала заключается в том, чтобы помочь всем желающим получить знания и навыки, необходимые для разработки собственных систем построения диаграмм.

SVG

▍Как формируются кубические кривые Безье?

Кривые, которые используются в этом проекте, называются кубическими кривыми Безье (Cubic Bezier Curve). На следующем рисунке показаны ключевые элементы этих кривых.


Ключевые элементы кубической кривой Безье

Кривая описывается четырьмя парами координат. Первая пара (x0, y0) — это начальная опорная точка (anchor point) кривой. Последняя пара координат (x3, y3) — это конечная опорная точка.

Между этими точками можно видеть так называемые управляющие точки (control point). Это — точка (x1, y1) и точка (x2, y2).

Расположение управляющих точек по отношению к опорным точкам определяет форму кривой. Если бы кривая была бы задана только начальной и конечной точкой, координатами (x0, y0) и (x3, y3), то эта кривая выглядела бы как прямой отрезок, расположенный по диагонали.

Теперь воспользуемся координатами четырёх вышеописанных точек для построения кривой средствами SVG-элемента <path>. Вот синтаксическая конструкция, используемая в элементе <path> для построения кубических кривых Безье:

<path D="M x0,y0  C x1,y1  x2,y2  x3,y3" />

Буква с, которую можно увидеть в коде — это сокращение для Cubic Bezier Curve. Строчная буква (c) означает использование относительных значений, прописная (C) — использование абсолютных значений. Я для построения диаграммы использую абсолютные значения, на это указывает прописная буква, использованная в примере.

▍Создание симметричной диаграммы

Симметрия — это ключевой аспект данного проекта. Для построения симметричной диаграммы я использовала всего одну переменную, получая на её основе такие значения, как высота, ширина или координаты центра некоего объекта.

Назовём эту переменную size. Так как диаграмма ориентирована горизонтально — переменную size можно рассматривать как всё горизонтальное пространство, которое доступно диаграмме.

Назначим этой переменной реалистичное значение. Будем использовать это значение для вычисления координат элементов диаграммы.

size = 1000

Нахождение координат элементов диаграммы

Прежде чем мы сможем найти координаты, необходимые для построения диаграммы, нам нужно разобраться с координатной системой SVG.

▍Координатная система и viewBox

Атрибут элемента <svg> viewBox весьма важен в нашем проекте. Дело в том, что он описывает пользовательскую координатную систему SVG-изображения. Проще говоря, viewBox определяет позицию и размеры того пространства, в котором будет создаваться SVG-изображение, видимое на экране.

Атрибут viewBox состоит из четырёх чисел, задающих параметры координатной системы и следующих в таком порядке: min-x, min-y, width, height. Параметры min-x и min-y задают начало пользовательской системы координат, параметры width и height — задают ширину и высоту выводимого изображения. Вот как может выглядеть атрибут viewBox:

<svg viewBox="min-x min-y width height">...</svg>

Переменная size, которую мы описали выше, будет использоваться для управления параметрами width и height этой координатной системы.

Позже, в разделе про Vue.js, мы привяжем viewBox к вычисляемому свойству для указания значений width и height. При этом в нашем проекте свойства min-x и min-y всегда будут установлены в 0.

Обратите внимание на то, что мы не используем атрибуты height и width самого элемента <svg>. Мы установим их в значения width: 100% и height: 100% средствами CSS. Это позволит нам создать SVG-изображение, которое гибко подстраивается под размер страницы.

Теперь, когда пользовательская координатная система готова к рисованию диаграммы, давайте поговорим об использовании переменной size для вычисления координат элементов диаграммы.

▍Неизменные и динамические координаты

Концепция диаграммы

Окружность, в которой выводится рисунок, является частью диаграммы. Именно поэтому важно включать её в расчёты с самого начала. Давайте, опираясь на вышеприведённую иллюстрацию, выясним координаты для окружности и для одной экспериментальной кривой.

Высота диаграммы делится на две части. Это — topHeight (20% от size) и bottomHeight (оставшиеся 80% от size). Общая ширина диаграммы делится на 2 части — длина каждой из них составляет 50% от size.

Это делает вывод параметров окружности не требующим особых пояснений (тут используются показатели halfSize и topHeight). Параметр radius окружности установлен в половину значения topHeight. Благодаря этому окружность отлично вписывается в имеющееся пространство.

Теперь давайте взглянем на координаты кривых.

• Координаты (x0, y0) задают начальную опорную точку кривой. Эти координаты всё время остаются постоянными. Координата x0 представляет собой центр диаграммы (половина size), а y0 — это координата, в которой заканчивается нижняя часть окружности. Поэтому в формуле расчёта этой координаты используется радиус окружности. В результате координаты этой точки можно найти по следующей формуле: (50% size, 20% size + radius).
• Координаты (x1, y1) — это первая управляющая точка кривой. Она тоже остаётся неизменной для всех кривых. Если не забывать о том, что кривые должны быть симметричными, то оказывается, что значения x1 и y1 всегда равняются половине значения size. Отсюда и формула для их расчёта: (50% size, 50% size).
• Координаты (x2, y2) представляют вторую управляющую точку кривой Безье. Здесь показатель x2 указывает на то, какой формы должна быть кривая. Этот показатель вычисляется для каждой кривой динамически. А показатель y2, как и ранее, будет представлять собой половину от size. Отсюда и следующая формула для расчёта этих координат: (x2, 50% size).
• Координаты (x3, y3) — это конечная опорная точка кривой. Эта координата указывает на то место, где нужно завершить рисование линии. Здесь значение x3, как и x2, вычисляется динамически. А y3 принимает значение, равное 80% от size. В результате получаем следующую формулу: (x3, 80% size).

Перепишем, в общем виде, код элемента <path> с учётом формул, которые мы только что вывели. Процентные значения, использованные выше, представлены здесь результатами их деления на 100.

<path d="M size*0.5, (size*0.2) + radius  
         C size*0.5,  size*0.5
           x2,        size*0.5
           x3,        size*0.8"
>

Обратите внимание на то, что на первый взгляд использование процентных значений в наших формулах может показаться чем-то необязательным, опирающимся лишь на моё собственное мнение. Однако эти значения применяются не из прихоти, а из-за того, что их использование помогает добиться симметричности и правильных пропорций диаграммы. После того, как вы прочувствуете их роль в построении диаграммы, вы можете попробовать собственные процентные значения и исследовать результаты, получаемые при их применении.

Теперь поговорим о том, как мы будем искать координаты x2 и x3. Именно они позволяют динамически создавать множество кривых, основываясь на индексе (index) элементов в соответствующем массиве.

Разделение доступного горизонтального пространства диаграммы на равные части основывается на количестве элементов в массиве. В результате каждая часть получает одно и то же пространство по оси x.

Формула, которую мы выведем, должна впоследствии работать с любым количеством элементов. Но здесь мы будем экспериментировать с массивом, содержащим 5 элементов: [0,1,2,3,4]. Визуализация подобного массива означает, что необходимо нарисовать 5 кривых.

▍Нахождение динамических координат (x2 и x3)

Сначала я разделила size на число элементов, то есть — на длину массива. Эту переменную я назвала distance. Она представляет собой расстояние между двумя элементами.

distance = size/arrayLength
// distance = 1000/5 = 200

Затем я обошла массив и умножила индекс каждого из его элементов (index) на distance. Для простоты изложения я называю просто x и параметр x2, и параметр x3.

// значение x2 и x3
x = index * distance

Если применить полученные значения при построении диаграммы, то есть — использовать вычисленное выше значение x и для x2, и для x3, выглядеть она будет немного странно.


Диаграмма получилась несимметричной

Как видите, элементы расположены в той области, где они и должны быть, но диаграмма получилась несимметричной. Такое ощущение, что в её левой части больше элементов, чем в правой.

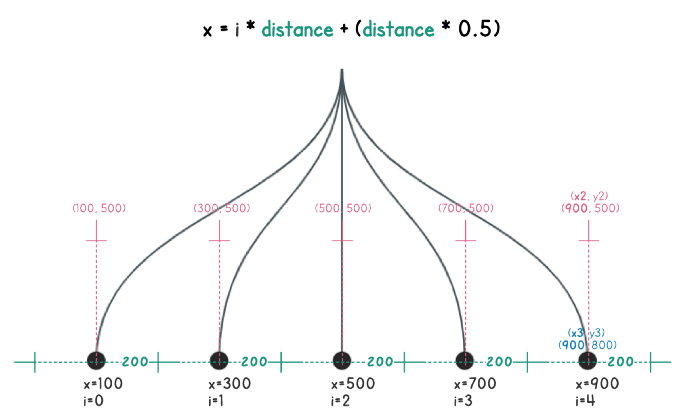
Теперь мне нужно сделать так, чтобы значение x3 оказалось бы лежащим по центру соответствующих отрезков, длина которых задана с помощью переменной distance.

Для того чтобы привести диаграмму к нужному мне виду, я просто добавила к x половину значения distance.

x = index * distance + (distance * 0.5)

В результате я нашла центр отрезка длиной distance и поместила в него координату x3. Кроме того, я привела к нужному нам виду координату x2 для кривой №2.


Симметричная диаграмма

Добавление половины значения distance к координатам x2 и x3 привело к тому, что формула вычисления этих координат подходит для визуализации массивов, содержащих чётное и нечётное количество элементов.

▍Маскировка изображения

Нам нужно, чтобы в верхней части диаграммы, в пределах окружности, выводилось бы некое изображение. Для решения этой задачи я создала обтравочную маску, содержащую окружность.

<defs>
  <mask id="svg-mask">
     <circle :r="radius" 
             :cx="halfSize" 
             :cy="topHeight" 
             fill="white"/>
  </mask>
</defs>

Затем, используя для вывода изображения тег <image> элемента <svg>, я связала изображение с элементом <mask>, созданным выше, используя атрибут mask элемента <image>.

<image mask="url(#svg-mask)" 
      :x="(halfSize-radius)" 
      :y="(topHeight-radius)"
...

> 
</image>

Так как мы пытаемся уместить квадратное изображение в круглое «окно», я настроила позицию элемента, вычтя из соответствующих показателей параметр окружности radius. В результате изображение оказывается видимым через маску, выполненную в виде окружности.

Давайте соберём всё то, о чём мы говорили, на одном рисунке. Это поможет нам увидеть общую картину хода работы.


Данные, используемые при вычислении параметров диаграммы

Создание динамического SVG-изображения с использованием Vue.js

К этому моменту мы разобрались с кубическими кривыми Безье и выполнили вычисления, необходимые для формирования диаграммы. В результате теперь мы можем создавать статические SVG-диаграммы. Если же мы объединим возможности SVG и Vue.js, то сможем создавать диаграммы, управляемые данными. Статические диаграммы станут динамическими.

В этом разделе мы переработаем SVG-диаграмму, представив её в виде набора Vue-компонентов. Также мы привяжем SVG-атрибуты к вычисляемым свойствам и сделаем так, чтобы диаграмма реагировала бы на изменение данных.

Кроме того, в конце работы над проектом мы создадим компонент, представляющий собой конфигурационную панель. Этот компонент будет использоваться для ввода данных, которые будут передаваться диаграмме.

▍Привязка данных к параметрам viewBox

Начнём с настройки системы координат. Не сделав этого, мы не сможем рисовать SVG-изображения. Вычисляемое свойство viewbox будет возвращать то, что нам нужно, используя переменную size. Здесь будет четыре значения, разделённых пробелами. Всё это станет значением атрибута viewBox элемента <svg>.

viewbox() 
{
   return "0 0 " + this.size + " " + this.size;
}

В SVG имя атрибута viewBox уже записано с использованием верблюжьего стиля.

<svg viewBox="0 0 1000 1000">
</svg>

Поэтому для того, чтобы правильно привязать этот атрибут к вычисляемому свойству, я записала имя атрибута в кебаб-стиле и поставила после него модификатор .camel. При таком подходе удаётся «обмануть» HTML и правильно осуществить привязку атрибута.

<svg :view-box.camel="viewbox">
   ...

</svg>

Теперь при изменении size диаграмма перенастраивается самостоятельно. Нам при этом не нужно вручную менять разметку.

▍Вычисление параметров кривых

Так как большинство значений, необходимых для построения кривых, вычисляется на основе единственной переменной (size), я воспользовалась для нахождения всех неизменных координат вычисляемыми свойствами. То, что мы тут называем «неизменными координатами», вычисляется на основе size, а уже после этого не меняется и не зависит от того, сколько именно кривых будет включать в себя диаграмма.

Если же size изменить — «неизменные координаты» будут пересчитаны. После этого они, до следующего изменения size, меняться не будут. Учитывая вышесказанное — вот пять значений, которые нужны нам для рисования кривых Безье:

• topHeight — size * 0.2
• bottomHeight — size * 0.8
• width — size
• halfSize — size * 0.5
• distance — size/arrayLength

Сейчас у нас осталось лишь два неизвестных значения — x2 и x3. Формулу для их вычисления мы уже вывели:

x = index * distance + (distance * 0.5)

Для нахождения конкретных значений нам нужно подставлять в эту формулу индексы элементов массива.

Теперь давайте зададимся вопросом о том, подойдёт ли нам вычисляемое свойство для нахождения x. Если коротко ответить на этот вопрос, то — нет, не подойдёт.

Вычисляемому свойству нельзя передавать параметры. Дело в том, что это — свойство, а не функция. Кроме того, необходимость использования параметра для вычисления чего-либо означает отсутствие ощутимого преимущества от использования вычисляемых свойств в плане кэширования.

Обратите внимание на то, что существует и исключение, касающееся вышеозвученного принципа. Речь идёт о Vuex. Если пользоваться геттерами Vuex, возвращающими функции, то им можно передавать параметры.

В данном случае Vuex мы не используем. Но даже при таком раскладе у нас есть пара способов решения этой задачи.

▍Вариант №1

Можно объявить функцию, которой index передаётся в качестве аргумента, и которая возвращает нужный нам результат. Этот подход выглядит чище в том случае, если мы собираемся использовать значение, возвращаемое подобной функцией, в нескольких местах шаблона.

<g v-for="(item, i) in itemArray">
  <path :d="'M' + halfSize + ','         + (topHeight+r) +' '+
            'C' + halfSize + ','         + halfSize +' '+    
                  calculateXPos(i) + ',' + halfSize +' '+ 
                  calculateXPos(i) + ',' + bottomHeight" 
  />
</g>

Метод calculateXPos() будет выполнять вычисления при каждом его вызове. Этот метод принимает в качестве аргумента индекс элемента — i.

<script>
  methods: {
    calculateXPos (i)
    {
      return distance * i + (distance * 0.5)
    }
  }
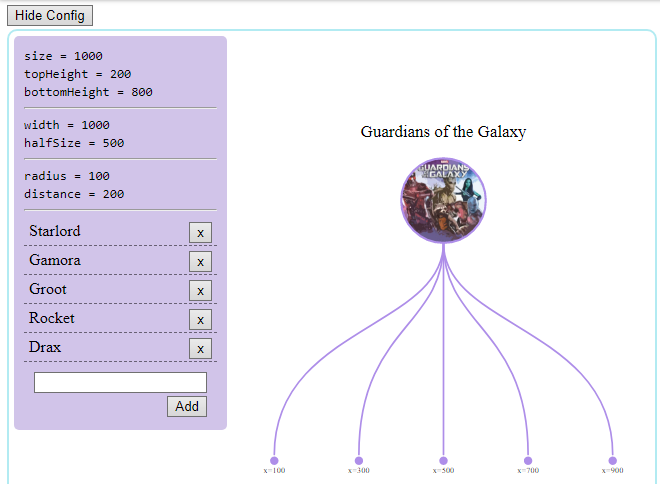
</script>

Вот пример на CodePen, в котором используется это решение.


Экран первого варианта приложения

▍Вариант №2

Этот вариант лучше первого. Мы можем извлечь маленькую SVG-разметку, необходимую для построения кривой, в отдельный небольшой дочерний компонент, и передать ему, в качестве одного из свойств, index.

При таком подходе можно даже использовать вычисляемое свойство для нахождения x2 и x3.

<g v-for="(item, i) in items"> 
    <cubic-bezier  :index="i" 
                   :half-size="halfSize" 
                   :top-height="topHeight" 
                   :bottom-height="bottomHeight" 
                   :r="radius"
                   :d="distance"
     >
     </cubic-bezier>
</g>

Этот вариант даёт нам возможность лучше организовать код. Например, мы можем создать ещё один дочерний компонент для маски:

<clip-mask :title="title"
           :half-size="halfSize" 
           :top-height="topHeight"                     
           :r="radius"> 
</clip-mask>

▍Конфигурационная панель

Конфигурационная панель

Вы, вероятно, уже видели конфигурационную панель, вызываемую кнопкой, расположенной в верхнем левом углу экрана вышеприведённого примера. Эта панель облегчает добавление элементов в массив и их удаление из него. Следуя идеям, рассмотренным в разделе «Вариант№2», я создала и дочерний компонент для конфигурационной панели. Благодаря этому компонент верхнего уровня оказывается чистым и хорошо читаемым. В результате наше маленькое приятное дерево Vue-компонентов выглядит примерно так, как показано ниже.


Дерево компонентов проекта

Хотите взглянуть на код, реализующий этот вариант проекта? Если так — загляните сюда.


Экран второго варианта приложения

Репозиторий проекта

Вот GitHub-репозиторий проекта (тут реализован «Вариант №2»). Полагаю, вам полезно будет взглянуть на него перед тем, как вы перейдёте к следующему разделу.

Домашнее задание

Попробуйте создать такую же диаграмму, которую мы здесь описали, но сделайте её ориентированной вертикально. Воспользуйтесь при этом идеями, изложенными в этом материале.

Если вы думаете, что это лёгкое задание, что для построения подобной диаграммы достаточно поменять местами координаты x и y, то вы правы. Учитывая то, что рассмотренный здесь проект не создавался как универсальный, вам, после изменения координат там, где это нужно, понадобится ещё и отредактировать код, переименовав некоторые переменные и методы.

Благодаря Vue.js наша простая диаграмма может быть оснащена дополнительными возможностями. Например — следующими:

• Можно создать механизм, позволяющий переключаться между горизонтальным и вертикальным режимами диаграммы.
• Кривые можно попытаться анимировать. Например — с помощью GSAP.
• Можно настраивать свойства кривых (скажем — цвет и ширину линии) из конфигурационной панели.
• Можно воспользоваться внешней библиотекой для организации сохранения диаграмм в каком-нибудь графическом формате или в виде PDF-файла. Эти материалы можно позволить скачивать тому, кто работает с диаграммой.

Попробуйте выполнить это домашнее задание. А если у вас возникнут проблемы — ниже будет дана ссылка на его решение.

Итоги

Элемент <path> — это одна из мощных возможностей SVG. Этот элемент позволяет с высокой точностью создавать различные изображения. Здесь мы разобрались с тем, как устроены кривые Безье, и с тем, как применять их на практике для создания собственных диаграмм.

Статические проекты обычно нелегко превращать в динамические, используя средства, предлагаемые современными JavaScript-фреймворками. Благодаря Vue.js подобные вещи делаются гораздо легче. Кроме того, надо отметить то, что этот фреймворк берёт на себя решение рутинных задач, таких, как работа с DOM. Это позволяет программисту сосредоточиться на работе с данными, причём — даже при разработке проектов с сильной визуальной составляющей.

Диаграмма, которую мы здесь создали, может казаться сложной, но мы, на самом деле, воспользовались лишь несколькими базовыми средствами Vue.js и SVG. Если вам всё это интересно — взгляните на данный материал, посвящённый разработке интерактивной инфографики средствами Vue.js. А вот — решение домашнего задания.

Надеюсь на то, что вы узнали из этой статьи что-то полезное, и на то, что вам так же интересно было её читать, как мне — писать.

Уважаемые читатели! Справились ли вы с домашним заданием?